基于免疫多输出支持向量回归算法的隧道工程位移反分析新方法
宋 威,刘开云,梁军平,徐 冲
(1.北京交通大学 土木建筑工程学院, 北京 100044;2.清华大学 环境学院, 北京 100084;3.中铁第一勘察设计院集团有限公司, 陕西 西安 710043)
隧道围岩位移的空间分布及随时间的演化能够表征围岩的变形规律,在隧道工程的建设中,隧道位移的监控量测具有十分重要的意义,可以利用隧道位移值的绝对大小及其变化速度对隧道围岩稳定程度进行判断,而通过数值模拟的方法,能够对隧道的变形过程进行模拟复现,供设计施工参考。而数值模型中参数的取值决定了数值模拟的精度,由于岩土体自身的物理力学性质复杂,受力变形过程具有高度非线性,所以准确识别岩土体的物理力学参数显得十分重要。相较于通过经验或工程类比的方法来确定参数,位移反分析方法提供了一种科学的、可控的参数取值方法,在岩土工程中得到了广泛应用[1-3]。为解决正法反分析的计算效率问题,引入智能机器学习算法来对岩体复杂非线性系统进行建模,以代替数值计算,对反分析问题进行建模求解[4-7]。人工神经网络和单输出支持向量机作为位移预测方法,被广泛地采用,取得了良好的效果。
位移反分析中的数值直接解法的精度取决于正向位移预测模型的精度和优化算法的问题寻优能力,关于机器学习模型,之前大多数研究采用的支持向量回归模型均为一维输出,只能满足单变量的预测,对于隧道变形而言,一般在同一断面监测得到的位移变量包括水平收敛和拱顶下沉,如果采用一维输出SVR算法,就需要建立两个单输出的模型,在反分析过程中将水平收敛和拱顶沉降分开考虑,但这两个变量实际上都是同一非线性系统的观测值,两者之间可能存在相互关系,而一维输出SVR模型无法考虑这种相互之间的非独立关系[8-9],本文引入一种针对多输出系统(Multiple Output System)改进的支持向量回归算法[10](MSVR),能够在同一个模型中考虑多个输出,建立统一的优化目标,进行模型训练。引入该方法考虑水平收敛和拱顶沉降的相互关系,建立统一的反演目标。关于优化算法,近年来,许多优秀的集群智能优化算法被用来对反分析中的优化问题进行求解,而人工免疫算法是模仿人体免疫机制提出的一种新的智能方法,并在近几十年来被广泛的应用于非线性优化、组合优化、控制工程、机器人、故障诊断、图像处理等诸多领域,并取得了一些成就[11-13],本文采用免疫克隆选择算法(Immune Clone Select Algorithm, ICSA),对MSVR模型控制参数进行优化,使其对样本的误差最小,将其应用于隧道位移反分析中,结合铜黄高速公路三口隧道工程进行位移反分析,验证该方法在岩土工程反分析领域的应用效果。
1 多维输出支持向量回归
1.1 一维输出支持向量回归
支持向量机学习方法是由Vapnik等[14]根据统计学的理论提出的。
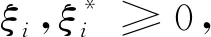
(1)
式中:w为拟合系数;ξi,ξi*为松弛因子;C为惩罚系数;k为样本数量。
约束条件为
(2)
式中:xi为第i个样本输入值;yi为第i个样本输出值;f为预测函数;ε为损失计算阈值。
对这一凸二次优化问题,采用Lagrange乘子法求解,Lagrange函数表达式为
L(w,b,ξi,ξi*,αi,αi*,γi,γi*)=
(3)

根据KKT条件,其对偶形式最大化函数表达式为
(4)
式中:xi为第i个样本输入值;xj为第j个样本输入值。
约束条件为
(5)
求解优化问题得到支持向量回归模型,表达式为
(6)
式中:x为需要预测的样本输入值。
上述分析适用于线性回归问题,对于非线性回归,需要引入特征空间,使用一个非线性映射把数据映射到一个高维特征空间进行线性回归,在高维特征空间用核函数来代替线性回归中的内积运算,核函数的定义为
K(xi,xj)=φ(xi)·φ(xj)
(7)
式中:φ为非线性映射函数。
经过与线性回归相同的推导,最后得到的支持向量模型拟合函数为
(8)
核函数种类较多,径向基函数核函数(Radical Basic Function,RBF)是一种常用的效果较好的核函数,表达式为
(9)
式中:x,y为两样本输入值;σ为核函数参数。
1.2 多维输出支持向量回归
传统的支持向量回归的输出变量为一维变量,该特点使其应用场景受到限制,在一些复杂的系统里,需要建立多输入-多输出的映射系统,而一维SVR并不能完成此类任务,因此,文献[10]在一维SVR的基础上进行扩展,使其适用于多维输出系统,以解决实际工程中更为复杂的问题。
将一维ε不敏感损失函数扩展到多维,定义损失函数,表达式为
(10)
基于式(10)所示损失函数,构造优化目标函数,表达式为
(11)
为解决MSVR模型的数学优化问题,文献[10]中提出了采用迭代加权最小二乘法(Iterative Reweighted Least Squares)来求解。
在式(11)的优化目标函数中,将损失函数用一阶泰勒展开来近似替代,即
(12)

构造式(12)的二次近似代替,文献[10]中采用的近似公式为
(13)
式中:CT为不依赖于W和b的常数项。
采用近似公式(13)的原因是该公式中W和b解耦合,优化求解不需迭代,直接取对W和b的偏导数等于0即可计算出W和b的近似解。
算法流程如下:

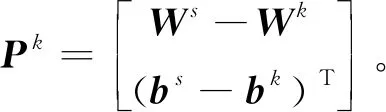
Step3计算下一迭代步的解,迭代计算公式为
(14)
式中:ηk为迭代步长。
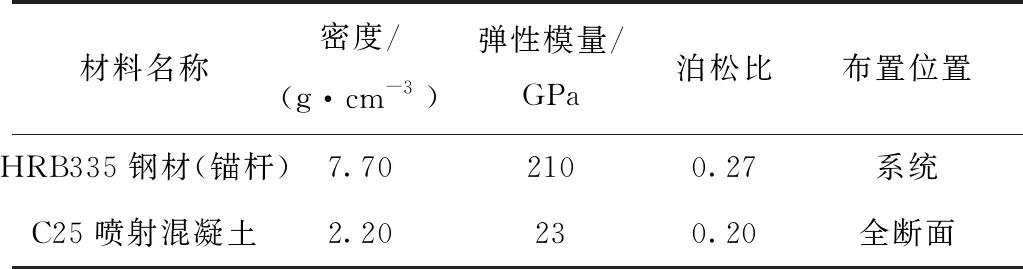
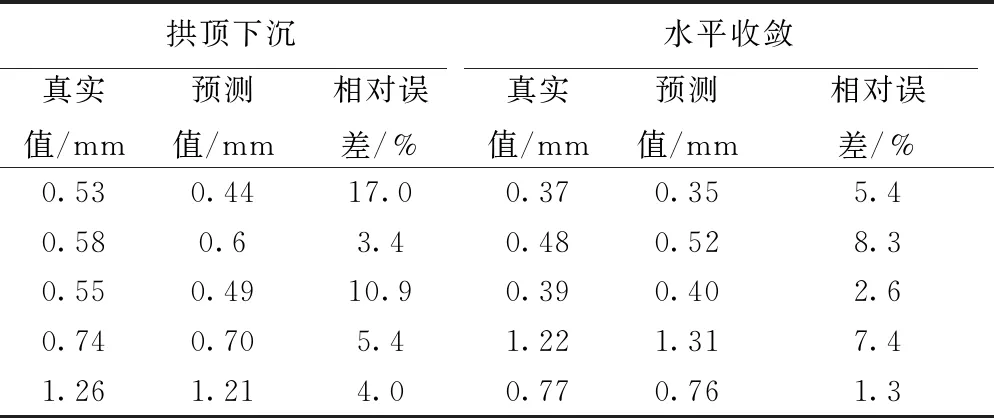
采用回溯算法来确定迭代步长。每个迭代步的初始步长设置为1(初始步长的选取对于算法的收敛非常重要),然后检查LP(Wk+1,bk+1) Step4计算uik+1和αi,设置k=k+1,回到Step2,直到满足收敛条件,达到收敛。 优化目标求解完毕得到使样本集合总体损失最小的W和b,多输出支持向量回归模型即建立完毕,多输出支持向量回归称为MSVR。 生物免疫系统是一个复杂的自适应系统。人体免疫系统能够识别病原体并做出应答反应,从而具有一定的学习、记忆和模式识别的能力。可以将其信息处理的原理、机制采用计算机算法进行描述,来解决科学和工程问题。Castro[15]最早提出了克隆选择算法 (ICSA),该算法是受人体免疫系统启发,模拟生物免疫系统功能和作用机理对复杂问题进行求解的智能方法,它保留了生物免疫系统所具有的若干特点,包括全局搜索能力;多样性保持机制;鲁棒性强;并行的求解搜索过程。将其引入对优化问题进行求解。 在ICSA算法中加入了种群抑制过程,来对种群的平均浓度进行控制,避免算法过早的收敛到局部最优解,增加全局优化能力。ICSA算法的详细过程见图1。 图1 ICSA算法流程图 采用典型多峰函数Rosenbrock函数(香蕉函数)检验改进后的ICSA算法的优化能力,其函数表达式为 (15) 式中:X=[x1,x2,…,xn]∈RN Rosenbrock函数全局最小值点在所有自变量取值为1时取得,函数值为0。用10元Rosenbrock函数检验ICSA算法对于多元函数的优化效果。自变量的搜索区间为(-10,10),算法参数设置见表1。 表1 优化算法控制参数取值 运行10次优化算法,大约4次找到函数的最小值点,这10次的优化结果见表2。由表2可知,ICSA算法具有良好的多维多峰值函数的寻优能力,可以应用于求解MSVR模型的优化问题以及基于ICSA-MSVR耦合算法的岩体物理力学参数位移反分析。 表2 Rosenbrock函数优化结果 MSVR模型的建立过程中,控制参数(惩罚系数C,敏感系数ε,核函数参数σ)的取值需要人为指定,为了控制参数取值来达到最小的样本训练误差及最好的MSVR模型泛化精度,采用ICSA算法对参数进行优化求解。 在模型训练阶段,定义训练样本集合的总体误差函数为优化目标,单个样本的误差同样采用ε不敏感损失函数,见式(10),将训练样本分为学习样本和测试样本,采用K折交叉验证的方法来计算样本整体误差,优化目标函数表达式为 (16) 式中:Lall(C,ε,σ)表示整体的训练损失函数;k表示样本等分的份数;km表示训练样本k等份后每份的数量;上标星号表示求得的最优参数。 待MSVR模型训练完毕,即通过ICSA算法优化求得最优的MSVR模型参数后,即完成正法反分析过程中的位移预测模型的建立过程。 MSVR模型建立完成后,可以进行岩体的物理力学参数辨识过程。 给定待反演岩体物理力学参数的取值范围,优化目标函数为预测位移(拱顶沉降和水平收敛)的误差函数,其表达式为 (17) aff(x)=[fu(x)-u]2+[fv(x)-v]2 式中:x为待反演参数向量,即围岩的物理力学参数,选取的7个参数为重度、变形模量、黏聚力、内摩擦角、水平侧压力系数、泊松比、剪胀角;fu(x)为MSVR模型预测水平收敛;fv(x)为MSVR模型预测拱顶下沉;u为现场实测水平收敛;v为现场实测拱顶下沉;aff为亲和度函数(即优化目标函数,最小化问题)。 优化完成后输出优化结果,完成参数反演,得到岩体力学参数的辨识结果。 将辨识参数输入到MSVR模型中,对隧道开挖的后续位移进行预测。以验证辨识得到的参数是否符合工程实际。 ICSA-MSVR耦合算法的流程见图2,在定义误差函数和结果输出部分模型训练过程和参数辨识过程有所不同。 图2 ICSA-MSVR耦合算法流程 在ICSA算法的优化过程中,为了扩大参数的搜索范围和搜索效率,将待优化参数进行了指数映射,即在种群中的参数的取值范围是实际的取值范围的自然对数,在实际亲和度计算中,将抗体个体进行指数映射,计算公式为 P′=exp(P) (18) 式中:P为每个个体的取值(对于模型训练过程P为三个支持向量回归控制参数C,ε,σ,对于力学参数反演过程P为待反演的7个岩体的物理力学参数)。亲和度计算采用指数映射后的个体取值P′。 铜(陵)—黄(山)高速公路铜汤段三口隧道为双向分离式四车道高速公路隧道,左、右线隧道间距约为46 m,左线隧道超前右线隧道施工,超前距离约为30 m,因而可以忽略右线隧道施工对左线隧道的影响。本文考察其左线出口段。该段为Ⅲ级围岩段,里程桩标号为ZK252+270—ZK252+511段,轴向掘进总长度约为241 m。 三口隧道施工方法为爆破掘进开挖,隧道研究段为全断面一次开挖,以3 m为循环进度,每天掘进6 m。在隧道施工过程中设置监测断面,对隧道收敛和沉降变形进行监测,ZK252+510监测面测点位移见表3。 三口隧道横断面见图3,通过Midas建立网络模型,然后导入FLAC3D中进行计算,整体数值计算模型见图4。采用均质材料的假设,沿隧道轴线方向为y轴方向,垂直向上为z轴方向,x轴水平向右为正方向,模型从左至右宽为60 m;从坐标原点往下长为50 m;计算模型沿纵向长80 m,单元共42 500个,节点共43 768个。 图3 三口隧道断面(单位:m) 图4 三口隧道数值计算模型 对模型前后左右及下边界施加法向变形约束,上边界为自由边界。由于没有实测地应力资料,垂直地应力等于上覆岩层自重。两个水平方向地应力相等,等于竖向地应力乘以水平侧压力系数。 隧道初期支护采用喷锚支护,喷射混凝土采用C25混凝土,厚度10 cm,锚杆布置长度为2.5 m,环向间距1.5 m,锚杆采用全长粘接水泥砂浆锚杆,钢材为HRB335,直径为25 mm。锚杆钢材和C25喷射混凝土的本构均为弹性本构,参数见表4。锚杆数值模型见图5。 表4 隧道初期支护材料力学参数 隧道采用全断面开挖,数值模拟中循环进尺为3 m,初期支护紧跟掌子面。变形监测断面设置在距离隧道出口处1 m的位置。变形监测点见图6。 图6 变形监测点布置 参考JTG D70—2014 《公路隧道设计规范》[16],围岩物理力学指标见表5。 表5 围岩物理力学参数取值范围 我国地应力实测资料表明水平侧压力系数范围为0.55~2.00。剪胀角对计算结果的影响不大,剪胀角取值范围是3°~16.5°。采用7因素28水平的均匀试验划分,因素选择为重度、变形模量、黏聚力、内摩擦角、水平侧压力系数、泊松比、剪胀角7个因素,应用均匀试验法设计28个数值试验方案,采用 FLAC3D 软件进行三口隧道左线施工的三维数值模拟,考虑不同的掌子面与 ZK252+510 监测面的距离,从数值实验的结果中随机抽取35次数值计算结果,组成供MSVR 算法进行网络训练的 30个训练样本见表6,5个检验样本见表7。训练样本采用K折交叉验证法进行MSVR模型的学习及建立。表7所示的检验样本完全不参与MSVR模型的训练过程,只用来检验训练得到的MSVR模型的泛化性能。MSVR采用径向基核函数,并对样本进行归一化处理,将数据线性映射到[0,1]。将拱顶下沉和水平收敛作为MSVR模型的输出变量建立MSVR模型,对模型参数(C,ε,σ)进行优化。三个参数的搜索区间依次为(0,10 000)、(0,100)、(0,10 000),经过ICSA算法优化后,MSVR模型最优参数C,ε,σ的数值分别为19.4、0.004 59、2.10。 表6 MSVR模型训练样本集 表7 检验MSVR训练效果的检验样本集 为检验模型泛化性能,对表7所示检验样本,用训练好的MSVR模型进行位移预测,结果见表8。 表8 检验样本的MSVR模型预测效果 由表8可知,MSVR模型对于拱顶下沉和水平收敛的预测精度较好,表明映射围岩物理力学参数与位移之间非线性关系的MSVR模型已经建立,可以用于岩体物理力学参数的辨识。 利用训练完成的MSVR模型,对岩体物理力学参数进行反演,7个待反演参数的反演区间见表9。将拱顶沉降和水平收敛统一反演,两者权重相等,反演目标函数见式(17),取监测面距离掌子面5 m处时的位移值作为反演基础信息。反演得到的岩体物理力学参数见表9。 表9 待反演、反演参数取值范围 利用反演得到的岩体力学参数,输入MSVR模型对后续位移(d=8、11、14 m)进行预测,预测效果见表10。由表10可知,利用ICSA-MSVR算法对隧道进行位移反分析,其后续位移预测中,拱顶下沉和水平收敛的预测具有较好的精度,误差最大在15%左右,说明基于免疫多输出支持向量回归算法的位移反分析方法具有较高的精度。 表10 反演参数预测后续位移 为进一步说明本文所述ICSA-MSVR算法对位移反分析问题的求解效果,与文献[7]中方法进行对比,文献[7]中采用遗传-广义回归神经元网络算法(GRNN)对坞石隧道进行位移反分析,基于坞石隧道的实测位移值,对隧道围岩的物理力学参数进行辨识。文献[7]采用数值试验、机器学习与人工智能相结合的智能岩土工程反分析方法,与本文具有可对比性。 根据文献[7]中表6所述的隧道实际监测位移,可以确定如式(17)所示的反演目标函数,按照本节所示工程实例的相同步骤,对坞石隧道的围岩参数进行辨识,本文方法和文献[7]方法反分析得到的围岩力学参数对比见表11。 表11 反演参数对比 将反演得到的岩土参数输入到MSVR模型,进行后续的开挖步的隧道变形的预测,对比结果见表12。由表12可知,本文ICSA-MSVR算法对隧道变形的预测精度高于单一的BP方法,与遗传-广义回归神经元网络算法(GRNN)对比,精度略有提高,本文方法对拱顶沉降和水平收敛的统一反演效果较好。也体现出多输出支持向量回归算法与免疫克隆选择算法相结合的良好的位移反分析应用前景。 表12 位移预测结果对比 本文所述算法,均编制C++程序,并借助Intel OpenMP并行算法库实现了算法的并行,提高其计算效率。算法计算时间见表13。 表13 算法花费时间表 s (1) 本文提出了改进的免疫克隆选择算法,加入了种群抑制过程来改善收敛于局部极值以及算法的早熟问题,经过算例检验,该算法对多维优化问题具有良好的求解能力,且收敛速度较快。 (2) 引入多输出的支持向量回归算法,用来解决输出变量之间的依赖性以及计算效率的问题,增强了位移反分析方法的工程应用价值。 (3) 将本文方法应用于铜黄高速公路三口隧道的位移反分析中,结果显示本文方法的参数辨识效果较好,辨识的参数较为准确,对后续位移的预测精度较好,具有一定的工程应用价值。并将本文所述ICSA-MSVR算法与遗传-广义回归神经元网络算法进行了参数辨识的对比,验证了本文方法的优势。2 免疫克隆选择算法
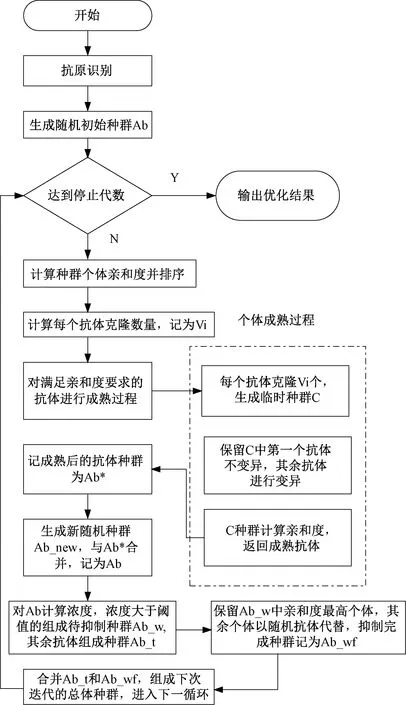


3 基于ICSA-MSVR耦合算法的岩体物理力学参数位移反分析
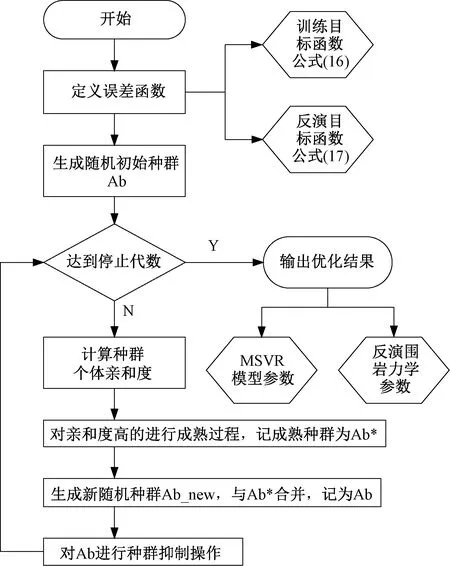
4 工程实例
4.1 三口隧道工程概况
4.2 训练样本的获取——数值试验


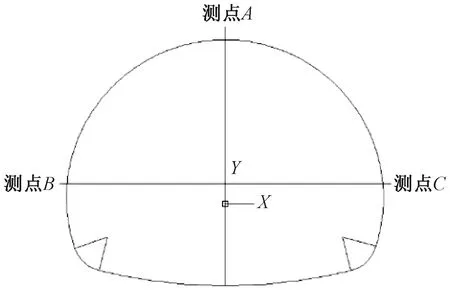

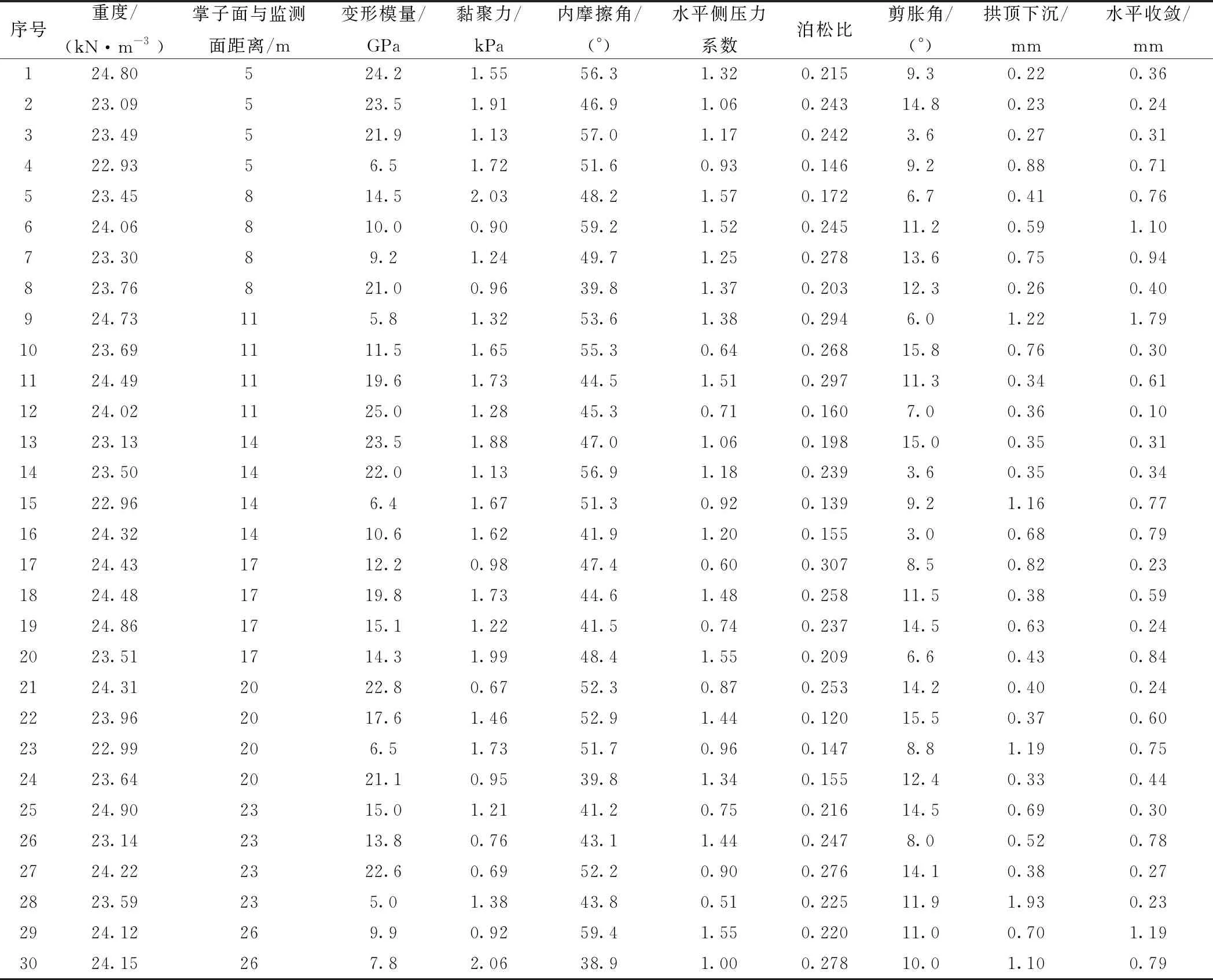

4.3 岩体参数的反演及后续位移预测





5 结论

