双块式无砟轨道枕边裂缝水力伤损特性

杨荣山，胡 猛,2，孔晓钰，康维新，曹世豪

(1.西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都 610031；2.同济大学 道路与交通工程教育部重点实验室， 上海 201804；3.河南工业大学 土木建筑学院，河南 郑州 450001)

双块式无砟轨道作为我国高速铁路无砟轨道结构的主要形式之一，因简单可靠、便于施工、建设成本低等优点在武广、郑西、兰新等高速铁路线路大规模运用。然而由于双块式无砟轨道长期承受列车动载、温度荷载、雨水侵蚀等复杂作用，其整体性能会不断劣化[1]。现场调研发现，双块式无砟轨道较为典型的伤损为轨枕周边开裂、冒浆、脱空等病害，如图1所示。特别是在强降雨或排水不良地段，其伤损情况较干燥地区更为严重。

图1 双块式无砟轨道轨枕开裂、松动

双块式轨枕与道床板的新旧混凝土界面容易产生初始裂纹，在列车荷载和温度作用下会在轨枕周边形成宏观裂缝。当轨枕周边裂缝存在积水时，在列车动荷载的作用下将加速其伤损过程，列车经过时，道床板受弯而挤压裂缝内积水，进而产生动水压力，产生的动水压力反作用于裂缝两侧表面，裂缝尖端处产生应力集中，长期作用下裂缝不断发生疲劳扩展，以致轨枕底部裂缝贯穿，造成轨枕脱空现象。水的存在对无砟轨道伤损发展起着非常关键的作用，无砟轨道裂缝处水力劈裂与混凝土、岩石等材料的水力破坏相似，国内外学者在混凝土水力破坏方面开展了大量研究，文献[2]认为裂缝内动水压力与流速满足达西定律；文献[3-4]通过理论推导动水压力与裂缝口位移关系式，认为裂缝内高频荷载产生的水压力较大；文献[5-6]的机械荷载与水压力耦合作用下的水力劈裂试验研究表明，裂缝内水压力会降低结构的承载能力；王海龙等[7]基于细观断裂力学，研究了外部荷载作用下混凝土中孔隙水压力对裂缝扩展的加速效应。然而由于水致损伤产生和发展机制的复杂性，目前针对无砟轨道裂缝内水力劈裂的研究较少，徐桂弘等[8]通过室内模型试验，研究了荷载幅值对裂缝内水压力的影响；杨荣山等[9]基于流固耦合理论，研究了列车运行速度、轴重等对动水压力分布特性的影响；洪康等[10]将列车荷载简化为正弦或冲击荷载，研究了已脱空轨枕周边裂缝内的水力特性。现有研究对无砟轨道裂缝内水压力分布特性等做了一定的论述，但计算模型较为简单，将简化的荷载形式作为边界条件分析无砟轨道裂缝内水力特性，无法较好地模拟高速列车通过时裂缝内水压力真实分布情况，也并未给出裂缝产生的原因及裂缝发展趋势，缺乏较为系统的阐述，对于无砟轨道养护维修指导意义并不大。因此，分析列车动荷载与水耦合作用下无砟轨道裂缝内动水压力分布及裂缝扩展特性非常必要。

本文以双块式无砟轨道轨枕周边裂缝为研究对象，首先基于流固耦合理论与车辆-轨道耦合动力学理论对列车动荷载作用下裂缝内水压力进行理论推导与分析，然后基于断裂力学裂缝疲劳扩展理论，对裂缝的扩展特性及疲劳寿命展开研究，研究成果有助于解释双块式无砟轨道轨枕脱空破坏的机制，确定双块式无砟轨道合理的养护维修时机。

1 双块式轨枕水力伤损计算模型及参数

随着列车的趋近与远离，双块式无砟轨道轨枕周边裂缝会周期性地张开与闭合，裂缝内的水受挤压作用产生高频动水压力，导致裂缝扩展。为了分析高速列车通过时轨枕周边裂缝的水力劈裂行为，建立如图2所示的双块式无砟轨道轨枕裂缝扩展计算模型。

图2 计算模型

计算模型由轨枕、道床板、支承层、轨枕裂缝组成，假定裂缝形状为三角形，位于轨枕与道床板交界面处且其内部充满水，列车荷载施加于轨枕上，支承层底部以等效均布弹簧模拟路基弹性基础的影响。相关计算参数见表1[11-12]。

表1 计算参数

2 计算理论

2.1 裂缝内动水压力分布解析推导

计算模型中轨枕周边裂缝区域放大图如图3所示，图中a为裂缝宽度，L为裂缝长度，C1为控制体1,C2为控制体2。

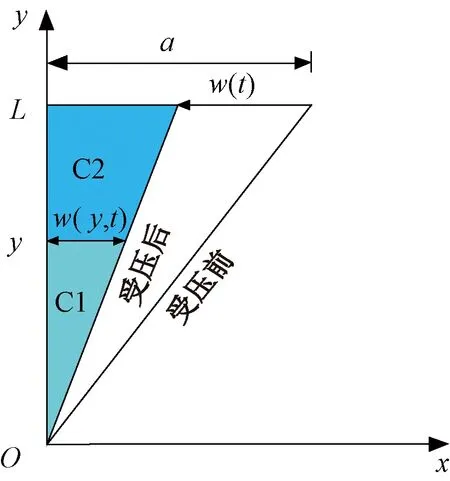
图3 裂缝放大图

对于不可压缩流体，流体力学质量守恒定律及动量定理的积分表达式为[13]

( 1 )

( 2 )

式中：ρ为水的密度,kg/m3;u为水流速矢量,m/s;F为控制体所受y方向的合力,N。

当列车经过轨枕周边开裂区时，道床板受弯，假定在钢轨支点力F(t)作用下，裂缝开口改变量为w(t)，则此时任一截面的裂缝张开量为

( 3 )

选取控制体1，假定裂缝沿线路纵向的深度为d，结合式( 1 )与式( 3 )有

( 4 )

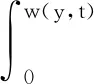
( 5 )

将式( 4 )、式( 5 )代入式( 1 )可得断面的平均流速为

( 6 )

式( 6 )为列车荷载作用下轨枕裂缝内水的断面平均流速分布解析式，然而实际内部流体的运动是极其复杂的，但由于边界壁面的限制，消除了流体之间的混掺作用，可认为边界处流体运动属层流运动，则流体在壁面处的切应力为

( 7 )

式中:λ为沿程阻力系数，对于层流问题，沿程阻力系数只与雷诺数Re成反比，其关系式为

( 8 )

式中:μ为流体黏度，Pa·s；ζ为断面特征长度，m。

选取控制体2，则水在y方向产生的切应力合力为

( 9 )

根据牛顿第三定律，控制体2在y方向的合力为

∑Fy=P(y)w(y,t)d-P(L)w(L,t)d-τtot

(10)

式中：P(y)为y截面的动水压力。

结合式( 3 )和式( 6 )有

(11)

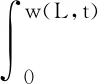
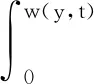
(12)

将式( 9 )、式(11)、式(12)代入式(10)后，整理可得列车动荷载与水耦合作用下轨枕周边裂缝内的动水压力解析表达式

(13)

式(13)表明在列车动载作用下，轨枕周边裂缝内水压力主要取决于两类因素的影响：裂缝几何形态、裂缝开口改变量及其变化率。

2.2 列车-双块式无砟轨道动力计算模型

为了获取高速列车经过轨枕伤损区时钢轨支点力及裂缝开口改变量的时变规律，基于车辆-轨道耦合动力学理论，采用我国高速铁路高低不平顺谱，建立车辆-双块式无砟轨道耦合垂向振动模型，将车辆视为由车体、转向架、轮对组成的多刚体系统，其中车体与转向架具有浮沉、点头两个自由度，轮对具有浮沉单个自由度，车体与转向架、转向架与车轮间一二系悬挂视为弹簧和阻尼元件，钢轨简化为均匀支承于弹性基础上的铁摩辛科梁，扣件简化为弹簧和阻尼元件，道床板与支承层采用实体单元模拟，以线性弹簧阻尼元件模拟路基弹性地基的影响，基于有限单元法求解。提取双块式无砟轨道钢轨支点力，计算模型如图4所示，其中车体参数基于我国CRH380动车组列车选取，以两车厢(8轮对)为例计算。

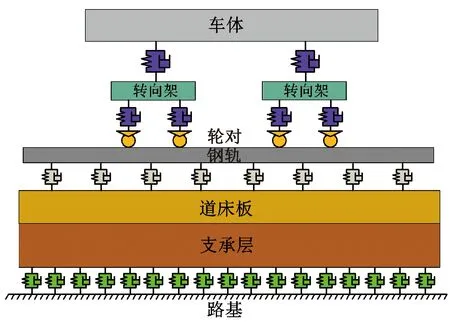
图4 车辆-双块式无砟轨道动力学垂向模型

分别以列车运行速度为250、300、350 km/h为例，计算双块式无砟轨道钢轨支点力，由于轨道各处不平顺值存在差异，因而轨道系统的动力响应在不同位置处有明显差别，故提取同一位置处的钢轨支点力，如图5所示。

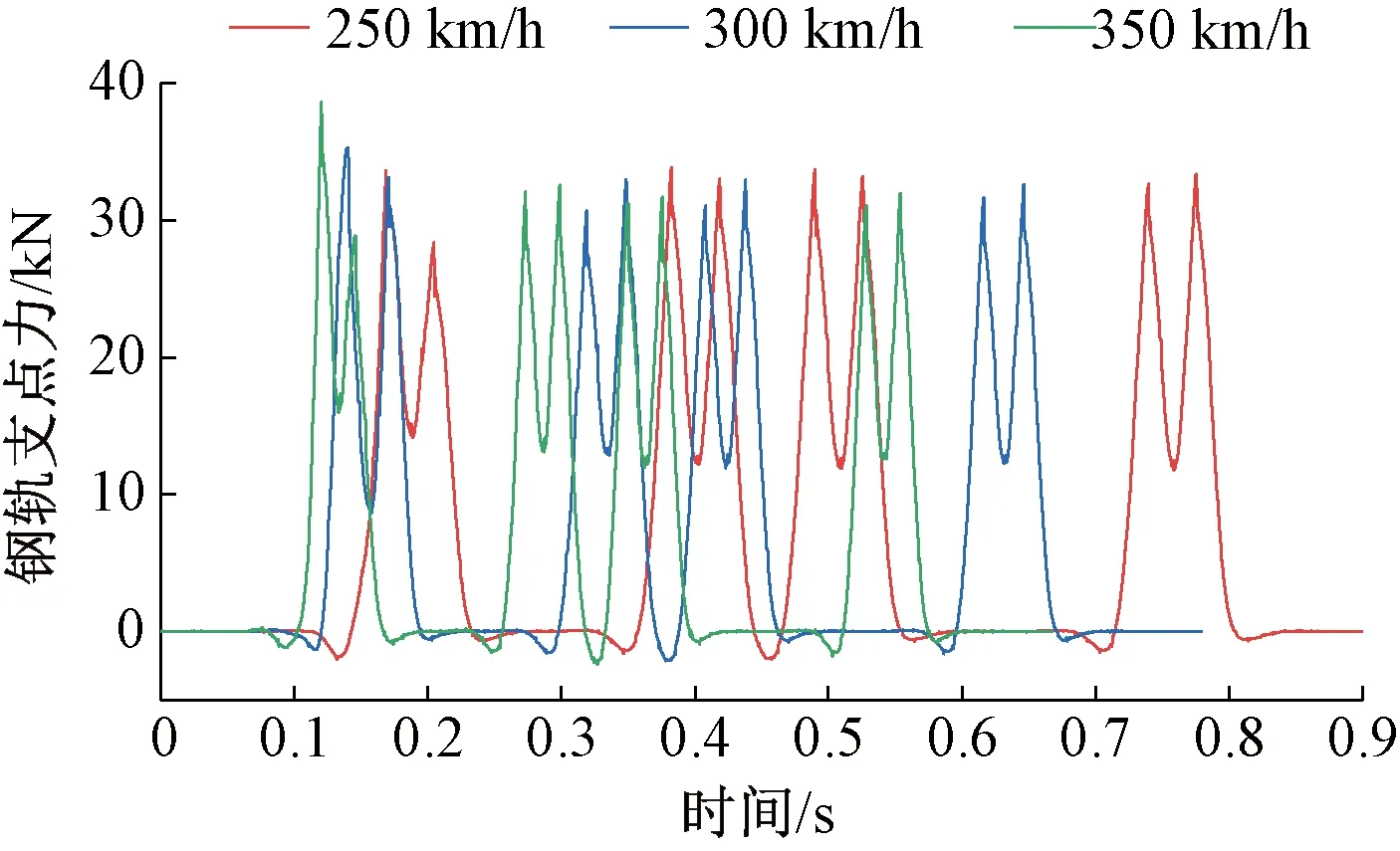
图5 钢轨支点力

裂缝开口改变量的时变规律可通过建立有限元模型并代入钢轨支点力求解，如图6所示。

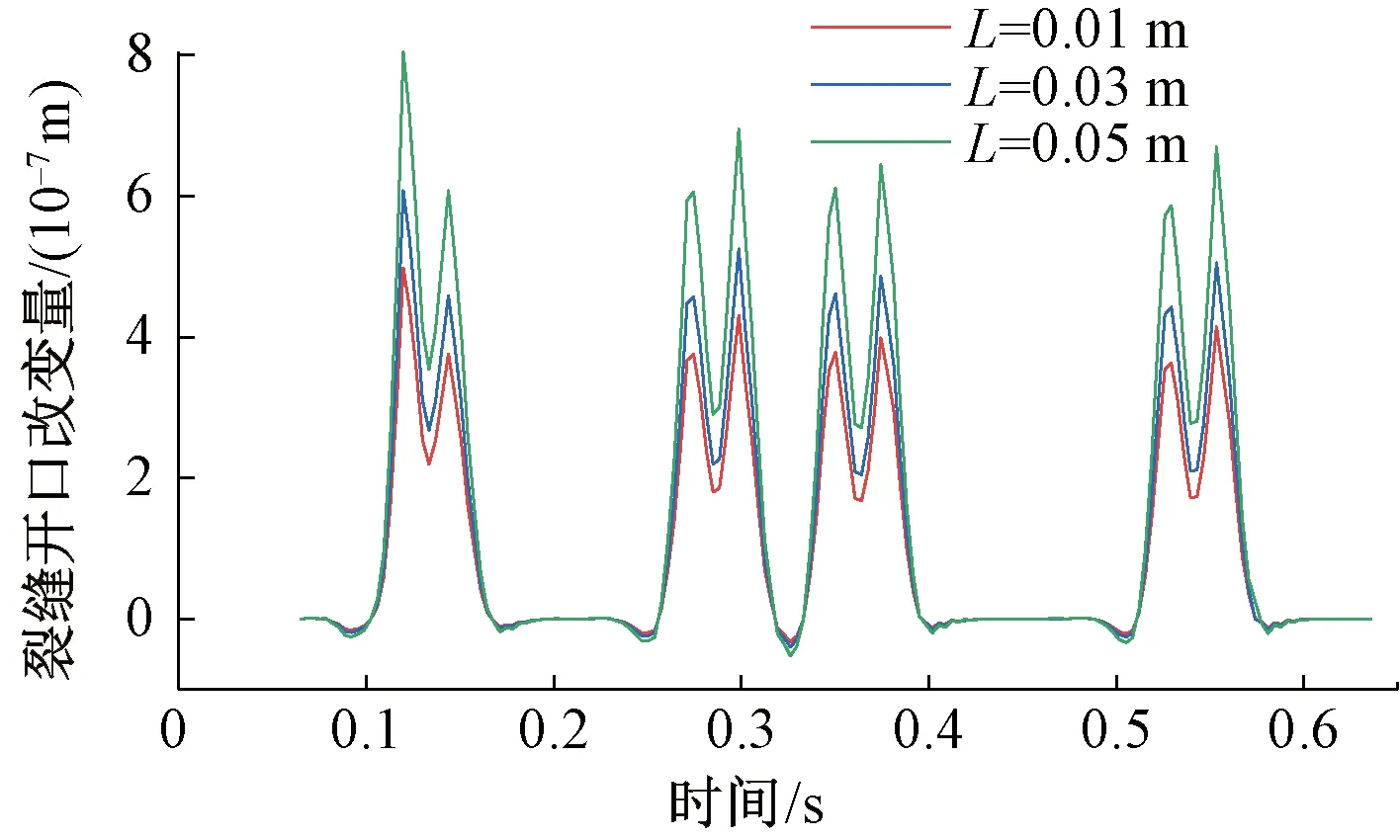
图6 裂缝开口改变量的时变规律(v=350 km/h)

2.3 轨枕周边裂缝疲劳扩展机制

一般裂纹扩展分为失稳扩展与亚临界扩展，当裂缝处于亚临界扩展状态时，若把导致扩展外因去除，则裂缝扩展很快停止。双块式无砟轨道轨枕块与道床板黏结面属新旧混凝土薄弱区问题，裂缝一般发展于此位置，由于混凝土自身因素或长期暴露在复杂环境中，轨枕周边裂缝很快达到亚临界扩展阶段，当列车趋近轨枕开裂区时，在动荷载与水的耦合作用下，裂缝张开力增大，轨枕周边裂缝尖端由于应力集中产生塑性变形，在最大剪切应力方向滑移延伸ΔL，如图7(a)到图7(b)的转变过程。裂缝尖端滑移也可能发生于另一最大剪切应力方向，如图7(c)所示。荷载继续增大，由于应变硬化，裂缝尖端向其他方向滑移，裂端形状钝化，如图7(d)所示。整个荷载上升期，裂缝共延伸ΔL。当列车远离开裂区时，裂缝张开力下降，裂端受压再度尖锐，如图7(e)所示。长期循环作用下，裂缝发生疲劳扩展，整个疲劳破坏过程如图7所示。

图7 裂缝疲劳扩展机制

应力强度因子作为裂缝扩展的驱动力，与裂缝扩展速率遵循Paris定律[14]，即

(14)

式中：ΔK为单周应力强度因子幅值差，MPa·m0.5；C、n为材料常数；N为疲劳次数。

3 列车动荷载作用下轨枕裂缝内动水压力时变与影响特性

3.1 动水压力时变特性

由于不同列车速度下轨枕周边裂缝内动水压力变化规律基本相同，故本次只选取一典型情况(列车运行速度为350 km/h，裂缝长度0.1 m，裂缝开口量大小0.2 mm)分析，基于车辆-轨道耦合动力学原理计算钢轨支点力，并运用式(13)计算轨枕周边裂缝尖端处动水压力时变曲线，计算结果如图8所示。

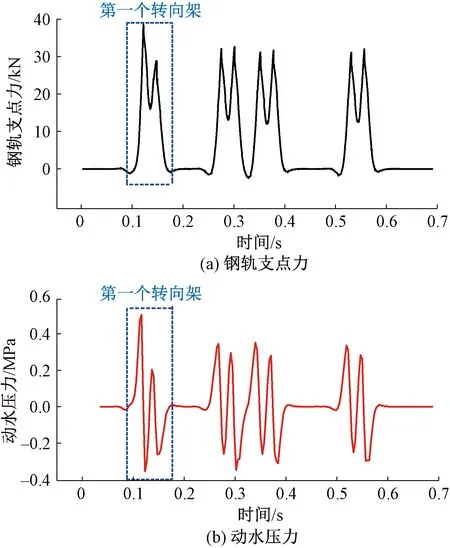
图8 钢轨支点力及动水压力时程分布

以第一个转向架为例，在如图8中虚线框线所示时间范围内进行分析，当第一轮对接近伤损区(未达到)时，动水压力呈小范围负压状态，随后动水压力急剧上升并在第一个轮对即将达到伤损区中心时达到极大值，之后动水压力急剧下降并由正压状态转变为负压状态，在转向架中心即将达到伤损区中心时，动水压力降至极小值。之后第二个轮对趋近伤损区，轨枕周边裂缝内动水压力再次上升并由负压转变为正压状态，在第二轮对临近伤损区中心时，动水压力再次达到极大值，随后动水压力再次降低并转变为负压状态，当第一个转向架驶离伤损区时，动水压力归零。第二、三、四个转向架呈现相同规律，不同的是，由于第二、三转向架距离较近，当第四个轮对驶离伤损区时，第五个轮对马上趋近伤损区，动水压力直接增长至极大值。在列车动荷载作用下，裂缝对流体的作用可归结为加速挤压、减速挤压、加速扩张、减速扩张四种情况，其中每种情况又分为w′(t)>0、w′(t)<0两个阶段。结合式(13)可知，当裂缝对流体作用位于加速挤压第一阶段时，动水压力上升呈正压状态；当裂缝对流体作用位于减速扩张第二阶段时，动水压力下降呈负压状态；当裂缝对流体作用位于其他情况时，动水压力变化情况不难通过式(13)解释。

3.2 动水压力影响特性分析

仍取上述工况(列车运行速度为350 km/h，裂缝长度0.1 m，裂缝开口量0.2 mm)分析计算，当第一轮对到达伤损区中心时，轨枕裂缝内动水压力空间分布如图9所示，由于裂缝内动水压力在裂缝尖端处呈指数型增长，故采取对数坐标。

图9 动水压力空间分布

由图9可知，动水压力沿裂缝开口方向变化较为复杂，轨枕周边裂缝内动水压力从裂缝开口处向裂缝尖端处急剧增长，裂缝尖端处动水压力达到0.5 MPa，在列车动荷载与水压力共同作用下，裂缝尖端处应力集中，裂缝面承受法向张力作用，更容易发生扩展以致轨枕处出现脱空现象。为明确动水压力极值的控制因素，比较不同列车运行速度、裂缝开口量、裂缝长度下动水压力时变特性及最大值，结果如图10所示。图10(a)代表在裂缝开口量为0.2 mm，列车运行速度为350 km/h且裂缝长度不同条件下，当第一个转向架经过伤损区时，轨枕周边裂缝尖端动水压力时变曲线，在列车动荷载与水耦合作用下，动水压力极值的绝对值随着裂缝长度的增加而显著增大。图10(b)展现了在裂缝长度一定(0.1 m)时，裂缝尖端的动水压力与裂缝开口量呈非线性变化关系，且其最大值随裂缝开口量的增大而减小，当裂缝开口量小于0.4 mm时，其变化趋势更为明显，此外，动水压力随列车运行速度的增加而增大。比较而言，动水压力对于裂缝开口量大小的改变更加敏感。

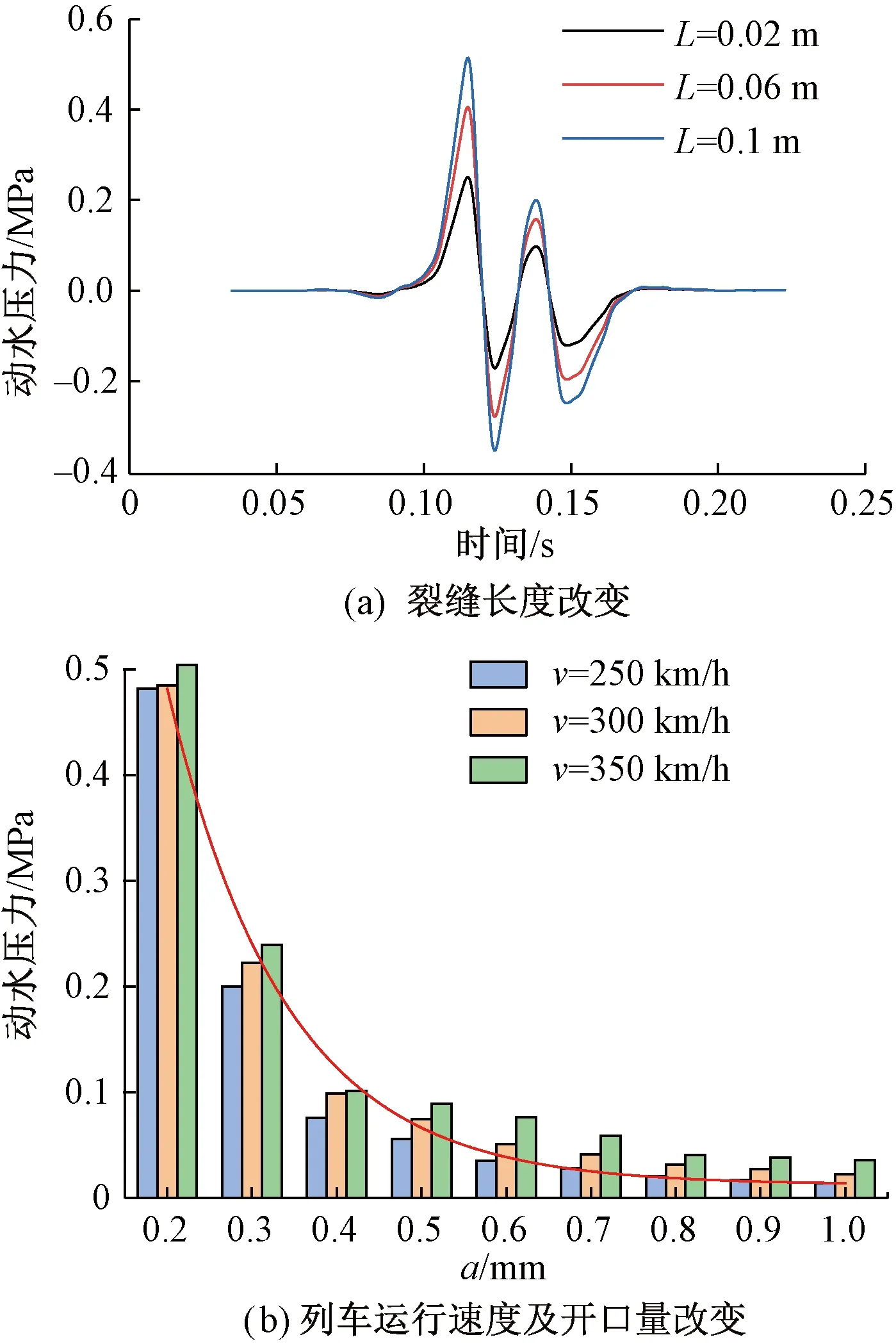
图10 不同条件下裂缝内动水压力

4 枕边裂缝扩展特性分析

4.1 裂缝尖端应力强度因子时变规律

在以图2所示模型计算得到动荷载与水耦合作用下裂缝尖端的位移场后，采用位移外推法对裂缝尖端处的Ⅰ、Ⅱ应力强度因子KⅠ、KⅡ进行计算

(15)

式中：u和ν分别为裂缝尖端前端的节点位移,m；G为材料的剪切模量，Pa；κ为弹性常数，其中κ=3-4μ(平面应变假设)；μ为泊松比；r和θ为裂缝尖端的极坐标；O(r)为高阶项。

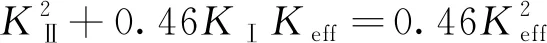
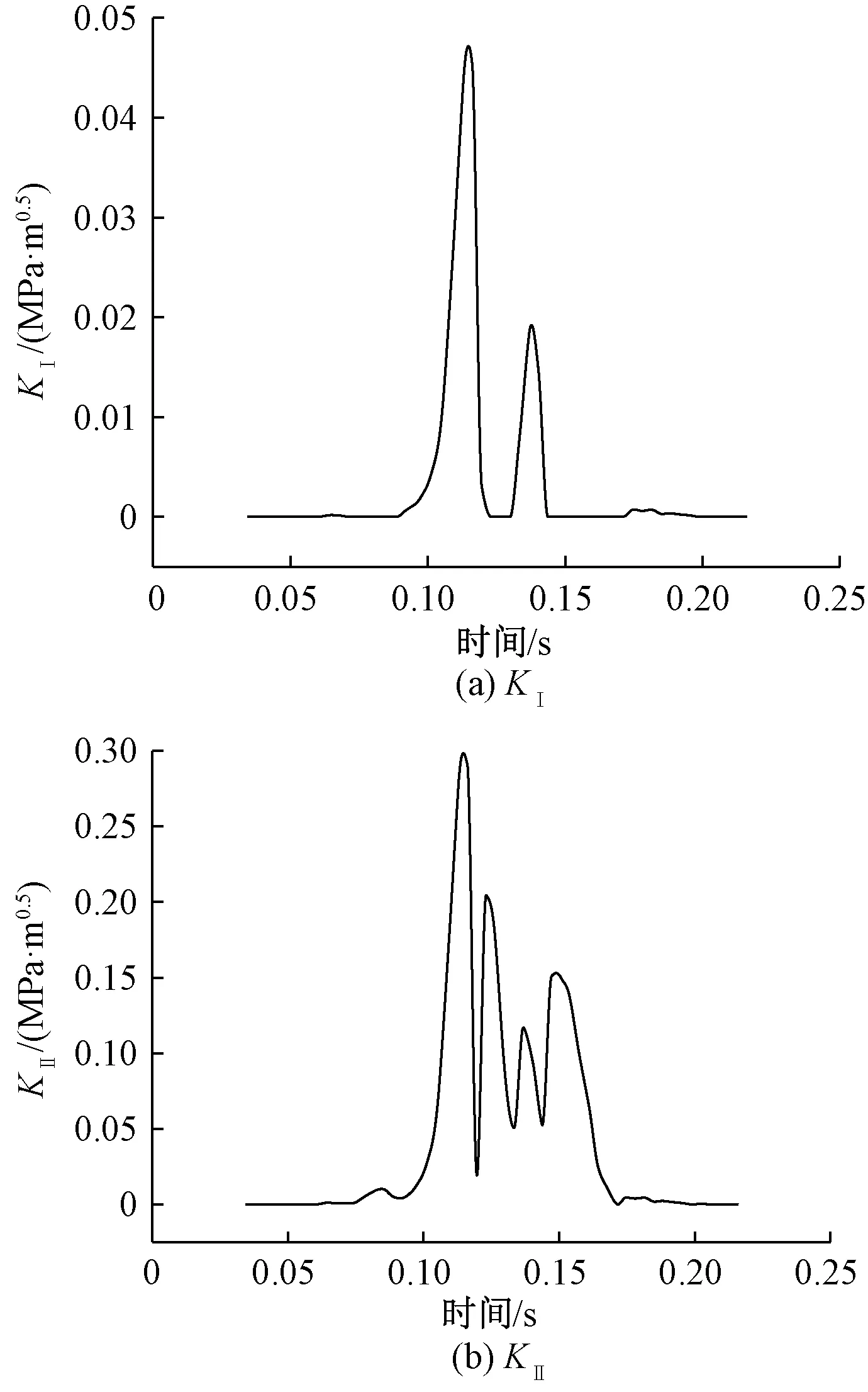
图11 应力强度因子时变特性

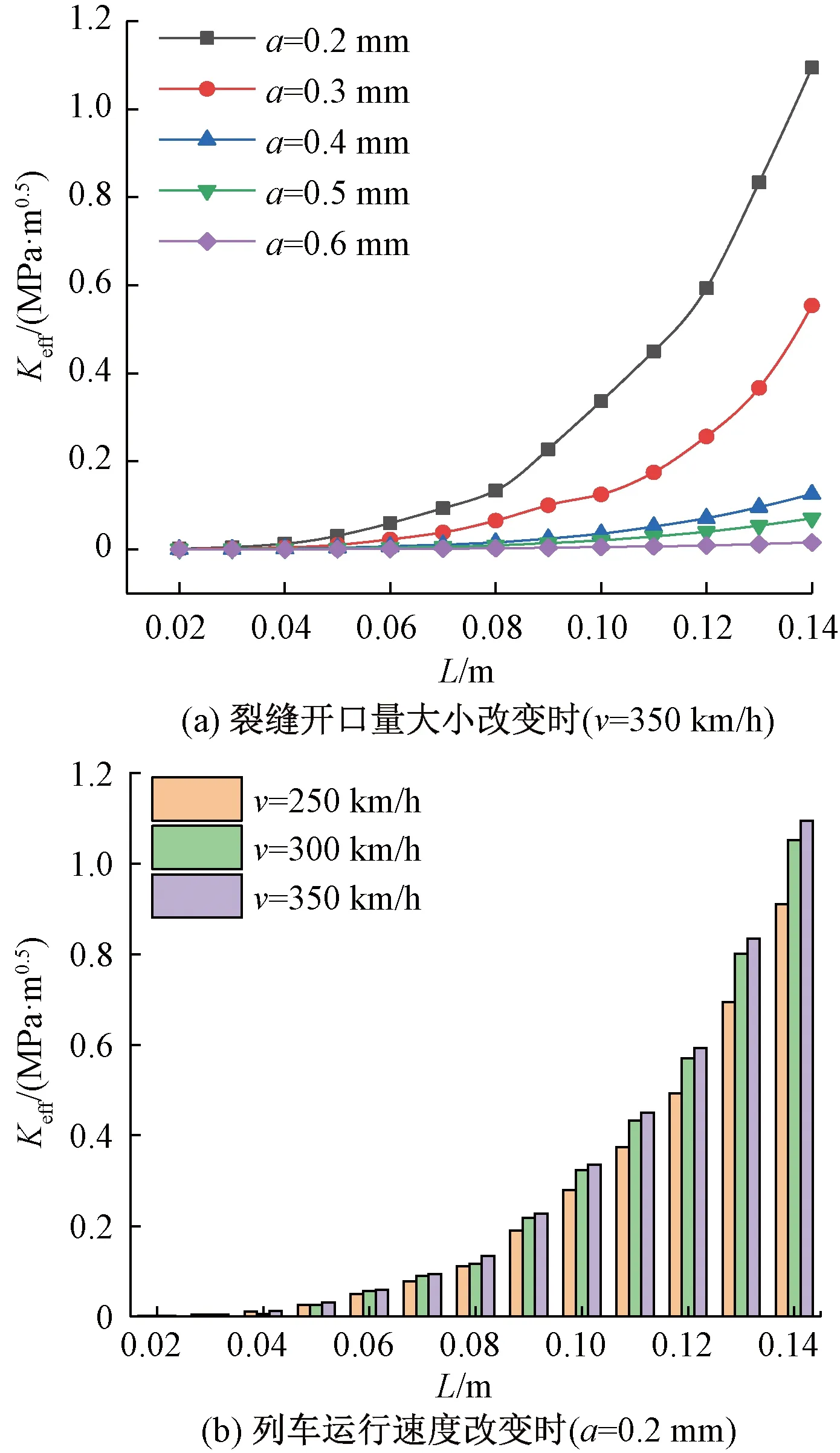
图12 等效应力强度因子最大值变化规律

图12(a)、图12(b)分别代表在列车速度不变(350 km/h)和裂缝开口量固定不变(a=0.2 mm)条件下，裂缝开口量大小、裂缝长度与列车运行速度对裂缝尖端等效应力强度因子的影响。根据图12可知，裂缝尖端处的等效应力强度因子随裂缝长度的增加而增大，此外由图12(a)可以发现，当裂缝长度固定不变时，随着裂缝开口量减小，裂缝尖端Keff明显增大，且其增加速率随开口量的减小而增大。由图12(b)可以发现，当裂缝长度固定不变时，裂缝尖端处的Keff随列车运行速度的增加而增大。

采用复合型断裂准则描述列车动荷载与水耦合作用下无砟轨道轨枕周边裂缝劈裂行为，当裂缝尖端的等效应力强度因子满足式(16)所示关系时，裂缝发生失稳扩展。

Keff≥Kun

(16)

式中:Kun为裂缝失稳断裂韧度，MPa·m0.5，对于混凝土裂缝失稳扩展临界断裂应力强度因子，参考文献[15]得到其与混凝土劈裂抗拉强度的关系，即

Kun=0.286kft

(17)

其中:ft为混凝土劈裂强度,MPa；k为结构尺寸效应系数。

基于复合型断裂准则，对不同速度列车动荷载作用下无砟轨道安全性能进行分析，结果见表2。由表2可知，在裂缝开口量为0.2 mm条件下，当列车运行速度为350 km/h时，裂缝的临界断裂长度约为0.08 m；当列车运行速度为250 km/h或300 km/h时，裂缝的临界断裂长度不超过0.09 m。在列车动荷载与水的耦合作用下，一旦裂缝长度大于其临界失稳扩展长度，轨枕周边裂缝直接沿交界面处发生失稳扩展，以致在轨枕底部产生贯通，影响行车的平稳与安全性。

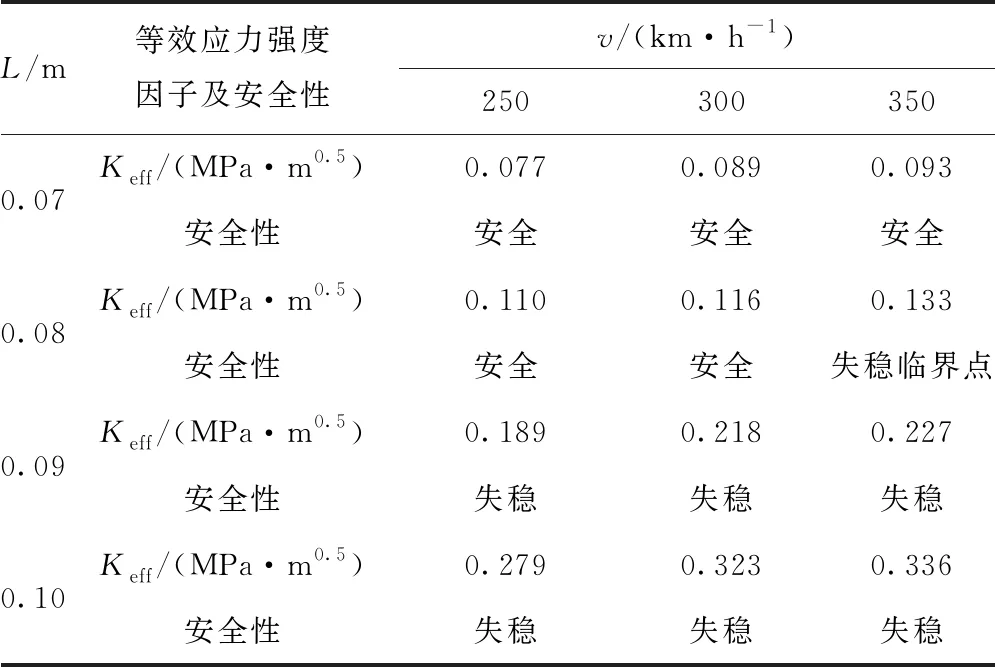
表2 不同速度列车荷载作用下无砟轨道轨枕周边裂缝安全性(a=0.2 mm)

4.2 枕边裂缝疲劳扩展特性分析

假定裂缝初始长度为Lini，裂缝失稳断裂长度为Lun，对式(14)取倒数并进行积分可得轨枕周边裂缝疲劳寿命，即

(18)

根据复合型断裂准则，对不同速度列车荷载、不同裂缝开口量下无砟轨道轨枕裂缝失稳临界断裂长度进行计算，结果见表3。

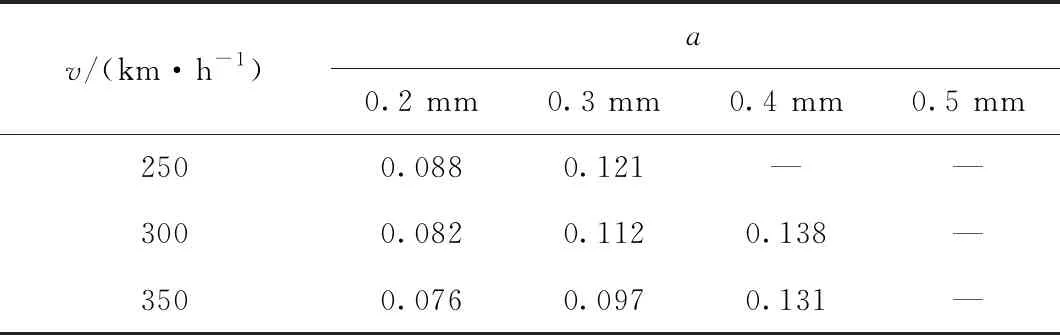
表3 枕边裂缝失稳临界断裂长度 m

由表3可知，随着列车速度的提高或裂缝开口量的减小，裂缝的临界断裂长度减小，裂缝更容易发生失稳扩展，当列车运行时速为350 km/h且裂缝开口量为0.2 mm时(裂缝失稳长度约为0.076 m)，结合式(19)计算不同裂缝初始长度下轨枕周边裂缝水力劈裂疲劳寿命，其中式(19)参数取值参考文献[16]，结果如图13(a)所示(对数坐标)。图13(a)表明，裂缝的疲劳寿命随裂缝初始长度Lini的增加急剧减小，这是由于裂缝初始长度较小时裂缝扩展速度非常缓慢所造成的，此时结构偏于安全。当裂缝初始长度从0.01 m增加到0.07 m时，裂缝扩展速度增大，此时裂缝的疲劳寿命很短，在高频动载作用下很快达到裂缝失稳临界点，造成结构破坏。由此可见，裂缝初始长度是裂缝寿命的控制性因素，对裂缝的疲劳寿命起关键性的作用，建议裂缝的失稳长度与初始长度之差大于0.05 m。

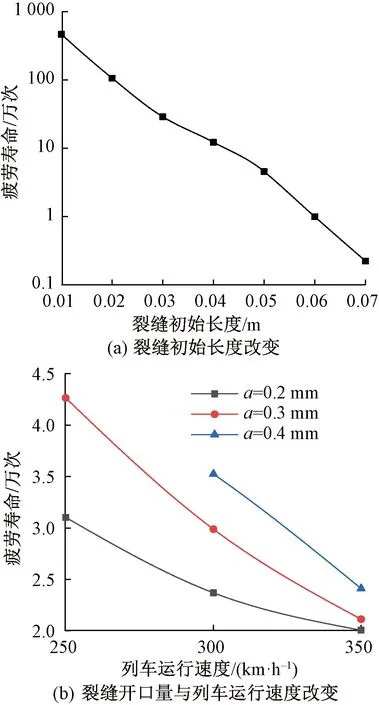
图13 不同条件下裂缝疲劳寿命

当裂缝的初始长度比其临界断裂长度小某一固定值时(本文以0.02 m为例分析，其余初始裂缝长度对应计算结果呈相同规律)，计算不同速度列车荷载及不同裂缝开口量条件下无砟轨道轨枕周边裂缝的疲劳寿命，结果如图13(b)所示。根据图13(b)，轨枕周边裂缝疲劳寿命随裂缝开口量的增加而增大，且其增大速率随列车运行速度的提高而减小。此外不难发现，列车运行速度越高，轨枕周边裂缝扩展速率增加得越迅速，相同条件下列车运行速度为350 km/h时对应轨枕裂缝的扩展速率是列车运行速度为250 km/h时对应裂缝扩展速率的1.5～2倍。综上所述，裂缝的初始长度及列车的运行速度是双块式无砟轨道轨枕裂缝疲劳寿命的关键影响因素，在列车动荷载与水的耦合作用下，枕边裂缝沿新旧混凝土交界面扩展，很快于轨枕底部产生贯通。

5 结论

本文以路基上双块式无砟轨道为例，将轨枕处裂缝形态简化为三角形，运用流固耦合及疲劳断裂理论建立了轨枕周边裂缝内动水压力及裂缝扩展计算模型，对高速列车动荷载作用下轨枕内动水压力分布特性及裂缝的扩展特性进行了分析。主要结论如下：

(1)高速列车作用下，轨枕周边裂缝内动水压力值呈正负交替状态，当轮对经过伤损区时，动水压力呈最大正压状态，当转向架中心经过伤损区时，动水压力呈最大负压状态。轨枕裂缝内动水压力分布较为复杂，其值沿裂缝尖端到裂缝开口方向迅速减小。随着列车运行速度的增加，轨枕裂缝内动水压力增大。裂缝几何形态是影响轨枕裂缝内动水压力的重要因素，在高速列车荷载与水的耦合作用下，随着裂缝长度的增加、开口量的减小，裂缝内动水压力显著增大。

(2)无砟轨道轨枕周边裂缝为张开型与剪切型同时存在的复合型裂缝，且裂缝主要以剪切型破坏为主，裂缝的等效应力强度因子随列车运行速度增加、裂缝开口量减小而增大，裂缝尖端的等效应力强度因子与裂缝长度呈正相关关系。

(3) 双块式无砟轨道枕边裂缝的疲劳寿命主要受裂缝初始长度控制，裂缝初始长度增加，裂缝疲劳寿命减小，当裂缝的失稳长度与初始长度之差小于0.05 m时，应当及时对轨枕周边裂缝进行修补。此外，列车运行速度是枕边裂缝疲劳寿命的关键影响因素，速度350 km/h列车动荷载对应裂缝扩展速率大约是速度250 km/h列车动荷载对应裂缝扩展速率的1.5～2倍，列车运行速度的提升显著增大了枕边裂缝的扩展速率。