高速铁路桥上无缝道岔结构力学状态预测方法

马卓然，高 亮

(北京交通大学 土木建筑工程学院， 北京 100044)

高速铁路桥上无缝道岔轨道系统集合了无缝线路、无缝道岔、无砟轨道和大跨桥梁等技术难点，是高速铁路最为敏感典型的区域[1]。由于其结构间相互作用复杂，受力变形发展规律较难把握，无法利用传统理论分析手段准确判断和预知轨道力学状态[2]。而在长期服役过程中，轨道系统直接暴露在外部环境中，会受到温度循环、列车荷载等复杂外部因素影响，引起结构力学状态异常，进而影响系统的运营安全[3]。因此，有必要建立数据驱动的结构力学状态预测方法，提早掌握结构的力学行为，辅助评估轨道系统的健康状况。

目前，在轨道状态预测方法方面，大多研究主要通过建立不同的轨道不平顺预测模型，预测轨道几何劣化，评估轨道几何质量。较流行的预测方法包括ARIMA模型[4-5]、灰色模型[6-7]、贝叶斯网络[8]、人工神经网络[9-10]以及多种方法结合的组合模型[11-12]。上述方法重点关注轨道几何状态，并未涉及结构的力学本质。由于几何不平顺数据与反映力学状态的受力变形数据在特征上差异较大，故既有不平顺预测方法较难实现结构力学状态的准确预测。此外，也有极少数研究采用线性回归、神经网络等方法对轨道结构的力学状态进行预测[13]，但研究仍处于起步阶段，预测精度和稳定性均有待提高。

本文依托京沪高速铁路桥上42号道岔监测工点，基于监测数据的基本特征，以气温序列为输入，以反映结构健康状态的钢轨温度、钢轨纵向应力和尖轨伸缩位移为目标，构建遗传算法优化的Elman神经网络预测模型(GA-Elman)。通过对比不同气温输入形式和不同模型构架的预测性能，验证方法的优越性。

1 监测数据特征

本文监测数据源于京沪高速铁路天津南站42号大号码道岔监测工点。该工点的具体测点布置如图1所示，“数字”+“号”为传感器编号。工点共计38个测点，包括气温、轨温、钢轨纵向应力、尖轨伸缩位移等指标。其中，尖轨伸缩位移采用视频图像监测(0.5 h/次)，其余指标采用光纤光栅传感器(15 min/次)。通过前期研究[14]发现，不同状态指标的时程变化规律类似，且与温度存在不同程度的相关性。在各项指标中，钢轨温度的变化会直接影响轨道结构的受力变形，钢轨纵向应力异常可能导致胀轨跑道甚至断轨，尖轨伸缩位移过大会导致道岔卡阻。可见，这三项指标均与结构状态密切相关，通过预测其发展变化可间接掌握结构的健康状况，因此，本文以这三者为例进行预测。

图2为不同监测指标的时程变化。不同状态监测指标在时程上与气温跟随性良好，变化周期一致，为1 d，但不完全同步，与文献[15]的观点一致，这主要是由于轨道系统光照不均匀，空间传热存在滞后效应所致。为进一步分析各指标与气温的相关程度和主要相关频率，对各指标与气温进行相干分析。图3为钢轨纵向应力4号与气温的相干分析结果。从图3可以看出，应力4号与气温在0.98×10-5～1.74×10-5/s的范围内相关程度较大，而在其他频段相关程度较小。当频率为1.30×10-5/s，即周期约为1 d时，相干系数达到最大值0.78，这与时域分析结果一致。

图2 监测指标的时程变化曲线

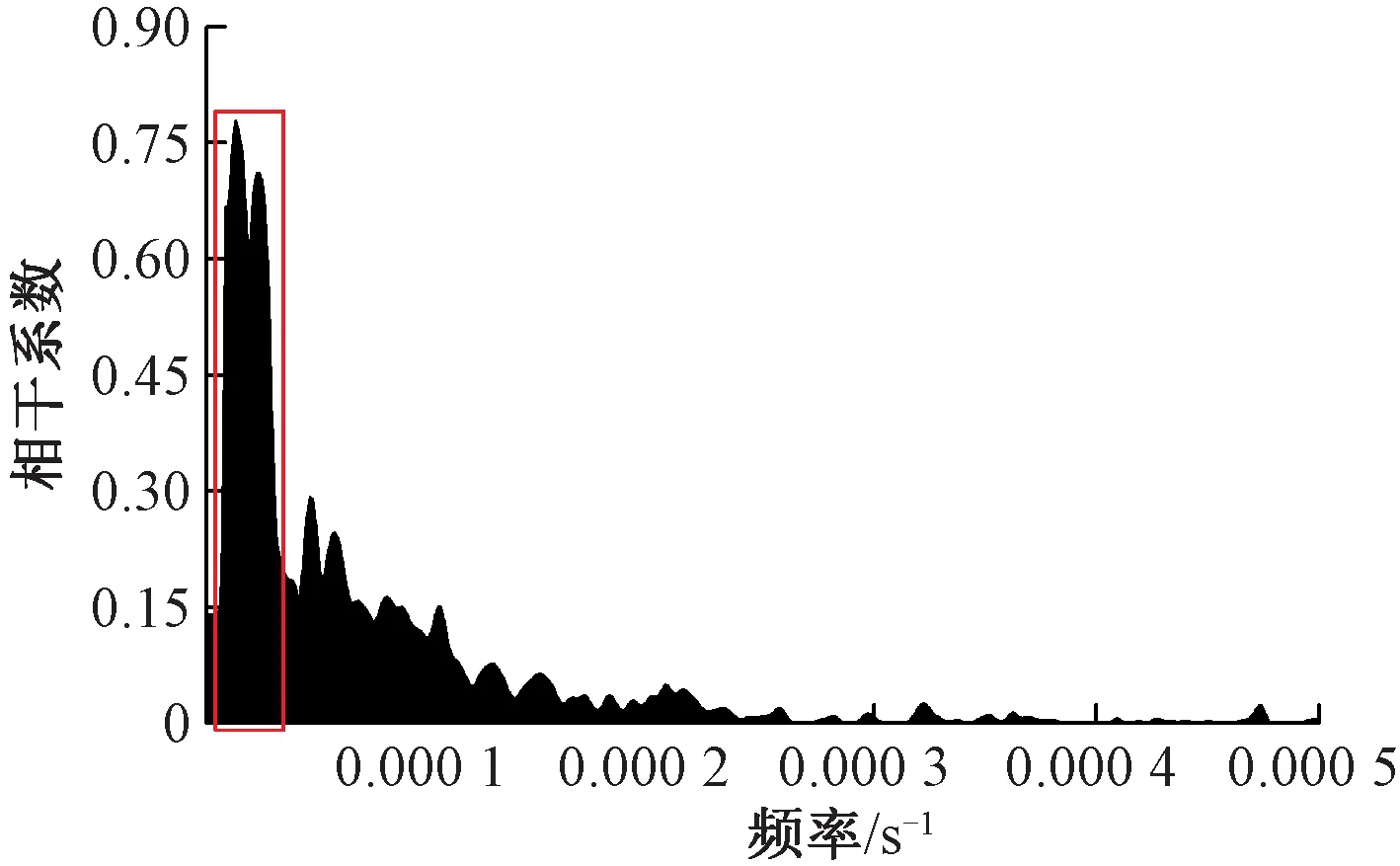
图3 钢轨纵向应力4号与气温的相关程度

2 预测框架

2.1 原始气温序列化

由于各指标与气温的时频关联性较强，且在实际中气温可通过气象预报直接获得，故采用气温作为预测模型的输入。轨道结构状态不仅与当前的温度荷载有关，温度力无法及时放散而在结构内部的累积也会对结构的受力变形发展造成影响[14-15]，因此考虑以气温时间序列的形式输入预测模型。为确定输入的气温数据点数，建立多元线性回归模型分析考虑不同气温范围对力学状态指标拟合程度的影响，即

yt=α0+α1Tt-n+1+α2Tt-n+2+ …+αnTt

(1)

式中：yt为t时刻的指标监测值；n为考虑的气温数据点个数；Tt为t时刻的气温值；α0,α1, …,αn为待定系数。

如图4所示,随着输入气温数据点数的增加，气温对力学状态指标的拟合程度先逐渐提高，后趋于稳定，最终可达0.845 6～0.968 4。这表明，相比以单点气温为输入，以一定范围的气温序列输入模型，能够更好地模拟各状态指标的发展变化。

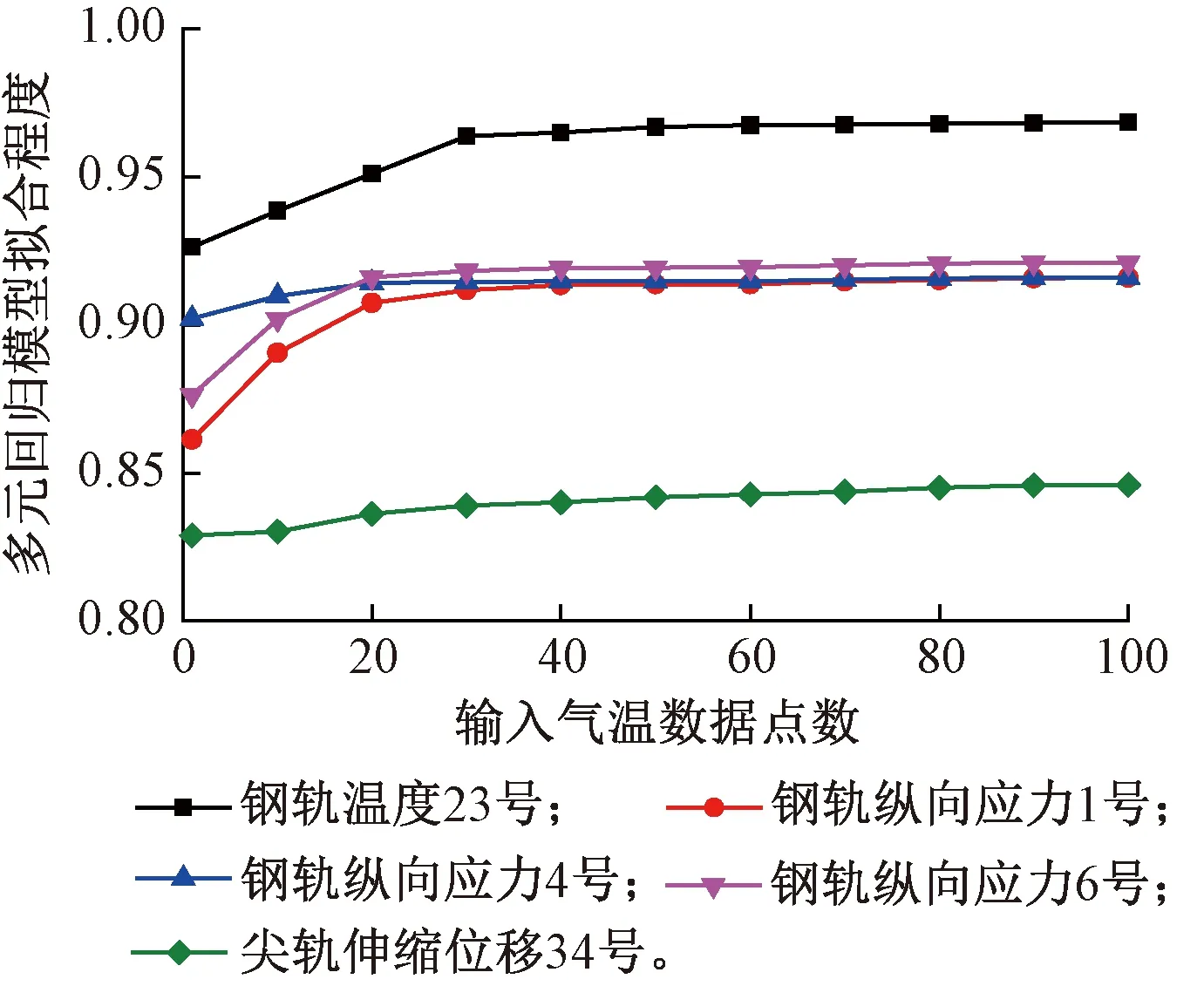
图4 输入气温范围对状态指标拟合程度的影响

因此，在预测前，对原始气温进行序列化预处理，即

(2)

式中：[·]为处理前后的输入气温数据集；p为各指标所对应的最优气温时间序列长度。结合计算效率和拟合精度，综合考虑各指标的不同测点，确定预测轨温、钢轨纵向应力和尖轨伸缩位移所输入的气温数据点数分别为60、40和90。

2.2 Elman神经网络

Elman神经网络是一种具有内部时延反馈功能的循环神经网络[16]，其网络的结构如图5所示，包括输入层、隐藏层、承接层和输出层四个层次。其中，承接层可用于存储隐含层上一时刻的输出值，从而形成一种短期记忆。Elman神经网络可将隐含层的输出通过承接层的延迟和存储与隐含层的输入自链接，从而能够学习序列数据的时序特征[17]，因此十分适用于本文所研究的时间序列预测问题。

图5 Elman神经网络拓扑结构

网络的计算过程可以表示为

xc(t)=x(t-1)

(3)

x(t)=f(w1(u(t-1)+w2xc(t)))

(4)

y(t)=g(w3x(t))

(5)

式中：u(t-1)为网络的输入值；x(t)为隐含层的输出值；xc(t)为承接层的输出值；y(t)为网络的输出值；w1、w2和w3分别为输入层对隐藏层、承接层对隐含层和隐含层对输出层的权重；f(·)和g(·)分别为隐含层和输出层的激励函数。

本文以误差平方和为损失函数，当训练达到最大训练次数或满足精度10-5时则结束训练。为提升模型的预测性能，通过反复试算法对隐含层节点数进行寻优，如图6所示。基于均方误差最小准则，确定轨温、钢轨纵向应力和尖轨伸缩位移的隐含层节点数量分别为10、5和2。此外，将隐含层和输出层的激励函数分别设为tansig和purelin，训练函数设为trainlm，学习率设为0.001。

图6 隐含层节点数量对模型性能的影响

2.3 遗传算法

遗传算法(GA)是模拟生物进化和自然遗传机制的全局优化算法[18]。它将“适者生存”的规则应用于编码组[17]，通过逐代的选择、交叉和突变获得最优个体。主要训练过程如下。

(1)个体初始化：本文采用实数编码来初始化个体，并将种群规模设为10。

(2)适应度值F计算：适应度值越小的个体越优，本文采用的适应度函数为

(6)

式中：Yi为实际值；yi为预测值；n为样本点总数。

(3)选择：以一定的概率从上一代中选择个体到新的一代。本文采用轮盘赌的方法进行选择。

(4)交叉：随机交换两个个体的一个或多个位置上的信息以产生新的个体。本文采用单点交叉法，交叉概率设为0.4。

(5)突变：通过改变个体某些位置的信息以产生更好的个体。本文突变概率设为0.05。

(6)终止：当迭代次数达到最大值50，或(Fmax-Fmin)/Fmin小于0.05时，计算终止。

2.4 预测步骤

基于上述方法，可构建遗传算法优化的Elman神经网络预测框架(GA-Elman)。通过气温序列化处理，利用最优气温序列对轨道结构的力学状态指标进行预测，如图7所示。其中，遗传算法用于神经网络结构参数的全局寻优，从而避免Elman神经网络陷入局部最小，提高网络收敛速度；Elman神经网络用于结构状态的预测。

图7 预测框架

主要预测步骤如下：

Step1根据预测目标，确定神经网络的拓扑结构，从而计算获得遗传算法需优化的个体长度。

Step2采用实数编码方式对种群个体初始化。

Step3将原始气温数据进行预处理，生成温度时间序列，输入所建模型。

Step4通过遗传算法选择、交叉、变异、适应度值计算对个体进行逐代优化，获取最优个体。

Step5将最优个体赋予神经网络初始参数，并反复训练，使模型预测性能达到最佳，测试即可获得预测结果。

3 预测结果

以监测工点2017年8月至2018年7月各测点的监测数据作为数据集，进行轨道结构力学状态预测。其中，前95%的数据用于训练，后5%的数据用于测试。从不同气温输入形式和不同预测框架两个方面，对所提出模型的预测性能进行验证。

3.1 不同气温输入形式的预测性能对比

为对比气温输入形式不同对预测精度的影响，分别以单点气温和气温时间序列为输入，利用GA-Elman模型进行预测，部分测点的预测结果如图8所示。

图8 不同指标的预测结果

从图8可以看出，所建预测模型对于各项监测指标均具有良好的预测性能，预测结果的整体变化规律与实际监测值均保持一致。与基于单点气温的预测结果相比，采用气温序列进行预测，预测值与实测值吻合度更高，并且能够更好地模拟峰值的变化，峰值处的预测偏差相对较小。由此说明以气温序列为输入的预测性能更优。

3.2 不同模型的预测性能对比

为验证所建模型的优越性，将其从预测精度和预测可靠性两个方面与多元线性回归和基础Elman神经网络进行对比。各模型均以气温序列为输入，选择平均绝对误差MAE、均方根误差RMSE和误差标准偏差S作为评价依据。MAE和RMSE直接反映预测误差大小，即预测精度；S反映误差的离散程度，间接表征了预测结果的可靠性。考虑预测目标有多个测点，取各测点评价指标的均值作为最终结果，各指标的具体计算方法为

(7)

(8)

(9)

式中：m为各目标不同测点结果取平均值；N为目标的测点数量；n为测试样本点数；Oij、Pij和eij分别为预测目标第i个测点第j个样本点的监测值、预测值和预测误差。

各预测模型的误差评价指标如表1所示，对比可发现，GA-Elman混合模型的预测性能最佳，Elman神经网络次之，多元线性回归最差。这说明：一方面，通过遗传算法优化能够使网络预测精度更高；另一方面，仅通过线性拟合较难实现对轨道结构状态的准确预测。考虑预测目标量值的差异，为便于对比，表2对GA-Elman模型相较于其他模型的优越程度(即评价指标降幅)进行了量化，计算式为

表1 不同模型的预测误差对比

表2 GA-Elman模型相较其他模型的误差降幅

R1/2=(E1-E2)/E1×100%

(10)

式中：R1/2为方法2相对于方法1的指标降幅；E1和E2分别为方法1和方法2的评价指标值。

从表2中可发现，相较其他模型，GA-Elman模型的预测精度和预测结果的可靠性均明显提高。预测精度方面，相比于多元线性回归，GA-Elman的MAEm平均下降39.48%，RMSEm下降29.10%；相比于Elman神经网络，MAEm平均下降16.17%，RMSEm平均下降8.52%。预测可靠性方面，各目标的Sm相比于多元线性回归和Elman神经网络分别平均下降10.92%和6.84%。

此外，为对比GA-Elman模型和Elman的计算结果稳定性，以RMSE为依据，分别利用两个模型对各指标进行10次训练并预测，结果如图9所示。

图9 GA-Elman模型和Elman神经网络的预测稳定性对比

从图9可以看出，采用Elman神经网络对同一测点进行多次测试，RMSE的波动剧烈且数值偏大，而GA-Elman的RMSE无明显波动且均处于较低水平。这表明利用遗传算法对网络优化能有效提高模型的稳定性。

综合上述分析，认为采用GA-Elman混合模型的预测精度最高，预测结果最为可靠稳定，能够较好地应用于轨道结构力学状态的预测预警。由于数据特征的相似性，所提出预测方法主要适用于轨道结构状态数据预测。在实际应用中，通过训练调整网络模型参数，即可应用于各种轨道系统和各项状态指标的预测中，可操作性较强，计算效率较高。

4 结论

本文基于监测数据的分析，构建了遗传算法优化的Elman神经网络时间序列预测模型，以序列化后的气温为输入，对钢轨温度、钢轨纵向应力和尖轨伸缩位移三项反映结构状态的监测指标进行预测，主要结论如下：

(1)基于监测数据的时频分析，以气温最优序列为模型输入，相较于单点气温输入形式，以温度序列为输入的形式能够使模型的预测精度得到较大的提高。

(2)利用遗传算法对神经网络优化，能够使网络参数取值更为合理，从而明显改善模型的预测精度以及预测结果的可靠性。

(3)GA-Elman预测模型相较多元线性回归和基本Elman神经网络，MAEm分别下降39.48%和16.17%，RMSEm分别下降29.10%和8.52%，Sm分别下降10.92%和6.84%，说明其预测结果最为准确可靠。

综上，GA-Elman模型预测性能最佳，可作为桥上无缝道岔轨道系统结构力学状态预测的有效方法，能够准确感知轨道结构的力学性能发展变化，为实现轨道系统结构隐患的预测预警提供支持。