沙粒内禀尺度对道床宏细观力学特性影响研究

肖 宏，张智海，王宏阁，崔旭浩

(1.北京交通大学 土木建筑工程学院， 北京 100044；2.北京交通大学 轨道工程北京市重点实验室， 北京 100044)

我国西北地区荒漠化严重，铁路道床积沙现象普遍。散体道床在列车荷载作用下，沙粒会不断侵入道床填充道砟空隙，改变原有的道床颗粒组分及级配。随着道床中沙粒含量的增加，轨道结构易出现拱道、道床板结、钢轨低接头、三角坑等工务病害。这不仅使轨道几何形位难以保持，还会加大线路养护维修工作量[1-2]。此外，细沙的灌入轻则降低道床服役性能，重则导致扣件锈蚀断裂及钢轨永久变形，直接影响行车安全[3]。因此，开展风沙区铁路道床宏细观力学特性研究非常必要。

沙粒侵入引发一系列线路服役状态问题，受到诸多铁道工程研究者的关注。由于物理试验成本较高且试验结果离散性大、影响因素难以控制[4]，有学者采用离散单元法(DEM)来研究沙粒与道砟之间的宏细观力学特性。严颖等[5]建立了桶状离散元试样，对道砟和细沙颗粒进行了数值模拟，分析了不同含沙率下有效变形模量差异性，但在研究过程中将沙粒粒径放大了20倍。高亮等[6]建立了三维道砟箱剪切模型，研究了黄沙对道床剪切性能的影响，将黄沙粒径直接视为4～9.5 mm进行模拟，并未深究沙粒合理模拟尺度的选择问题。以上研究表明，针对沙粒灌入，对道砟材料力学特性影响的数值试验研究忽略了沙粒粒径尺度效应的影响，未能准确模拟沙粒与道砟相互作用关系及颗粒之间接触力传递规律，因而不能从本质上揭示道床内部多元混合颗粒之间的相互作用原理。可见，要探明含沙道床力学特性，首先要解决数值模拟中沙粒粒径的合理选择问题。

对于颗粒材料的尺度研究，目前主要关注宏观、细观、微观3个层次[7]。不同粒径尺度是相对的，不是固定不变的，应视研究问题而定。在细、微观层次，颗粒材料可以被量化为不同粒径的细小颗粒集合体，其力学性质随颗粒粒径量变逐渐引发颗粒集合体特性的质变。在研究沙粒与道砟之间的相互作用关系时，由于沙粒粒径较小，全尺度道床模型中沙粒数量可能达到数千万甚至上亿，现有的计算条件根本无法精确模拟。为模拟细小颗粒的力学特性，许多学者利用颗粒缩放法来处理细小颗粒尺寸效应问题，并将其广泛应用于工程研究中。任建莉等[8]利用相似理论和量纲分析法，对铸铁煤粉的放大颗粒进行了微观参数标定，验证了颗粒缩放理论的正确性。李永祥等[9]利用颗粒缩放原理，将小麦粉粒径放大了6倍，进行了“Hertz-Mindlin with JKR”接触模型参数标定。Sakai等[10]在流化床数值试验中，将细颗粒体用粗颗粒进行替换，结果表明，粗颗粒模型可以较为准确的模拟原始颗粒材料的力学特性。Weinhart等[11]建立了粗颗粒筒仓离散元仿真模型，提出了在高度局部化系统中空间粗颗粒宽度选择的重要性。但以上研究都是利用颗粒缩放法来表征单一颗粒力学特性，而风沙道床属于多元混合颗粒体系，内部颗粒之间传力方式复杂多样，其粒径缩放原理是否仍然适用还需进一步验证。尤其在沙粒粒径缩放对道床力学特性的影响研究方面，目前少有涉及。

为描述风沙道床数值模拟过程中不同沙粒尺寸与道砟粒径的关系，将数值模型中沙粒最小颗粒粒径与道砟最大颗粒粒径的比值，定义为内禀尺度。该指标重在反映可变沙粒粒径与不变道砟颗粒粒径的关系，是风沙道床数值模型内部颗粒跨尺度作用的一种体现。

基于上述分析，本文将从不同沙粒粒径的填充方法入手，基于颗粒缩放原理提出一种新的研究多元混合颗粒粒径尺度效应的方法——“胞分法”。该方法是基于细胞分裂分化的思想，通过阈值人为控制胞体的分裂分化数量与次数，严格保证局部区域内新产生的胞体与原胞体所占空间大小相同。本文借助胞分原理来保证了不同沙粒尺寸下道砟空隙中沙粒质量守恒，进而研究沙粒粒径尺寸对道床宏细观力学特性的影响，揭示多元混合颗粒之间力链传递及演变规律，给出数值试验沙粒的合理尺寸，以期为风沙区铁路道床力学特性研究提供先决条件。

1 胞分法分析模型

1.1 胞分法理论模型

风沙道床是多元混合材料相互作用构成的复杂颗粒体系，其力学特性取决于颗粒体系的细、微观作用力。不同沙粒尺寸对道床结构产生不同的力学效应，而沙粒比表面积和质量随粒径的改变而逐渐变化，会影响道砟与沙粒之间接触的产生[12]。颗粒缩放法[8-10]虽能模拟细小颗粒，但仅用于单一颗粒力学特性的研究，而针对多元混合颗粒研究未必适用，且风沙道床颗粒体系复杂多变，需保证道砟空隙含沙量不变，减少计算误差，确保计算结果真实可靠。

风沙道床颗粒数量较多，利用PFC3D模拟，存在小颗粒悬浮、模型平衡困难、计算效率低等问题，且在分析多根轨枕长度的线路时，存在局限性。已有文献[13-15]表明，二维模型可以反映道砟颗粒之间的接触特性，因此本文拟采用PFC2D模型进行分析。

为考虑沙粒粒径对道床受力状态的影响，保证道砟空隙含沙量不变，道床体系沙粒质量守恒，本文将单个沙粒看成一个胞体，新产生的沙粒视为胞元，引入阈值含沙量γ来建立原胞体与新胞元之间的联系，即

(1)

(2)

(3)

(4)

(5)

式中：ms为道床中沙粒总质量；mb为道砟颗粒总质量；Ns为沙粒数量；Nb为道砟颗粒数量；ρs为沙粒密度；Vis为第i个沙粒的体积；ρb为道砟密度；Vjb为第j个道砟的体积；Sis为第i个沙粒的面积；Sjb为第j个道砟的面积；Ts为沙粒模拟单元的厚度；Tb为道砟模拟单元的厚度。

若沙粒采用单位圆盘模拟，垂直于平面方向道砟颗粒厚度Tb与沙粒厚度Ts均为单位厚度。由式(4)和式(5)可得，单个颗粒体积与圆盘面积数值相等，含沙量γ与沙粒数量、颗粒所占面积正相关，且第i个沙粒面积Sis与沙粒粒径d2成正比。因此要保证道砟空隙中含沙量不变，需确定沙粒数量与沙粒粒径之间的关系。

本文拟通过控制分裂次数与新生胞元的半径来逐渐逼近沙粒的真实细、微观作用效果。在模拟时，首先采用先张后缩法将沙粒粒径放大10倍并视为原胞体，也可称为一分胞体，然后利用fish语言来保证每次分裂产生的新胞元粒径相同，且胞元之间为最密排列方式，减小由于颗粒错动、重新排列造成的计算误差，缩减离散元模型的平衡时间。

在利用胞分法建立不同沙粒粒径离散元模型时，将沙粒粒径缩放区间离散化，文献[5]拟定了沙粒粒径缩放上限值为10。考虑计算效率和模拟精度等问题，将分裂次数n的上限值取为8，使第8次分裂后的沙粒粒径处于实际粗沙粒径1 mm附近。分裂次数和沙粒胞元半径的关系为

(6)

式中：R1为一分胞体的沙粒半径；Rn为第n次分裂后沙粒半径。

沙粒胞体分裂过程见图1，图1中黑色虚线表示原胞体轮廓，绿色虚线是各个胞元质心的连线。通过局部坐标反演的方法，利用质心线构成正三角形、正方形等几何体，推算出以原胞体质心为中心的周围各个胞元质心的位置坐标。借助fish语言将每次分裂的沙粒质心坐标导入PFC中进行颗粒质心更新计算，实现沙粒的分裂分化过程，使沙粒粒径逐渐减小，向真实沙粒粒径逐渐逼近，表1是道床内部沙粒粒径与分裂次数的对应关系，其中，d为中细沙粒的真实颗粒粒径，一般在0.25～0.5 mm之间取值。

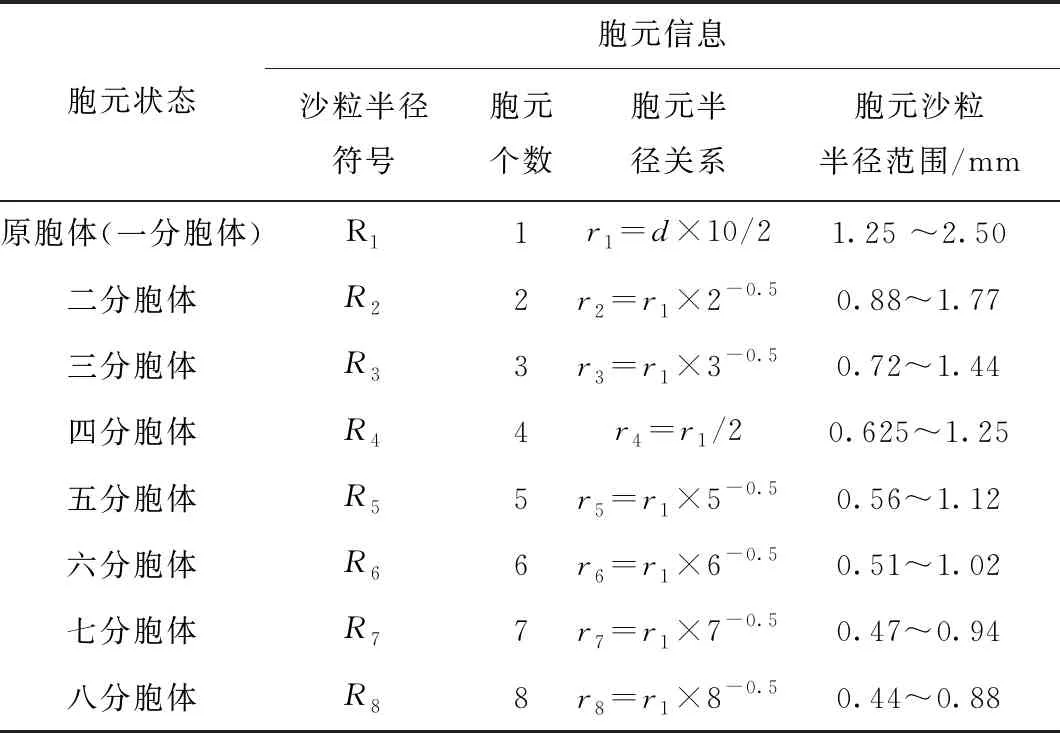
表1 沙粒胞元颗粒信息统计

图1 沙粒胞体分裂过程

1.2 颗粒流模型的构建

1.2.1 轨道结构离散元模型

在建立风沙区轨道结构离散元模型之前，需建立精细化的道砟颗粒模型。已有研究表明[16]，道砟颗粒外形、级配、棱角的各向异性等是影响道砟精确模拟的关键。为考虑道砟颗粒棱角及外在形态特征[17-18]，本文利用三维逆向工程软件提取了道砟三维廓形[19]，沿着最长轴线进行投影得到道砟颗粒二维廓形文件，通过自编fish语言导入PFC中生成不规则道砟颗粒，并按照既有线一级碎石道砟颗粒级配生成道砟颗粒，粒径范围为25～63 mm。

图2 风沙区轨道结构离散元模型

结合现场实际轨道铺设情况，道床厚度取0.35 m，道砟用clump单元模拟，沙粒采用ball单元模拟。一般而言，车轮荷载影响区域范围[20]为5根轨枕，为消除边界效应的影响，特利用块体叠加拼装法生成7根轨枕长度的风沙道床仿真模型。轨枕采用ⅩⅡ型混凝土枕，以颗粒簇块体方式导入道床模型中；扣件采用两个半径为35 mm的ball单元模拟；综合考虑60 kg/m钢轨的实际界面尺寸，离散元模型中采用直径为0.15 m的28个小球规则排列黏结而成，利用等质量法[13]计算单个颗粒密度约为510 kg/m3。考虑钢轨与列车之间的相互作用，根据一个转向架的距离来设置两个加载颗粒的间距，利用fish语言将荷载时程曲线分别施加在3号和4号轨枕中间及7号轨枕左侧的加载颗粒上，来模拟车轮与钢轨之间的荷载传递。采用“胞分法”建立不同沙粒粒径的多尺度轨道结构离散仿真模型。

1.2.2 本构模型

表2 离散元模型细观参数

2 现场试验及模型验证

2.1 现场试验

为研究沙粒作用对道床力学特性的影响，在风沙严重的甘万铁路昌吉高勒站和巴音杭盖站区段开展了现场轮轨力与道床加速度动测试验，分别布置钢轨垂向力测点和道床加速度测点。测得钢轨垂向力最大为117.69 kN，道床最大加速度为1.41g。

2.2 列车荷载施加

为研究实际列车荷载作用下风沙道床沙粒多尺度效应，以现场速度58 km/h试验列车C70E的实测轮轨垂向力为依据，利用程序语言对实测曲线相邻数据点进行了加密处理，生成了荷载数据文件，采用table命令将荷载数据文件导入到PFC中，并将其施加到图2(b)中的车轮上。现场实测轮轨垂向力时程曲线见图3。为准确捕捉图3中的荷载曲线峰值数据，在数值加载过程中将计算时步调至10-7～10-8之间。考虑列车循环荷载特性及离散元模型的计算效率问题，本文选取了两节车厢8轴荷载模式的时程曲线来模拟实际列车荷载，见图4。

图3 现场实测轮轨垂向力时程曲线

图4 试验现场C70E敞车示意(单位：mm)

2.3 模型可靠性验证

为验证模型的正确性，将图4中现场实测的轮轨垂向力荷载谱施加到本文所建的离散元模型中，计算得到风沙区道床振动加速度最大峰值为1.44g，现场实测道床振动加速度最大峰值为1.41g，试验值与离散元模拟值仅相差2.13%，数值吻合度高。现场实测道床加速度时程曲线见图5，离散元仿真道床加速度时程曲线见图6。对比图5和图6可知，在列车荷载作用下二者的曲线走势及增长幅值变化规律几乎相同，实测加速度值因受现场环境、轮轨噪声信号、测试信号线固定不到位、线路不平顺等因素的干扰，基线较粗，与数值分析结果细部形态略有差异，但不影响道床加速度幅值随时间的变化趋势。综上所述，本文从数值大小和图形规律都验证了模型的可靠性，也说明了离散元模型中微观接触参数可以用于沙粒尺寸的研究。

图5 现场实测道床加速度时程曲线

图6 离散元仿真道床加速度时程曲线

3 道床受力特性分析

为揭示细沙颗粒大小对道床力学行为的影响，以及纯粹的颗粒粒径尺度缩放是否会引起道床受力体系的改变，论文利用胞分法建立了8种不同沙粒粒径的离散元仿真模型，从宏细观角度分析了不同沙粒粒径作用下道床的力学特性，数值试验方案见表3。

表3 不同沙粒粒径计算方案

3.1 道床细观接触力演变规律分析

3.1.1 平均接触力分析

道砟颗粒平均接触力是衡量道砟接触状态的重要指标，可以反映道床内部道砟颗粒的平均受力情况。为研究分析方便，将8轴荷载的各轴按照从左到右依次编号，列车轴次与道砟平均接触力的关系曲线见图7。

图7 道砟平均接触力变化

由图7可知，当沙粒处于一分胞体状态时，道砟平均接触力最大为139.557 N；当沙粒处于八分胞体状态时，道砟平均接触力最大为83.306 N，相对减小了40.31%。随着沙粒分裂次数的增加，沙粒内禀尺度逐渐减小，平均接触力相对减小百分比逐渐趋于0，道砟平均接触力逐渐收敛趋于定值。六分胞体时，道砟平均接触力变化幅度较小，因而可以反映实际沙粒的作用效果。这是由于在含沙量不变的情况下，随着沙粒粒径的减少，道床中沙粒数量成倍增加，使道床内部颗粒接触增多，力链的传递和延伸方向逐渐增多，道砟颗粒之间的接触力逐渐减小，平均接触力也逐渐减小。

3.1.2 接触力概率密度分析

为从细观角度揭示不同沙粒粒径作用下道床内部颗粒接触力分布规律，采用张科芬等[4]、Liu等[27]提出的度量颗粒间力大小的概率密度曲线，衡量在一定范围内颗粒接触力出现的概率，借此直接观察颗粒体系中强接触力与弱接触力分布规律。对于风沙道床散粒体系，内部颗粒接触力大小是离散且有限的，因此可利用fish语言遍历颗粒之间的接触力，接触力的概率密度为

(7)

式中：x为接触力的离散值，介于[0，b]之间，b值取决于接触力区间上限值；v(x)为颗粒体系接触力小于x的个数；N为颗粒体系总的接触对；F(x)为接触力分布函数；p(x)为接触力概率密度函数。接触力概率密度统计结果见图8。

由图8可知，随着颗粒间接触力的逐渐增大，接触法向力与接触切向力概率密度逐渐减小，且小的接触力占比更高。道床结构不受外力时，随沙粒胞分次数的增加，沙粒粒径逐渐减小，无论是法向接触力还是切向接触力，概率密度分布曲线都越来越陡，最大接触力b值越来越小，可以明显看出三分胞体后，接触力概率密度曲线变化趋势逐渐趋于稳定，出现大接触力概率愈小，小接触力概率愈大；峰值荷载作用下最大接触力概率密度随沙粒粒径减小而逐渐减小，道床接触法向力与切向力大小趋于均匀化。对比可知，法向接触力在第五次分裂后概率密度曲线趋于稳定，而切向接触力在第六次分裂后概率密度才趋于稳定，说明沙粒粒径对切向接触力分布影响更大。峰值荷载作用下道床内部法向和切向接触力离散值是自重作用下的5倍，表明列车荷载作用是道床内部产生强接触力的主要原因，弱接触力是道床颗粒体系接触力的主要表现形式。

综上可知，沙粒内禀尺度会影响道床颗粒间的接触力分布规律，且对峰值荷载作用下接触力分布影响更为显著。为减小沙粒粒径对数值试验的影响，可选择六分胞体沙粒粒径进行模拟计算，以保证计算结果的可靠性，揭示沙粒对道床受力影响的内在机理。

3.1.3 接触力方向演变规律分析

为更加直观地分析沙粒内禀尺度对道床内部颗粒体系接触力各向异性演变规律的影响，分组统计了峰值荷载作用下各方向接触力的数目及各接触力绝对值累计值(接触力合力)，利用自编CAD小程序绘制了道砟颗粒法向接触合力和切向接触合力各向异性玫瑰图，见图9和图10。图9和10中同心圆半径大小代表不同等级接触合力量值，圆盘外围角度表示各组接触合力方向。由于绘图前，设置了绘图基准力，图9和10中所显示的是各组接触合力量值，该量值是各组接触力绝对值累计值除以基准力得到，因此无量纲。图9的绘图基准力为100 kN，图10的绘图基准力为50 kN。

各组法向接触合力分布；平均法向接触合力。

各组切向接触合力分布；平均切向接触合力。

3.2 道床应力场细观分析

为了量化不同沙粒粒径作用下，道床应力场的变化规律，选取了列车荷载作用影响最大区间，通过自编fish语言提取单个颗粒的平均接触应力，按照一定比例绘制了峰值荷载作用下不同沙粒粒径的道床应力场分布云图，见图11。

图11 不同沙粒尺寸下道床应力场分布

由图11可知，列车荷载作用下风沙道床内部应力分布较为均匀，低应力(绿色区域)分布面积较大，高应力(红色区域)仅分布在道床局部区域，且轨枕底部应力较大，而枕侧区域平均应力较小，这与轨枕传力方式、枕底颗粒接触数目密切相关。通过观察发现，随着沙粒内禀尺度的逐渐减小，沙粒数量倍增，道床中高应力区域逐渐减小，低应力区域占比越来越高，道床应力均匀化程度显著增强。一分胞体道床内部高应力区域占比较高，但随着沙粒的分裂次数的增加，高应力区域明显减少，直到六分胞体时，颗粒之间的强接触力减少，道床应力衰减幅度明显降低，道床内部高应力区域占比趋于稳定，处于低应力状态。这是由于列车荷载与颗粒接触数目是影响道床细观应力状态的主要因素，在特定的列车荷载作用下，颗粒接触数目受颗粒数量的影响较大。一般而言，颗粒数目越多，细观接触面越大，颗粒之间接触配对相对容易，颗粒之间的接触对愈多，作用力相对分散，强接触力不易产生，道床内部趋于低应力状态。

为进一步探究沙粒内禀尺度与道床内部应力的作用关系，统计了峰值荷载作用下，不同沙粒粒径的道床最大应力和平均应力，见图12。由图12可知，不同沙粒粒径的道床内部应力差异性较大，且随着沙粒粒径的减小，即沙粒胞元个数的增加，道床最大应力和平均应力也逐渐减小；自五分胞体后，道床最大应力在375.124～380.225 kPa之间，平均应力在32.206～32.501 kPa之间，应力幅值变化不大，沙粒粒径对道床应力的作用效果减弱，这与图11道床应力分布云图得出的结论一致。

图12 不同沙粒粒径作用下道床应力值

道砟颗粒之间的接触力大小和接触数目是影响道床内部平均应力的关键，而沙粒的侵入改变了原有道床的受力体系，颗粒之间的无规则排列，导致接触力分布方向的各向异性，且随着沙粒粒径的减小，沙粒数量愈多，道床内部接触数目愈多，作用力的传递及力链延伸方向多样，道床内部的强接触力愈少，颗粒之间的最大接触力也逐渐变小。因此，道床的最大应力和平均应力随沙粒粒径的减小而逐渐减小，但当沙粒粒径减小到一定程度时，沙粒内禀尺度对道床作用减弱，出现了道床应力变化稳定点，这为沙粒侵入道床数值试验最小颗粒尺度的选择，提供了理论依据。

4 结论

为研究沙粒内禀尺度对道床宏细观力学特性的影响，确定风沙区道床数值试验沙粒粒径的合理尺度，考虑道砟空隙中沙粒质量守恒和无相互重叠原则，首次采用“胞分法”建立了不同沙粒粒径尺度的精细化轨道结构离散元模型，分析发现沙粒粒径对道床宏细观力学特性有明确影响。

(1)沙粒粒径会影响道砟的平均接触力大小。沙粒处于一分胞体状态时，道砟颗粒最大平均接触力为139.557 N；沙粒处于八分胞体时，道砟最大平均接触力为83.306 N，相对减小了40.31%；随着沙粒胞分次数的增加，沙粒粒径逐渐减小，道砟平均接触力也逐渐减小。

(2)沙粒内禀尺度会影响道床颗粒间的接触力分布规律，对峰值荷载作用下接触力分布影响更为显著。随着颗粒间接触力的逐渐增大，接触法向力与接触切向力概率密度逐渐减小，小接触力占比更高。为减小沙粒粒径对数值试验的影响，建议选择六分胞体沙粒粒径进行道床受力分析，以保证研究结果的可靠性。

(3)沙粒内禀尺度主要影响切向接触合力量值分布方向各向异性，而对呈“蝴蝶状”分布的法向接触合力量值分布方向影响较小。随着沙粒内禀尺度愈减，即逐渐逼近真实沙粒粒径时，法向接触合力量值各向异性增强，而切向接触合力量值在不同沙粒粒径作用下接触方向分布形态各异，接触力量值主分布方向不断变化，各向异性更为显著。另外，接触合力方向玫瑰图也再现了随着沙粒粒径增大，道砟颗粒接触力由弱到强的演变过程。

(4)沙粒粒径与道床内部应力分布存在关联。随着沙粒粒径的减小，道床最大应力和平均应力都逐渐减小。当沙粒粒径减小到一定程度时，沙粒内禀尺度对道床作用减弱，出现了道床应力变化稳定变化点。

(5)通过对不同沙粒尺寸下道床的宏细观力学特性进行分析，采用球形颗粒模拟沙粒时，沙粒半径建议取为0.51～1.02 mm，即沙粒内禀尺度比为0.016 2，可以较为真实的模拟沙粒与道砟的实际作用效果。