考虑旅客换乘的高速铁路列车运行调整研究

张 璞，赵 鹏,2，乔 珂，温鹏程

(1.北京交通大学 交通运输学院， 北京 100044；2.北京交通大学 智慧高铁系统前沿科学中心， 北京 100044)

当高速铁路(以下简称“高铁”)列车偏离运行计划时，会给旅客带来诸多不便，尤其是对换乘旅客，晚点时间过长会导致这部分旅客不能正常换乘，更严重的是，当换乘列车为末班车时，旅客将被迫滞留而无法抵达目的地，造成列车服务的可达性降低。据统计，2020年换乘客流达3.4亿人次(换乘前后共2段行程)，当年旅客发送量21.67亿，总换乘客流占15.7%，对于较大的车站其换乘客流占比可能更多，如广州南站，平日换乘客流占全站发送量约20%，周末达到25%左右，小长假高峰换乘客流占全站发送量约30%[1]。因此，在干扰产生时科学合理地考虑旅客的换乘需求，并快速制定有效的列车运行调整方案是十分重要的。

近些年，关于列车运行调整问题国内外学者进行了深入的研究。张俊杰等[2]基于取消车次、延迟发车和降速运行3种策略建立了同时调整列车运行速度和运行图的模型，能够有效提高列车终到正点率。俞胜平等[3]提出了基于策略梯度强化学习的高铁列车动态调度方法，结合具体问题对Reinforce算法做了误差放大与阈值设定两种改进，能有效提高列车运行效率。王艺楠等[4]从微观层面把列车在路网上的运行抽象为对离散行车资源的占用，所构建的模型能在较短时间内提高调度应急处置能力。曾壹等[5]将该类问题转化为约束满足问题，围绕约束传递方法以及试错回退机制设计了一种具有高速计算特性的模型。李智等[6]将列车运行图的鲁棒性分为晚点传播鲁棒性与换乘接续鲁棒性，对两种鲁棒性进行多目标协同优化建模，该方法可有效提升高速铁路列车运行图的鲁棒性；李智等[7]结合智能CTC系统技术标准, 考虑动车组接续、交叉进路抵触及股道-线别连通性等关键信息，建立的多目标模型能够有效提高列车运行图调整的效果。徐培娟等[8]考虑初始晚点、限速和到发线不可用等多种行车干扰事件，建立兼顾车站进路的列车运行调整模型，可以快速求解得到列车变更到发线次数最少和列车晚点时间最短的列车调整方案。Altazin等[9]提出当突发事件造成的晚点时间较长时可以采用跳站停车的策略对列车运行计划进行调整，最终的决策取决于模型中多个目标线性加权的参数。Ghaemi等[10]在区间完全阻塞时采用临时折返策略对列车运行进行调整，明显提高了阻塞区间两侧的旅客服务质量。Veelenturf等[11]考虑旅客需求的变化对车底和运行图综合优化，提出的实时列车运行调整方法能极大地减少旅客的延误。Zhu等[12-13]提出一种将灵活停站、灵活折返等多种策略集成的列车运行实时调整模型，该模型能有效减少列车的总晚点时间，同时提升旅客的服务质量；并在此基础上首次提出了适用于多个突发事件同时发生时的列车运行动态调整模型，通过顺序和组合两种方法验证其有效性。Hong等[14]在列车因故障被取消时，构建列车运行图和列车停站计划一体化调整模型，通过增加后续列车停站的策略将受干扰的旅客运送至原计划目的地，但调整效果受限于后续列车的剩余载客能力。Zhang等[15]提出一种列车运行调整和轨道应急维护的实时协同优化策略，该策略不仅可以在线决定轨道的紧急维护，还可以处理干扰造成的延误，实现在线反馈校正的同时提高控制策略的鲁棒性。

综上，国内既有研究大多是以列车为导向，将特定的铁路运营指标如列车总晚点时间等作为目标函数，并不能真实体现列车运行调整对旅客服务质量产生的影响；国外既有研究虽然二者兼有考虑，但其具体的运营组织并不适用于我国高铁系统。

我国高铁现已成网运营，直达列车往往不能满足旅客全部的出行需求，旅客需要在枢纽站进行换乘。同时高铁作为计划型运输方式，旅客在出行前需实名制购票，客票包含旅客的行程、座席等信息。当列车发生晚点时，列车调度员可根据客票信息获得列车上换乘旅客数量及其换乘列车车次，对列车运行进行合理的调整。本文以此为背景，考虑干扰条件下不同运行线路的列车接续问题，同时兼顾列车时刻表与计划时刻表的偏离程度及其对换乘旅客造成的负面影响，在保证列车运行调整质量的同时提高客运的服务质量。

1 问题描述

本文以换乘旅客为重点研究对象，将旅客换乘前后乘坐的列车分别定义为前行列车和接续列车，旅客出行前购买前行列车和接续列车之间的接续时间不小于最小换乘走行时间的联程车票。为方便描述，假设线路1上有A、B、C 3个车站，线路2上有C、D 2个车站，C站为换乘站，旅客从A站出发前往D站，需要在C站进行一次换乘，若列车按计划运行，旅客可以进行换乘，如图1(a)所示。若接续列车在C站发生出发晚点，如图1(b)所示，前行列车与接续列车之间的实际接续时间会增加，满足最小的换乘走行时间，此时旅客可以成功换乘，本文不考虑这种情况；若前行列车在C站发生到达晚点，晚点时间较短时，如图1(c)所示，前行列车与接续列车之间的实际接续时间依然满足最小换乘走行时间，旅客仍可以换乘成功；若晚点时间较长，前行列车与接续列车之间的实际接续时间不再满足最小的换乘走行时间，旅客将无法换乘成功，此时如果合理改变接续列车的出发时刻，旅客就可以换乘成功，如图1(d)所示。因此，本文研究的核心思想是：当前行列车因干扰发生晚点时，合理调整前行列车和接续列车在各站的到发时刻，使路网中列车运行快速恢复到计划的同时让更多的换乘旅客成功换乘。

2 模型构建

2.1 问题假设

为了方便研究，作如下合理假设：

(1)故障发生前高铁列车严格按照计划时刻表运行，故障发生后故障区间能力完全失效，直到故障解除后列车才可以再次进入区间，并且故障持续时间已知。

(2)高铁线路上下行方向的行车组织互不干扰，本文假设其为两条独立的单向线路。

(3)各车站的到发线分上下行使用，数量固定且互不干扰。

(4)仅调整列车运行，不涉及动车组运用和乘务组的运用。

(5)旅客的客票数据是可获取，即每列车上换乘旅客的信息已知。假设前行列车和接续列车之间的换乘旅客的数量为1～20的随机整数。

2.2 符号设定及说明

本文通过控制列车在各车站的到发时刻来调整列车运行，相关的集合、参数符号及说明见表1，变量符号及说明见表2。

表1 集合、参数符号及说明

表2 变量符号及说明

2.3 模型建立

列车发生晚点时，列车晚点数、总晚点时间、终到晚点时间等指标可以评价一段时间内的运营情况，但却无法体现对旅客出行体验的影响，更无法准确衡量对换乘旅客的影响。对于换乘旅客来说，他们不仅关心晚点的时间，更关心是否可以成功换乘。本文将二者综合考虑：从列车角度出发，以调整后的列车时刻表与计划时刻表的偏离程度即所有列车的总晚点时间最小为目标，即

(ai,k,l-Ai,k,l)i∈Tlk∈Sll∈L

(1)

此目标考虑了所有列车在所有车站的实际到发时刻与计划到发时刻的差，期望降低干扰对高铁列车运营组织的影响。

从换乘旅客角度出发，以错过换乘旅客的数量即换乘失败的旅客数量最小为另外一个目标,即

∀i,j∈Tlk∈S*l,l′∈L

(2)

期望降低列车晚点对旅客出行体验的负面影响。

本文基于列车实际到发时刻的表达形式，将列车实际的运行组织和旅客换乘等规则建立以下约束，其中M是一个非常大的数。

(3)

式(3)为列车的停站约束。列车在计划停站方案中需停靠的车站在调整后也必须停站，保证计划的旅客乘降作业顺利进行。

∀i∈Tlk∈Sll∈L

(4)

式(4)为列车的停站时间约束。若停站，列车在车站的停站时间应不小于最小停站时间；若不停站，则列车在该站的实际到站时刻与实际出发时刻相等。

si,k,l·τt∀i∈Tlk∈Sll∈L

(5)

式(5)为列车的区间运行时分约束。列车在两站之间的区间运行时分不能小于列车在此区间的最小纯运行时分与起停附加时分之和。

dj,k,l-di,k,l≥h-M·(1-xi,j,k,l)

∀i,j∈Tlk∈Sll∈L

(6)

aj,k,l-ai,k,l≥h-M·(1-xi,j,k-1,l)

∀i,j∈Tlk∈Sll∈L

(7)

xi,j,k,l+xj,i,k,l=1 ∀i,j∈Tlk∈Sll∈L

(8)

式(6)～式(8)为列车运行间隔约束，同时也表示列车在车站的越行约束。式(6)表示同一线路上运行的两列列车在同一车站的实际出发时刻之间的间隔需要满足列车最小追踪间隔时间；式(7)表示同一线路上运行的两列列车在同一车站的实际到达时刻之间的间隔需要满足列车最小追踪间隔时间；同时，式(6)和式(7)共同保证列车只能在车站发生越行；式(8)保证两列列车先后顺序的唯一性。

(9)

aj,k,l-di,k,l≥H-M·(1-xj,i,k,l-zi,k,p-zj,k,p)

∀i,j∈Tlk∈Slp∈Pkl∈L

(10)

ai,k,l-dj,k,l≥H-M·(1-xi,j,k,l-zi,k,p-zj,k,p)

∀i,j∈Tlk∈Slp∈Pkl∈L

(11)

式(9)～式(11)表示列车在车站占用到发线的约束。式(9)保证一列列车在一个车站最多只允许占用一条到发线；式(10)和式(11)表示同一线路的两列列车在同一车站占用同一到发线时，前方列车的实际出发时刻与后方列车的实际到达时刻之间的间隔应不小于最小到发间隔。

∀i,j∈Tlk∈Slk′∈S*l,l′∈L

(12)

式(12)为旅客换乘接续约束。旅客在换乘站能够成功换乘时，旅客将乘坐的接续列车在该站的实际出发时刻与前行列车实际到达该站的时刻之间的间隔应大于等于旅客在该站的最小换乘走行时间。

∀i∈Tlk∈Sll∈L

(13)

∀i∈Tlk∈Sll∈L

(14)

式(13)和式(14)为与突发故障有关的约束。突发故障开始之前，列车严格按原计划运行，在各站的实际出发和到达时刻与计划出发和到达时刻相等；突发故障开始之后、结束之前，列车禁止进入故障发生区间；突发故障解除之后，列车在车站的实际出发时刻不能早于计划出发时刻。

2.4 求解方法

目标式(1)和式(2)及约束式(3)～式(15)所表示的模型是一个双目标模型，此类多目标模型无法直接求解，一般将多目标转化为单目标后进行间接求解。ε约束法(ε-Constraint Method)相比于其他求解多目标问题的方法，无需设置额外的权重系数，更无需考虑不同目标之间的量纲和数量级，能够方便快速的求解，本文采用该方法。

从换乘旅客的角度出发，将目标2即换乘失败的旅客数量最小作为最终目标，选择目标1即所有列车总晚点时间最小作为ε约束，将式(1)转化为式(15)并加入到模型中。

∀i∈Tlk∈Sll∈L

(15)

通过不断地以Δε为粒度更新容忍度ε，重复对目标式(2)求解最优值，可以获得一组近似Pareto最优解。需要注意的是，求解过程中可能会出现某一个容忍度ε更新为ε′后，以目标式(2)求解的最优值保持不变，但对应多个可行的目标式(1)，这是因为对目标式(1)的松弛不够大，不足以使目标式(2)进一步优化，此时仍选取容忍度为ε时的解为最优的解决方案。

3 案例分析

3.1 案例描述

本文选取京沪高铁北京南—徐州东区段下行方向和胶济客运专线济南西—青岛北区段下行方向构成的路网为案例进行研究，该路网站点分布见图2，其中济南西站为旅客换乘的枢纽站。将北京南到徐州东下行方向看做延误线路，全线共11个车站、 10个区间，从7:40—10:10于北京南站发出20列列车；将济南西到青岛北看做接续线路，全线共7个车站、6个区间，从9:40—13:00于济南西发出(或途径)15列列车。需要说明的是，本文所建立的模型对于路网更复杂、规模更庞大的案例也是适用的。

图2 北京南—徐州东区段和济南西—青岛北区段站点分布示意图

根据实际情况，模型中涉及的参数设置如下：起车附加时分为2 min，停车附加时分为3 min，列车追踪间隔时间和到发间隔时间为3 min，最小停站时间为2 min，根据济南西高铁站的站内结构，旅客在换乘站的最小换乘走行时间设置为15 min，根据2.1节中的假设5得到路网中换乘旅客数量，见表3，各线路车站到发线的数量、区间最大、最小纯运行时分及区间距离见表4、表5，M取1 440。

表3 路网中旅客换乘矩阵

表4 北京南—徐州东区段车站到发线数量、下行方向区间纯运行时分及区间距离

表5 济南西—青岛北区段车站到发线数量、下行方向区间纯运行时分及区间距离

3.2 结果分析

本文所构建的模型在CPU型号为 Inter(R) Core(TM)i5-10600KF 4.10 GHz，内存16 GB 的计算机上使用标准求解器Gurobi 9.1.1进行求解，所有研究的案例均在100 s内得到最优解。

3.2.1 近似Pareto最优分析

假设在延误线路中，天津南到沧州西的区间于9：05发生突发故障，故障持续25 min，故障期间禁止列车进入区间，根据此假设对案例进行求解来验证模型和求解方法的可行性和有效性。

从列车角度出发，先以目标式(1)对所构建的模型进行求解，即ε=0时，不考虑旅客换乘时调整后的列车运行图，见图3。由图3(a)可知，故障导致延误线路有三列列车在天津南站被迫停车等待，两列列车在廊坊站被迫停车等待，故障解除后列车开始恢复行车，这种情况下得到的调整方案仅对延误线路的列车进行了调整，没有考虑列车晚点对换乘旅客的影响，接续线路的列车仍按计划运行图运行。图3(b)中调整后的列车运行线与计划运行线重叠，这种情况得到的解决方案与实际中列车调度员采用的“赶点”方法类似。

将容忍度ε更新为0.1求解并与ε=0时的解决方案进行对比，两种方案下运行图的对比见图4，可以看出，ε=0.1时的调整方案在延误线路只是相较于ε=0时的调整方案进行了微小调整，但为了保证更多的旅客可以成功换乘，使接续线路中的部分列车在济南西站晚点发车，同时也通过改变列车在区间的运行时间保证列车能正点到达终点站。

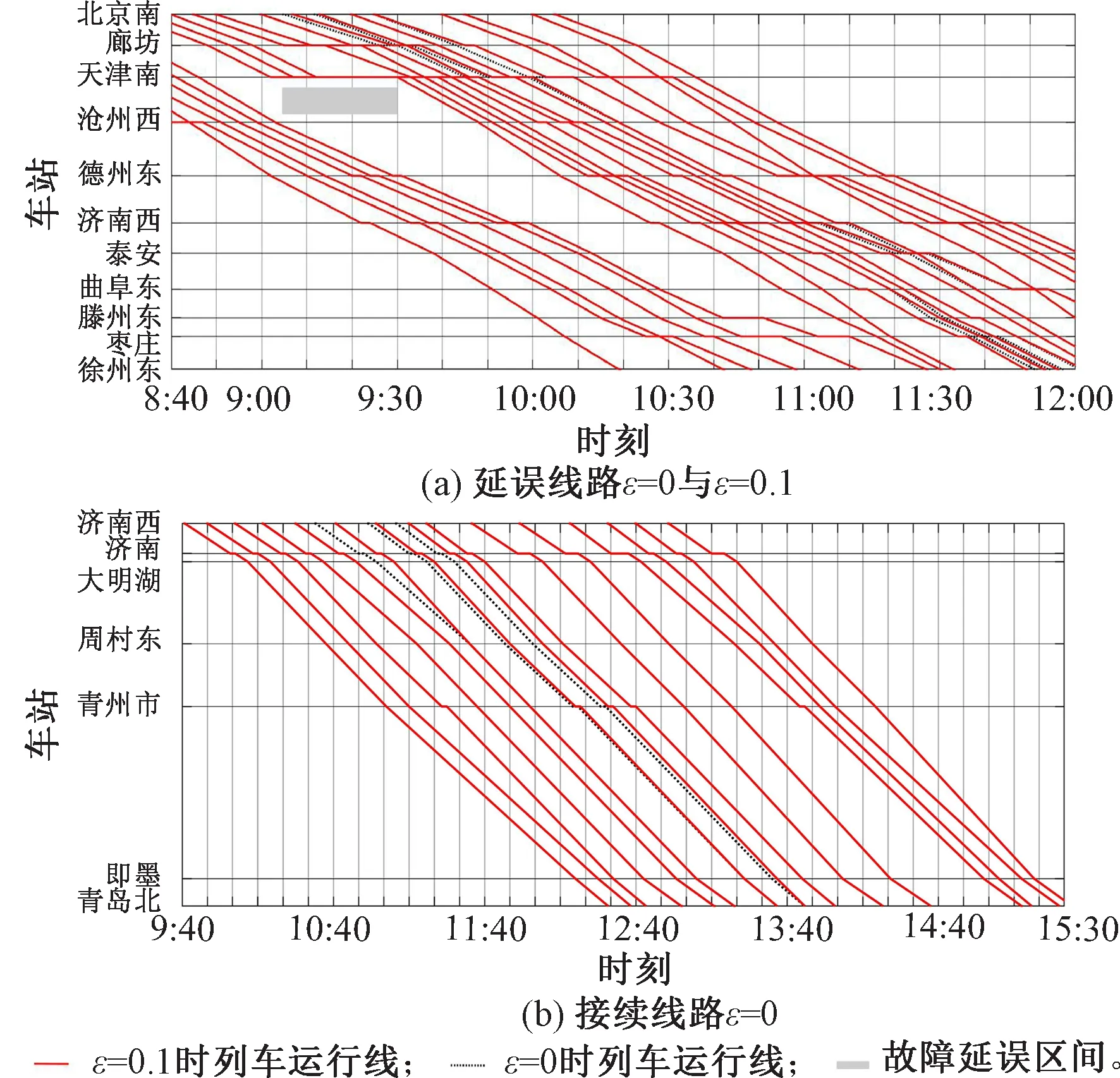
图4 调整方案的对比

由表6中两种方案的目标值及相关信息可以得到，以ε=0.1时求解得到的调整方案虽然导致列车总晚点时间增加了8.99%，列车在终点站的总晚点时间增加了1.25%，终点站晚点列车数保持不变，使换乘失败的旅客人数降低了61.36%。由此看出本文所构建的模型可通过损失一定程度的列车运行恢复时间，使路网中换乘失败旅客数量明显下降，在列车发生晚点时能够使更多乘客完成换乘，显著提升客运服务质量。

表6 不同ε取值时的求解结果

在上述两种方案的基础上，从ε=0开始，以Δε=0.05为间隔对ε的取值更新，重复对该场景求解计算可以得到一组不同方案下的近似Pareto解，每种方案下的列车总晚点时间和换乘失败旅客数量的变化趋势见图5。

根据图5可以发现，随着对列车总晚点时间容忍度ε的不断增大，换乘失败的旅客数量在迅速下降，而列车总晚点时间则渐渐增大，反映了所构建模型中的两个目标之间在相互制约、相互影响。但列车总晚点时间在近似呈线性增加的过程中，换乘失败旅客数量的下降幅度在逐步变小，说明列车总晚点时间增大的边际效用是递减的。当ε= 0.35时，换乘失败的旅客数量下降到0，说明在以35%为上限对列车总晚点时间进行松弛时，就可以让所有的旅客换乘成功。在列车实际运营时，列车调度人员是不允许列车调整后的时刻表与计划时刻表之间的偏差无限扩大的，本文所做的研究能够快速提供一组可行有效的列车运行调整方案，可供调度人员评估故障发生后的具体情况选择一个最优方案。

图5 不同方案下目标值的变化趋势

注：列车在终点站平均晚点时间=列车在终点站总晚点时间/终点站晚点列车数量，↑代表增加，↓代表下降，—代表无变化，下文相同。

3.2.2 不同故障场景适用性分析

根据故障类型及其发生的时间和位置重新设置三种故障场景，场景1是于9：05在天津南至沧州西的区间发生故障，故障解除前任何列车禁止进入该区间；场景2是计划于9：22在德州东站出发的列车因故障被迫停留在车站造成出发晚点，故障解除前该列车占用一条到发线；场景3是计划于上午9：29到达德州东站的列车因故障在沧州西到德州东的区间上被迫降速或停车，造成该列车在德州东站到达晚点。每种场景又根据故障持续时间的不同分别设置15、25、35 min 3种情况。对上述3种场景共9种情况分别进行求解，求解结果如表7所示。

分析表7可以看出，当故障持续时间增加时，上述3种故障场景下的列车总晚点时间和换乘失败旅客数量也会增加，这是因为在列车实际运行过程中，一列列车晚点时间越长，对后续列车造成的连带晚点也会越多，不仅会导致所有列车总晚点时间增加，更会导致越多的旅客无法成功换乘。对列车总晚点时间以10.00%为上限进行松弛，即设置ε=0.1时，虽然会使列车总晚点时间有所增加，但换乘失败旅客的数量均大幅下降，下降最少为12.50%，最多可高达88.23%。

从表7中ε=0和ε=0.1两种设置的计算结果来看，增加一定程度的列车总晚点时间能显著降低换乘失败旅客的数量，调度人员可根据具体的突发故障场景，通过设置合理的ε取值来选取一个兼顾列车运行和旅客服务水平的最优调整方案。由此表明，本文所构建的模型能够较好地适用于各种突发故障的场景，为调度人员进行调度决策提供合理可行的参考。

表7 不同故障情景下各种情况的求解结果

4 结束语

本文在高速铁路成网运营条件下，考虑列车运行干扰对旅客换乘造成的影响对高铁列车运行进行调整，以列车总晚点时间最小和未成功换乘的旅客人数最小作为目标，综合考虑行车秩序和旅客换乘衔接等约束构建了混合整数线性规划模型，并使用ε约束法求解计算。以京沪高铁部分区段和胶济客运专线部分区段所构成路网的实际数据为基础，对具体故障场景进行近似Pareto最优分析和不同干扰场景的适用性等进行测试，结果表明本文所构建的模型能够快速地获得一组兼顾列车系统和旅客服务水平的列车运行调整方案，可为调度人员提供辅助决策。

本文是在仅考虑一个突发事件且故障持续时间已知的前提下对高铁列车运行调整进行研究的，考虑到突发事件的随机性和不确定性，将本文构建的模型扩展到在高铁路网内同时发生多个突发事件且持续时间不确定情况下的列车运行调整问题是下一步研究的重点。