取舍有道 融合有度
吴永庆
【摘 要】珠心算训练可以提升学生的计算能力、视觉空间和逻辑推理能力,提高学生认知的灵活性,强化学生解决问题的能力,增强学生大脑的可塑性,加强左右脑之间信息的快速交互,促进学生大脑的发展。在珠心算与传统数学融合的实验教学中,由于教学时间和训练时间安排、传统数学和珠心算教材不匹配、两者之间的计算算理偏差等问题,二者未能很好结合,难以产生效果。本文试图以具体内容为例,谈谈珠心算与传统数学课程融合的一些做法。
【关键词】珠心算 数学 融合
浙江大学物理系交叉学科实验室陈飞燕教授曾做过珠心算课题研究,其研究表明:珠心算训练能够大幅度提升儿童的计算能力,促进儿童数字敏感性和数字认知的发展,显著提升儿童的数学视觉空间和逻辑推理能力,同时提升和优化脑网络,促进儿童大脑的发展。
基于珠心算的这些优势,越来越多的团体机构、学校加入珠心算的实验教学中。对于学校而言,要在原本课程设置比较完善且充足的情况下增加珠心算的教学,无形中就在课时分配和教学任务方面增加了难度。如何解决这个问题?自然是课程融合!将数学与珠心算进行融合,但是融合时又会带来新的问题,比如教材互不匹配、計算时算理不完全一致等,这些都需要教师在日常教学中一一破难解决。本文将以数学教材中“9加几”和珠心算教材中“加9的进位加(1)”融合为例,谈谈实际教学中如何破解融合难题。
“9加几”是数学一年级上册“20以内的进位加法”单元的第一课时,“加9的进位加(1)”是珠心算第一册“20以内的进位加法”单元的第一课时,从内容上看两者比较相似,所以这给融合教学带来了可能;从教学要求上看,“9加几”是引导学生依靠已有经验,借助直观辅助,理解“凑十法”的计算思路;“加9的进位加(1)”是让学生理解加9的进位加基本算理“减1进1”,同时在指法上,学生首次接触左右手同时使用。乍一看,这节课的融合难度不大,因为内容相似甚至完全相同,基本不会有什么困难,但是实际操作时却会发现很多问题。
问题1:课题匹配,教材内容不匹配。
从课题来看都是跟9有关的进位加法,但是“9加几”和“加9的进位加(1)”又是有明显区别的,前者9做被加数,后者9做加数。
问题2:计算算理和珠心算算理存在区别。
“9加几”的基本算理是“凑十法”,这其中有“拆小数、凑大数”和“拆大数、凑小数”两种,不管是哪一种都是“加”的思维;“加9的进位加(1)”的基本算理虽然也是“凑十法”,但基本口诀是“减1进1”,在口诀上用的是“减”的思维。
根据以上分析,笔者认为,两者如果需要融合教学,一是需要进行教材内容的融合,要既能适应“9加几”的教学,又能适应“加9的进位加(1)”的教学;二是要对算理部分的教学进行深度研究,使学生对算理的理解过程在头脑中能清晰呈现且过渡自然。
一、斟酌取舍巧引入,教材一致易教学
“9加几”的教材内容是借助情境图,以“9+4”作为主算式进行教学,引导算理讨论最终获得基本算理;“加9 的进位加(1)”的教材内容同样是借助情境图,却是以“3+9”作为主算式进行教学,引导算理讨论最终获得基本口诀。从算式上看,9的位置是最大的区别。从安排思路上看,9的位置其实就是两种教材的重点所在,“9加几”重点在“凑十法”,引导学生“拆小数、凑大数”,所以将大数“9”放左边作为需要凑满10的数,被拆的数放右边,给9随时提供凑满10的1,这样的安排可以让学生思维的指向性更加准确。“加9的进位加(1)”作为珠心算的教学内容,必须遵循珠心算程序化计算模块,根据出现的数选择口诀,并依据口诀进行拨珠计算。这节课中口诀都是“减1进1”,也就是说后出现的数必须是“9”,前面的数则是随机选择,算式都是“x+9”。
综合上面的分析,考虑到珠心算的程序化计算模块,9的位置不能改变,同时数学中“9加几”内容只是为了新授时使学生更加容易接受“拆小数、凑大数”的基本算理,将“9加几”变更为“几加9”并不影响学生对“拆小数、凑大数”的算理理解,所以在教学内容的选择上做出取舍,统一使用9在右边的算式形式,并配套更改情境图,便于学生直观思考,理解算理。
二、化异为同妙设计,算理一致易融合
“9加几”和“加9的进位加(1)”的算理思维,其中一种是“加”的思维,另一种是“减”的思维,但究其根本,二者的算理都是使用“凑十法”的基本原理,而且都主张“拆小数、凑大数”,属于同源算理。那么,在教学设计时,教师可以根据同源算理进行巧妙勾连,借助课件和语言引导,将两种思维进行整合互通,转化成同一种思维方式帮助学生理解算理,使得两种教材的不同计算路径得以有效融合。
【教学设计】
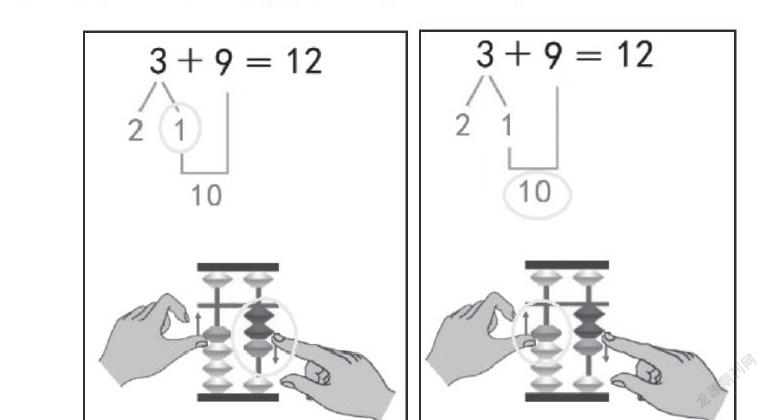
出示算理对比情境图(如下图)。
3分成1和2,9和1凑成10,10和2合成12,结果是12。
师:我们一起来看看“3+9”是怎么算出来的。
生:要先把大数9凑成10,就要把3分成1和2。
师:是的,3分成1和2,9和1凑成10,那这里的1是为了给9凑成10的,从3里面分出去了,相当于是3减去1,所以在算盘上就是“减1”。
生:再把凑成的10和剩下的2合起来是12。
师:说得很好,凑成的10在算盘上应该在什么位置呢?
生: 10应该在十位,用1颗下珠表示。
师: 是的,用十位上1颗下珠表示10,口诀是“进1”。
师:这样连起来就是3分成1和2,9和1凑成10,10和2合成12,结果是12。跟着老师一起说。
学生边拨珠边说(分组说、个别说、同桌互说)……
这样的引导梳理和融汇训练,帮助学生建立起两种不同思维之间算理的融通之处,排除学生因为算理不同带来的干扰因素,使无论是“9加几”的教学要求还是珠心算“加9的进位加(1)”的教学要求都得以达成。同时也为学生口算能力的提升打下了坚实的基础,如思考“9+4”时,学生可以很自然地利用“减”的思维,原本的完整思维是“4分成1和3,9和1凑成10,10和3合成13,结果是13”,利用“减”的思维,学生可以直接这样思考:“4减1剩3(凑10),10和3合成13”。这样就减少了口算算理的中间烦琐环节,提高了口算的效率,不仅为数学计算的后续教学打下良好的基础,同时也为学生进一步学习珠心算,并将珠心算用于实际习题操作提供了重要保证,这样就不再是珠心算和数学计算两条线,而是合二为一,效率更高,效果更好。
珠心算主要针对的是数学中的计算类别,所以在融合实验时也是针对数学中计算的融合,珠心算的算理和口诀与数学计算中的算理和口诀虽然存在区别,教材内容的编排上也有出入,但是其数学计算的基本学习顺序和基本算理上是一致的,实验教师只要做有心人,认真研究两本教材,就会找到二者之间的融通之处,将珠心算的教学和数学的计算教学有机融合起来,形成合力,帮助学生提升计算能力,同时促进学生对于数字的敏感性以及数字认知的发展,培养学生数学视觉空间观念和逻辑推理能力。

