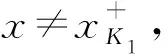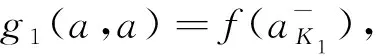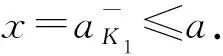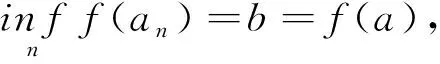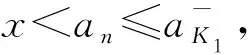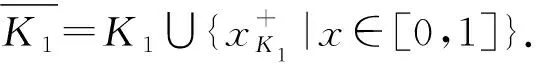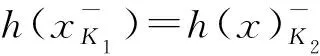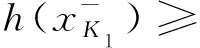单位区间上由Gödel模和Galois联络生成的三角模

孙 杰, 张德学

(四川大学 数学学院, 四川 成都 610064)

三角模在模糊逻辑[1-2]、函数方程[3]等领域中有很重要的作用,它的结构与构造方法得到了广泛的研究,系统的总结和论述参见文献[3-4].利用Galois联络构造三角模是一种很有效的方法,例如连续的阿基米德模就是由单位区间上的乘积模和一类特殊的Galois联络生成的三角模.具体地说,二元运算T:[0,1]2→[0,1]是连续的阿基米德模当且仅当存在严格递增的连续函数g:[0,1]→[0,1]使得g(1)=1并且

T(x,y)=g(-1)(g(x)·g(y)),

其中g(-1)是g的伪逆,即

g(-1)(x)=min{y|x≤g(y)}=

详见文献[3]的定理2.2.1.注意到此时伪逆g(-1)就是g的左伴,文献[5]指出可以利用Galois联络构造偏序集上的三角模(定义见文献[6]或定义1.4),并证明了以下结论.

定理 1.1设P、Q是有最大元和最小元的偏序集,d:P→Q和g:Q→P是保序映射并且d是g的左伴.若T是P上的三角模且对任意x,y∈Q恒有

T(g(x),g(y))∈g(Q)∪{ω∈P|ω≤g(0)},

则Tg是Q上的三角模,其中

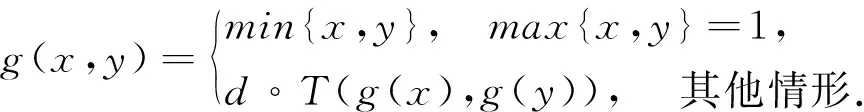
设P=Q=[0,1],d┤g:[0,1]→[0,1]是Galois联络,T是[0,1]上的Gödel模(也称取小模),即T(x,y)=min{x,y}.则条件

T(g(x),g(y))∈g(Q)∪{ω∈P|ω≤g(0)}

恒成立,于是由定理1.1得

Tg(x,y)=

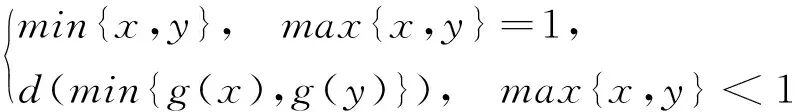
是[0,1]上的三角模,称为由Gödel模和Galois联络d┤g生成的三角模.本文研究了这类三角模的结构,给出了完整的刻画,证明了两个这样的三角模同构当且仅当彼此的幂等元集之间存在保序同胚.

1 预备知识

这一节简要回顾本文将用到的Galois联络的基本性质以及偏序集上三角模的定义.单位区间上(连续、左连续)三角模的概念和基本性质请参考文献[3-4].

定义 1.1[7]设P和Q是偏序集,d:P→Q和g:Q→P是保序映射.若对任意p∈P,q∈Q都有d(p)≤q⟺p≤g(q),则称d是g的左伴,g是d的右伴.此时称(d,g)为一对Galois联络,记作d┤g:Q→P或d┤g.

定理 1.2[7]设d:P→Q和g:Q→P是偏序集之间的保序映射,则下列条件等价:

1)d┤g;

2)dg≤1Q且1P≤gd;

3) ∀x∈P,d(x)=min{y∈Q|x≤g(y)};

4) ∀x∈Q,g(y)=max{x∈P|d(x)≤y}.

定理 1.3[7]设g:P→Q是保序映射并且P是完备格.则g保下确界当且仅当g有左伴.特别的,保序映射g:[0,1]→[0,1]有左伴等价于g右连续且g(1)=1.

定义 1.4[6]设P是有最大元1的偏序集.称二元运算T:P×P→P是P上的三角模若T在每个分量上保序且满足下列条件:

(T1)T(x,y)=T(y,x);

(T2)T(1,x)=T(x,1)=x;

(T3)T(T(x,y),z)=T(x,T(y,z)).

若T是偏序集P上的三角模,则(P,T)是以1为单位元的幺半群.设T是偏序集P上的三角模,S是偏序集Q上的三角模.称T与S同构若存在序同构f:P→Q使得任给x,y∈P,f∘T(x,y)=S(f(x),f(y)).

2 主要结论

除非另外声明,总是假设d┤g:[0,1]→[0,1]是Galois联络,Tg表示由Gödel模和d┤g生成的三角模,即

Tg(x,y)=

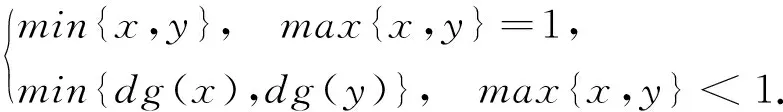
称单位区间[0,1]的子集K关于上确界封闭若任给A⊆K恒有∨A∈K.特别的,0=∨∅∈K.

引理 2.1设K⊆[0,1]关于上确界封闭.任给x∈[0,1],令

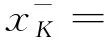
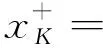
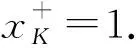
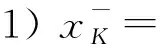
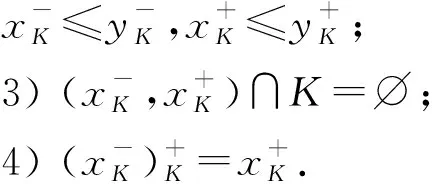
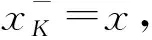
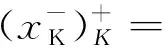
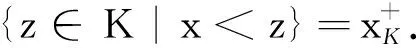
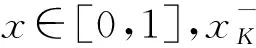
定理 2.2设K是Tg的幂等元集,即K={x∈[0,1]|Tg(x,x)=x}.则:

1)K={dg(x)|x∈[0,1]}∪{1};

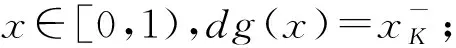
3) 任给x,y∈[0,1),Tg(x,y)=min

证明1) 由Tg的定义,

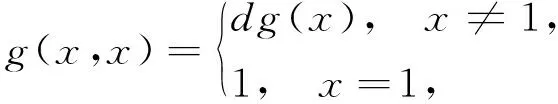
于是

K={x∈[0,1]|Tg(x,x)=x}=

{x∈[0,1]|dg(x)=x}∪{1}.

(1)

又因为任给x∈[0,1],dgdg(x)=dg(x),所以K={dg(x)|x∈[0,1]}∪{1}.

2) 为了说明K关于上确界封闭只需证明任给A⊆K{1},supA∈K.若A=∅则supA=0∈K;若A≠∅,则由(1)式知对任意的x∈A都有x=dg(x),于是A=dg(A).因为

supA=supdg(A)≤dg(supA)≤supA,

3) 由Tg的定义和2)直接可得.

推论 2.3设K是Tg的幂等元之集.则下列各条等价:

1)Tg=min;

2)Tg连续;

3)Tg左连续;

4)K=[0,1].

证明只需证明3)⟹4)⟹1).

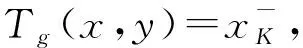
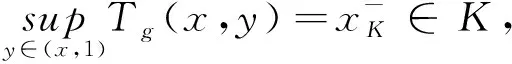
从而K=[0,1].

4)⟹1) 任给x,y<1,由定理2.2的3)可得

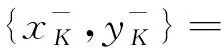
于是Tg=min.

由定理2.2知由Gödel模和Galois联络生成的三角模的幂等元集包含1且关于上确界封闭,下面的定理表明反过来结论也成立.

定理 2.4设K是单位区间[0,1]关于上确界封闭的子集并且包含1,则存在Galois联络d┤g:[0,1]→[0,1]使得K是三角模Tg的幂等元集.

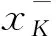
由引理2.1的4)可得任给x∈[0,1],g(x)=g(x-).下面说明g有左伴,设为d:[0,1]→[0,1],并且Galois联络d┤g满足条件.

第一步g单调递增.说明g在K上的限制严格递增.设x,y∈K且x

第二步g右连续,于是有左伴.任给0≤x<1,分2种情形讨论.

情形 1x=x+.由g的定义易知此时g(x)=x.由x+的定义知存在K中严格递减的序列{an}n收敛于x.因为对任意n≥1都有

所以{g(an)}n收敛于x(=g(x)).利用g的单调性以及limg(an)=g(x)可得g在x处右连续.

情形 2x

第三步K是Tg的幂等元之集,即K={dg(x)|x∈[0,1]}∪{1},其中d是g的左伴.由于K={x-|x∈[0,1]},说明任给x∈[0,1],dg(x)=x-即可.

由定理1.2的3),dg(x)=min{t∈[0,1]|g(t)≥g(x)}.一方面,由g(x-)=g(x)可得dg(x)≤x-.另一方面,任给y

定理2.2的3)表明由Gödel模和Galois联络生成的三角模可由它的幂等元集确定,因此这样的三角模可以通过它们的幂等元集来分类,这就是下面的结论.

定理 2.5设di┤gi:[0,1]→[0,1]是Galois联络,Ki是三角模Tgi的幂等元之集,i=1,2.则下列各条等价:

1) 三角模Tg1与Tg2同构,这等价于存在保序的双射h:[0,1]→[0,1]使得h∘Tg1=Tg2∘(h×h);

2) 幺半群([0,1],Tg1)与幺半群([0,1],Tg2)同构;

3) 存在K1到K2的保序同胚.

证明1)⟹2) 显然.

2)⟹3) 设f:([0,1],Tg1)→([0,1],Tg2)是幺半群同构.下面说明f在K1上的限制是K1到K2的保序的同胚.

首先,由于f:([0,1],Tg1)→([0,1],Tg2)是幺半群同构,K1和K2分别是两个幺半群的幂等元之集,故f在K1上的限制f|K1是K1到K2的双射.

其次说明f|K1:K1→K2保序.若不然,则存在x,y∈K1满足xf(y),于是

Tg2(f(x),f(y))≤f(y)

与f同构矛盾.

同理可知f|K1的逆映射也连续,于是f|K1:K1→K2是保序同胚映射.

h(x)=