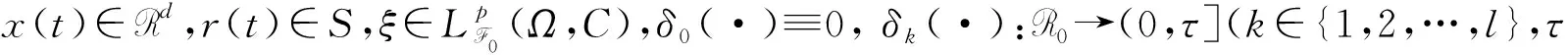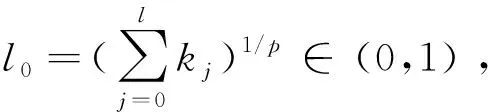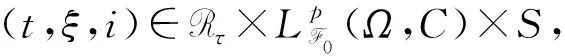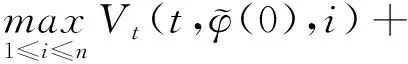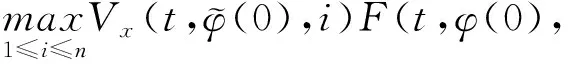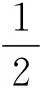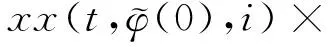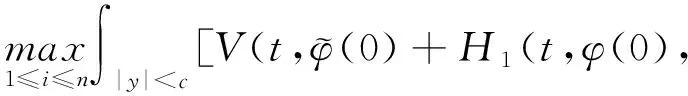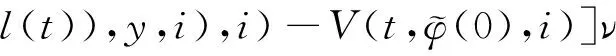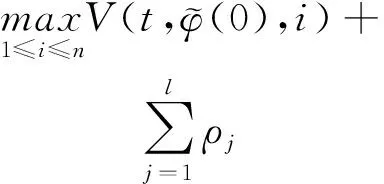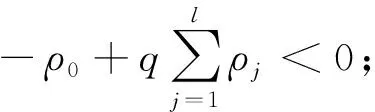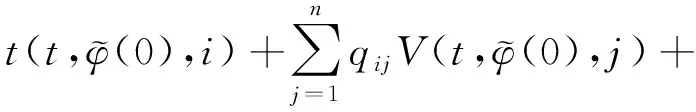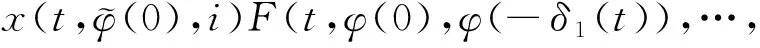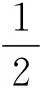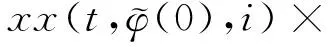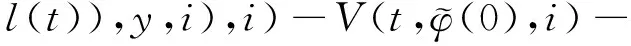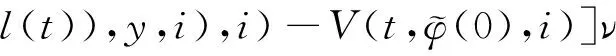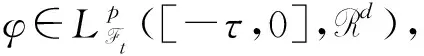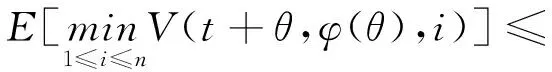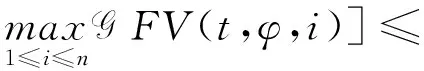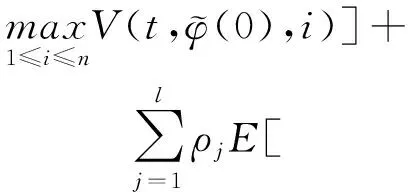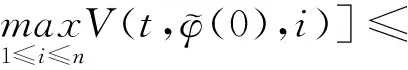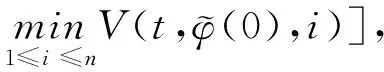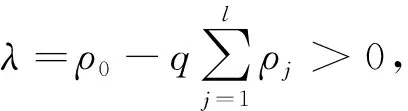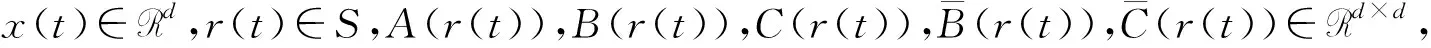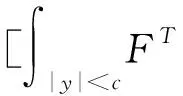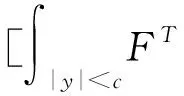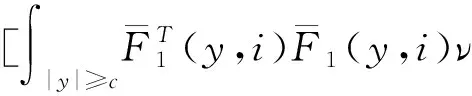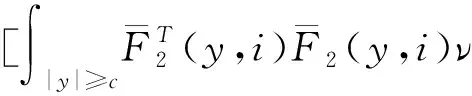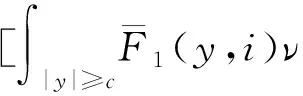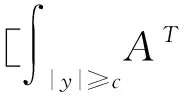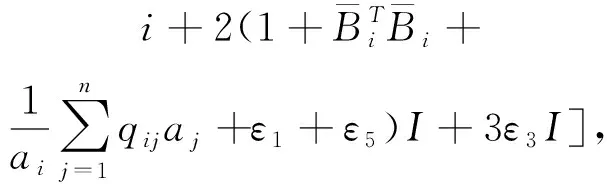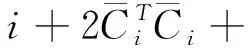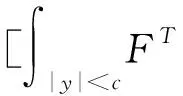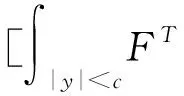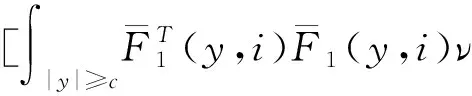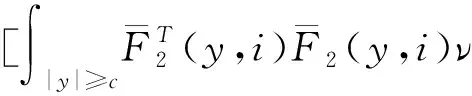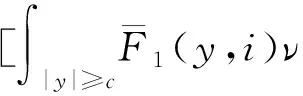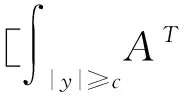具Markov切换和Lévy噪声的中立型随机泛函微分方程p阶矩指数稳定性
肖 可, 李树勇
(1. 四川轻化工大学 数学与统计学院, 四川 自贡 643000; 2. 绵阳师范学院, 四川 绵阳 621000)
近几十年来,由于在自然科学、生物工程、医学、金融等各个领域的应用,中立型随机泛函微分方程稳定性被学者们广泛关注,建立了一系列判别中立型随机泛函微分方程解稳定性的结果[1-8]. 然而,一个实际的系统常不免有多种随机因素的介入,Markov切换是一种常见的随机干扰,由于其样本路径的不连续性,Markov切换对随机微分系统有极大影响,往往会导致系统的不稳定.文献[6]研究了一类具Markov切换的中立型随机泛函微分方程解的指数稳定性,利用Razumikhin方法,建立该系统的Razumikhin型稳定性定理,分析了Markov切换对该系统稳定性影响;文献[7]研究了一类具Markov切换的中立型随机泛函微分方程解的指数稳定性,通过构造恰当的Lyapunov泛函,并结合随机分析理论及不等式技巧,建立了该系统解p阶矩指数稳定与几乎处处指数稳定的充分条件,克服了样本路径不连续性对稳定性的影响.此外,Brownian运动作为一种连续的随机过程不能较好地表述那些服从随机突变的实际系统,而对于随机突变造成的不连续现象,Lévy噪声可以更好地刻画这种随机突变.因而,具Lévy噪声的中立型随机泛函微分方程解的稳定性问题受到学者们重视,文献[8]研究了一类具Lévy噪声的中立型随机泛函微分方程解的稳定性,通过构造恰当的Lyapunov泛函,并结合随机分析理论与不等式技巧,得到该系统解p阶矩渐近稳定与几乎处处渐近稳定的充分条件.在实际应用中,Markov切换与随机突变往往同时存在,具Markov切换和Lévy噪声的随机泛函微分方程反映了这种现象.但由于样本轨道不连续,且Markov切换和Lévy噪声同时存在,稳定性分析面临更多困难,据我们所知,相关问题研究尚不多见.最近,文献[9]将Razumikhin方法应用到具Markov切换和Lévy噪声的随机泛函微分方程解的稳定性研究上,克服了这一困难,建立了具Markov切换和Lévy噪声的随机泛函微分方程解的p阶矩指数稳定性判别定理.受此启发,本文将研究具Markov切换与Lévy噪声的中立型随机泛函微分方程解的稳定性,通过使用Razumikhin方法,并结合随机分析理论以及不等式技巧,建立该系统解p阶矩指数稳定的充分条件,进而得到具Markov切换和Lévy噪声的中立型随机时滞微分方程解的p阶矩指数稳定性判别定理.
1 预备知识
本文|x|表示向量x∈d的欧式范数,w=(w1(t),w2(t)…,wm(t))T(t≥0)是一个m维标准Brownian运动.对非负常数τ,记
τ=[-τ,+∞), CC([-τ,0),d),
C依范数
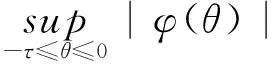
成为一个Banach空间.对每一个C值随机变量φ(θ,ω),约定
Lpt(Ω,C)={φ:φ是t可测的C值随机变量,
E‖φ‖p<∞},
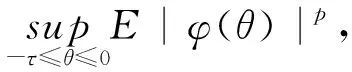
这里E表示关于所给概率测度P的期望.
设{r(t),t≥0}是在完备概率空间(Ω,,P)上的一个右连续Markov链,并且取值于有限状态空间S={1,2,…,n}(n表示正整数),其中生成元Q=(qij)n×n满足条件:
P{r(t+Δt)=j|r(t)=i}=
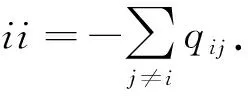
r(t)=r(τk), ∀t∈[τk,τk+1),k∈N.
设N是定义在0×(d{0})上的一个泊松随机测度,是N的补偿泊松随机测度,并且与Brownian运动w(·)相互独立,这里ν是一个Lévy测度,并且有
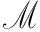
考虑如下具Markov切换和Lévy噪声的中立型随机泛函微分方程:
d[x(t)-D(t,xt,r(t))]=f(t,xt,r(t))dt+
g(t,xt,r(t))dw(t)+
(1)
其中,x(t)∈d,xtxt(θ)={x(t+θ):-τ≤θ≤0}为一个C值随机过程,xt-且xt-∈C,函数D:0×C×S→d,f:0×C×S→d,g:0×C×S →d,m和h1,h2:0×C×d×S →d,并满足后面所需条件,常数c∈(0,+∞]为允许的最大跳跃高度,假定r(t)=i取遍S而不处处注明.
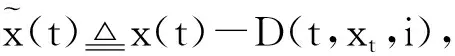

|D(t,φ1,i)-D(t,φ2,i)|≤κ‖φ1-φ2‖.(2)
(A2) 对任意的k=1,2,3,…,存在lk>0使得
|f(t,φ1,i)-f(t,φ2,i)|2∨
lk‖φ1-φ2‖2,
(3)
对任意的t≥0,以及φ1,φ2∈C,且‖φ1‖∨‖φ2‖≤k成立.
(A3) 存在一个常数l >0,使得
对任意的φ∈C以及t≥0成立.
(A4) 对任意的t≥0,有:D(t,0,i)≡0,f(t,0,i)≡0,g(t,0,i)≡0,且对|y| 记方程(1)满足初值x0=ξ的解为x(t;ξ)(也记为x(t)).显然,对任意的t≥0,方程(1)有零解x(t)=0. 记C1,2(τ×d×S)为定义在τ×d×S上的所有非负函数V(t,x,i)的集合,并且V对t为一阶连续可微的函数,对x为二阶连续可微的函数.对于任意的φ∈C以及t∈τ,约定对于任给的V ∈C1,2(τ×d×S)以及φ∈C,定义V:τ×d×S→如下. (5) 这里 E|x(t;ξ)|p≤α‖ξ‖p0e-βt, ∀t≥-τ, 则称方程(1)的解p阶矩指数稳定. 证明不妨设T>0适当小,使得 其中D2=为正常数;L=(显然L>0).固定初值ξ,定义Picard迭代序列如下: (6) 首先验证{xn(t)}定义合理、连续,且xn(t)∈2([0,T];d). 这与文献[5]定理3.1.2之证类似,从略. 接着证明{xn(t)}在空间2([0,T];d)中范数收敛.为此,只要归纳地证明以下不等式: bδn,n≥0, (7) b=bδ0. 今设Mn-1≤bδn-1(n≥1),则 h2(s,xn-1s-,y,r(s))]N(ds,dy)|2}≤ h1(s,xn-1s-,y,r(s))|2ν(dy)ds]+ h2(s,xn-1s-,y,r(s))|2ν(dy)ds]≤ 故(7)式得证.由(7)式推出{xn(t)}是2([0,T];d)中的Cauchy序列,故其范数收敛于某个x(t)∈2([0,T];d). 于是由Borel-Cantelli引理推出,a.s.地,有 推出所要结论.从而如文献[5]中定理3.1.2之证,可说明x(t)是方程(1)的具有初值ξ的解. H(T)E[ds. (8) 采用一个停时论证.令τn=T∧inf{t∈[0,T],‖xt‖≥n},只需以τn∧t代t证(8)式.但为记号简便,仍记τn∧t为t.此外约定f(t)=f(t,xt,r(t)),g(t)=g(t,xt,r(t)),hi(t)=hi(t,xt-,y,r(t))(i=1,2),则 K(T)E( 故得 1+K(T)≤1+ 然后用Gronwall不等式,即得所证. 引理1.2给出了方程(1)局部解的存在唯一性.类似文献[10]定理3.3存在性的证明与引理1.2唯一性的证明,可得如下全局解存在唯一性定理. 定理 2.1假设(A1)~(A4)成立且p>1.此外,假设存在一个函数V∈C1,2(τ×d×S)满足(i) ~(iii) . (i) 存在正常数c1、c2,使得 c1|x|p≤V(t,x,i) ≤c2|x|p, ∀(t,x,i)∈τ×d×S; (9) (ii) 存在常数l0∈(0,1),使得对任意的t∈0及有不等式 E|D(t,φ,i)|p≤lp0‖φ‖p0; (10) (11) 有 成立. 即方程(1)的零解p阶矩指数稳定. 证明对于任意有界初值ξ,要证(12)式成立,只需证明当0<γ<μ∧τ-1ln时,不等式成立: m(t)eγtE|x(t)|p≤β(1-κ1)-p, ∀t≥0, (13) 注意到,如果成立 (14) 则对t≥0时,利用条件(ii),有 M(t) κ1-p1E|D(s,xs,r(s))|p]≤ κ1-p1lp0eγs‖xs‖p0]≤ β(1-κ1)1-p+κ1M(t). (15) 于是M(t)≤β(1-κ1)-p<βq1e-γτ.因为m(t)≤M(t),因而只需要证明(14)式,即可得(13)式成立. 下面证明(14)式成立.为此需证 W(t)e ∀t≥0. (16) 由条件(ii)得 c2(1+l0)p-1[E|ξ(0)|p+ l01-pE|D(0,ξ,r(0))|p]≤ c2(1+l0)p‖ξ‖p0=βc1, 下用反证法.假设(16)式不对所有的t≥0成立,则必有最小的t1∈0,及充分小的δ>0,使得 W(t)≤βc1, ∀t∈[0,t1), W(t1)=βc1,W(t1+δ)>W(t1). 因为对任给的t∈[t1-τ,t1],当t≥0时,有 EV(t,x(t),r(t))≤c2E|x(t)|p= c2e-γtm(t)≤c2e-γtM(t) (17) 当t<0时,由γ与β的取值、W(t)的定义以及不等式(1-κ1)-p EV(t,x(t),r(t))≤ 从而有 E[V(t1,x(t1),r(t1))]< 因此,由r(t)的定义,对任意的t>0以及对充分小的δ′>0,有 EV(t,x ∀t∈[t1,t1+δ′). (19) 另一方面,对任意充分小的δ″>0,由V的定义以及It公式,有 r(s))g(s,x(s),r(s))]ds+ h1(s-,x(s-),y,r(s-)),r(s-))- h1(s-,x(s-),y,r(s-)),r(s-))- h2(s-,x(s-),y,r(s-)),r(s-))- (20) 令 M(δ″) h1(s-,x(s-),y,r(s-)),r(s-))- 显然M(δ″)是一个连续的局部鞅[11]. 对(20)式左右两边同时取期望,有 W(t1+δ″)-W(t1)= EV(t,xt,r(t))]dt≤0, 从而W(t1+δ″)≤W(t1),与t1的“最小性”相矛盾.因此,(16)式必对任何的的t≥0成立,于是(12)式成立.证毕. 在定理2.1的证明过程中,使用了如下事实: EV(t+θ,x(t+θ),r(t+θ))≤ 如果上述事实被 EV(t+θ,x(t+θ),r(t+θ))≤ 或者 EV(t+θ,x(t+θ),r(t+θ))≤ 所取代,则建立如下定理. 定理 2.2假设(A1)~(A4)成立且p>1.此外,假设存在一个函数V∈C1,2(τ×d×S)满足(i)~(iii). (i) 存在正常数c1,c2,使得 c1|x|p≤V(t,x,i) ≤c2|x|p, ∀(t,x,i)∈τ×d×S; (21) (ii) 存在常数l0∈(0,1),使得对任意的t∈0及有不等式 E|D(t,φ,i)|p≤lp0‖φ‖p0; (22) 对所有t≥0,有 定理 2.3假设(A1)~(A4)成立且p>1.此外,假设存在一个函数V∈C1,2(τ×d×S)满足(i)~(iii). (i) 存在正常数c1,c2,使得 c1|x|p≤V(t,x,i) ≤c2|x|p, ∀(t,x,i)∈τ×d×S; (23) (ii) 存在常数l0∈(0,1),使得对任意的t∈0及成立不等式: E|D(t,φ,i)|p≤lp0‖φ‖p0; (24) 对所有t≥0,有 考虑如下具Markov切换与Lévy噪声的中立型随机时滞微分方程 定理 3.1设p>1,且假设存在一个函数V∈C1,2(τ×d×S)满足(i)~(iv). (i) 存在正常数c1、c2,使得 c1|x|p≤V(t,x,i) ≤c2|x|p, ∀(t,x,i)∈τ×d×S; |D(t,x(t-δ0(t)),x(t-δ1(t)),…, x(t-δl(t)),r(t))|p≤ (26) φ(-δ1(t)),…,φ(-δl(t)),i)+ G(t,φ(0),φ(-δ1(t)),…,φ(-δl(t)),i)]+ φ(-δ1(t)),…,φ(-δl(t)),y,i),i)- φ(-δ1(t)),…,φ(-δl(t)), (27) 证明由(5)式函数V的定义可得: V(t,φ,i)= φ(-δl(t)),i)+ G(t,φ(0),φ(-δ1(t)),…,φ(-δl(t)),i)]+ H1(t,φ(0),φ(-δ1(t)),…,φ(-δl(t)),y,i) 成立,其中q是满足条件(iv)的常数,则由条件(iii)可得: E|D(t,x(t-δ0(t)),x(t-δ1(t)),…, x(t-δl(t)),r(t))|p≤ 因此,定理2.1的条件(ii)成立.这样,由定理2.1得方程(25)的零解p阶矩指数稳定.证毕. 特别地,考虑如下具Markov切换与Lévy噪声的中立型线性随机时滞微分方程 (A5) 存在常数εi(i=1,2,…,6),使得: 推论 3.2假设条件(A5)成立外,若存在正常数q,ai(i=1,2,…,n)以致ρ0<0,ρ1>0,ρ0+qρ1<0,并且 其中 其中I为d×d的单位矩阵.则方程(28)的零解均方指数稳定. 证明取Lyapunov函数为V(t,x,i)=ai|x|2,其中ai(i=1,2,…,n)为正常数,易验证定理3.1的条件成立,从而结论成立. 例 3.3考虑如下具Markov切换与Lévy噪声的中立型随机时滞微分方程 其中,x(t)=(x1(t),x2(t))T,w(t)是一个二维的布朗运动,{r(t),t≥0}是取值于有限状态S={1,2}的右连续Markov链,生成算子sint+0.3. 此外 并假设: 取Lyapunov函数为V(t,x,i)=ai|x|2,其中a1=0.6,a2=0.7.于是p=2,q的取值范围为:q>1.168 9. 不妨取q=2,经计算得ρ0=-4.249 4<0,ρ1=0.908 1>0且ρ0+qρ1=-2.433 2<0. 因此,由推论3.2得方程(29)的零解均方指数稳定.
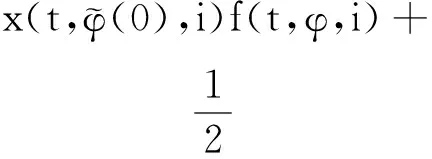
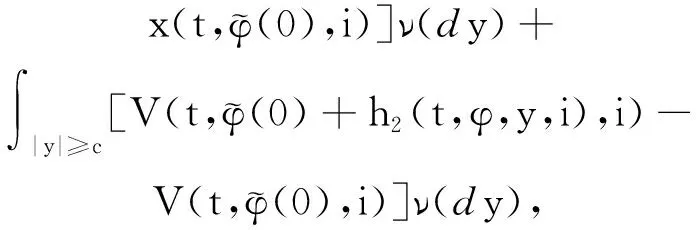
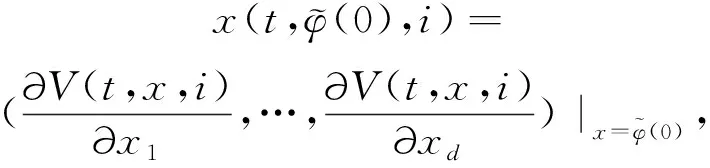
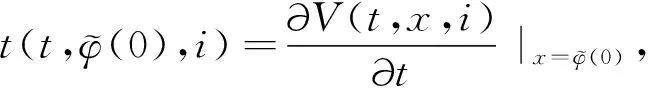
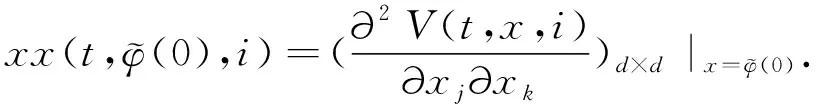
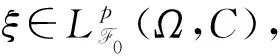


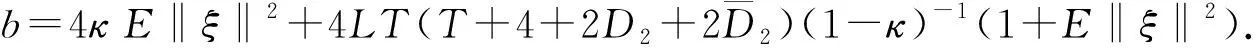

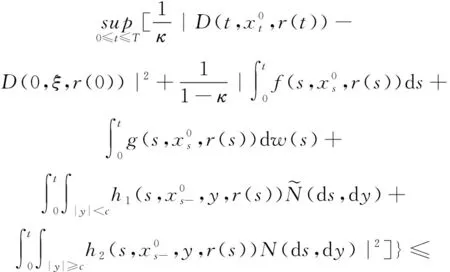
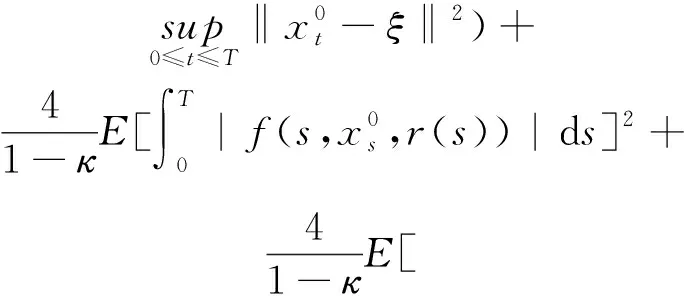
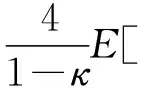
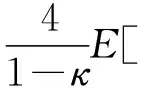

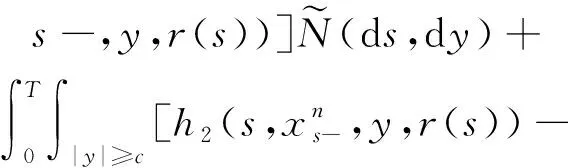
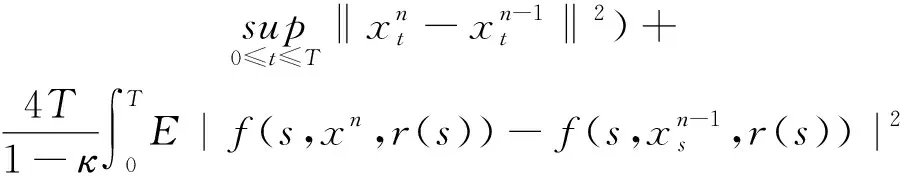
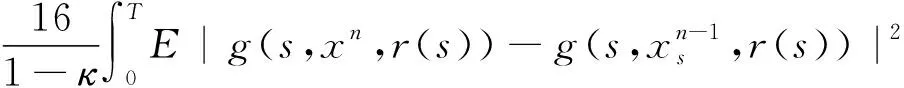
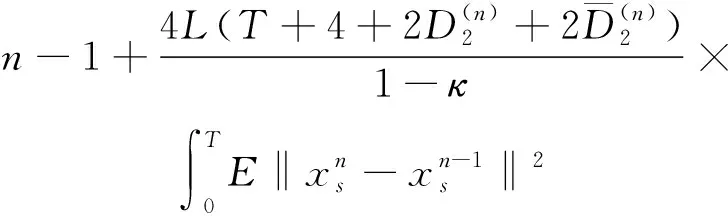
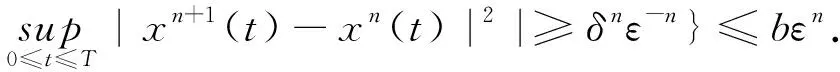
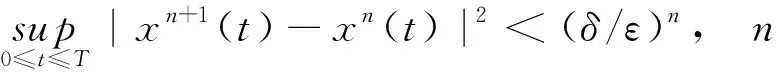


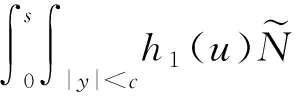
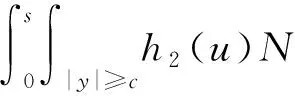
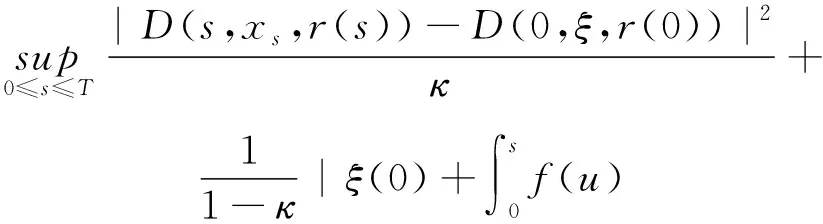
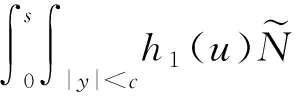
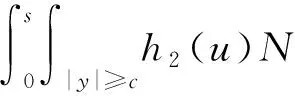

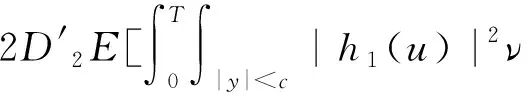
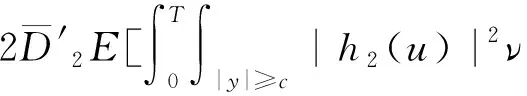
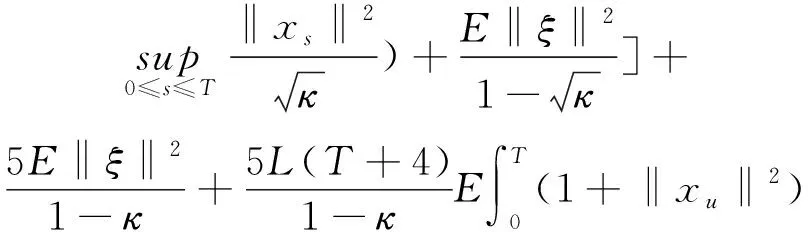
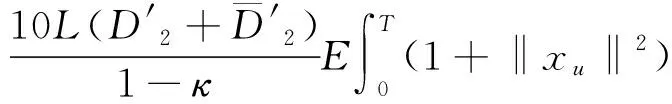
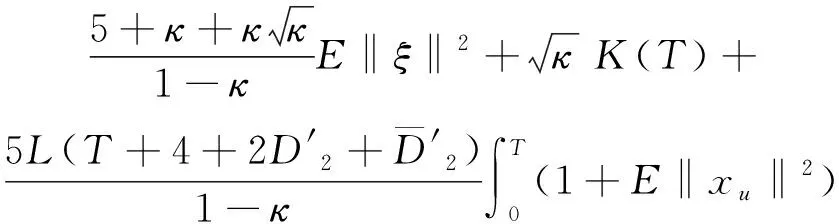


2 主要结果



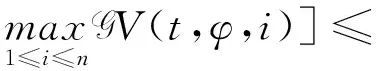
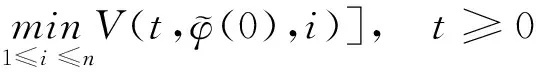

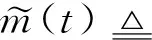
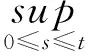
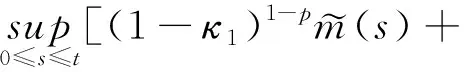
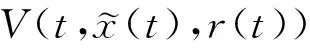

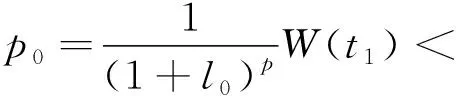


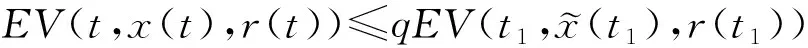
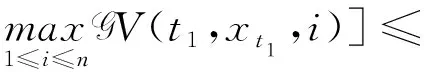

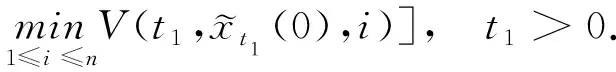
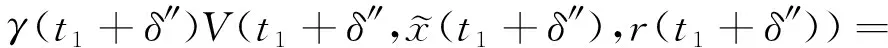
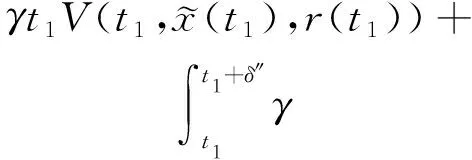
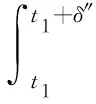
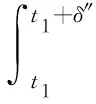
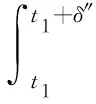
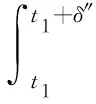
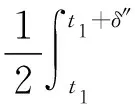
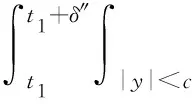
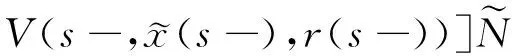
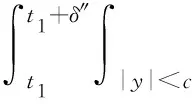
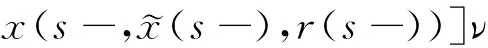
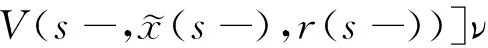
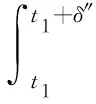
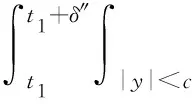
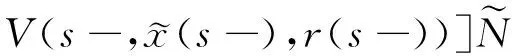
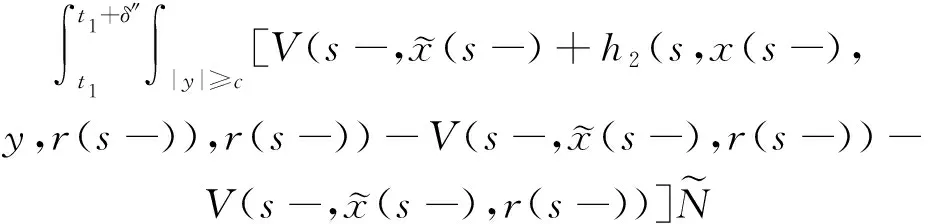
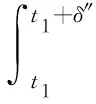

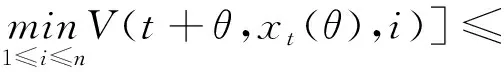



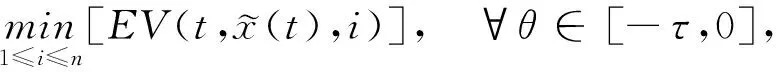

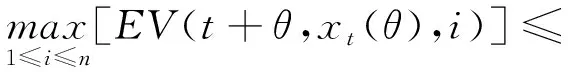
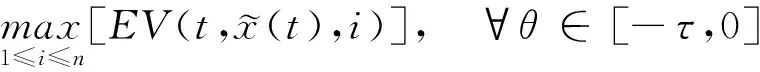


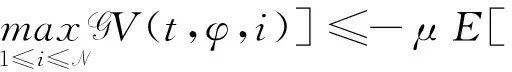

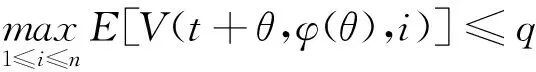
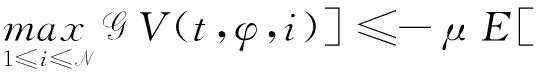
3 应用