一类偏微分方程在半无穷区域上的空间渐近性质
李远飞, 肖胜中, 石金诚
(1. 广州华商学院 数据科学学院, 广东 广州 511300; 2. 广东农工商职业技术学院 科研处, 广东 广州 510507)
从数学的角度来研究各种模型时,首先要关心的是这些模型解的全局存在性以及不存在性.在文献中最常见的是研究模型的解关于时间变量的存在性,文献[1-2]分别研究了变系数的热量方程以及高维空间上抛物方程在非线性边界条件下解的爆破现象,在对已知数据项进行一定假设的情形下,通过巧妙的设置辅助函数,得到了爆破时间的上下界以及全局解存在的条件.文献[3]考虑了更一般的非线性抛物方程的情形.
本文关注一类来自黏弹性问题的偏微分方程在一个半无穷柱体上的空间存在性和衰减性,这种研究通常被称为Phragmén-Lindelöf型二择一研究.与空间衰减性不同,这种研究不需要假设方程的解柱体的无限端方程的解趋近于零这种先验假设,而是证明方程的解随距柱体有限端的距离要么指数式增长要么指数式衰减.由于Phragmén-Lindelöf型原理在力学、生物学等学科上的广泛应用,自20世纪90年代以来逐步取代Saint-Venant原理而成为研究的热点,出现了大量的成果[4-14].
本文假设Ω表示一个半无穷柱体的内部区域,柱体的有限端记为D位于x1Ox2平面上,柱体的母线平行于x3坐标轴,即
Ω={(x1,x2,x3)|(x1,x2)∈D,x3>0}.
令D(z)表示Ω在x3=z处的截面,即
D(z)={(x1,x2,x3)|(x1,x2)∈D,
x3=z>0}.
本文采取通常所用的符号约定,即用逗号表示求导,重复希腊字母表示从1至2求和,重复英文字母表示从1至3求和,例如:
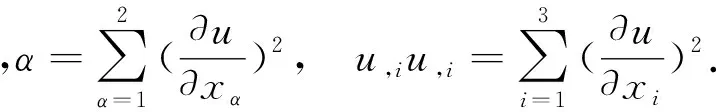
1 准备工作
本文研究以下来自黏弹性问题的偏微分方程[8]:
c(x)utt=[ρ(x,|u|2)u,i],i+γΔut,
inΩ×(0,t),
(1)
u=0, in ∂D×{x3>0}×(0,t),
(2)
u=f(x1,x2,t), inD×{x3=0}×(0,t), (3)
u(x,0)=0, inΩ,
(4)
其中∂D表示区域D的边界,△表示三维拉普拉斯算子,表示梯度算子,f是给定的已知函数,x=(x1,x2,x3)以及γ是一个大于零的常数.这类方程也存在于第三类热传导的研究中.第三类热传导的线性形式满足我们的假设.注意到,在二维情况下,如果ρ满足一定的条件时,则方程(1)对应于幂律材料子类的反平面剪切动力学变形[15].
注意到文献[16]研究了定义在Ω上的二阶拟线性方程
[ρ(x,|u|2)u,i],i=f(u),
在柱体的侧面上施加了齐次Dirichlet条件和Neumman边界条件.他们证明了当空间变量趋近于无穷时方程解的空间二择性.当f(u)=0时,文献[17-18]分别考虑了非稳态和稳态的情形下在二维区域上解的空间衰减性.本文的主要目的把文献中取得的结果进一步推广到模型(1)中来.为此,本文利用加权的能量分析法,在“能量”函数中引入一个待定的大于零的参数,由于此参数是任意的正数,可以得到比上述文献更快的衰减率.
假设c(x)和ρ分别满足以下条件:
(a) 0 (5) 现在定义能量函数 (6) 由(5)式可得 (7) 设z0为x3坐标轴上的某一个点.在(6)式中利用散度定理、方程(1)~(4)和(7)式可得 (8) 对(8)式微分可得 (9) (10) χ(z,t)+(0,t). 下一节利用Hölder不等式来推导本文的主要结果,在此过程中没有使用Schwarz不等式.虽然考虑的是三维的情形,但是事实上本文的分析与空间的维数无关.因此,本文的结果对一维和二维的情形也是成立的. 利用Hölder不等式和算术几何平均不等式以及条件(a)和(b),可得 |I1|≤ (11) (12) 接下来做以下2种情形分析. (H1) 如果存在z0使得(z0,t)≥0,由于(z,t)≥0,所以(z,t)≥(z0,t)≥0,z≥z0.此时结合(6)式、(11)式和(12)式,可得 (13) 由(13)式可得 z≥z0. (14) 对(14)式从z0到z积分,可得 (z,t)≥(z0,t)edAdτ+ 现定义 (16) 联合(15)式和条件(a),可得 (17) 其中 对(17)式从z0到z积分,可得 (18) (19) (H2) 如果对任意的z≥0都有(z,t)<0,则结合(6)式、(11)式和(12)式,可得 (20) 由(20)式可得 z≥0. (21) 对(21)式从0到z积分,可得 (z,t)≥(0,t)edAdτ- 由于 所以由(22)式可知当z→∞时-(z,t)指数式衰减于零.联合(10)式,可得 O(1), (23) 其中O(1)表示当z→∞时的无穷小.把上述分析总结为以下定理. 定理 1设u是方程(1)~(4)的解,其中c(x)和ρ分别满足条件(a)和(b),则当z→∞时函数(z,t)要么指数式增长要么指数式衰减,即要么(19)式成立要么(23)式成立. 注 1注意到在定理1中获得的衰减率和增长率与ω相关,而ω是一个任意的常数,所以本文获得的衰减率和增长率要比文献中取得指数式衰减率和增长率更快. 注 2由(23)式可知,要使得衰减界有意义,还必须推导-(0,t)的显式上界. (24) 以及 (25) 记 S(x1,x2,x3,t)=f(x1,x2,t)e-βx3,β>0. 于是由(24)式和方程(1)~(4),可得 B1+B2+B3+B4+B5. (26) 利用Schwarz不等式和算术几何平均不等式,可得: (27) (28) (29) (31) 取 再把(27)~(31)式代入到(26)式,结合(25)式可得 即 -(0,t)≤C(t), 其中 假设c(x)仍然满足条件(a),但是条件(b)由以下条件代替 其中K1和K2为大于零的常数.文献[5,14-15]研究过和(b*)类似的条件.满足条件(b*)的例子可以写为 取K1=K2=1,易证上述函数满足条件(b*). 于是利用条件(b*)计算可得 (32) 把(32)式代入到(11)式可得 |I1|≤ (33) 仍然考虑以下2种情形. (H1) 如果存在z0使得(z0,t)≥0,由于F(z,t)<0,所以(z,t)≥(z0,t)≥0,z≥z0.此时结合(6)式、(12)式和(33)式,可得 (34) 通过与(13)式类似的计算,由(34)式可得 (35) 其中C1是一个大于零的常数. (H2) 如果对任意的z≥0都有(z,t)≤0,则结合(6)式、(12)式和(33)式,可得 -(z,t)=-I1-I2≤ (36) 通过与(20)式类似的计算,由(36)式可得 (37) 其中C2与-(0,t)和dAdτ相关. 把上述分析总结为以下定理. 定理 2设u是方程(1)~(4)的解,其中c(x)和ρ分别满足条件(a)和条件(b*),则当z→∞时函数(z,t)要么指数式增长要么指数式衰减,即要么(35)式成立要么(37)式成立. 本文研究了方程组(1)~(4)解的空间性质,得到了解的空间增长率和衰减率.解的指数式增长也被称为解的空间不存在性或空间blow-up.通过设置任意参数ω,证明了增长率和衰减率要比文献中的结果更快.此外,本文的结果对一维和二维区域上的情形同样成立.同时,本文仍有更深层次的问题需要研究.一是如果柱体区域被一个锥形区域代替,例如文献[9-19]分别研究了三维调和方程和二维复调和方程在锥形区域上的空间二择性;二是在实际状况中,一个物理现象不可能在柱体的侧面上总是满足齐次Dirichlet条件或Neumann条件.因为由于自然风化、腐蚀或其他原因都会对柱体的侧面造成一定的损伤,在这种情况下就需要考虑非齐次边界条件或者局部非齐次边界条件,文献出现了一些相关结果[4,7,11].显然,这些文献研究的模型大多比较简单,把这些结果推广到方程(1)~(4)甚至更复杂的模型中来是非常有意义的. 致谢广州华商学院科研团队项目(2021HSKT01)对本文给予了资助,谨致谢意.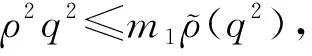
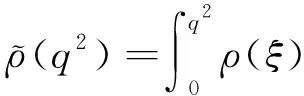
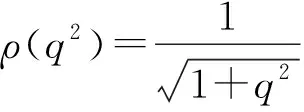
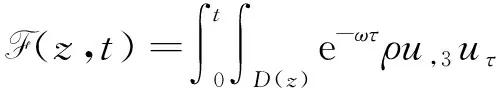
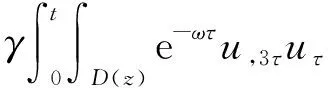
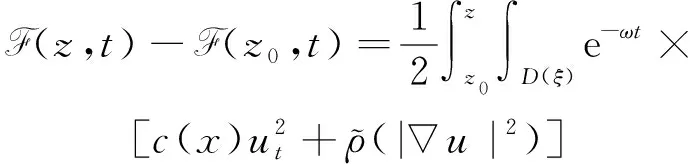
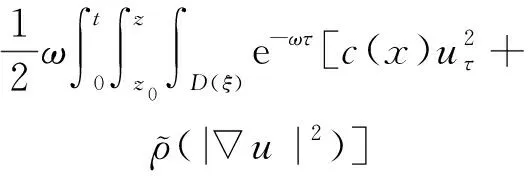
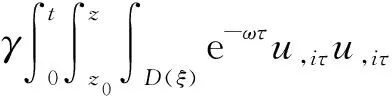
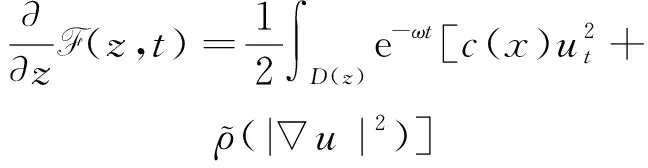

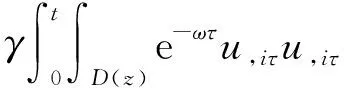
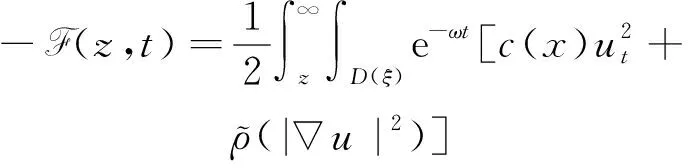
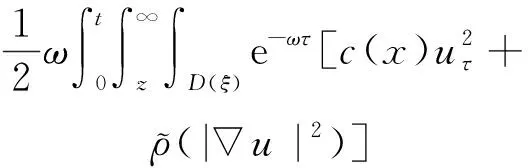
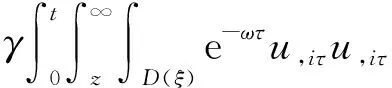
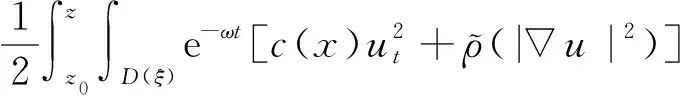
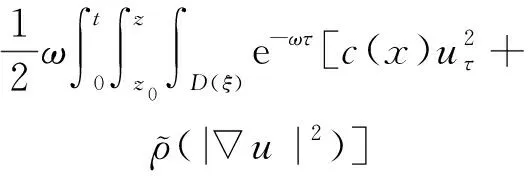
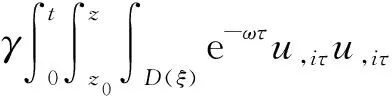
2 空间渐近性质
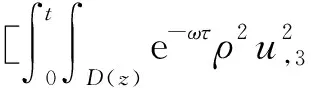
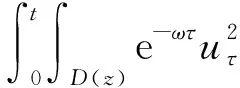
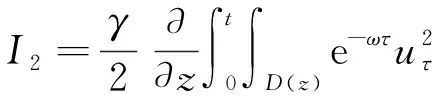
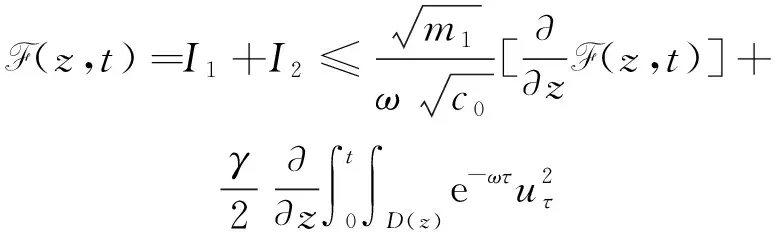
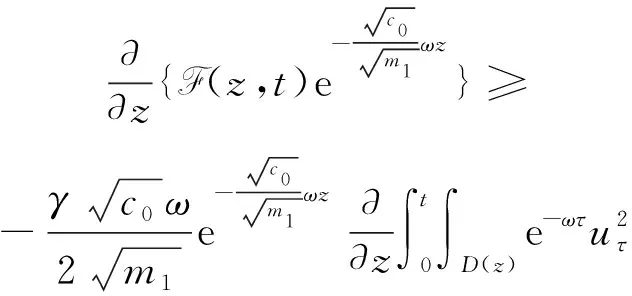
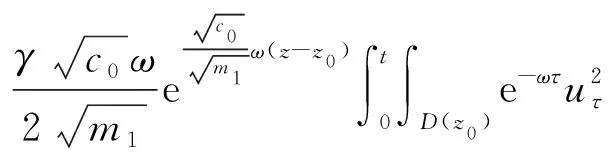

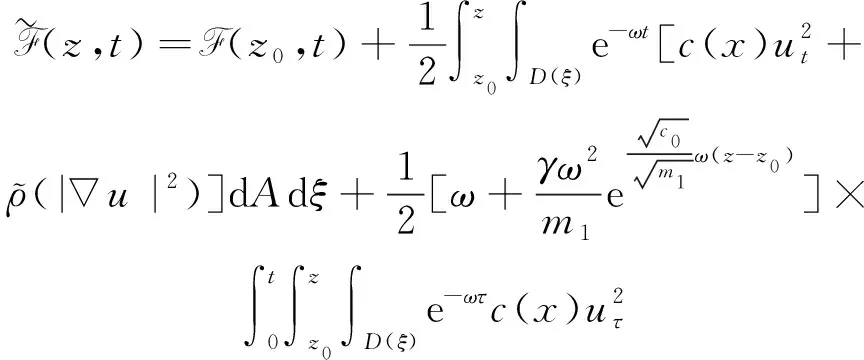
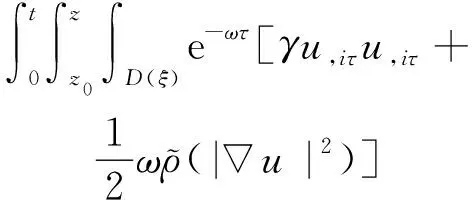

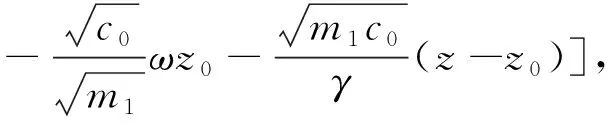
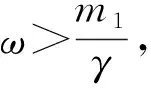
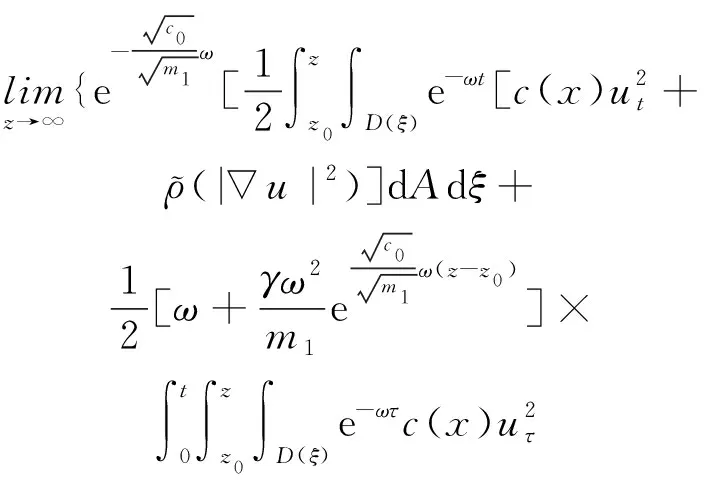
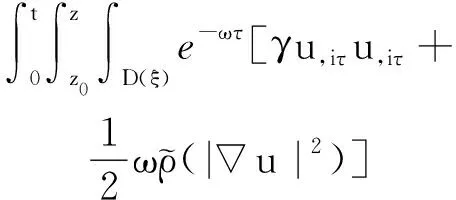
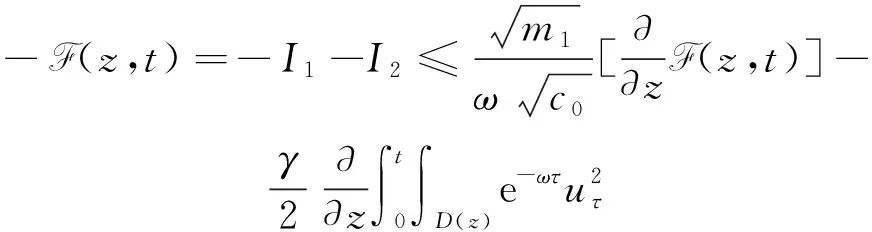
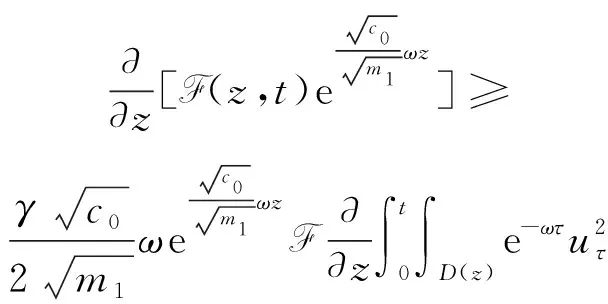
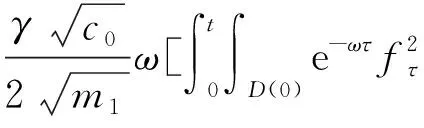

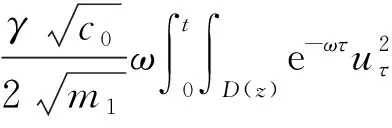
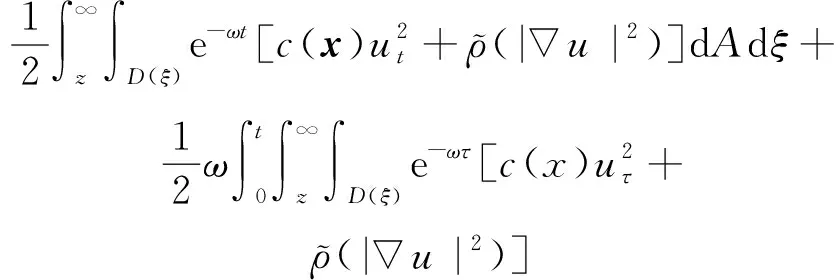
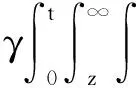
3 全能量估计
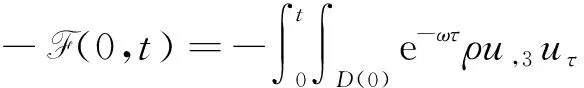
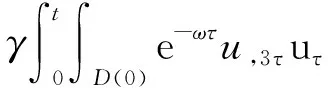
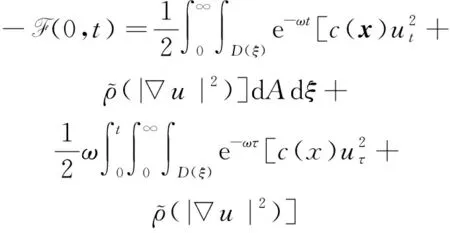
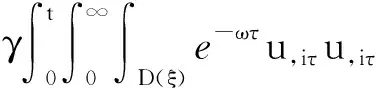
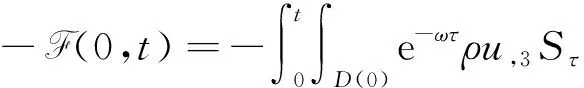
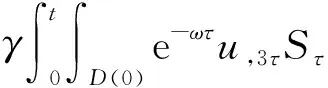
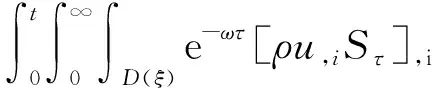
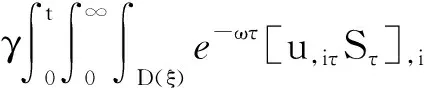
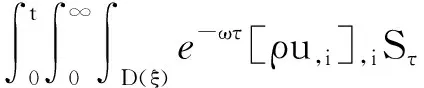
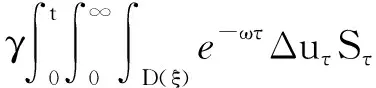
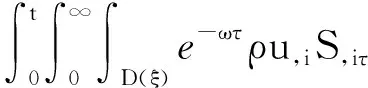
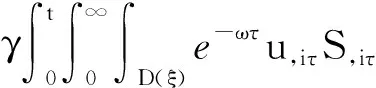
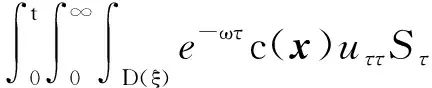
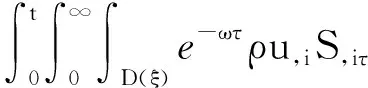
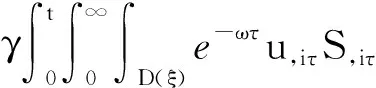
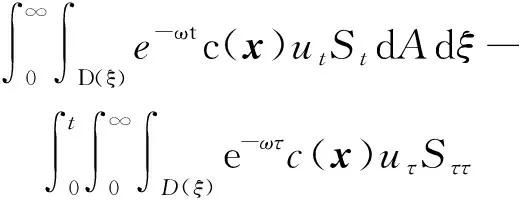
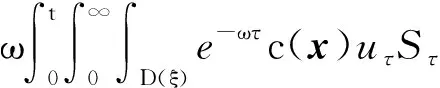
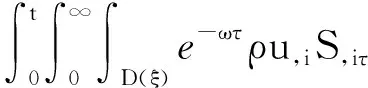
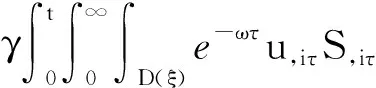
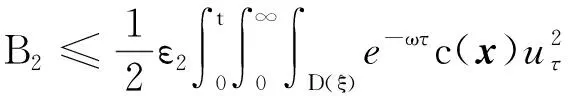
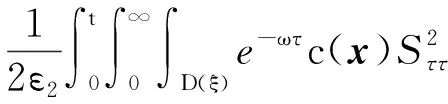
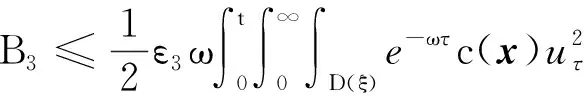
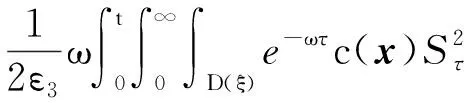
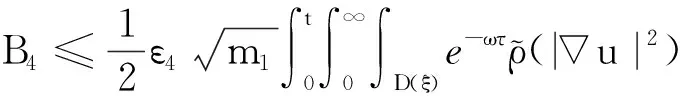
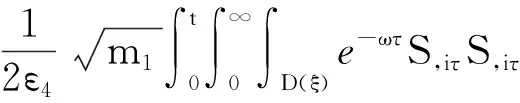
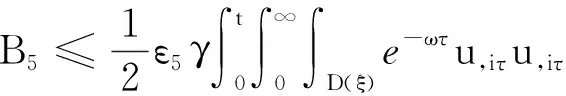
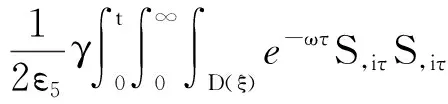
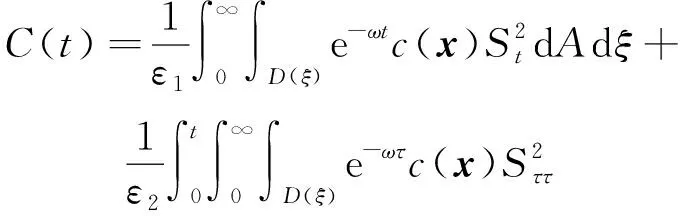
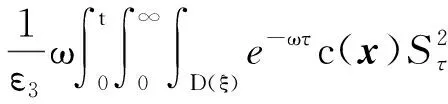
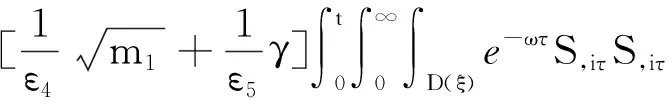
4 新条件下解的空间性质
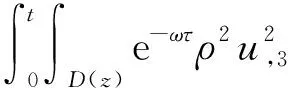
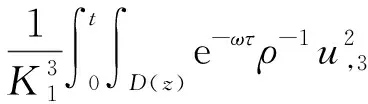
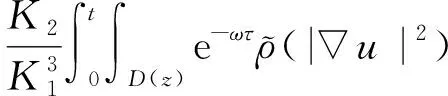
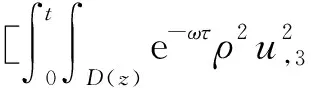
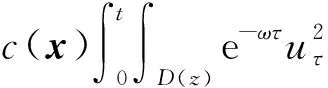


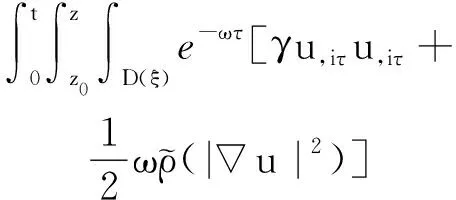
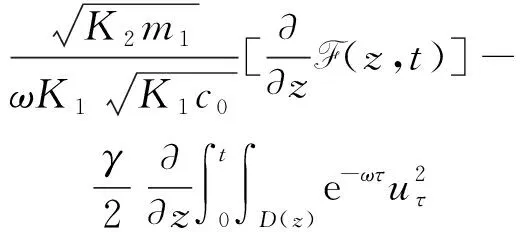
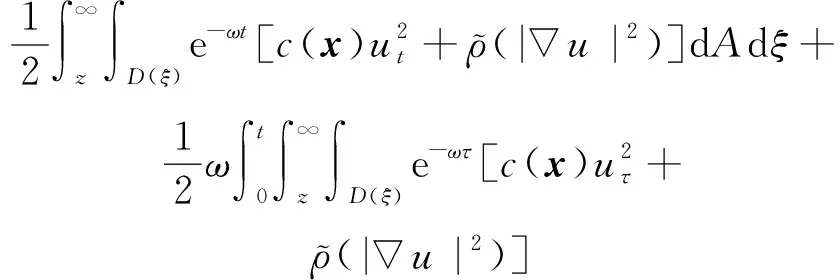
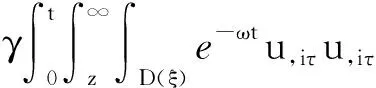
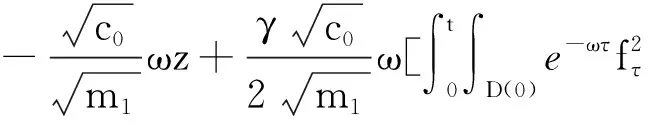
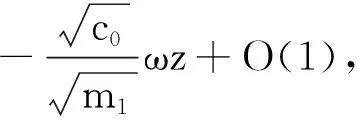
5 结论

