泛函积分方法与金属氢星体模型中物态性质与温度及磁场涨落研究
赵 丰, 颜 骏, 周良建, 詹 路, 黄 忆
(四川师范大学 物理与电子工程学院, 四川 成都 610066)
泛函积分方法来源于量子场论和粒子物理的研究,目前在物理学的各个领域都有广泛的应用.泛函积分是一种非常灵活的数学工具,也是现代理论物理中最强有力的方法之一[1-4],这类方法特别适用于计算统计物理中的集体激发谱,如库仑相互作用粒子系统中的等离子体振荡,有限温度下的玻色凝聚,超流和超导理论中的量子涡旋和长波声子,极化子的自能等问题.泛函积分方法还可以使相变、激光、Kondo效应、伊辛模型等理论中的复杂问题变得相对简单.俄罗斯学者Popov[1-2]和德国学者Kleinert[4]曾对泛函积分方法进行过比较系统的研究并做出了重要贡献.
近年来,四川师范大学课题组将泛函积分方法应用于物理学的各个领域,取得了一系列的研究成果.在统计物理和凝聚态物理方面,有原子光学中的Dicke模型[5],高温超导中的Boson-Fermion模型[6-7],费米凝聚中的sine-Gordon-Thirring模型[8-12],反铁磁体中的三带Hubbard模型[13-14],主要研究了上述模型中的激发谱、自由能、费米子凝聚谱等物理性质,还计算了随机散射通道模型中传递函数的概率分布函数[15].在引力物理和相对论天体物理方面,根据泛函积分方法研究了非对易时空中费米物质的集体激发谱[16],导出了点物质黑洞背景下物质的量子涨落和关联函数[17-19],计算了暗能量混合的费米孤子星的质量和物态参量[20].在研究这些物理问题的过程中,形成了一种新的变分泛函积分方法,这一方法可以有效地研究模型在强耦合区间的的物理性质.
金属氢是超高压环境中形成的一种特殊物质,通常存在固态金属氢和液态金属氢2种物态.固态金属氢中离子能保持晶格结构,具有一定导电性质,在更强的压力下固态金属氢中晶格结构被破坏并转化为液态形式的金属氢,所以在高压环境下的金属氢密度比普通氢的密度更大.在地球上不存在自然的金属氢,人们只有在实验室通过人工合成固态金属氢,这是目前高压凝聚态物理中具有挑战性的研究课题.
木星是太阳系中存在的一种重型的巨行星,在巨大压力下其内部可能形成液态形式的金属氢,在木星较快的自转作用下金属氢中的电子将形成较强的电流,从而对木星的磁场的形成和强度产生重要的影响.瑞士天体物理学家Mayor和Queloz[21]由于发现了系外巨行星获得了2019年度诺贝尔物理奖,这些巨行星中也可能存在不同形式的金属氢物质[22],因此,研究金属氢对理解巨行星的各种天文学观测性质就具有重要的物理意义.
本文将根据泛函积分方法研究金属氢的物态关系,并进一步分析转动巨行星中的流体力学性质,磁场强度涨落和温度涨落等物理效应.
1 泛函积分与致密电子-离子系统的晶体结构
本节将在泛函积分方法框架下探讨晶体结构的微观理论,该方法由Popov[1]于1981年提出,之后加以推广[2].晶体理论的泛函积分方法还可用来研究稠密电子-离子系统的周期晶格,这一方法由Anisimov等[23]于1986年提出.一个具有库伦相互作用的电子和离子组成的系统中,晶体的性质是由集体激发声子决定的,一个微观理论必须描述声子-电子和离子系统的相互作用,泛函积分方法可以完成这项工作.主要操作思想是将电子和离子的原始作用量转为用电势场φ(x,τ)描述的有效泛函作用量,再从有效泛函作用量的稳定条件找到定态场φ0(x),并考虑Seff稳定点附近的涨落效应.
金属氢模型中电子和离子系统的泛函作用量为
其中
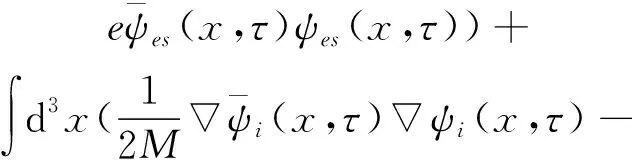
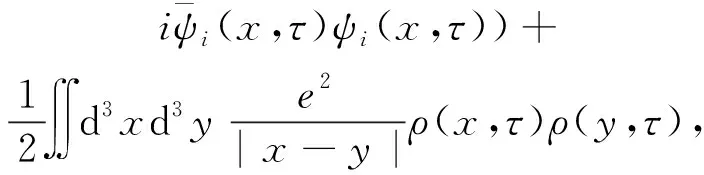
(2)
(3)
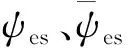
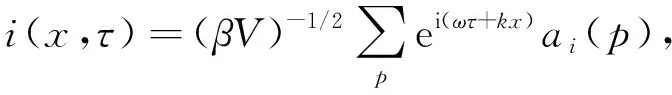
(4)
其中,p=(k,ω)是动量,松原频率为ω=(2n+1)π/β,β-1=T是有限温度,λi是化学势.首先将库仑相互作用转换为电势玻色场φ(x,τ)的作用,引入如下高斯积分:
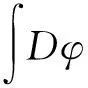
(5)
再对φ(x,τ)进行移位变换
(6)
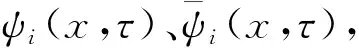

(7)
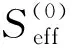
Seff[pl,α,ql,α,φ(x,τ)]=
2lndet[∂τ+(2m)-12+λe+ieφ(x,τ)]/∂τ+
(2m)-12+λe+
ieφ(ql,α(τ),τ)],
(8)
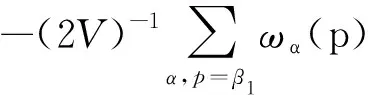
(9)
其中p0和ρ5/3成正比,(7)式中第3项可以展开为
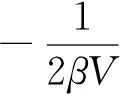
(10)
其中Π是格林函数的极化算子,所以有
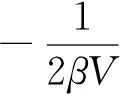
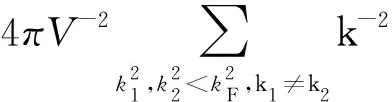
(11)
(12)
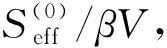
exp(-ηπn2+2πi(n,γ-δ))+
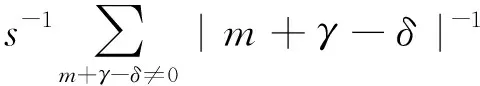
|m+γ-δ|)-ηs-2η-1/2},
(13)
其中
(14)
C1=2.837 297 479 482,
体心立方晶格(bcc)中
C2=2.888 461 503 050,
面心立方晶格(fcc)中
C3=2.888 282 119 020,
六角密堆晶格(hcp)中
C4=2.888 168 750 480,
(7)式最后1项修正项表示零点能,在大压强下满足
2 金属氢中的晶体-液体转化
利用金属理论的泛函积分方法可证明,随着压强进一步增加,晶体系统可能变为液态,这时晶格的零点振动将被破坏.为了计算固态金属氢转化为液态金属的临界密度,应先计算液态金属氢的压强,然后再与第1节已计算的固态金属氢的压强进行比较,这一压强前3项的表达式[23]为
(15)
参数M-1/2的存在确保了零点振动能带来的影响,液态金属氢的压强[24]为
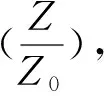
(16)
其中
(17)
是理想费米电子气体和等离子气体的混合压强,Z是具有库仑作用的电中性等离子体的配分函数.为了计算(βV)-1ln(Z/Z0),可采用如下等离子体作用量
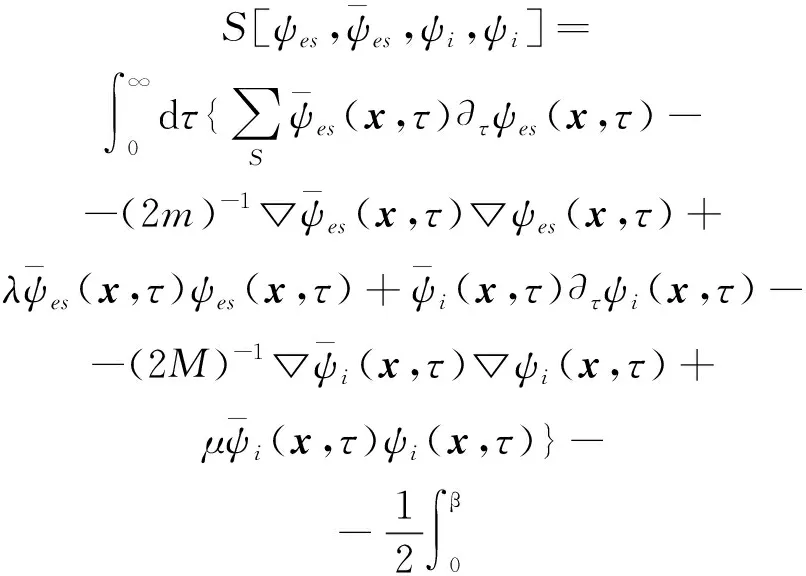
其中电荷密度ρ(x,τ)为
ρ(x,τ)=ρi(x,τ)-ρe(x,τ)=
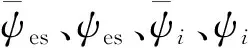
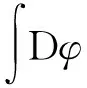
再进行下列移位变换后消去非局域库仑项
最后得到如下作用量
ieφ(x,τ))ψes(x,τ)+
ieφ(x,τ))ψi(x,τ)}.
(22)
对电子、离子费米场进行泛函积分后得到的有效作用量为
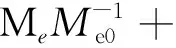
(23)
并引入记号
Me=∂τ+(2m)-12+λ+ieφ(x,τ),
Me0=Me|φ=0;
Mi=∂τ+(2m)-12+μ-ieφ(x,τ),
Mi0=Mi|φ=0.
(24)
考虑了电子自旋后lndet前会出现2,将(23)式中φ的幂展开到2阶后得自由电子的格林函数Ges,以及离子的格林函数Gi,对φ场积分后得如下压强的修正表达式
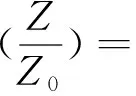
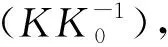
(25)
其中矩阵元K与电子和的离子的格林函数极化算符有关,这里极化算符表示电子和离子的自由电子的格林函数乘积之和.再将lndet展开并取低温极限后压强的修正表达式为
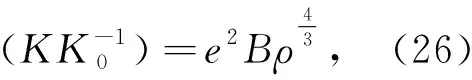
根据(17)和(26)式得如下液体金属氢的物态关系
(27)
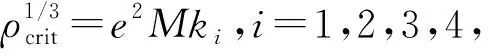
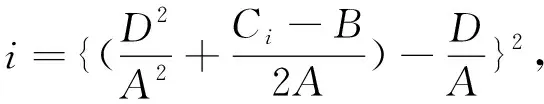
(28)
与不同类型晶格中常数Ci有关系,其余常数的数值分为
A=1.914 156 000,B=1.477 117 533,
D=1.534 990 062,
所以不同类型晶格的金属氢转化为液态金属氢时的临界粒子数密度有一定的差异.
3 转动星体中的流体力学性质
转动情况下的星体平衡方程[25-26]为
(29)
(30)
其中,
此时径向微分方程(29)的解为
(31)
其中
N=(4πGβ2d2-2ω2d),
M=4πGβ2d2·(5/3ρc)>0.
所以积分常数应取C1=C2=0,根据(31)式可进一步导出粒子数密度的涨落比值为
(32)
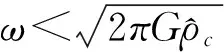
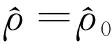
(33)
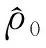
(34)
将(33)式代入方程(34)可导出如下修正形式的Lane-Emden方程
(35)
其中,ξ=Dr,U=Φ/k1,f=(ω/D)2×(1/3k1).文献[29]采用变参数法讨论了Lane-Emden方程的近似解,文献[30-31]分析了木星中多方指数n=1,2时Lane-Emden方程密度的解析解,下面进一步研究2阶非线性微分方程(35)的级数解.这时边界条件设为:当ξ=0时,U=0,dU/dξ=0,确定星体半径的条件为:当ξ=ξn时,U=0.将方程的解用级数展开为
U=a0+a1ξ+a2ξ2+
a3ξ3+a4ξ4+a5ξ5+a6ξ6,
(36)
根据边界条件可以定出其中的系数分别为
(37)
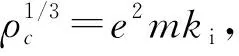
扰动时行星表面附近的流体元的运动方程[32]为
(38)
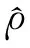
(39)
由此可以得到声波在星体内部的传播时间约为
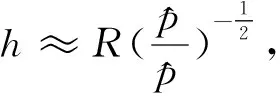
(40)
声波的传播速度约为
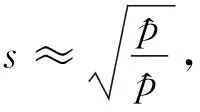
(41)
液态金属氢的物态方程为
(42)
其中,
k1=α1/α,α=C/M,k2=α2/α4/5,
α1=(1/me+1/M)A,α2=e2B,
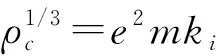
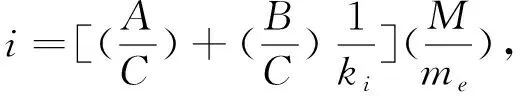
(43)
其中数值常数
A=1.914 156 000,B=1.477 117 533,
C=2.871 230 000.
根据(40)和(43)式可以计算出4种类型金属氢星体中声波传播时间的比值约为
τ1∶τ2∶τ3∶τ4=
1.218 61∶1.218 60∶1.218 60∶1.218 60.(44)
所以不同类型的金属氢星体的声波传播时间几乎一致,如木星中sc晶格的声波传播时间约为1 958.355 0 s,bcc晶格,fcc晶格和hcp晶格的声波传播时间约为1 958.338 5 s,其中SC晶格和其余3种晶格的传播时间只有微小差别.
4 星体中磁场和温度的涨落关系
设星体内矢势A满足的方程为
2A=-μ0J,A=0,
(45)
其中J是流密度,那么方程的解为
(46)
其中x′是源点,x是场点,r为x′到x的距离,对解求旋度即可导出磁场感应强度的表达式,即
B=×A=
(48)
在具体计算中可设星体半径为R,总电荷量为Q,则Q=(4πR3/3)ne,这里ne表示电荷的粒子数密度.在球坐标下J(x′)=neω×r′,ω是星体的转动角速度.当r (49) (50) δB1∶δB2∶δB3∶δB4≈ 51 105.53∶50 955.75∶50 926.57∶50 908.22,(51) 这时,磁场强度的比值逐渐变小,文献[31]给出的木星内部的磁场强度和角速度及密度之间的关系式为B~(ρω)1/2,这与本文讨论的类似关系在定性上是一致的. 如果转动的木星处在太阳恒星的辐射场之中,那么边界条件要求在木星的表面上输入远处太阳的能流密度,这时传播到木星表面上的辐射波为平面波,表面上的能流密度为I=I0sinθcos(ωt-φ),这里ω是木星的自转角速度,I0是常数. 星体内部温度场T(r)满足的扩散微分方程为[33] (52) 将这一方程的解设为T(r)=R(r)Y(θ,φ)e-iωt,其中D=k/ρc是热扩散率,其中k是热导率,ρ是物质密度,c是物质的比热.分离变量后的径向微分方程变为 当l=1时,方程(53)的径向解为 (54) 其中,j1是第1类1阶球贝塞尔函数,所以木星内部温度分布的解可表示为 (55) 其中系数A可以由边界条件确定,即 (56) 因此星体内部的温度分布的完整解为 T(r,θ,φ,t)= (57) (58) δT1∶δT2∶δT3∶δT4≈ 1.481∶1.491∶1.493∶1.494, (59) 这时温度的涨落比值由小逐渐变大,如果木星内部温度取为T=2 000 K,sc晶格对应的温度涨落为δT1/T=5%,那么δT1=100 K,此时hcp晶格对应的温度涨落为δT2=100.88 K,所以不同类型晶格对应的温度涨落相差都较小. 本文根据泛函积分方法研究了金属氢的物态性质,在此基础上进一步研究了木星的流体力学性质,以及磁场和温度的涨落关系. 本文首先简述了泛函积分方法在物理学各个领域中的应用,介绍了金属氢和木星内部的物理性质.其次,本文采用泛函积分方法推导了致密电子-离子系统的压强和有效作用量,给出了各种晶格作用量的数值计算结果,另外,还导出了液态金属氢的有效作用量和压强表达式.随着压强的增大,固态金属氢将转化为液态金属氢,其临界粒子数密度不仅和离子质量M有关,而且很依赖于不同类型的晶格常数Ci,在固体物理中通常的晶格有:sc简单立方晶格、bcc体心立方晶格、fcc面心立方晶格以及hcp六角密堆晶格. 另外,本文还将金属氢的物态关系应用于木星的表观物理性质研究,重点研究了木星的流体力学性质,电磁学和热力学性质.根据转动星体的平衡方程的解分析了均匀密度下的粒子数密度涨落,结果发现当涨落δ<0时,星体处于平衡状态,δ>0时,星体呈现不稳定状态.本文还根据金属氢的物态方程推导了修正的Lane-Emden方程,给出了方程的6阶级数解,计算了木星的角速度和其密度的比值,结果表明木星的自转角速度ω对L-E方程的解影响很小,所以计算木星的质量和密度时可忽略角速度这一因素. 本文还采用流体元的运动方程和液态金属氢的物态关系,估算了声波的传播时间的比值,这一比值与不同类型晶格的有效物态参量有关,但其数值仅有很小的差别.另外,在均匀密度星体中磁场强度的涨落和其温度和晶格常数呈一定的比例关系,4种不同类型晶格对应的磁场强度的涨落比值也比较接近. 本文根据扩散方程的解分析了星体内部的温度分布,给出了温度涨落的表达式,结果发现温度涨落也与晶格常数呈一定的比例关系,在温度涨落中是负指数,在磁场涨落中是正指数,所以温度涨落逐渐变大,磁场涨落逐渐变小. 本文主要研究一种理想状态下的均匀金属氢星体模型,分析和讨论了星体内部的力学、电磁学和热力学等表观物理性质,本文的研究结果具有一定的定性意义,对进一步研究木星等巨行星内部的物理性质提供一种研究思路和方法上的启示.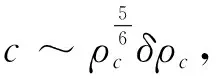
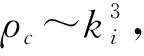
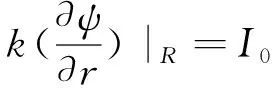
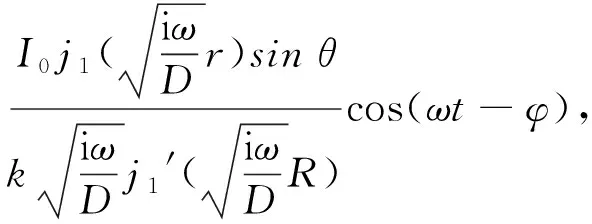
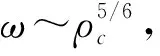
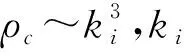
5 结论与讨论

