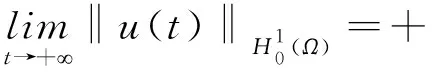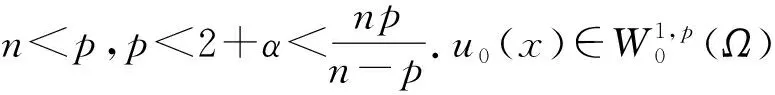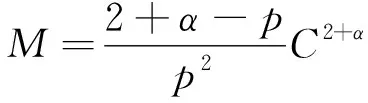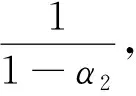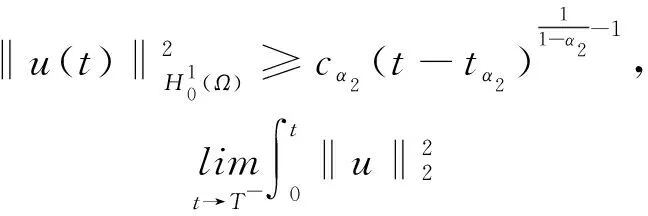一类半线性伪抛物方程的初边值问题
高雪妍, 郑雅匀, 杨 晗
(西南交通大学 数学学院, 四川 成都 611756)
0 引言
研究半线性伪抛物方程的初边值问题
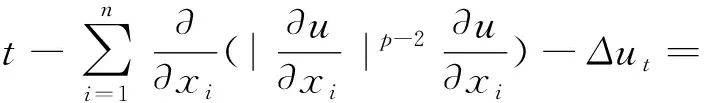
φ(u),Ω×(0,T),
(1)
u(x,t)=0, ∂Ω×(0,T),
(2)
u(x,t)=u0(x),Ω,
(3)
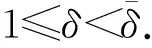
其中
这里Ω⊂n是一个边界充分光滑的有界区域,p≥2.上述方程组可用来描述非线性、色散、长波的单向传播[1-2]和种群的聚集[3]等多种现象,也可用于分析有缘半导体中的非平稳过程[4-5].Δut-ut对应自由电子密度率,ut对应自由电荷电流的线性耗散,φ(u)描述自由电子电流的来源.
现回顾与问题(1)~(3)有关的文献的一些经典结论.当(1)式中Δut项缺失时,Tsutsumi[6]研究了退化抛物型方程

的初边值问题.用Galerkin方法、单调算子理论和紧致性定理研究了方程的整体弱解的存在性与爆破方面的结论.当(1)式Δut项变成u时,Liu等[7]考虑了半线性热方程
ut-Δu+u=|u|p-1u
(4)
的柯西问题.在初值属于稳定性集时,研究了方程(4)弱解的整体存在性和指数衰减估计,在初值属于不稳定性集时,研究了弱解在有限时刻爆破.Xu等[8]等研究了半线性伪抛物方程
ut-Δu-Δut=u1+α
(5)
的初边值问题.在初始值满足适当的条件下,通过引入稳定性集与不稳定性集得到弱解的整体存在性、渐近性和不存在性,并通过比较原理得到具有初始能量为正时解在有限时刻爆破.Chen等[9]研究了具有对数非线性项的半线性伪抛物方程
ut-Δu-Δut=ulog|u|,
通过使用对数Sobolev不等式和一族势井,得到方程整体弱解存在性、解的渐近性质和在正无穷处的指数增长性.另一方面,还讨论了解的真空隔离.
本文研究(5)式的退化情形,即(1)式,考虑初值在何种条件下弱解的整体存在及在何种条件下解爆破,并且研究解存在真空隔离现象.
1 准备工作
为了后面的应用,先给出几个引理,引理1.1和1.2的证明详见文献[6].
令
I(u)=a(u)-b(u),
(6)
其中
下面是与势井理论相关的基本结论.
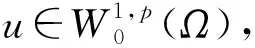
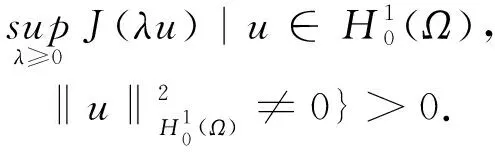
(7)
引入集合
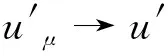
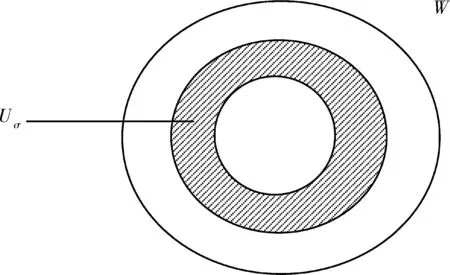
W={u|u∈W1,p0(Ω),0≤J(λu) λ∈[0,1]}. 事实上,可证得对任意t,u0(x)∈W时,u(x)∈W(见定理3.1).因此,称该集合为稳定性集. 引理 1.2 W=W*∪{0}, 其中 W*={u|u∈W1,p0(Ω),a(u)-b(u)>0, J(u) 令 N={u∈W1,p0(Ω)|I(u)=0,‖u‖p1,p(Ω)≠0}, W={u∈W1,p0(Ω)|I(u)>0, J(u) V={u∈W1,p0(Ω)|I(u)<0,J(u) 下面引入一势井族.对δ>0,定义 Iδ(u)=δa(u)-b(u), Nδ={u∈W1,p0(Ω)|Iδ(u)>0, J(u) Wδ={u∈W1,p0(Ω)|Iδ(u)>0, J(u) Vδ={u∈W1,p0(Ω)|Iδ(u)<0,J(u) 下面给出势井族的相关结论. 1) 若0<‖u‖1,p(Ω) 2) 若Iδ(u)<0,则‖u‖1,p(Ω)>r(δ).特别地,若I(u)<0,则‖u‖1,p(Ω)>r(1). 3) 若Iδ(u)=0,则‖u‖1,p(Ω)≥r(δ)或‖u‖1,p(Ω)=0,特别地,若I(u)=0,则‖u‖1,p(Ω)≥r(1),或‖u‖1,p(Ω)=0. 证明1)的证明.由0<‖u‖1,p(Ω) Iδ(u)=δ‖u‖p1,p(Ω)-‖u‖2+α2+α(Ω)≥ δ‖u‖p1,p(Ω)-C1+α*‖u‖2+α1,p(Ω)≥ ‖u‖p1,p(Ω)(δ-C1+α*‖u‖2+α-p1,p(Ω))>0, 由Iδ(u)的定义,1)得证. 2)的证明.由Iδ(u)<0,有 0>δ‖u‖p1,p(Ω)-‖u‖2+α2+α(Ω)≥ δ‖u‖p1,p(Ω)-C1+α*‖u‖2+α1,p(Ω)≥ ‖u‖p1,p(Ω)(δ-C1+α*‖u‖2+α-p1,p(Ω)), 得‖u‖1,p(Ω)>r(δ). 3)的证明.若Iδ(u)=0,且‖u‖1,p(Ω)≠0,则有 δ‖u‖p1,p(Ω)-‖u‖2+α2+α(Ω)≥ δ‖u‖p1,p(Ω)-C1+α*‖u‖2+α1,p(Ω)= ‖u‖p1,p(Ω)(δ-C1+α*‖u‖2+α-p1,p(Ω))=0, 得‖u‖1,p(Ω)≥r(δ). 4)的证明.由引理1.3的3)和 下面给出d(δ)的相关结论. 引理 1.42+α>p,p>2,d(δ)满足下列性质: 证明1)u∈N,则由引理1.3的3)可得‖u‖1,p(Ω)≥r(δ),从而由 c(δ)rp(δ)≥c(δ)r2(δ), 得到d(δ)≥c(δ)r2(δ). 使得Iδ(λu)=0.从而λu∈Nδ,且 J(v) 事实上,由引理1.4的2)得 Iδ(λ(δ)u)=0,λ(δ″)=1. 令g(λ)=J(λu),得 (1-δ)λp-1‖u‖p1,p(Ω), J(v)-J(u)=g(1)-g(λ(δ′))≥ (1-δ″)λp-1(δ′)rp(δ″)(λ(δ″)-λ(δ′))= ε(δ′,δ″)>0. J(u)-J(v)≥ (δ″-1)λp-1(δ″)rp(δ″)(λ(δ′)-λ(δ″))= ε(δ′,δ″)>0. 现定义 由引理1.4,d0≥0. 下面研究Iδ(u)的不变号性. 弱解的整体存在性需要分情况来讨论.本节先讨论p>2+α时的情形,下节再讨论p<2+α时的情形. u∈L∞([0,T];W1,p0(Ω)), (8) ut∈L2([0,T];L2(Ω)). (9) 若n 若在Ω内几乎处处有u0(x)≥0,则对任一固定的t≥0,u(x,t)≥0在Ω内几乎处处成立,并且此时u(x,t)是问题(1)~(3)的解. 证明令 m=1,2,…,n (10) 满足 (φ(um(t)),ωj), 1≤j≤m, (11) (12) 在W1,p0(Ω)内,其中 (13) 由Sobolev嵌入定理及Young不等式得 由此可得 由这两个估计及Aubin紧性引理知,存在函数u及{um}的子序列{uμ},使得 uμ(T)→u(T)于W1,p0(Ω)弱收敛, uμ→u于L2+α([0,T];L2+α(Ω))弱收敛, Auμ→Au于L([0,T];W-1,p(p-1)(Ω))弱*收敛.(14) 这就说明u是问题(1)~(3)的解. 下面证明问题(1)~(3)的弱解是唯一的.事实上,设u1与u2是问题(1)~(3)的两个解.记ω=u1-u2,则ω满足 其中 在方程(11)两端对ω作内积,并利用A的单调性与Sobolev嵌入定理,可得 下面证明解的保号性,即当u0≥0时,u≥0.记 V([0,T];W1,p0(Ω))={v(t)∈L2([0,T]; W1,p0(Ω)),v′(t)∈L2(Ω)}, 用任意C1类函数f(t)乘(11)式并在[0,t]上积分,得 取m=μ(即以{um}中的收敛子列代替{um}),固定j,并令μ→∞取极限得 这说明 ∀ψ∈V([0,T];W1,p0(Ω)). (16) 特别地,取ψ(s)=v(s)-u(s),其中v(s)=sup{u(s),0},则有 由v(s)的定义和(16)式可得 (Av-Au,v-u)≥0. 故 (17) 从而,若u0(x)≥0在Ω内几乎处处成立,则(17)式右边恒为0,左端几乎处处为0,v(t)又是u(t)的正部.可得:当t≥0时,有u(x,t)≥0在Ω内几乎处处成立. u∈L∞([0,T];W1,p0(Ω)), ut∈L2([0,T];L2(Ω)), 及 ‖u(t)‖L2(Ω)≤‖u(s)‖L2(Ω), t≥s≥0. (18) 若几乎处处在Ω内有u0(x)≥0,则对任意固定的t>0,u(x,t)≥0几乎处处在Ω内成立.从而u(x,t)≥0是问题(1)~(3)的解. 证明再一次使用Galerkin方法.{ωi}及um的意义见定理2.1的证明.设 {u0m}⊂W, (19) 在W1,p0(Ω)内,由常微分方程的存在性定理知,存在tm>0,使得在[0,tm]内(11)式有解um(t),并且(13)式成立,即 J(um)≤J(u0m),t∈[0,tm]. (20) 证明 um(t)∈W, ∀t≥0. (21) 假设(21)式不成立,以t*表示使um(t*)∉W的最小的时间.由连续性知um(t*)∈∂W,故由引理1.4得 J(um(t*))=d, (22) 或 a(um(t*))-b(um(t*))=0. (23) 若(22)式成立,这与(20)式及u0m∈W相矛盾.若(23)式成立,则 也得到同样的矛盾,说明(21)式成立. 从(20)式及引理1.2得 J(u0m(t))≤C. 由此得 ‖um‖L∞([0,T];W1,p0(Ω))≤C, 利用Aubin紧性定理及单调算子理论可知,存在函数u及{um}的子序列{uμ}使(14)式成立,故u是(1)~(3)的解. a(u(t))-b(u(t))≥0. (24) 另一方面,在(16)式中取ψ(s)=u(s),不难得到 (25) 由(24)及(25)式立得(16)式. 本定理的其他结论与定理2.1的一些证明过程类似可得. 先建立问题(1)~(3)的解的不变集合. Iδ(u0)=(δ-1)‖u‖p1,p(Ω)+I(u0)>0, 将(1)式乘以ut,并在Ω×[0,t)上分别积分, (26) Iδ(u(t0))=0, ‖u(t0)‖1,p(Ω)≠0, 或J(u0)=d(δ). 由命题4.1,J(u0) 2)J(u0)=d(δ),I(u0)<0时,令u=u(x,t)是(1)~(3)的弱解,T是u的最大存在时间. 如果不成立,则存在t0∈(0,T),使得当0≤t u(x,t)∈Vδ,u(x,t0)∈V. 因此,存在 由(26)式,J(u(t0))=d(δ)不成立. 若0 ‖u‖1,p(Ω)≥r(δ), 0 由d(δ)的定义,得J(u(t0))≥d(δ),这也与(26)式矛盾. 1) 当I(u0)>0时,对任意δ1<δ<δ2,有u∈Wδ; 2) 当I(u0)<0时,对任意δ1<δ<δ2,有u∈Vδ. 证明1) 因为I(u0)>0,且Iδ(u)的符号在δ1<δ<δ2上不变,则有 Iδ(u0)>0,δ∈(δ1,δ2). 另一方面,由引理1.4和能量公式 J(u0)=d(δ1)= d(δ2) (27) 已知J(u0) 2) 由引理1.5和I(u0)<0,得 Iδ(u0)<0,δ∈(δ1,δ2). 另一方面,能量公式(27)和 0 表明J(u0) u∈Vδ,δ1<δ<δ2. 余下的证明与命题4.1的2)中的证明类似. 推论 4.2若将推论4.1中的假设J(u0)=σ换成0 结果是,若0 推论4.1和推论4.2的结果表明,0 Uσ={u∈W1,p0(Ω)|‖u‖p1,p(Ω)≠0, Iδ(u0)=0,δ1<δ<δ2}, 使得问题(1)~(3)在Uσ内只有零解. 随着σ的减小,真空区Uσ变得越来越大,即若σ1<σ2,Uσ2 注 4.2如下图,在整个区域W内方程有解,在Uσ区域内只有零解,把这个现象称为真空隔离现象. 为了处理其他情况,有下面的命题. 1)I(u0)>0时,对所有0≤t 2)I(u0)<0时,对所有0≤t 其中T是u(x,t)的最大存在时间. 证明 1) 若结论不成立,则存在t1∈(0,T),使得对所有0 I(u(t1))=0,I(u(t))>0. 然后结合 I(u)=-(u′,u)-(∇u′,∇u)≠0, 对所有0 (28) 对所有0 2) 若结论不成立,则存在t1∈(0,T),使得对所有0 I(u(t1))=0,I(u(t))>0. 类似1)的证明,对所有0 J(u)=J(u0)- (29) 同样,由引理1.3和0≤t 现在来讨论问题(1)~(3)的解的爆破.首先给出解在+∞处爆破的定义. 定义 5.1(在+∞处的爆破) 设u(x,t)是问题(1)~(3)的弱解,若解的最大存在时间T=+∞,且 则u(x,t)在+∞处爆破. 证明因为使用常用的凸算子方法和反证法未得到方程组的弱解在有限处有关爆破的相关结论,所以本章暂研究问题(1)~(3)的解在+∞处产生爆破的问题. 令 则当t>0时,有 G″(t)=-2I(u(t))>0. 事实上,由J(u)、I(u)定义得 J(u)= (30) 因为I(u)<0,所以由Sobolev嵌入定理得 (31) 利用(28)、(30)和(31)式得 G″(t)=-2pJ(u)+ (32) 因此,对所有t≥0,有 (33) 表明u(x,t)在+∞处爆破.因为 利用(32)和(33)式,得 G(t)G″(t)-(G′(t))2=[-2p(J(u0)- 上面的不等式可以由Hölder不等式推出,且 因此,对任意0<α2<1,有 G(t)G″(t)-α2(G′(t))2≥ 由(33)式知,存在t1>0,使得 G(t)G″(t)-α2(G′(t))2>0,t≥t1, 则可得 (G(t)1-α2)′=(1-α2)G(t)-α2G′(t), (G(t)1-α2)″=(1-α2)G(t)-α2-1× [-α2(G′(t))2+G(t)G″(t)]≥0. 令tα2≥t1,且满足G(tα2)>0,则 且 其中 由G″(t)>0,有 对任意0<α2<1,从而对所有t≥tα2,有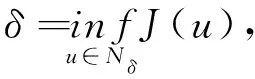

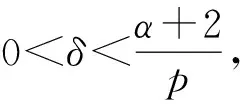
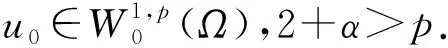
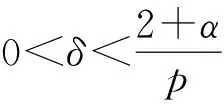

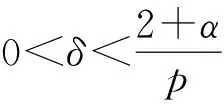
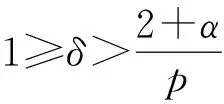

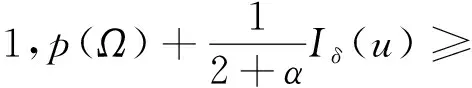
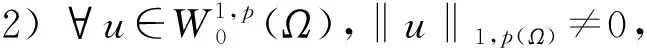
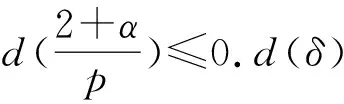

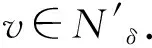


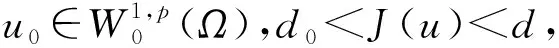
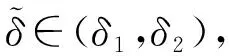
2 p>2+α时的整体存在性和唯一性
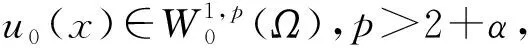

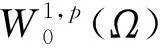
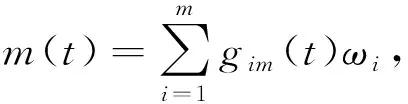

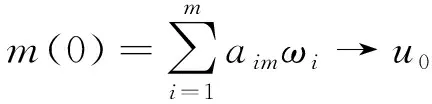
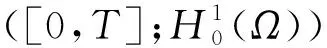
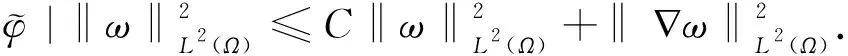
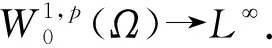
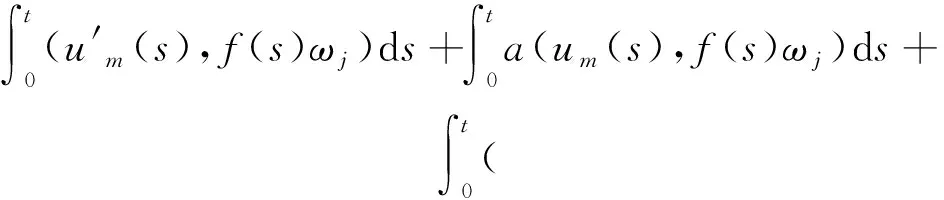
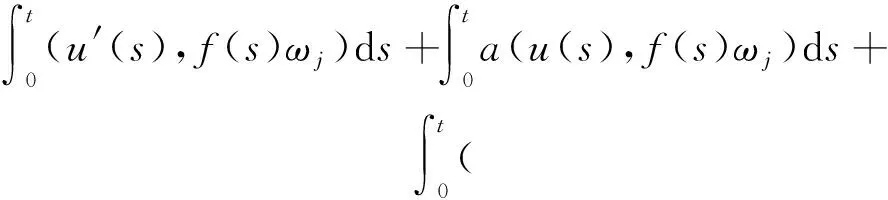
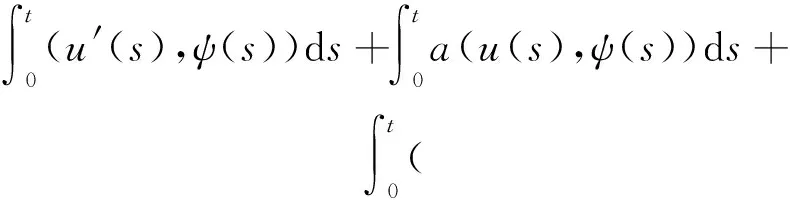
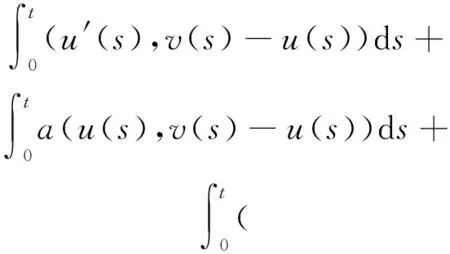
3 p<2+α时的整体存在性
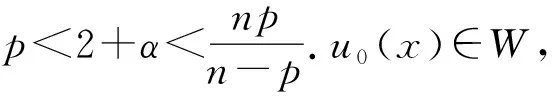
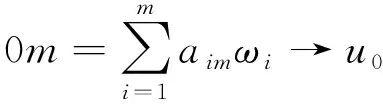
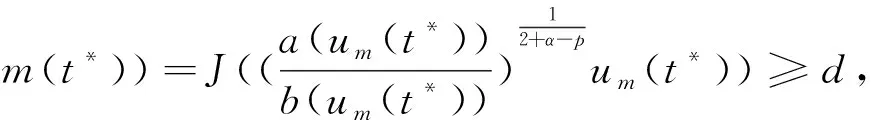
4 解的真空隔离
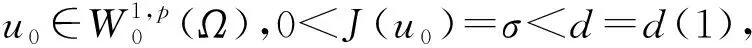


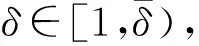
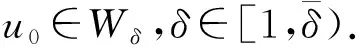
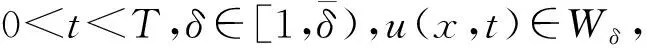
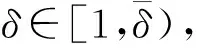

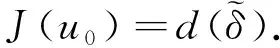


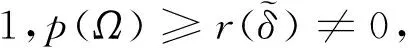
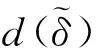
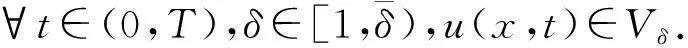
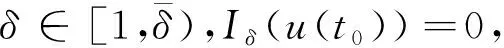
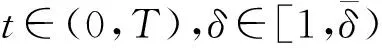
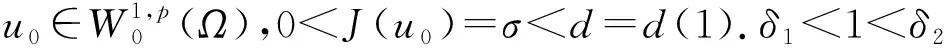

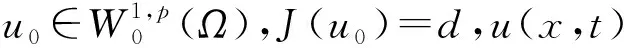
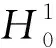
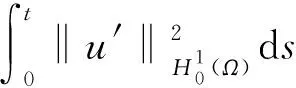
5 爆破现象