改进布谷鸟算法求解有限缓冲区批量流水调度问题

彭 菁，段 程，李益兵

(武汉理工大学 机电工程学院,湖北 武汉 430070)

有限缓冲批量调度问题是基于批量流水线调度提出的一类问题：每个加工批次在一台机器上完工后，先进入缓冲区暂存，等到下台机器空余时，再进入下一道工序进行加工，否则会发生阻塞。目前对于批量调度问题的研究约束条件越来越复杂，其中采用有限缓冲批量调度方式能够更加贴近实际存储设备的约束下的生产环境，进而解决决策目标。因此，关于有限缓冲批量流水车间调度问题(limited buffer flow shop scheduling problem，LBFSSP)的研究具备学术价值以及实际意义。

目前，已有多种方法被应用于研究批量流水线调度问题，如遗传算法、粒子群算法、蚁群算法、人工蜂群算法、和声算法和布谷鸟算法等[1-6]，这些算法在一定程度上取得了较好的效果。

随着对流水线调度问题不断地深入研究，针对存在有限缓冲区的流水线调度问题，学者提出各种智能优化算法来解决。其中，张培文[7]提出有效的混合人工蜂群算法，结合WPFE(weighted profile fitting based on NEH)启发式算法和遗传算法改进人工蜂群算法，用来解决最大完工时间为目标的有限缓冲区流水车间调度问题。韩玉艳[8]采用离散NSGA(non-dominated sorting genetic algorithm)-Ⅱ算法进化求解带有限缓冲区的多目标批量流水线调度问题，所提算法充分利用非支配解的信息引导种群进化。Liang[9]设计了一种自适应差分进化算法(differential evolution,DE)，用于解决有限缓冲区的多目标流水车间调度问题。

由于在零等待和零空闲的批量流水车间的问题方面，等批量划分方式比一致子批划分策略所获得的最大完工时间更短[10]，大部分文献对批量流水线问题的研究建立在等量分批且批量划分方案已知的模型上，而缺乏对非等量分批调度问题的探究。针对有限缓冲区的批量调度问题，笔者基于批量划分方案未知且非等量分批的分批方式，以总的提前惩罚和延期惩罚为评价指标建立了针对存在有限缓冲区的一致子批[11]调度模型，并使用改进算法验证了相应结果。

1 改进布谷鸟算法

1.1 标准布谷鸟算法

布谷鸟搜索算法(cuckoo search algorithm，CS)是基于对布谷鸟寻窝产卵的行为进行模拟，以此提出了一种全新的搜索算法。该算法具有简单、参数少、高效等优点，并且多次成功应用于工程优化问题中，逐渐在群智能算法领域中崭露头角[12]。

布谷鸟算法模拟了布谷鸟为寻找适合的产卵鸟巢而随机游走的寻窝过程。算法设定3个理想条件作为基础：①布谷鸟每次随机选择一个鸟窝来产卵，每次只产一个卵；②在所有的鸟窝中，适应度最好的鸟巢会保留到下一代；③每代产生的鸟巢数量是一定的，其中布谷鸟卵被发现的概率为Pα。在上述3个理想状态的基础上，算法产生新的候选解的更新公式:

(1)

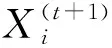
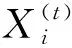
1.2 编码规则的设计

标准布谷鸟搜索算法的编码方式是连续的，而流水线车间的调度问题是离散的，因此，首先需要将布谷鸟的连续编码进行离散化，如图1所示。

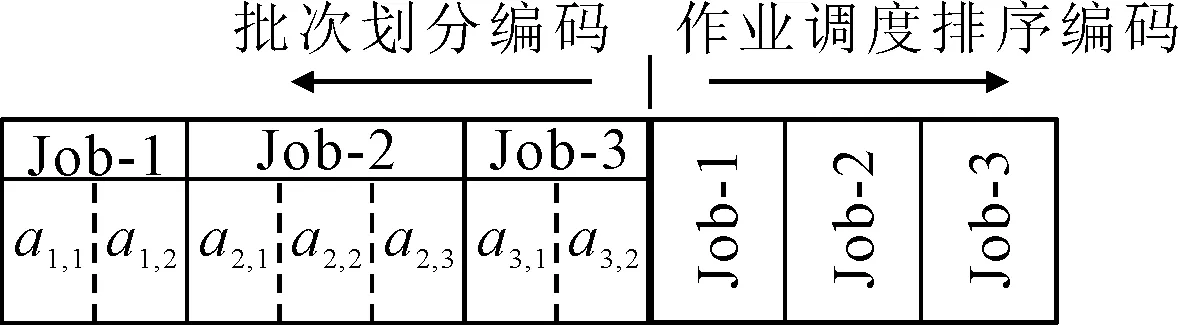
图1 编码规则

在编码模型中，每一维表示一个鸟巢，每个鸟巢将编码分为两段[10]，前一段编码将每个加工批次分成多个不等量的子批次，后一段用来给作业批次排序。

1.3 动态适应的淘汰概率

标准布谷鸟算法中，种群通过莱维飞行产生新解后，种群当中的每个解都会产生随机值，与淘汰概率Pα相比，如果随机数大于淘汰概率，则保留该解，如果随机数小于淘汰概率，则对这部分解淘汰并产生新解。随着迭代次数Giter的增加，后期解的变化会变得不明显，容易陷入局部最优。因此参考文献[13-14]，设计了一个动态适应的淘汰概率来替代固定的淘汰概率。

(2)

式中:Pmax为设定的最大淘汰概率；Gmax为设定的最大迭代次数。

通过动态适应的淘汰机制，算法前期以较小概率搜索种群，提高搜索效率，在后期以较大概率更新种群，加快收敛速度，提升算法性能。

1.4 基于关键路径的局部搜索

关键路径是指对某一特定的加工顺序中决定最大完工时间的作业批次的序列，而每一个批次的加工时长被称为关键块。关键路径上任何操作的变化都是影响最大完工时间的关键因素，也是构建邻域结构的重要因素。因此，针对布谷鸟算法存在后期收敛速度慢、局部搜索能力弱和易早熟收敛等缺点，在调度顺序确定的情况下改变子批量的分批数量，避免算法陷入局部最优，从而获得更优解。

1.4.1 分批数目的局部搜索

首先要确定关键路径，统计各个子批次在每个工序开始加工之前的阻塞时间，选择阻塞时间最长的子批次作为局部搜索的关键批次。

如图2所示，以3个作业批次为例，每个作业批次均分作2个子批次。图2中阴影是有限缓冲区约束导致的子批次阻塞，加粗的黑色子批次块所组成的路径是关键路径。

图2 关键路径的两种领域结构

局部搜索策略基于关键路径的两种邻域结构N1、N2，具体解释如下：

N1：如果关键块内的首个子批次和下个子批次是同一作业批次，则首个批次与下一个子批次互换；关键块的末子批次如果和上一个批次是同一作业批次，则末子批次和上一个子批次互换。这种领域结构能够改变关键块的生产顺序从而有机会缩小生产阻塞。

N2：关键块的首个子批次在分批次范围允许的情况下，将首个子批次均等分成两个子批次。这种邻域结构通过改变关键块的大小来改变关键路径的生产状况。

1.4.2 调度排序的局部搜索

首先明确作业批次调度的关键作业批次。统计各个作业批次停滞在机器上的非加工时间的长短，选择阻塞时间最长的作业批次作为关键作业批次。局部搜索[2,8]的方式如图3所示，K1和K2分别指代编码上两个不同位置的标志。以10个作业批次为例，交换机制指的是在确定关键作业批次在调度序列中的位置值K1后，另外选择在除关键作业批次外的位置随机产生一个位置值K2，然后交换它们位置上的编码。插入机制指的是在调度排序部分之间随机产生一个位置K2，将K1位置的关键作业批次编码插入到K2位置之前，形成新解。

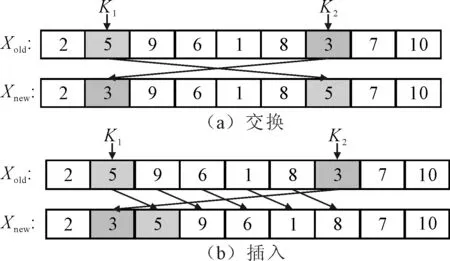
图3 局部搜索的两种方式

2 数据仿真与分析

以某医疗器械公司实际工况下的批量流水车间调度问题为研究对象，每批工件的加工总数和最大分批数目、缓冲区最大存储区数目如表1所示，另外，每个作业批次在每台机器上的加工时间如表2所示。

表1 每批作业批次工件总数、最大分批数和缓冲区最大存储工件数

表2 作业批次与相应工序加工时长的关系 min

测试案例在双核CPU主频1.8 GHz，内存为8 GB，处理器为intel(R)Core(TM)i5-3337U，操作系统为Window8，开发环境为MatlabR2016b的电脑上运行。

参考文献[5]，算法的相关参数设置如表3所示。另外，在引入的基于关键路径的局部搜索机制中，局部搜索产生的概率为0.1。作业批次数目n分别为3、5、7，机器数目分别为3、5、7，已设置一定权重的提前惩罚和延期惩罚作为评价算法的标准。

表3 算法参数设置

通过实验模拟，改进前后的布谷鸟算法执行10次后的结果如表4所示。改进前后布谷鸟算法评价目标的箱线图如图4所示。

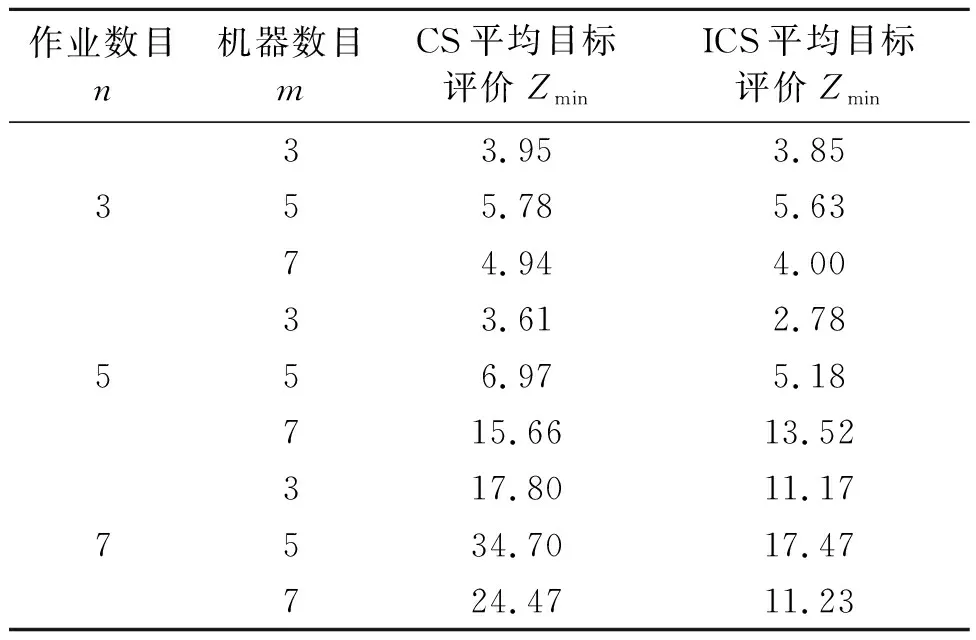
表4 标准布谷鸟算法(CS)和改进后布谷鸟算法(ICS)结果比较

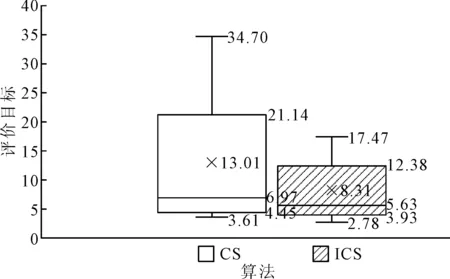
图4 改进前后布谷鸟算法评价目标的箱线图

从表4可知，改进布谷鸟算法得到的最优评价目标的均值小于标准布谷鸟算法，证明了改进布谷鸟算法可得到更优的目标解。

由图4可知，改进后布谷鸟的四分位间距几乎是改进前的一半，证明求解的评价目标数值更加集中。改进前布谷鸟算法有50%的解的评价目标小于6.97，而改进算法有50%的解小于5.63，评价目标降低了19.2%。并且未改进算法75%的解的评价目标小于21.14，而改进后算法75%的解的评价目标小于12.38，评价目标降低了41.4%，证明该优化算法普遍获得了更优解，并且解的范围更加集中，算法的质量得到了明显改善。

3 结论

笔者考虑了大批量流水车间的实际生产状况，构建了存在有限缓冲区的批量流水车间模型，模型采用一致子批的分批方式，综合考虑了提前评价和延期评价作为目标函数。另外，在标准布谷鸟搜索算法的基础上，提出一种动态的淘汰机制来替代不变的淘汰概率，优化了算法的搜索策略，又引入基于关键路径的局部搜索，能够高效地获得更优解。仿真实验和算法比较结果显示，改进后的布谷鸟算法比标准布谷鸟算法具有更优秀的综合能力，在收敛速度和寻优能力两方面都更出色。该结果也表明，所研究的改进布谷鸟算法在解决存在有限缓冲区的流水车间调度问题上具有明显优势。