精密数控机床进给系统有限元分析

尹 鹏，郑银环，秦信春

(武汉理工大学 机电工程学院，湖北 武汉 430070)

随着科技的不断进步，对零件加工精度、加工工艺和效率的要求越来越高，精密数控机床的加工精度及整体性能取决于机床的各个方向上的进给系统，研究精密数控机床进给系统静动态特性，对其进行动力学优化分析，从而提高机床的精密性，这是十分必要的。

针对精密数控机床进给系统仿真优化分析问题，国内外学者做了很多工作，罗亮等[1]提出了一种改进的集中质量建模方法，该方法考虑了滚珠丝杠进给系统基座的质量、柔性及进给系统部件间反向间隙对系统动态特性的影响，并完善了滚珠丝杠进给系统集中质量模型等效参数的计算方法，其不足在于未能充分考虑进给系统温度场热特性影响。Huang[2]对机床进给系统的热源进行了分析，提出了一种进给系统的热变形预测模型，并用实验对模型进行验证。李醒飞等[3]提出了一种引入温度变化参数来修正滚珠丝杠的温度场热误差预测模型，并以温度分布实验对该模型进行验证。

在机床实际工作中，进给系统受到力和热的共同作用，为了能全面准确地反映进给系统的静动态特性，笔者对进给系统在结构场与温度场共同作用下进行建模分析，建立进给系统热-结构耦合场有限元模型，并对其进行静力学分析、模态及谐响应分析，结合所分析的结果，分析出进给系统中的薄弱环节并给出相应的改善建议。

1 进给系统等效模型建立

1.1 进给系统基本结构

刀架X方向进给系统在工作过程中承受各种切削力，其在实际工作中承受的载荷最大。刀架X方向进给系统的结构设计带来的进给误差及振动直接影响其切削进给运动的精度及稳定性，最终影响加工零件的尺寸精度及表面粗糙度。因此，选取刀架系统X方向进给系统进行建模及分析, 刀架X方向进给系统结构如图1所示。

图1 刀架进给系统结构示意图

1.2 进给系统结合部等效刚度和阻尼计算

1.2.1 固定结合部等效刚度和阻尼计算

依据“吉村允孝法”，通过计算固定结合部上的接触压力得到固定结合部单位面积的刚度和阻尼，再利用结合面积积分法计算出各结合部的等效刚度和等效阻尼[4]，计算结果如表1所示。

表1 固定结合部的刚度和阻尼

1.2.2 滚动结合部等效刚度计算

进给系统直线导轨副的结构及受力如图2所示，其中滚珠总数为z，滚珠与滚道接触压力角为β，滑块受到从托板上传递过来外部法向载荷Fz的作用，单个滚珠施加到导轨及滚道的法向作用力为Fn1、Fn2、Fn3和Fn4。根据直线导轨副结合部的受力对称性，有Fn1=Fn2，Fn3=Fn4。由导轨副结合部在竖直方向上受力平衡得：

Fz+z·Fn3sinβ=z·Fn1sinβ

(1)

图2 直线导轨滑块结构受力图

依据Hertz接触理论，所有滚珠承载的预紧力F0近似均匀分布，同时滚珠与滚道接触点之间的法向压力均为P0，由预紧力F0引起单个滚珠的初始变形量均为δ0，F0与P0之间关系为：

(2)

当导轨副上受外载荷Fz作用时，上下排滚珠的变形量分别为δ1、δ2，同时滑块竖直方向的位移为δn，则结合部变形协调方程为：

(δ1-δ0)sinβ=(δ0-δ2)sinβ=δn

(3)

根据Hertz接触理论，上下排滚珠的变形量δ1、δ2为：

(4)

式中：K、a为Hertz系数；u1、u2分别为滚珠与导轨滑块的泊松比；E1、E2分别为滚珠与导轨滑块的弹性模量；∑ρ为滚珠与导轨滑块的接触点处的综合曲率；Q为导轨及滚道受到滚珠的施加法向载荷。

联立式(2)～式(4)可求得δ0、δ1、δ2，可得导轨滑块结合部的法向刚度为：

Kn=F/δn

(5)

式中，F为法向外载荷。

滑块相对于导轨的切向位移为：

δT=(δn-δ0)cosβ

(6)

则导轨滑块结合部的切向刚度为：

(7)

进给系统中滚珠直径d为6.87 mm;接触角β为45°；z为48；F0为3 kN。滚动导轨副结合部刚度如表2所示。

表2 滚动导轨副的基本参数及刚度参数

1.3 进给系统热边界条件计算

进给系统在工作时的热源主要有：①伺服电机驱动发热Q1；②滚动轴承的摩擦生热Q2；③丝杠螺母副的摩擦生热Q3；④导轨滑块副的摩擦生热Q4。

1.3.1 伺服电机热流密度计算

电机的发热量Q1[5]为：

(8)

式中：η为伺服电机的工作效率；Mm为输出力矩；n为伺服电机的转速；α为伺服电机的发热量修正系数，通常情况下取α=0.3。

伺服电机的基本参数和计算所得热流密度如表3所示。

表3 伺服电机的基本参数和热流密度

1.3.2 轴承热流密度计算

采用Palmgren经验公式[6]计算轴承的单位时间发热量Q2为：

(9)

式中：nz为轴承转速；M1为与轴承负载有关的摩擦力矩；Mv为与轴承类型、转速及润滑性质有关的黏性摩擦力矩。

M1可按式(10)计算：

M1=fFβdm

(10)

式中：f为与载荷及轴承类型有关的系数；dm为轴承中径；Fβ为轴承摩擦力矩的计算载荷。

Mv可按式(11)计算：

(11)

式中：f0为与轴承类型和润滑方式有关的经验常数；v0为工作温度下润滑剂的运动黏度。

轴承基本参数和计算热流密度如表4所示[7]。

表4 轴承的基本参数和热流密度

1.3.3 丝杠螺母热流密度计算

滚珠丝杠的单位时间发热量Q3[5]为：

Q3=1.047×10-4Mn

(12)

式中：M为滚珠丝杠的摩擦力矩；n为滚珠丝杠的转速。

滚珠丝杠中的总摩擦力矩M按式(13)计算：

M=2Z(Me+Mg)cosβ

(13)

式中:Z为滚珠数目；Me为摩擦阻力矩；Mg为几何滑移摩擦力矩；β为丝杠的螺旋角度。

分别对摩擦力矩Me和几何滑移摩擦力矩Mg进行计算：

(14)

(15)

式中：μ，v为由滚珠与滚道的接触尺寸决定的系数；∑ρ为各主曲率之和；E1、E2分别为丝杆和螺母的弹性模量；F0为单个滚珠所受的法向力；R为滚道和滚珠的综合曲率半径。

滚珠丝杠的基本参数和计算所得热流密度如表5所示。

表5 滚珠丝杠基本参数和热流密度

1.3.4 导轨滑块热流密度的计算

导轨滑块副的单位发热量Q4[5]为：

(16)

式中：μ为动摩擦系数，μ=0.004；F为施加在单个导轨摩擦面上的负载，具体见表2；v为滑块在导轨上滑动速度，v=0.4 m/s；J为热功当量，J=4.2 J/cal。

计算所得导轨滑块副热流密度如表6所示。

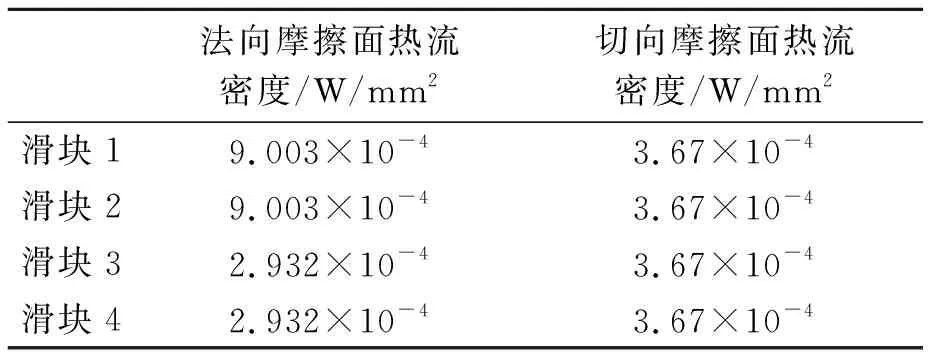
表6 滑块的热流密度

2 进给系统热-结构耦合有限元模型建立

在Solidworks中建立进给系统的三维模型，并对模型进行适当简化，导入到ANSYS Workbench平台，利用Workbench中Transient Thermal、Static Structural、Modal和Harmonic Response模块建立进给系统热-结构耦合有限元模型，具体过程如下：

(1)为了减少仿真计算量，提高分析精度和效率，忽略零件部分工艺，将实体模型中对仿真结果影响较小的地方做适当的简化，简化后结构如图3所示。

图3 进给系统三维模型简化图

(2)采用Workbench中Hex Dominant(六面体主体法)进行网格划分，对进给系统结构有限元模型中各零件进行材料属性设置，如表7所示。

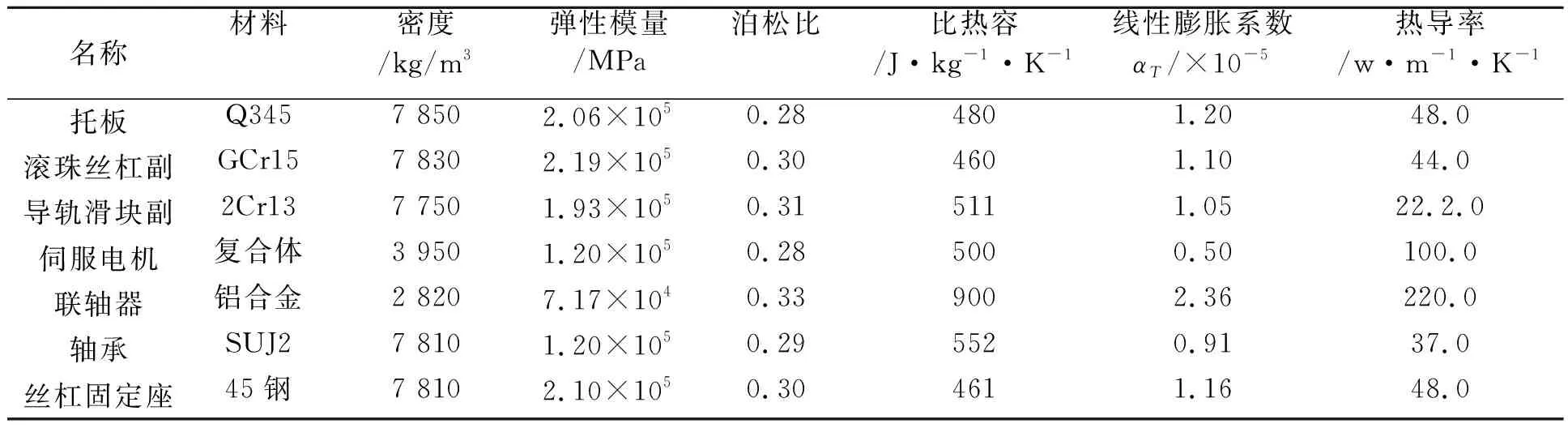
表7 材料参数表

(3)进给系统结合部等效建模。根据计算得到的结合部刚度阻尼参数，使用ANSYS Workbench中接触设置Spring功能建立固定结合部等效刚度阻尼模型和滚动结合部的等效刚度模型[8-9]。

(4)根据所计算的热边界条件，在Harmonic Response模块完成进给系统有限元模型热边界条件设定。

(5)结构场边界条件设定。将刀架系统上其他部件进行简化，作为一个分布式质量单元添加到刀架托板上。对导轨、轴承座及电机固定座实施固定约束，添加沿Y轴负方向的重力加速度、丝杠预紧力及各方向上最大工作载荷，约束及载荷施加情况如图4所示。

图4 进给系统的约束及载荷施加

3 进给系统静力学分析

根据建立的进给系统热-结构耦合有限元模型，得到进给系统的变形与等效应力如图5、图6所示。

图5 进给系统的变形云图

图6 进给系统等效应力云图

由图5可知，进给系统的丝杠和导轨上的总变形量很小，主要变形由托板底端向顶端呈现阶梯式增大，在靠近丝杠侧的顶端综合变形量最大为44.326 μm，整体变形呈现出了很强的不均匀性，其原因主要由于进给系统各处部位温升的不同及材料特性差异导致进给系统不同位置发生不均匀的热膨胀[10]，特别是在托板左侧有丝杠螺母发热带来热应力的影响，使得丝杠螺母附近变形偏大，同时使得左侧顶端的变形明显要大于右侧顶端。

由图6可知，系统整体应力分布比较均匀且基本在29.388 MPa的范围内，应力集中主要分布在丝杠两轴端与固定轴承接触处，这是由于两侧的固定轴承限制了滚珠丝杠热变形的自由膨胀，从而使丝杠两端受挤压产生了最大等效应力，该部位许用应力[σ]=345 MPa，满足强度要求。

4 进给系统模态分析

运用Workbench中的Modal模块进行模态分析，得到进给系统的前6阶振型数据和振型图如图7和表8所示。

从图7可知，进给系统各阶振型中变形区域均集中在托板上端及中间区域，且振幅变动不是很大，最大变形为11.54 mm，同时从各阶振型及对应的最大振幅可以看出，与X、Y方向的振动相比，托板上端，特别是两侧伸出端，更易在Z方向

图7 进给系统热—结构耦合模态振型图

表8 进给系统前6阶固有频率及振型

上发生较大振幅的振动，其原因在于托板顶端部分从Z向上看类似外伸梁结构，缺少固定支承，托板在X、Y方向上均有固定约束，因此相比X、Y方向更易因外部载荷施加产生较大变形及振动。总的来说，进给系统整体具有比较好的动刚度。

5 进给系统谐响应分析

采用Workbench中的Harmonic Response模块进行谐响应分析，基于所建立的热-结构耦合有限元模型，施加X、Y、Z3个方向上的切削力作为激振力和激振频率，将正弦扫频频率范围设定为0～800 Hz，步数设定为25步，得到进给系统在X、Y、Z3个方向上的幅频曲线图，如图8所示。

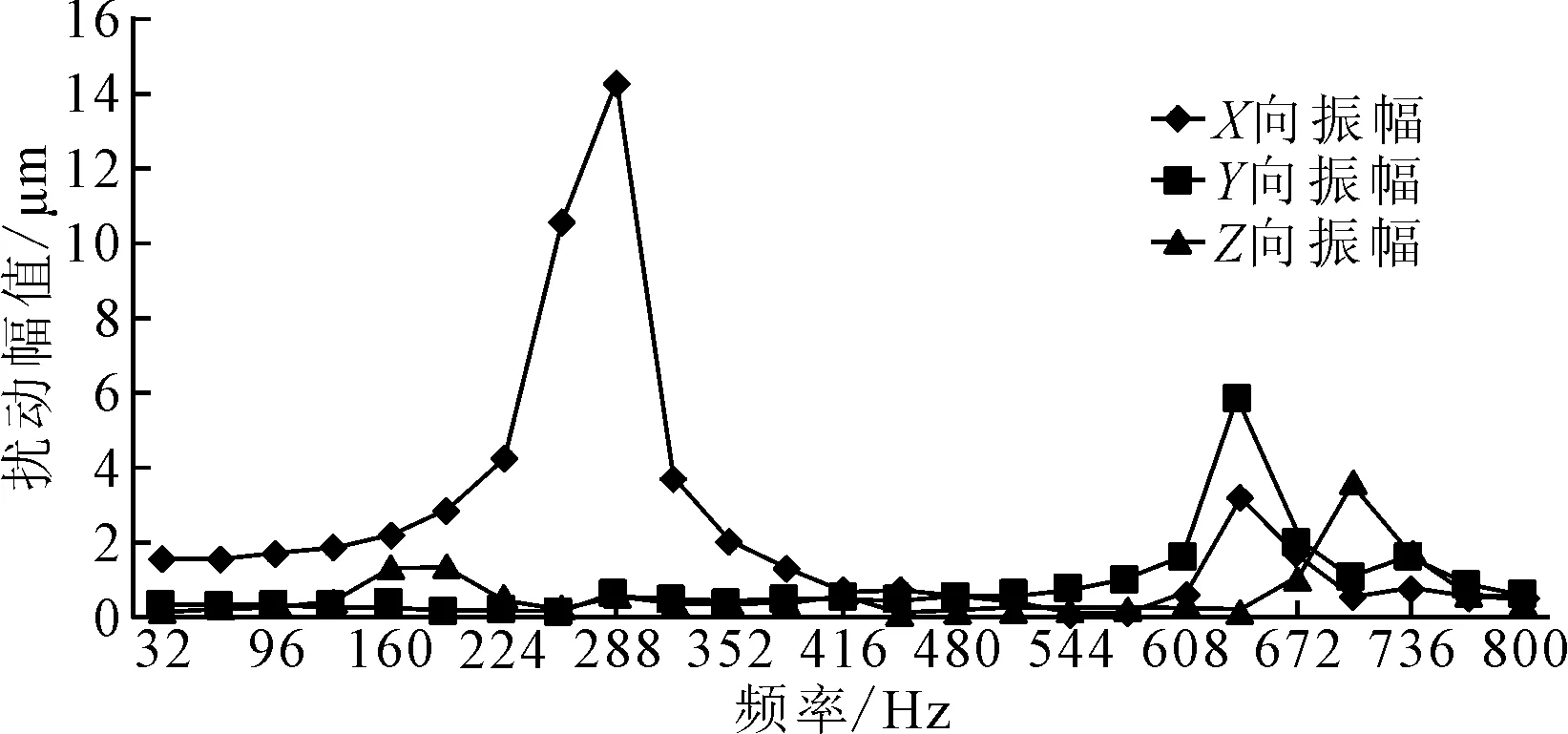
图8 进给系统幅频曲线图

从图8可知，当外界激励频率在288 Hz或640 Hz或690 Hz附近时，进给系统依次会在X、Y、Z方向上出现共振现象，且最大振幅接近15 μm，出现在X方向上，其余两个方向上的振幅均在6 μm范围内，这3处共振频率与模态分析得出的固有频率比较可知，进给系统本身不会出现这3个共振频率。但考虑到实际机床加工过程中，进给系统因工况不同需要在不同的转速及动载荷下进行工作时，易受到不可预知外界激励力的作用时出现共振。因此在实际加工过程中应通过调节相应转速及动载荷尽可能避免共振的出现。

6 结论

从受力分析及前四阶模态振型图可知，进给系统的主要变形集中在托板上端及两侧伸出端，其原因在于两侧伸出端受力时为悬臂梁模式，受外载荷时不能受到很好的支承，从而造成上端的振幅偏大。可以将上端导轨的布置位置上移，以提高系统的整体刚度和固有频率，达到减小系统振动的目的。

从图7中的第五、六阶模态振型图及图8可知，当受到高频激励时，托板上各处都易发生变形且3个方向的振幅会出现明显的增大。可以选用刚度较高的合金材料来避免变形及振动，在实际加工过程中应通过调节相应转速及动载荷尽可能避免共振的出现。

由于丝杠螺母发热点比较集中，导致丝杠螺母附近变形偏大，使得托板两侧变形不均匀，易降低托板的定位精度和抗振性，从而影响机床的加工精度。为减少丝杠螺母与导轨滑块之间的摩擦热量，可以在螺母和导轨上采用稀油润滑，保证丝杠和导轨的传动精度。