多目标多障碍路径规划的改进蚁群算法研究

程 鑫，张 帆，同军超，张卫超

(1.武汉理工大学 机电工程学院，湖北 武汉 430070；2.湖北省磁悬浮工程技术研究中心，湖北 武汉 430070)

印刷电路板(printed cricuit board，PCB)是电子元器件连接的载体，大大减小了布线和装配差错[1]。目前PCB板朝着高密度、多层数、高可靠性等方向发展，但也使得焊点的焊接越来越困难，寻找通过所有焊点的最优路径成为一个亟待解决的难题。

PCB板上存在多个目标焊点以及大电容等阻碍焊接的元件，若不进行路径规划，焊头可能与焊接工件上的障碍物相撞，导致焊头报废甚至危及员工安全。按照某种顺序在有障碍物的有限环境中，寻找焊头通过多个目标焊点的最优路径，且在运动过程中能安全、无障碍的绕过所有障碍物[2]。这个难题既要找到使总路程最短的路径，又要保证焊点与焊点之间路径的安全性，既涉及到多点路径规划问题，又涉及到焊点避障问题，是一个NP(non-deterministic polynomial,非确定性多项式)问题，对于这个难题的研究有着重要的理论研究价值和广泛的工程应用价值。

多点路径规划问题可归结为TSP(traveling salesman problem,旅行商问题)问题，在解决TSP问题上，目前使用的方法有蚁群算法、遗传算法、粒子群算法等。文献[3]中应用Matlab对蚁群算法和遗传算法求解TSP问题进行对比研究，发现无论城市个数多少、城市间距离远近，蚁群算法都优于遗传算法。文献[4]中设计了一种包含蚁群算法和改进PRM(probabilistic road map)算法的融合算法，可一次规划多个目标点的路径，但规划出来的路径具有随机性。文献[5]将蚁群算法与遗传算法和粒子群算法对比，蚁群算法可靠性高、适应性强、精确度高。文献[6]先计算点与点之间的最短安全距离，然后找到使总路径最短的顺序，最后进行点与点之间的路径规划，这种方法所找到的总路径不一定最短，且计算量较大。

笔者提出了一种改进的蚁群算法来解决在PCB板上焊点焊接最优路径的问题，先对焊头所处的工作环境进行建模，然后进行点与点之间的轨迹规划，得出点与点之间最短路径，最后将多点相互间的最短距离矩阵代入到TSP问题中，得到使总路径最短的顺序及最短路径的长度。

1 蚁群算法基本原理与环境建模

1.1 蚁群算法基本原理

蚁群算法其灵感来源于蚂蚁在寻找食物过程中发现最优路径的行为,具有分布计算、信息正反馈和启发式搜索的特征，其本质实际上是进化算法中的一种启发式全局优化算法[7]。在寻找食物的过程中蚂蚁会分泌大量信息素，信息素分泌的多少与路经长度成反比，而蚂蚁在选择路径时会根据状态转移概率以较大概率选择信息素多的路径[8]，随着大量蚂蚁个体不断搜索，最优路径上的信息素越来越多，而较长路径上的信息素会慢慢变少或消失，蚂蚁选择最优路径的概率越大，最终整个蚁群会找出一条最优路径。

图1表示蚂蚁在觅食过程中的3个过程，其中点A为蚂蚁蚁穴，点D为食物所在地，四边形BECF为蚁穴与食物之间的障碍物，蚂蚁若想获得食物，可随机选择路径BEC或BFC。如图1(b)所示，开始时，两条路径上都无信息素，在点A的蚂蚁随机选择路径，两条路径上蚂蚁数量相等。由于路径BFC比路径BEC长度要短一倍，一段时间后，选择路径BFC的蚂蚁比选择路径BEC多一倍，于是路径BFC上积累的信息素浓度是路径BEC上积累的信息素浓度的两倍，随着时间的推移，蚂蚁将以更大的概率选择路径BFC，最终所有的蚂蚁都会选择路径BFC到达食物目的地，如图1(c)所示。由此可见，蚂蚁觅食是一个正反馈过程。

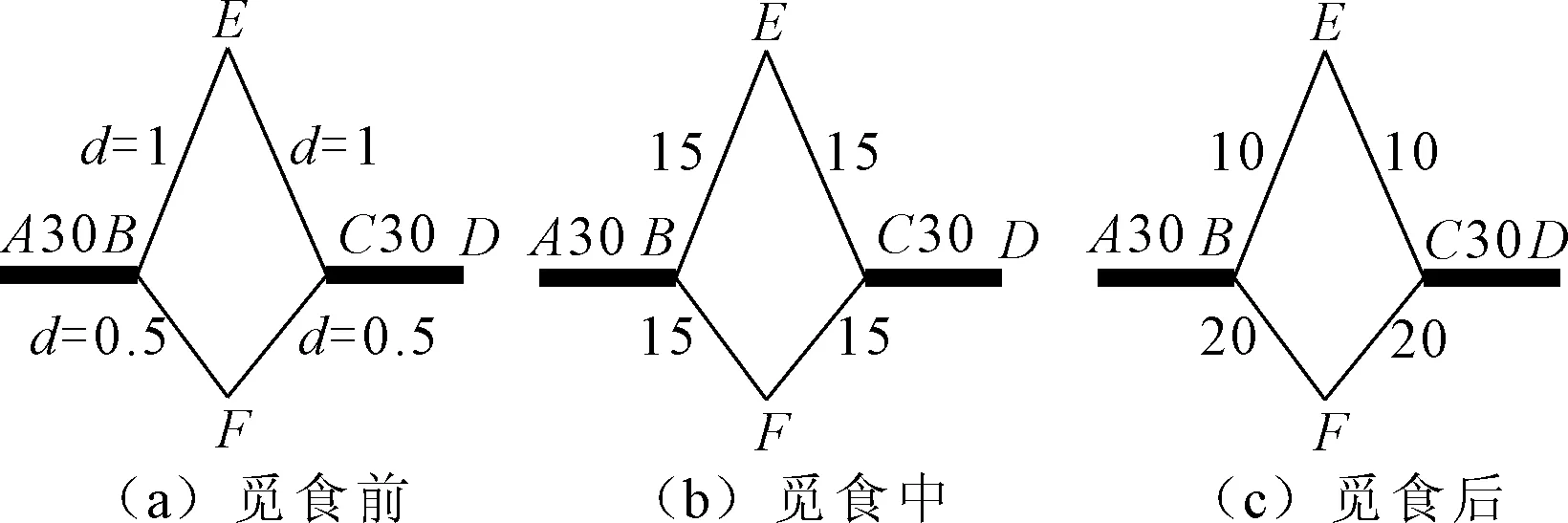
图1 蚂蚁觅食过程

1.2 环境建模

针对焊头的路径规划问题，焊头实际运行的工作环境是真实的物理空间，而用来路径规划的空间是虚拟空间，需要将物理空间转换成虚拟空间，抽象出能为建立模型起作用的机理，摒弃掉与建立模型无关的因素，这个环节称为环境建模[9]。环境建模是对焊头所处工作环境的有效描述，其质量好坏直接影响路径规划的复杂度以及后续算法性能的效率。

环境建模可以分为两类：基于网络或图的模型和基于栅格的模型[10]。基于网络或图的建模方法主要有顶点图像法、自由空间法、广义锥法，其模型精确度高，适用于对轨迹精度要求高的场合，但其模型建立计算量大，路径曲线控制难度大，应用于实际工程问题还需解决很多问题。基于栅格的模型建立简单，易在编程中实现，路径曲线易控制。笔者采用栅格法，假定焊头的空间信息已知，无障碍物的栅格为可行栅格，焊头可自由运动，有障碍物的栅格为不可行栅格，焊头需绕开障碍物运动。

对于栅格的标识方法有两种：直角坐标法和序号法。两者之间是可以相互转换的，其映射关系为：

(1)

式中：Xi为坐标的行；Yi为坐标的列；N为栅格序号；K为每行每列的栅格数；mod为取余，即取N/K的余数；int为取整，即取N/K的整数。

采用的工作环境栅格图如图2所示，假定工作环境为20×20的矩形区域，按从左向右、从上到下的顺序依次标记为1，2，…，400，每个序号代表一个栅格，令S={1，2，…，400}来表示栅格序列号，黑色栅格为障碍物，灰色栅格为目标焊点，白色栅格为可运行区域。为避免焊头与障碍物相撞，焊头当作质点忽略不计，障碍物不满一个栅格按一个栅格处理，且将障碍物向外膨胀，多占用一个栅格，使焊头能在规划好的路径中畅通无阻。

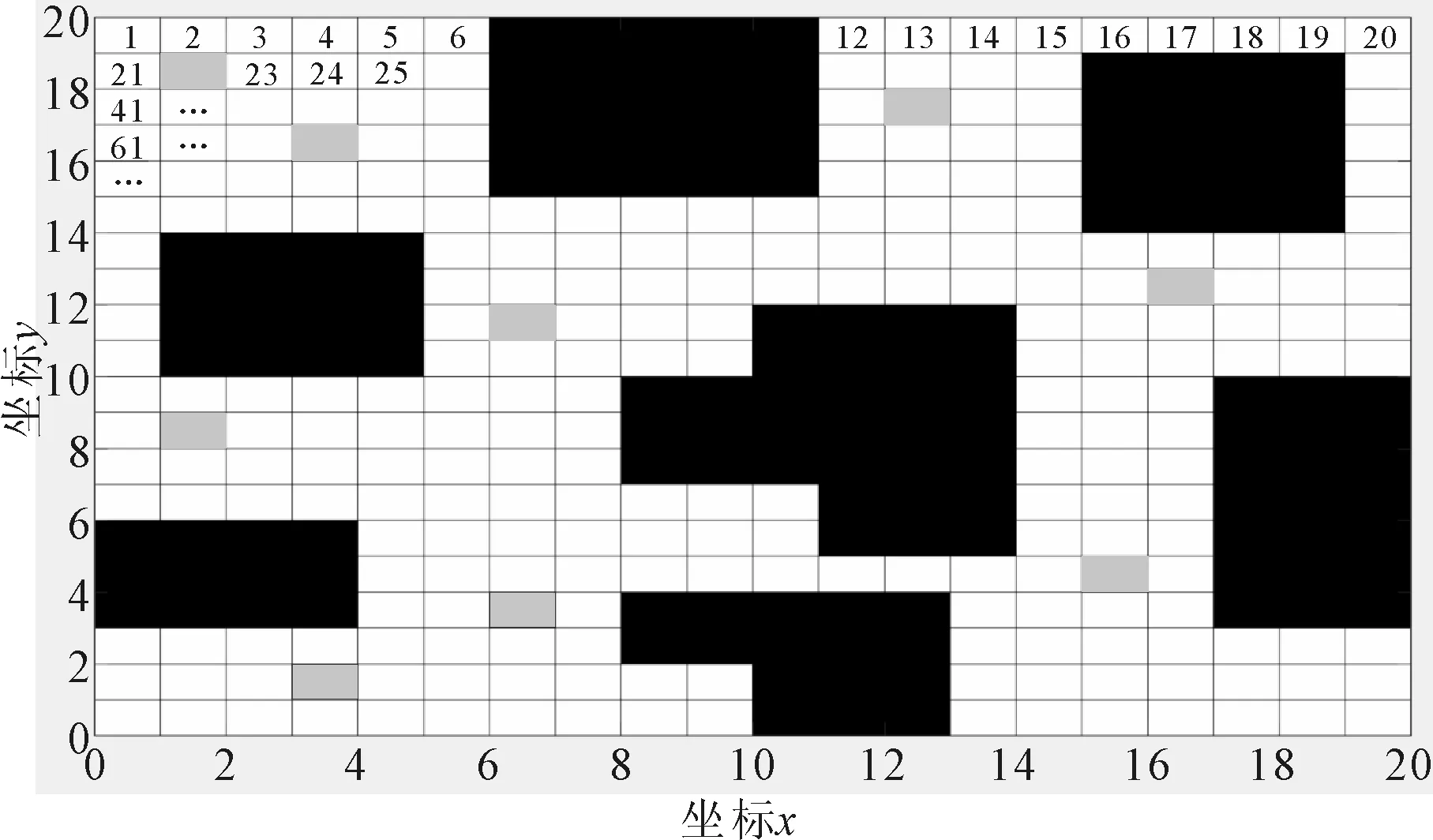
图2 工作环境栅格图

2 TSP问题

2.1 基本概念

TSP问题即在已知一个n个点的完全图，每条边都有一个长度，求总长度最短的经过所有顶点的封闭回路。其实质就是在一个带权重的完全无向图中，找到一个权值总和最小的哈密顿回路，且需满足如下的目标函数：

(2)

式中:vi为城市号，取值为1到n之间的自然数；d(vi,vj)为城市i与城市j之间的权值，对于对称式TSP问题，有d(vi,vj)=d(vj,vi)。

其数学模型可表示为：G=(V,E)为赋权完全图，V=(1,2,…,n)为顶点合集；E为边集，各顶点间的距离为Cij，即：

已知Cij>0，i,j∈V，TSP问题的数学描述为：

(3)

(4)

(5)

(6)

xij∈{0,1}

(7)

式中：dij为ij两点之间的距离。

式(3)的目标函数要求距离之和最小；式(4)表示从城市i出发；式(5)中xij=1表示走过的路线，包括城市i到城市j之间的距离，xij=0表示选择走别的路线；式(4)和式(5)确保每个城市都会经过一次，但不能保证无回头路。式(6)确保不会走回头路。

蚁群算法解决TSP问题可靠性高、适应性强、精确度高，但不能安全的进行多点路径规划。常用的解决TSP问题的步骤如图3所示。

图3 TSP步骤

对于两点之间的最短距离，用欧拉公式计算：

(8)

式中：(xi，yi),(xj,yj)分别为i点和j点的坐标。

当两点之间有障碍物时，两者之间距离发生改变，且取决于障碍物的大小、位置和个数，因此引进环境复杂度系数ζ，当ζ=1时即为普通的TSP问题。

(9)

在PCB板上焊点和障碍物是随机分布的，点与点之间的复杂度系数不一样，两点间最短路径需重新规划，因此在解决焊点避障的TSP问题时，需先解决避障问题求得各焊点之间的相互距离，再进一步解决TSP问题，完成多点间的轨迹规划。

2.2 算法流程

为了解决避障问题求得各焊点之间的相互距离，在各焊点之间采用蚁群算法，初始化参数时对焊点、障碍物的位置、大小进行标识，得到焊点的个数n，i为大于等于1小于n的正整数，j为大于等于2小于等于n的正整数，再构造解空间，在栅格环境中蚂蚁按照状态转移概率选择下一节点，最后更新信息素。当达到目标条件后，输出距离矩阵并记录路径信息，带入到TSP问题中求解。其具体步骤为：

(1)初始化参数。对工作环境的栅格图用0和1组成的矩阵来表示，0表示可行栅格，1表示不可行栅格，如图4所示。设置蚂蚁数量m，信息素启发因子α，期望启发因子β，信息素挥发因子ρ，迭代次数Nc、目标焊点栅格序号。初始化可选节点D={0,1,2,…,n-1},爬行路线和爬行路线长度。将禁忌表Bk(蚂蚁k当前走过的栅格点)初始化为空集，其中k为1，2，…,m。

图4 矩阵表示栅格图

(2)构造解空间。在已初始化的栅格图中，将蚂蚁放在初始目标焊点，其按照状态转移概率选择下一个节点，直至到达下一个目标焊点。在第t次迭代中，蚂蚁k由节点i选择下一个节点j的转移概率为：

(10)

nij=1/dij

(11)

式中:allowk为下一个时刻蚂蚁k从当前节点i到下一个所有可到达节点的集合；τij为路径(i,j)的信息素浓度；nij为启发信息；dij为当前节点和待选节点j的欧式距离;α为信息素启发因子；β为期望启发因子。

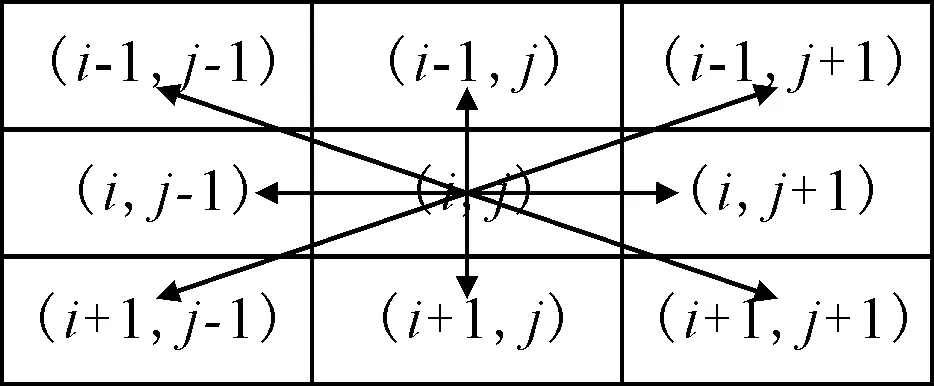
图5 移动方向

(3)更新信息素。在每一只蚂蚁选择某一节点后将会对该节点的信息素进行更新，称为实时信息素更新，更新方式为：

τij(t+1)=(1-ρ)τij(t)+ρτ0

(12)

式中：τ0为信息素初始值；ρ为区间[0,1]的信息素挥发因子。

在蚁群完成一次迭代后，所有蚂蚁到达了目标焊点，对蚁群走过路径上的信息素进行更新，其他路径上的残留信息素被挥发，这种路径信息素更新的方法为：

τij(t+1)=(1-ρ)τij(t)Δτij

(13)

(14)

(15)

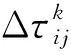
本文采用的算法执行流程如图6所示。

图6 改进蚁群算法流程

3 案例分析

笔者采用栅格法来研究焊头在二维空间上的路径规划，对图2中的所有目标焊点按从左到右、从上到下的顺序进行编号，焊点编号如图7所示。为验证蚁群算法的准确性，采用Matlab对从S5点到S6点、从S3到S4点、从S1到S7点进行路径规划仿真实验。在仿真过程中，所设置的实验参数如表1所示。考虑环境复杂度ζ的最优运动轨道和收敛曲线如图8和图9所示。

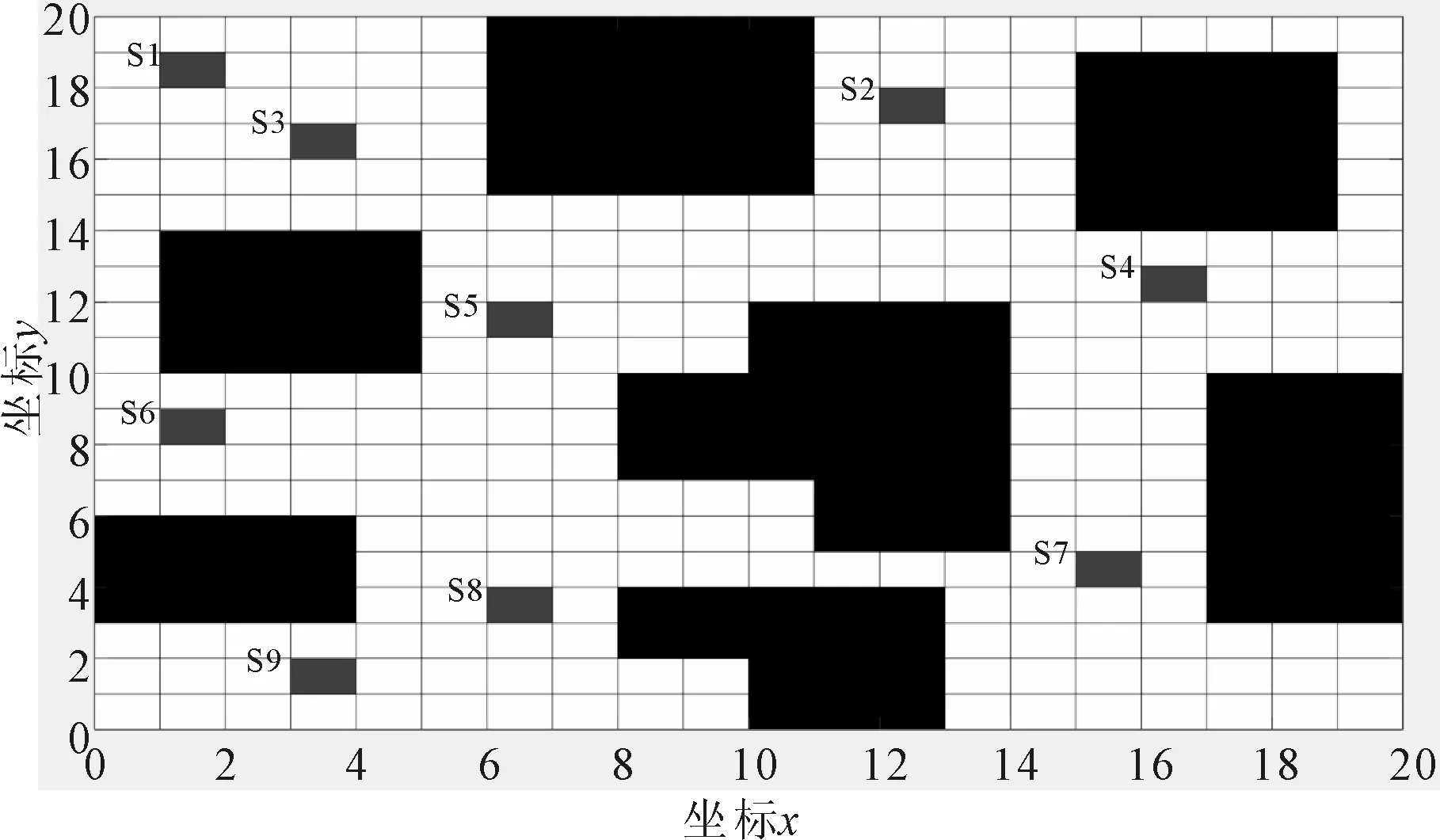
图7 焊点编号

表1 实验参数设置

从图8和图9可知，自起点出发，找到了一条避开所有障碍物的最短路径，均在最大迭代次数前达到了稳定状态。仿真实验结果如2所示，从表2可知，随着距离越长达到稳定的迭代次数增加，花费的总时间增加，且由于环境复杂度ζ的存在，迭代次数也随之增加，总时间进一步增加，稳定性越来越差。由于障碍物的大小、位置和个数的不同，造成的环境复杂度ζ不同，导致规划的轨迹最优长度难以预测，因此需要对所有焊点进行避障处理。

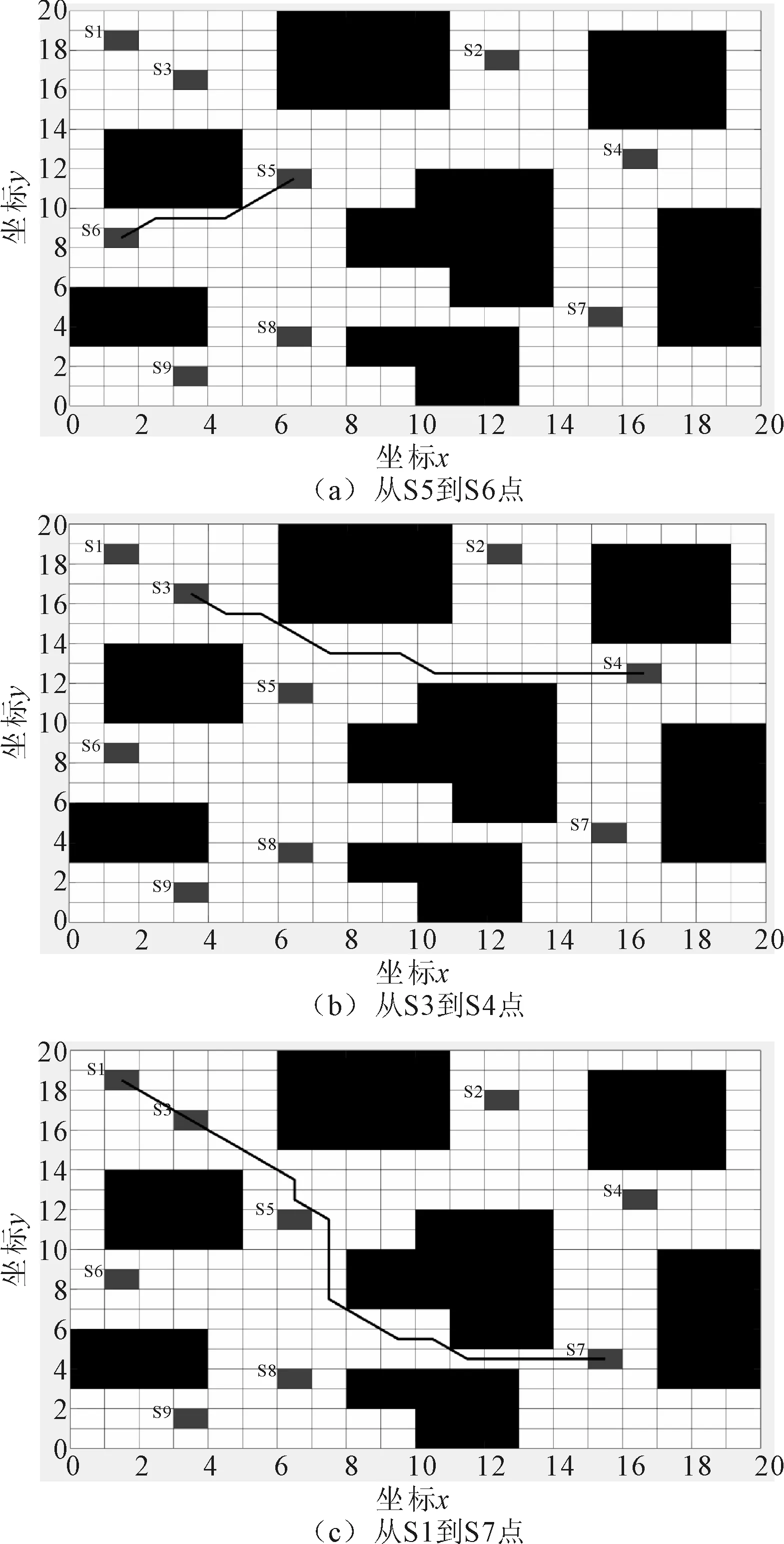
图8 考虑ζ的最优运动轨迹

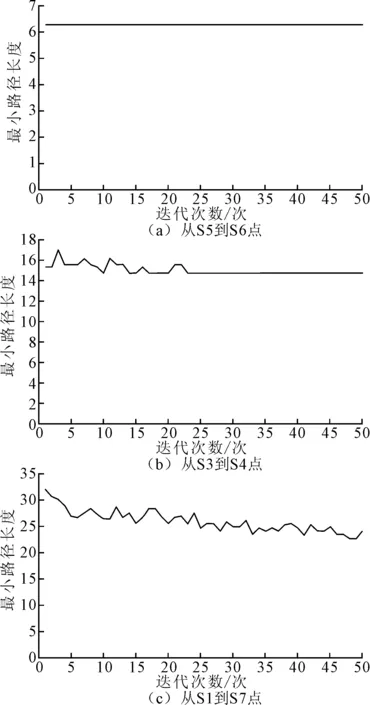
图9 考虑ζ的收敛曲线

表2 仿真实验结果

对如图7所示的所有目标焊点进行避障处理后，计算出各焊点之间的最短距离，焊点i到焊点j与焊点j到焊点i的最短距离相等，所得到的目标矩阵如图10所示，为对称矩阵。为保证分母不为0，特将对角线上的元素修正为一个非常小的正数10-4。

在经过多次迭代计算后，得到优化路径和各代的最短距离与平均距离，如图11和图12所示。根据图11和图12可知，最短路径为：S7-S4-S2-S5-S3-S1-S6-S9-S8-S7，其长度为65.941 126,在寻优过程中快速找到最短安全路径。

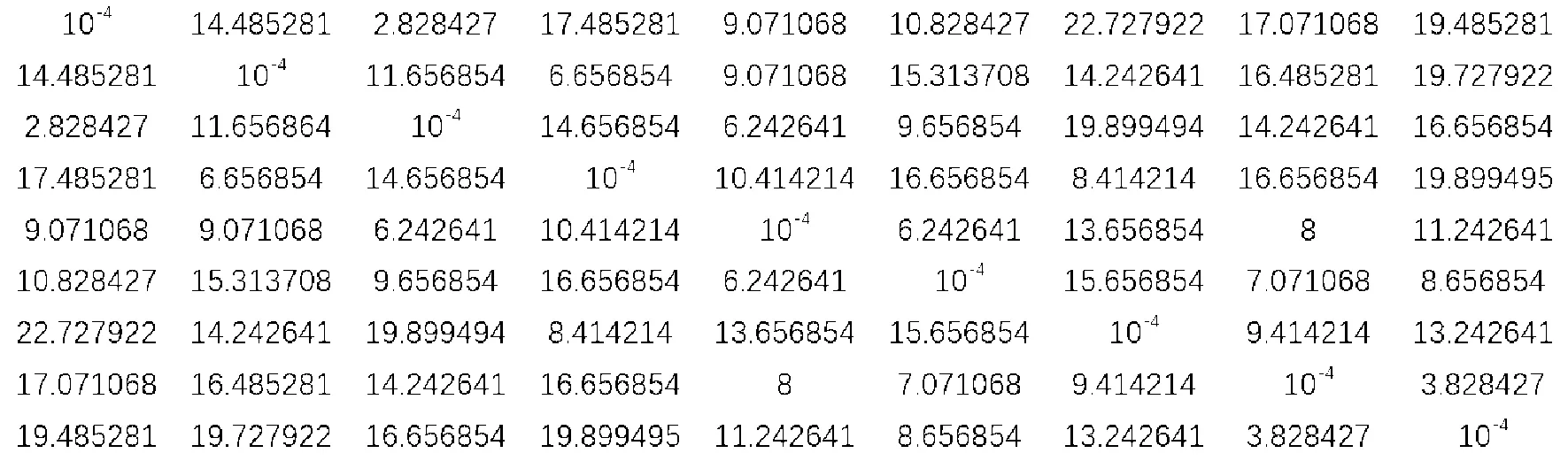
图10 距离矩阵

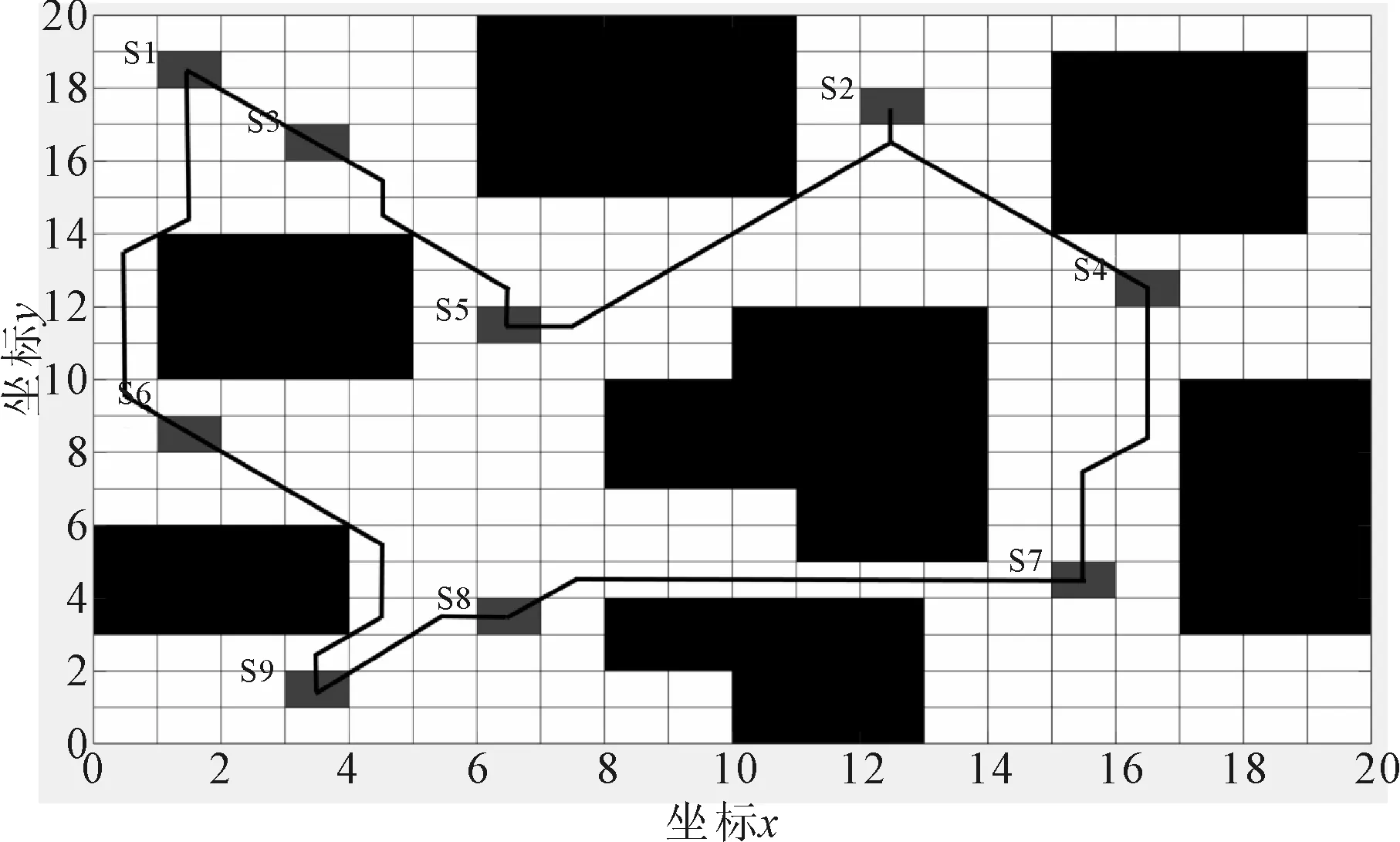
图11 蚁群算法优化路径

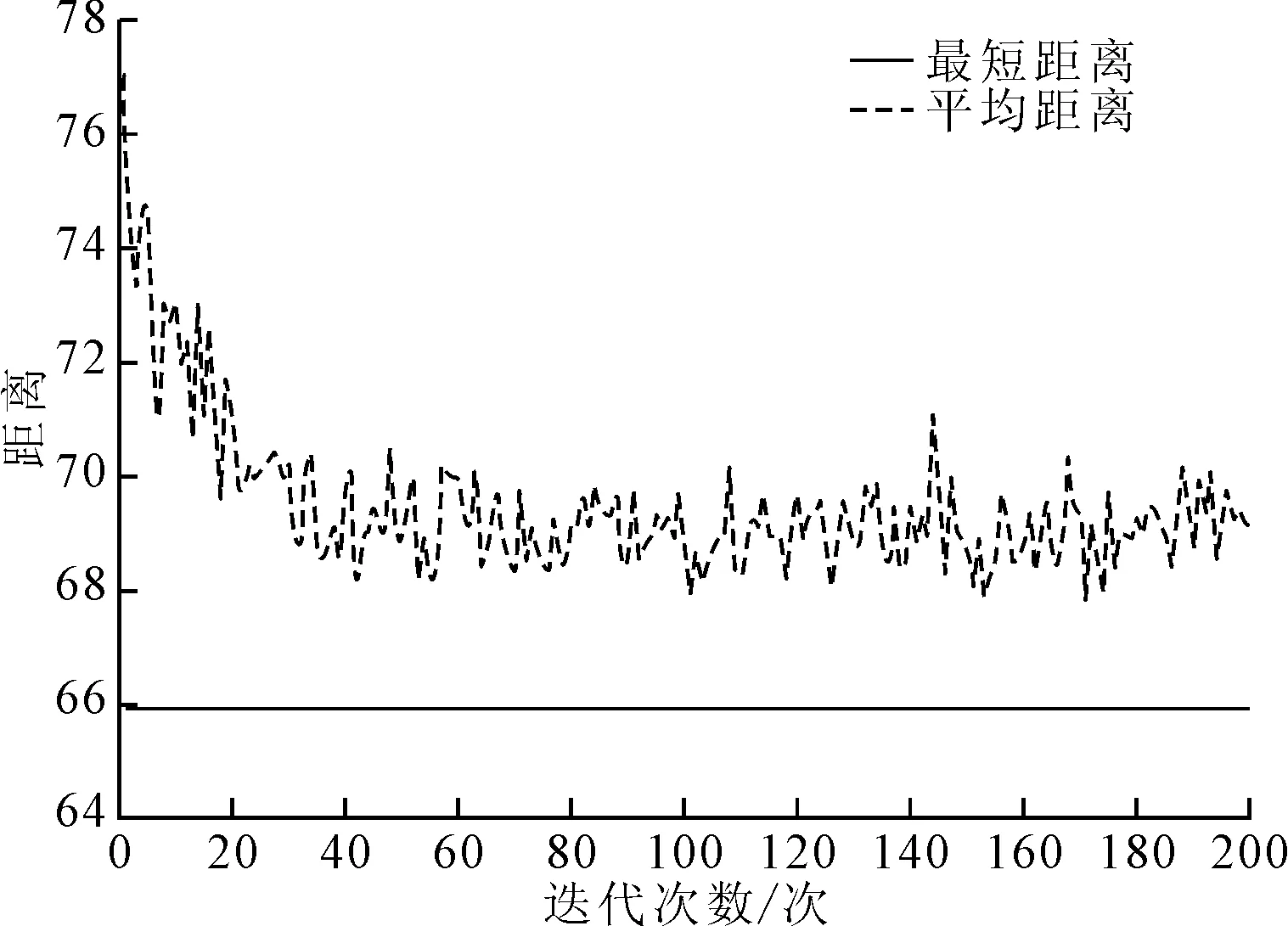
图12 各代的最短距离与平均距离对比

4 结论

针对印刷电路板上的焊点焊接问题，为了使焊头能按照某种顺序在有障碍物的有限环境中，找到一条通过多个目标焊点的最优路径，且在运动过程中能安全、无障碍的绕过所有障碍，笔者在蚁群算法解决TSP问题的基础上，提出一种精度高、安全性好的多目标多障碍路径规划的改进蚁群算法，该方法能精确地计算出点与点之间的最短安全距离，再根据点与点之间的最短安全距离得到遍历所有目标点的最短安全路径。经过仿真验证，证实了该方法的可行性和有效性，能在寻优过程中快速找到最短安全路径，克服了目前TSP问题中未考虑安全性的难题。