刚性磁悬浮转子系统碰摩动力学建模与分析
张霁阳,吴华春,胡业发,周 建,张 丽
(1.武汉理工大学 机电工程学院,湖北 武汉 430070;2.湖北省磁悬浮工程技术研究中心,湖北 武汉 430070)
磁悬浮轴承具有无接触、无需润滑、密封、转子位置精度高、可支承转速高、使用寿命长且维护费用低等特点,主要应用于高速、高精度要求的场合中,磁悬浮轴承因其特点已逐渐成为应用的主流。为防止主动磁悬浮轴承因突然断电、控制力不足或载荷突变等突发状况下,高速转子跌落后与磁悬浮轴承发生碰撞,辅助轴承仍是磁悬浮轴承系统中不可或缺的一部分[1]。但是,辅助轴承作为磁悬浮轴承系统最后的应急保护装置,在某些情况下并不能完全保证高速转子的安全,其与转子接触产生大量热量和剧烈碰撞,可能会导致辅助轴承毁坏,甚至破坏转子、磁悬浮轴承等其他部件[2]。因此,研究转子碰摩的机理,改进控制系统和优化辅助轴承,从而改善系统的控制效果并减少辅助轴承的损耗,这对提高整体系统运行的安全性和寿命具有重要意义。
Tai[3]等建立了转子系统的集中质量模型,研究了转子系统在单点碰摩下气隙和不平衡力对转子运动行为的影响。李洋[4]建立了不平衡激励下的单跨度单盘碰摩转子系统的运动微分方程,通过四阶Runge-Kutta方法进行了仿真实验。Lin[5]等研究了不同刚度、阻尼系数、转速、间隙、摩擦系数等参数对碰摩的影响。Su[6]等对磁悬浮轴承转子系统中基座受到底部冲击碰摩后的动力学行为进行了数值仿真。这些碰摩方面的研究在模型建立时,假设两端轴承相对于质心是对称的,因此,两个轴承的动态响应是相同的,实际情况中两端轴承与转子的碰摩行为会相互影响转子在两端的运动行为。Lyu[7]等提出了一种新的转子碰摩识别方法,并对不同的碰摩响应采取对应的控制算法。王东雄[8]等对磁悬浮双转子系统定点碰摩特性进行了建模分析。蒋磊[9]对磁悬浮转子失控分别跌落在固定环、滚动轴承、双层滚动轴承上的碰摩过程进行了数值仿真。Prabhat[10]等对不平衡和不对中转子系统中磁悬浮轴承和不同的辅助轴承之间的相互作用进行了研究。Keogh[11]等对由于磁性材料磁场饱和导致磁悬浮转子和辅助轴承碰摩的动力学行为进行了深入研究,为磁悬浮控制提供指导。
以上文献对磁悬浮转子系统的碰摩研究在建模时均没有考虑实际情况中电器控制元件的限制,忽略了控制器、轴承和转子之间的相互制约关系。为此,通过建立一个控制器、轴承、转子统一的系统化模型,从理论和实际两方面对磁悬浮系统中的碰摩机理进行更深入的研究,以便为磁悬浮轴承关键参数设计、控制算法设计、转子运动状态预测等提供参考。
1 磁悬浮转子碰摩的动力学建模
1.1 磁悬浮轴承及其控制器模型
磁悬浮轴承结构如图1所示,采用4对磁极,偏置45°差动励磁方式控制。为便于力的分析,文中建立的XY坐标与水平垂直方向偏置45°。
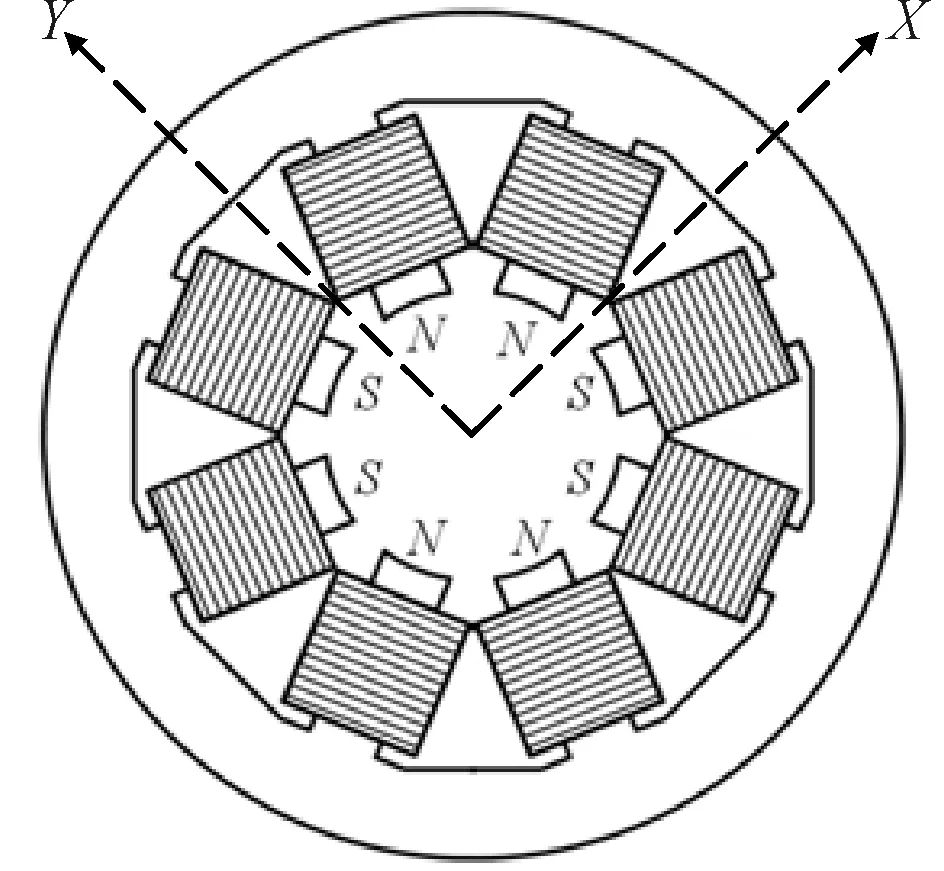
图1 磁悬浮轴承结构示意图
电磁力Fmag线性化公式经泰勒展开略去高阶项得到,Fmag=kxx+kiic,其中kx为磁悬浮轴承的力-位移刚度系数;ki为磁悬浮轴承的力-电流刚度系数;x在这里表示相对平衡位置的位移;ic为控制电流,其大小采用PID(proportional integral derivative)控制。
实际情况下,电器元件存在输出方向和有限输出的限制,建模时需要考虑这些限制。如图2所示,传感器输入位置信号保持在辅助轴承的气隙范围内,相对位置量x经过气隙范围限幅后,加上平衡位置绝对值x0得到当前位置的绝对量,经过参考电压、PID控制器运算后传递给功率放大器。其中传感器的输出电压0~5 V对应0~1 mm的输入,2.5 V即代表平衡位置,运算放大器、PID输出电压的上下限幅为±2.5 V,加上偏置电压2.5 V,这样功率放大器输入限制为0~5 V,输出为0~3 A。功率放大器输出电流减去偏置电流即可以得到控制电流ic的大小。
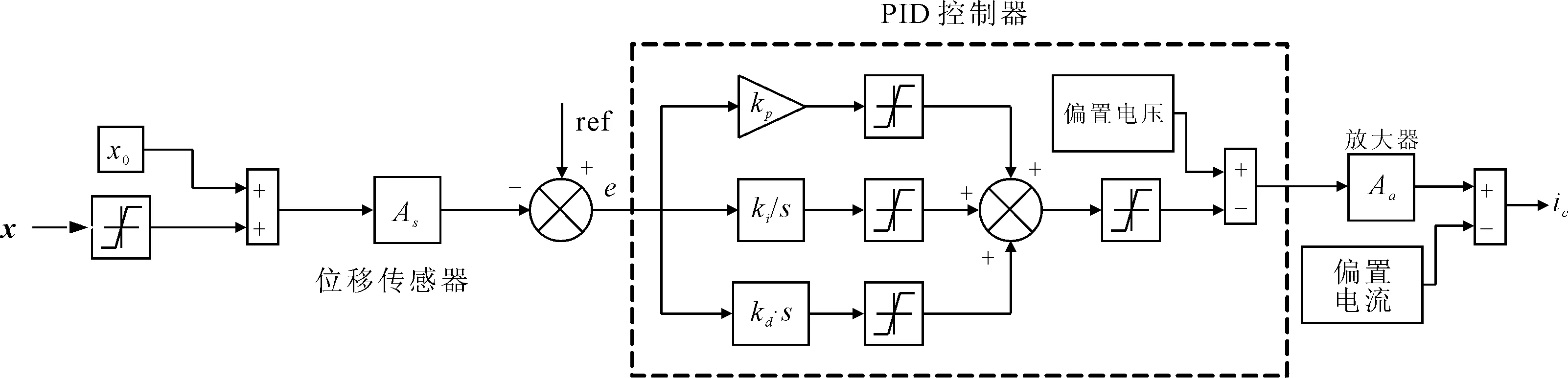
图2 控制器模型
1.2 碰摩力模型
碰摩力采用线性库仑力模型,摩擦力与正压力成正比,受力分析如图3所示。x、y为转子形心坐标位置,e为转子的偏心量,k为辅助轴承刚度,δ为转定子同轴心时的气隙大小,μ为转定子之间的滑动摩擦系数,ψ为轴承转子接触时接触点的相对速度,其法向和切向碰摩力为:
(1)
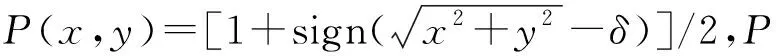
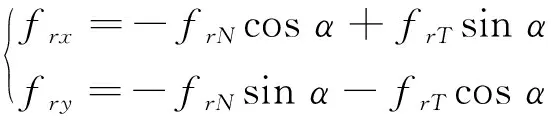
(2)
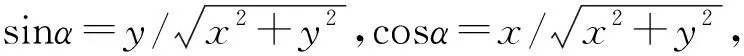
(3)
式中:rb为辅助轴承内圈半径;ω为转子角速度;x′,y′分别为x,y的导数。
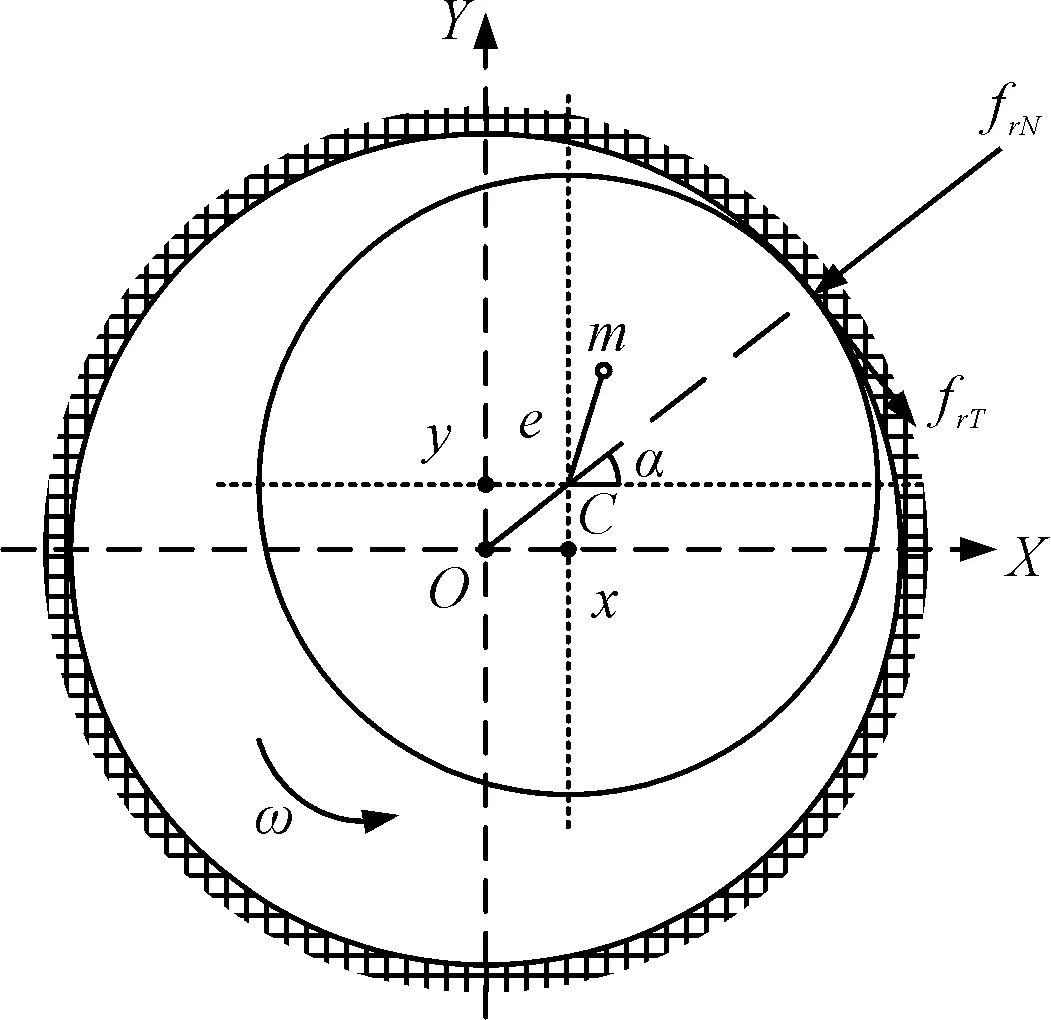
图3 转子碰摩模型
1.3 转子模型
考虑研究低速情况下的转子碰摩情况,视转子为刚性,不发生弯曲变形。由此建立刚性转子和弹性辅助轴承的系统模型,辅助轴承为机械轴承,其与转子的气隙比磁悬浮轴承更小,辅助轴承与对应的磁悬浮轴承距离较近,这里视为与之在相同位置,且辅助轴承内圈中心与平台基座一样视为固定。建立四自由度磁悬浮轴承转子系统的参考坐标系,如图4所示。以质心所在截面的形心O点建立直角坐标系Oxyz[12],Oz与转子轴线共线,la和lb分别表示两侧径向磁悬浮轴承a、b距O点的距离,ω为转子绕z轴转动角频率,θ为转子绕y轴转动角频率,φ为转子绕x轴转动角频率,角速度方向均采用逆时针绕轴为正方向。

图4 参考坐标系
根据建立的模型和基本力学公式,可推出转子的运动微分方程[13]。
(4)
式中:M为转子系统的广义质量矩阵;q为转子的广义坐标矩阵;G为转子系统的陀螺矩阵;L为转子系统的力臂系数矩阵;F为外部力矩阵;Fu为广义不平衡力矩阵。
刚性转子不考虑轴的弯曲变形,质心截面的形心,a、b端形心和x、y方向的旋转角度φ、θ均与la、lb呈比例关系[14],其中l=la+lb。
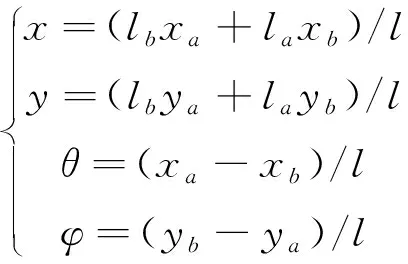
(5)
不考虑轴向作用力,结合式(4)和式(5),可转化为:
(6)
式中:xa,ya,xb,yb分别为a,b端的x,y坐标;X=[xa,xb,ya,yb]T,I=[icxa,icxb,icya,icyb]T,X为转子在各方向上的位移矩阵,I为各方向的控制电流,其中:
(7)
(8)
(9)
(10)
式(6)~式(10)中:m为转子质量;icxa为a端x方向的控制电流;kxxa为a端x方向的力-位移刚度系数;kixa为a端x方向的力-电流刚度系数,因为两端的磁悬浮轴承结构、电气参数一致,所以各位置、方向的力-位移、电流刚度系数都相等,kxxa=kxya=kxxb=kxyb=kx,kixa=kiya=kixb=kiyb=ki;Ir为转子截面惯性矩;Ia为转子极惯性矩。
1.4 磁悬浮转子系统动力学模型
Fd为外部力的合力,其中fx、fy表示x、y方向的不平衡力,frxa、frxb分别表示a端和b端轴承在x方向对转子的碰摩力;frya、fryb分别表示a端和b端轴承在y方向对转子的碰摩力。
(11)
将式(6)二阶微分方程转化为状态空间方程的形式,取
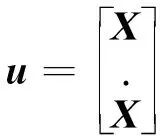
(12)
得到
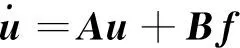
w=Cu
(13)
其中
C=[E0]
(14)
矩阵f=[I,Fd]T,包含控制电流和外部力总共8路输入,E为4行4列的单位矩阵,隐含的矩阵D为4行8列的零矩阵。
根据上述理论绘出如图5所示的转子模型框图[15],图5中共有8路输入,前4路分别为xa、xb、ya、yb方向上的控制电流,后4路为外部力Fd矩阵的每一行参数,合并后作为输入,同时也是图5中状态空间模块中的f,运算得到u,即为4路输出,分别为位移xa、xb、ya、yb,如此循环构成闭环系统模型。Simulink软件中可用mux和demux模块对多路信号进行合并与分解。
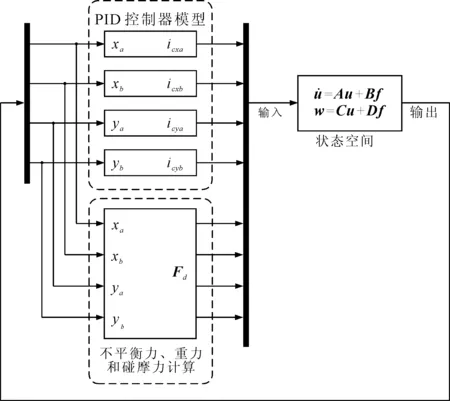
图5 四自由度转子模型框图
2 数值仿真
仿真环境采用MATLAB/Simulink R2018a版本搭建,根据图5模型框图搭建。仿真采用可变步长,采样间隔为1e-6s,运行总时间为0.8 s,设置模型参数初始值如表1所示。
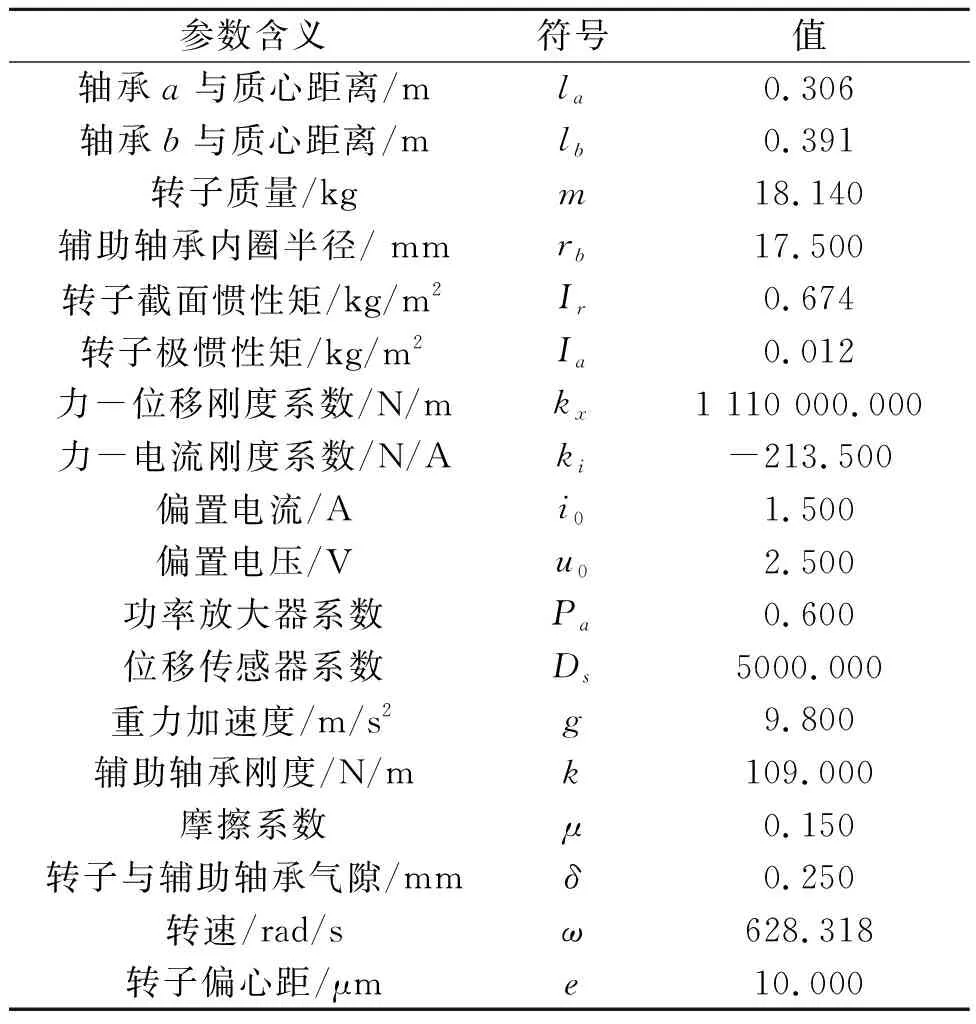
表1 碰摩Simulink模型主要初始参数
经多次试验,选取PID控制参数中的比例参数kp=2.5,积分参数ki=30,微分参数kd=0.005,使稳态误差、超调量、振荡次数符合基本要求。仿真开始时使转子从最低点静止起浮,然后开始旋转,不平衡力导致的转子轨迹运动半径约为25 μm,如图6所示。
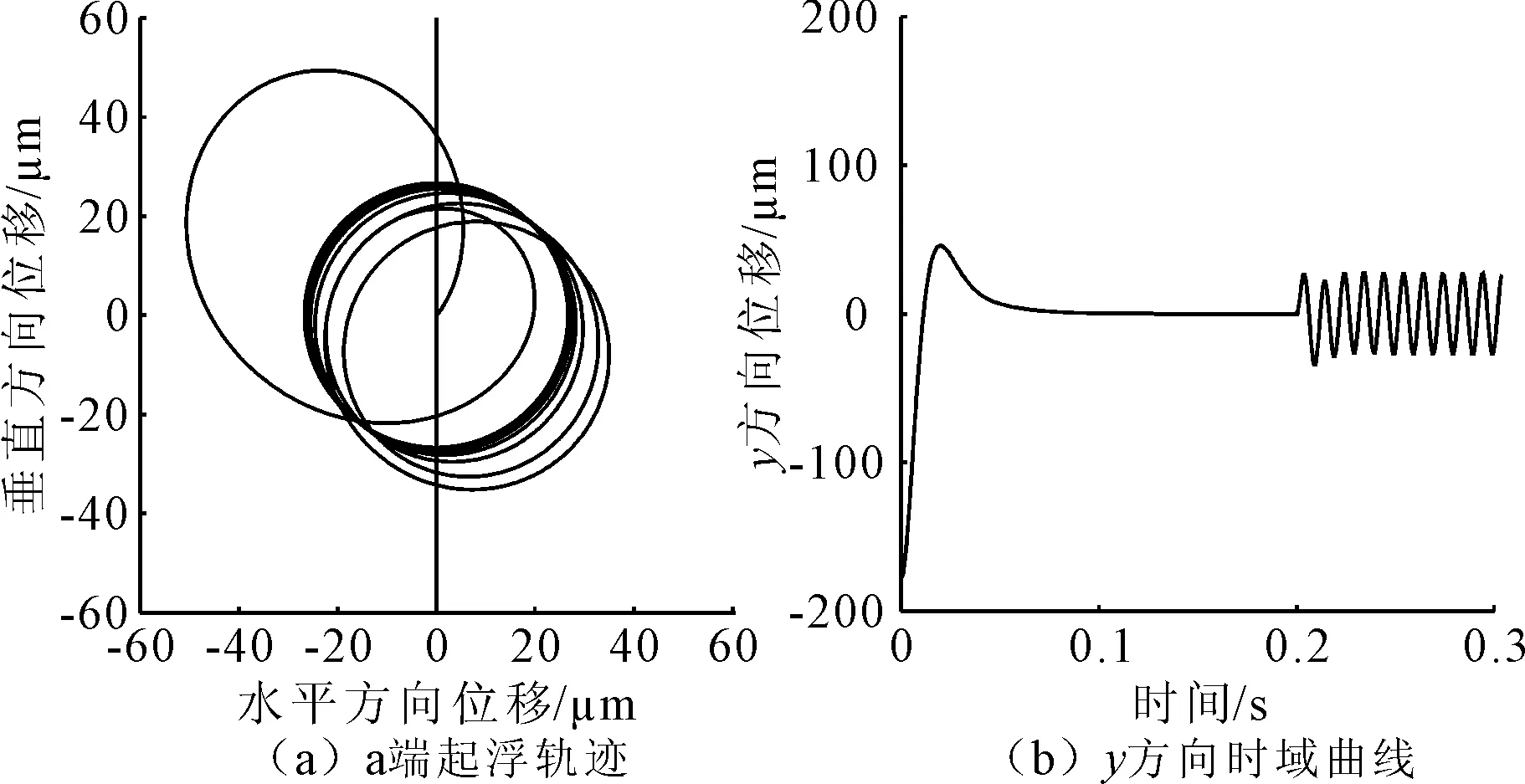
图6 转子起浮轨迹
文献[6]和文献[16]等均是采用给基座或者转子施加外力或是加速度变化来模拟其受到冲击,从而引发轴承转子碰摩。在0.2 s时刻开始旋转0.3 s后,转子处于固定半径的回转状态,在Y负方向加入一极短时间的激振力尝试模拟冲击引发碰摩现象,采用阶跃信号形式施加在质心位置,其大小F=nmg表示转子重力的n倍大小,n在仿真调节时选取,T为冲击持续时间的2倍,t为当前仿真时刻减去冲击开始时刻所经过的时间。
调节n使得转子能克服电磁力撞上辅助轴承,取n=3,冲击持续时间为0.04 s,得到如图7所示转子轨迹图,外圈的圆表示辅助轴承提供的间隙圆。
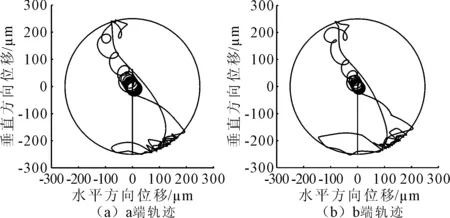
图7 转子轨迹
在冲击之前,转子以约为25 μm的运动半径旋转,在冲击后约5 ms触碰到辅助轴承,在碰撞的早期,转定子之间以较大的相互作用力碰撞,碰撞时间很短。
b端转子轨迹如图8所示,五角星表示轨迹开始位置,三角形表示轨迹结束位置,图8(a)中前4次碰撞由于受碰摩的法向和切向的作用力、不平衡力、饱和电磁力和激振力的情况下,进入了稳定的反向涡动状态,运动半径接近间隙圆半径,之后主要受激振力在持续时间内作用,转子在激振力方向左右来回小幅弹跳,运动半径迅速降低到50 μm以下。转子运动半径和碰摩力时域图如图9所示。
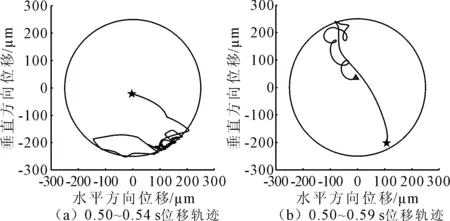
图8 b端转子轨迹
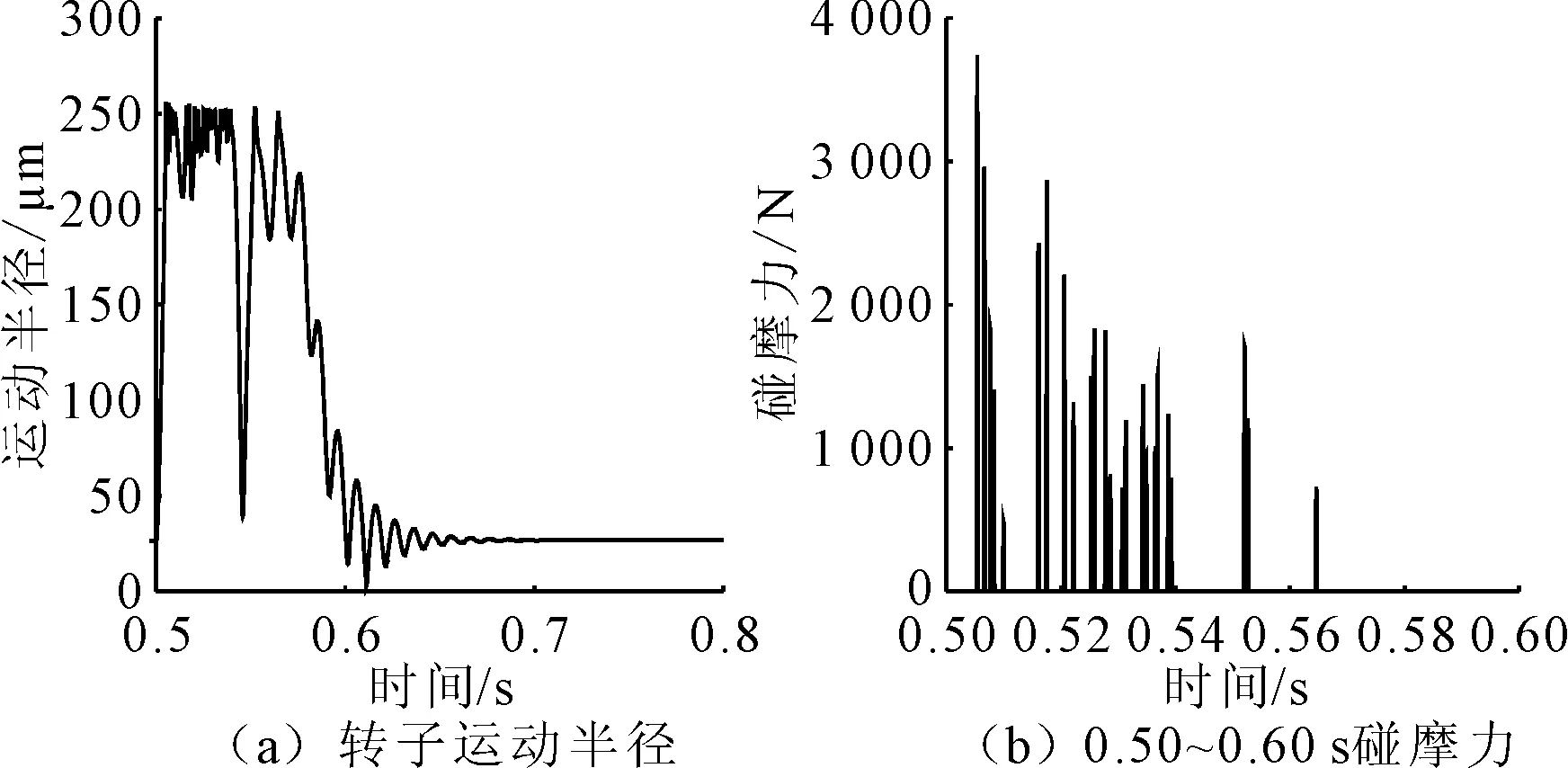
图9 转子运动半径和碰摩力时域图
从图9(b)可知,首次冲击力最大之后逐渐下降,但在合力作用下仍发生了多次碰撞,碰摩力最小值略大于nmg的大小533 N。0.54 s开始激振力作用消失,由于PID调节控制电流ic为最大,使得转子迅速回复来不及调节,转子撞击到另一边辅助轴承,如图9(a)所示,之后在电磁力作用下,逐渐回到了平衡位置。
3 结论
建立了四自由度的刚性转子和弹性辅助轴承与PID控制器、传感器、功率放大器等相结合的统一的系统模型,通过MATLAB/Simulink软件仿真模拟了在PID控制下磁悬浮轴承转子在短时间的激振力作用下转子的动力学行为。仿真结果显示首次冲击力载荷最大,并且激振力作用持续期间转子会不断地发生碰摩,当载荷消失时,电磁力控制下转子超调回稳仍会发生一些碰摩。

