一种新型可变刚度调谐质量阻尼器

罗 民，洪 流

(武汉理工大学 机电工程学院，湖北 武汉 430070)

随着科技水平的高速发展，许多机械加工的精度要求日渐提高，薄壁结构件因其具有质量轻、强度大等优点，在许多高端技术产业中有着很广泛的使用。在薄壁件的加工制造过程中，当材料切削去除比率过高时，容易产生加工振动与挠度，严重影响机械系统以及加工的精度，同时振动产生的噪音也会有害于操作人员的健康，因此控制加工中产生的振动影响显得尤为重要。

目前较为先进的零件挠度控制方法有夹具的布局设计、刀具路径优化以及切削参数的选择，其思想为提高加工件的刚度或降低加工件工作时施加的切削力[1-2]。在动态加工中的振动一般可以通过加工工艺优化和结构动力学来修正控制，Rashid等[3]根据压电致动器和自适应控制算法开发了一种主动控制系统;Yang等[4]研究了多模态薄壁零件的铣削振动衰减，设计了一种同涡流阻尼器相结合的双自由度调谐质量阻尼器；Kolluru等[5]在待加工薄壁件边缘添加了6个阻尼器，以抑制铣削过程中产生的振动，使其振动信号的均方根值得到了大幅降低。

调谐质量阻尼器的引入对系统的振动起到了有效的抑制和控制作用，且比传统的优化主体结构和加强主构件刚度等有着更高的经济适用性。被动调谐质量阻尼器的参数由需减振的主结构参数决定，在其固有激励频率下能达到最佳的减振效果，当激励不在共振频率范围，其减震效果有所减弱甚至恶化主结构的振动。相比于主动调谐质量阻尼器对硬件和软件的复杂要求，被动控制阻尼器的设计更加简单，更易于在加工中实现较好的减振效果。

笔者选用一种可变刚度机构E-Spring[6]，设计了一种新型变刚度被动调谐质量阻尼器,其可以通过旋转其两个E-Spring的角度来改变其刚度，从而抑制主体结构振动，并且通过几次振动试验验证了该设计。变刚度调谐质量阻尼器整体结构简单可靠，加工简单，实验中，变刚度调谐质量阻尼器对实验台起到明显减振效果，达到了预期的效果。

1 PTMD的动力学分析以及设计准则

1.1 动力学方程

TMD(tuned mass damper)减振系统是一种经典的二阶质量-弹簧-阻尼系统，其原理如图1所示，其动力学方程可以表示为：

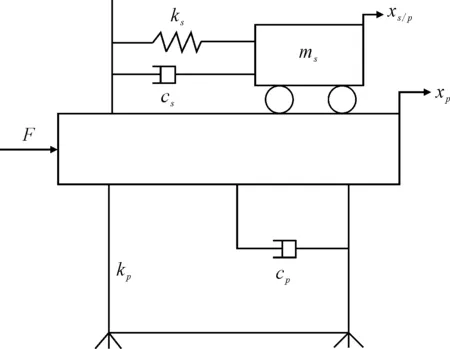
图1 TMD减振原理

kp[xp(t)-xb(t)]-ksxs/p(t)=0

(1)

(2)

式中：mp、cp、kp和ms、cs、ks分别为待减振主结构和TMD的质量、阻尼以及刚度；xp(t)为主结构振动的位移；xs/p(t)为主结构和TMD的相对位移；xb(t)为基底部的谐波激励，xb(t)=Xbsin(ωt)，ω为谐波激励频率，Xb为幅值。

令xp(t)=Xpei(ωt-φ),xs/p(t)=Xs/p(t)ei(ωt-φ)，并将式(1)和工(2)写成矩阵形式[7]：

(3)

对其求解后可以得到系统的动力响应方程：

(4)

式(4)为不计主结构阻尼的近似解析解，当引入主结构的阻尼后，系统的动力响应只能得到数值解而无法得到准确的解析解。

1.2 PTMD的设计准则

1934年，学者Den[8]在Frahm提出的由质量块和弹簧组成的TMD模型[9]上设计添加了一个粘性阻尼器，以拓宽其工作频带，被认为是最早的较为完整的TMD模型。在1998年，Rana等通过数值分析，计算出了TMD的最优参数设计公式，PTMD(pounding tuned mass damper)即是通过他们提出的最优参数公式设计出来的TMD[10]。

根据最优参数设计公式，在主结构受到基底谐波激励作用时，PTMD的最佳刚度ks和阻尼cs可以表示为：

(5)

cs=2foptξoptωpms

(6)

主体结构直接受到外部谐波激励时，最佳的频率比fopt和阻尼比ξopt可表示为：

(7)

(8)

式中：ωs和ωp分别为PTMD以及待减振主结构的固有频率；μ为TMD与主结构的质量比,μ=ms/mp,fopt=ωs/ωp。

调谐质量阻尼器在实际应用中，随着TMD质量增大，其工作的频带越宽，达到的减振效果越好，但由于TMD的质量通常会增加到主结构上，过大的质量会导致空间占用、安装难度大等不利因素，因此TMD的质量要在达到期望的减振效果的情况下尽可能的轻，一般认为当μ取值超过15%时，TMD的设计是无效的，通常情况下μ取值为5%。确定μ后将式(7)、式(8)代入式(5)、式(6)即可得到PTMD的最佳刚度和阻尼。

一般情况下，变刚度调谐质量阻尼器的固有频率和主结构的固定频率比值在0.8～1.2范围内，即：

(9)

笔者在PTMD的设计中，PTMD的固有频率和主结构固有频率比值取1，根据主结构的固有频率以及PTMD的质量，即可得到PTMD的最佳减振刚度。

2 PTMD的结构及设计

2.1 TSM及有限元仿真

笔者设计的新型PTMD中的变刚度机构TSM(tunable stiffness mechanism)采用一种异形悬臂梁结构E-Spring[8]，其结构由外圈异形悬臂梁、中心圆台以及中间的连接梁构成，其结构示意图如图2所示，尺寸参数如表1所示。在工作时，其圆心位置保持不变，E-Spring可绕其圆心旋转，对悬臂梁内壁施加沿圆心向外的力，通过旋转E-Spring角度来改变悬臂梁上的受力点位置，从而改变其弯曲、剪切和轴向参数来实现刚度的变化，达到控制刚度的效果。

图2 E-Spring结构示意图

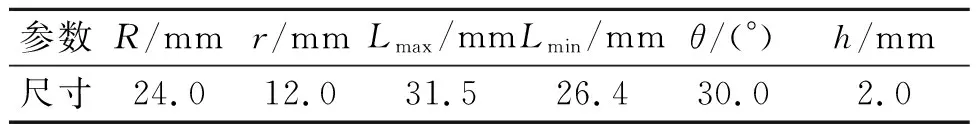
表1 E-Spring尺寸参数

E-Spring具有调节响应速度快、刚度调节范围广以及结构简单等优点，且其刚度范围可以通过壁厚、材质、异形悬臂梁的宽度等各种设计参数决定。文中E-Spring选用柔性悬臂梁设计，在厚度h不变的情况下，减小中间圆柱的半径同时增加了连接梁的宽度，以保证E-Spring的刚度以及作为TSM的实用性。

利用SolidWorks®软件绘制出E-Spring的三维模型，并将模型导入ANSYS有限元仿真软件，有限元仿真模型如图3所示。在对材料参数进行设置后，以E-Spring的圆心为原点，连接梁较长一边为Y轴建立坐标系，并每间隔22.5°在悬臂梁内侧施加一个沿E-Spring轴心向外的单位力，采集每次悬臂梁受力点的形变位移数据绘制到表格。

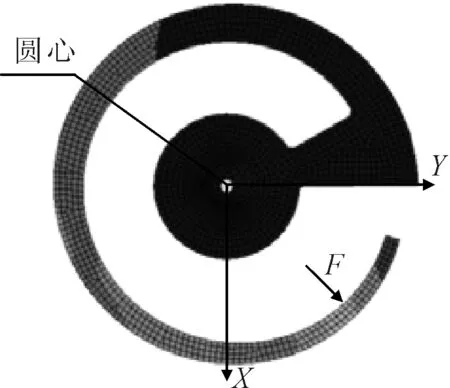
图3 有限元仿真模型

利用电子拉力计与固定基座以及限位块对E-Spring实物的实际刚度进行测试，刚度拦伸测试装置如图4所示。实验的E-Spring实物采用PLA(polylactic acid)材料3D打印加工，测试记录在不同角度下拉伸5 mm时拉力计的读数，并计算其刚度。不同角度下E-Spring仿真和实验刚度如表2和图5所示。

图4 刚度拉伸测试装置

表2 不同角度下E-Spring的仿真和实验刚度

图5 仿真与实验刚度曲线图

仿真与实验测试的角度为22.5°～180.0°，从图5可知，在22.5°～110.0°区间，仿真刚度曲线与实验曲线基本吻合，刚度由0.6 N/mm增加至1.4 N/mm左右，在110.0°～180.0°区间，实验刚度略大于仿真刚度，在180.0°时，实验刚度达到了2.36 N/mm，仿真刚度达到2.23 N/mm，分析其原因可能为3D打印材料以及实验台精度影响造成的误差，同时在刚度变大后，微小的实验误差也会被放大，最终导致仿真和实验的刚度曲线在110.0°至180.0°没有达到理想的吻合状态，实验数据和仿真数据最大偏差为5.5%，满足实验的精度要求。

2.2 PTMD的主结构设计

新型PTMD结构采用将两个E-Spring叠加的设计方式，由于E-Spring的异形悬臂并不是等宽的，而是随着旋转角度的增加而逐渐变宽，难以使用一个固定的卡扣夹住悬臂作为受力点，因此选用一个连接件将两个E-Spring的悬臂梁连接在一起，使两个E-Spring的悬臂梁形成一个夹具卡住中间的连接轴。E-Spring连接示意图如图6所示。

图6 E-Spring连接示意图

两个E-Spring分别通过3D打印的固定件固定在滑轨上，连接轴则与滑块相固定，并且连接轴上设计留有平台，方便实验中配重块的固定。在初始状态下，E-Spring悬臂梁间的空隙正好卡住连接轴保持滑块不会来回晃动，并且悬臂梁不受力保持原本的形状。

将PTMD固定在待减振结构上，随着主结构的振动，PTMD也随之振动，同时将作用力回馈施加到主结构上达到减振效果，由于PTMD中的连接件只能对E-Spring施加沿轴心向外的拉力而不能施加向内的压力，因此在工作时两个E-Spring的悬臂梁并不是同时工作而是交替受力拉伸随后回弹。PTMD整体结构示意图如图7所示。

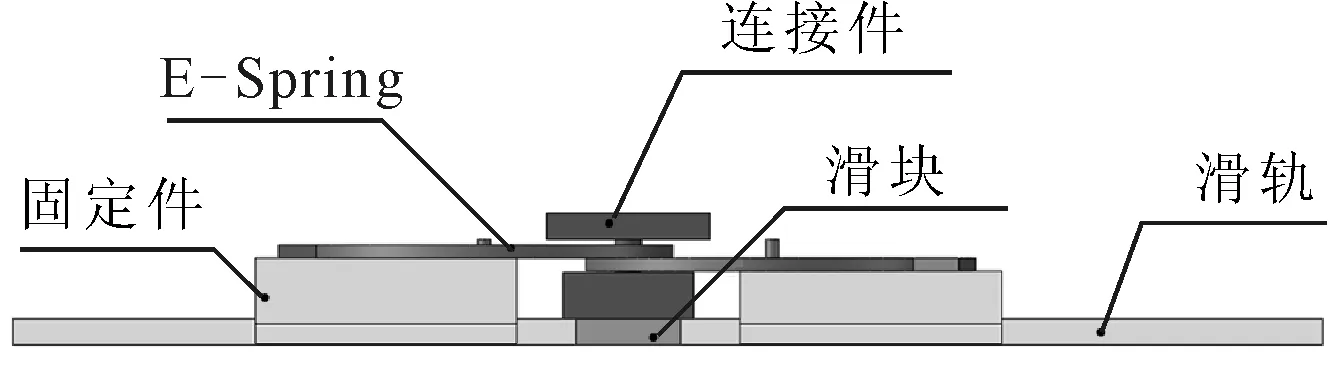
图7 PTMD整体结构示意图

3 PTMD减振实验台的设计与实验研究

3.1 减振实验台的主体结构

在振动实验中，振动实验台的主体结构一般由弹性模块和质量模块构成，质量模块可以选择钢材铝材等材料，弹性模块大致分为弹簧和悬臂梁两种。当需要垂直方向的振动时选择弹簧作为弹性模块，当需要水平方向振动时则选择矩形悬臂梁。综合考虑实验的简单性与经济性，本实验中选用的实验台为矩形悬臂梁-钢板的组合，如图8所示。4块矩形悬臂梁与上钢板和底板通过固定件和螺栓连接，在保证牢固的基础上同时方便拆卸，底板同样通过螺栓与激振器固定连接。矩形悬臂梁采用钢板加工，长240 mm，宽48 mm，厚3 mm，经计算单只悬臂梁的刚度约为4 830 N/m，减振实验台的主体结构质量测得约为10.5 kg，并且在上钢板上预留有螺栓孔位，方便后期质量调整钢块的安装与拆卸。

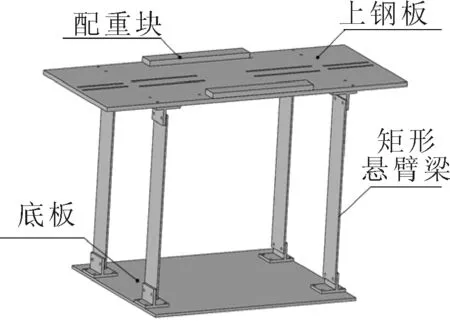
图8 实验台主结构

实验台主结构的阻尼和刚度难以直接测量，一般利用自由衰减振动的方法测量。其原理为对实验台上钢板施加一段位移或者力，让主结构做自由衰减振动，然后通过贴在主结构上的加速度传感器采集到的信号处理得到主结构的固有频率和阻尼。初步实验采用木槌敲击主结构的方式，但采集到的信号并不理想出现了很多干扰信号，随后采用对上钢板施加一段位移的方法，得到了较为顺滑的主结构自由衰减振动加速度信号。施加位移后，主结构为单自由度系统自由振动，对待减振主结构位移信号进行频谱分析得到其固有频率，主结构频谱如图9所示。从图9可知，主结构的固有频率为6.25 Hz。

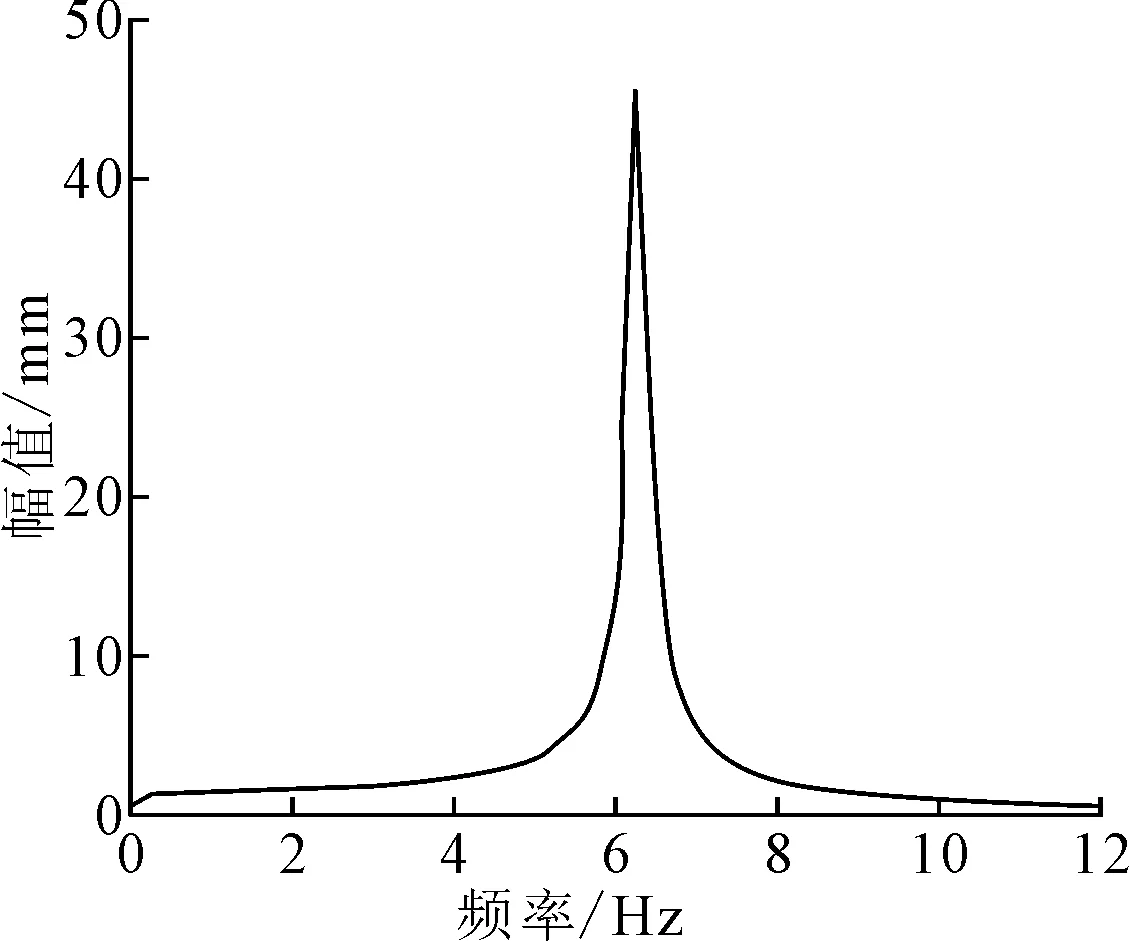
图9 主结构频谱图

实验中，质量比μ取5%，即预期PTMD质量为0.52 kg左右，经实测加上配重块后其质量为0.475 kg。将μ代入式(6)得到PTMD的阻尼为3.57 N·m/s。将主结构和PTMD的参数代入式(4),并利用Matlab绘制出主结构在安装PTMD前后幅频特性曲线，如图10所示。从图10可知，在共振频率处位移比达到42.2，在安装PTMD后主结构的位移比为4.9，降低了88.4%，在频率比0.85～1.05范围内达到减振效果，激励频率超过这个范围时，会增大主结构的振动。

图10 安装PTMD前后的幅频特性曲线

3.2 PTMD减振实验

在PTMD设计制造加工完成以及测得振动实验台主结构的固有频率后，开始研究PTMD在振动实验台上的减振效果，振动实验台如图11所示，其频率在1～100 Hz，振幅在0～5 mm内自由调节。

图11 减振实验台

由上文可知，实验主结构的固有频率为6.25 Hz，实验中将振动台的激振频率调至6.25 Hz共振频率，通过微调旋钮慢慢增大振动台的振幅，待调节至PTMD中的TSM机构也明显振动且不会过大时，停止扭动振幅微调旋钮，打开Labview软件采集加速度传感器的加速度信号，设置每秒采集1 000个信号，每次采集10 s共10 000个加速度信号。由PTMD的参数设计式(9)可知，其最佳的减振刚度ks为900 N/m ，即对应E-Spring旋转至75°左右，PTMD可以对振动实验台达到最佳的减振效果，所设计的PTMD在E-Spring旋转22.5°至180.0°区间的刚度为601～2 235 N/m，满足实验中期望最佳减振刚度。在失调情况下，即PTMD调至其他刚度时，实验台不能达到明显的减振效果，甚至可能恶化主结构的振动。本次实验测试PTMD调整至最佳刚度，即E-Spring旋转至75°(900 N/m)与PTMD失调时，即45°(750 N/m)时两个角度，采集加速度传感器的加速度信号,导入Matlab分析PTMD对振动实验台的实际减振效果。PTMD最佳刚度和失调时主结构振幅对比图如图12和图13所示。

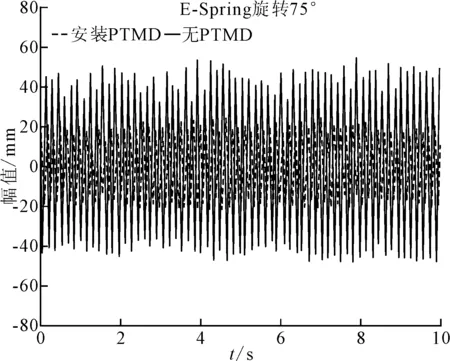
图12 PTMD最佳刚度时主结构振幅对比图

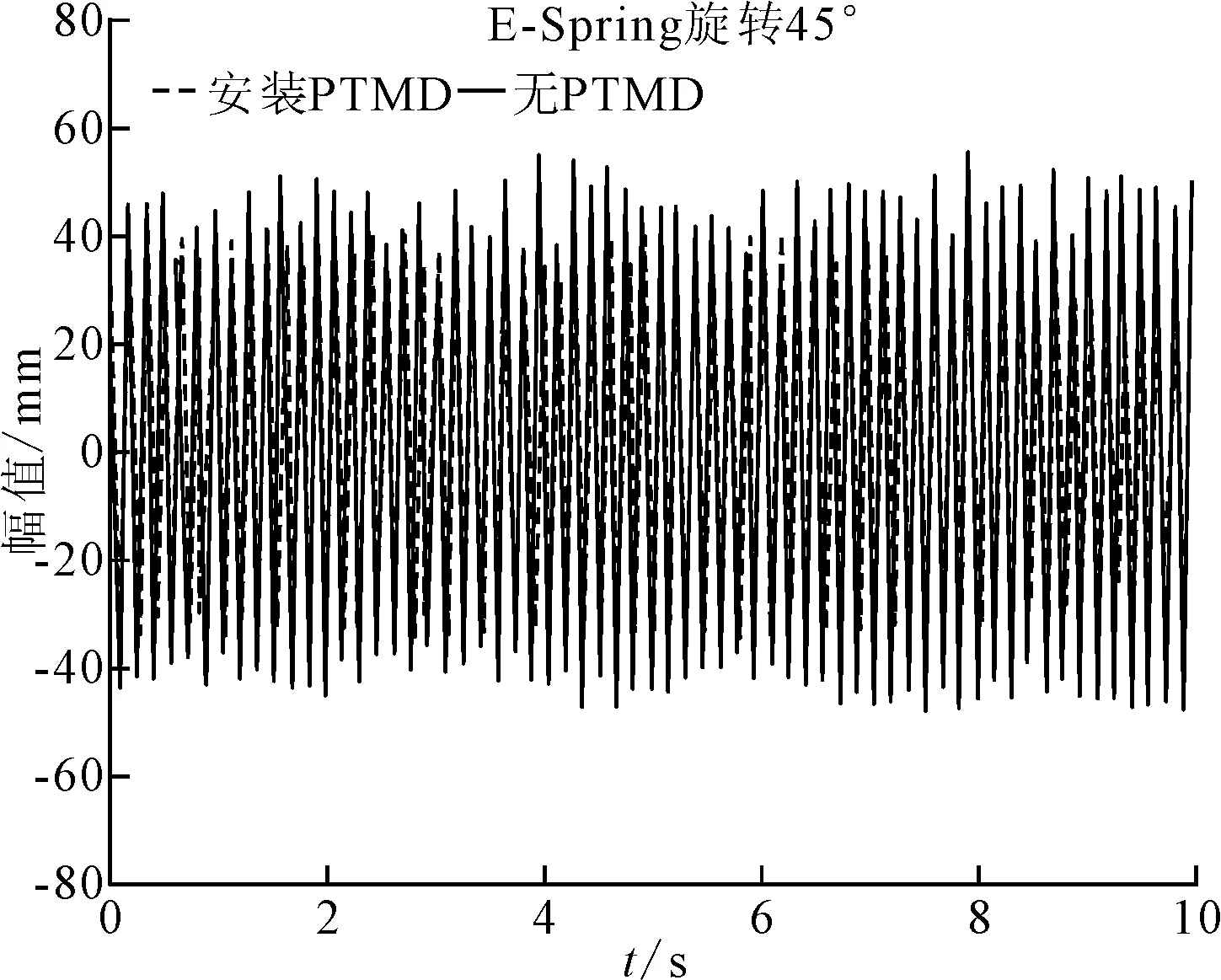
图13 PTMD失调时主结构振幅对比图

由E-Spring旋转至75°主结构振幅与未安装PTMD时主结构振幅对比分析可知，实验台的主结构振幅由24 mm降至13 mm，降低了49%，与仿真结果有一定差距，分析可能为实验误差以及实验中PTMD刚度调节误差所致，但实验PTMD也达到了对主结构较为明显的减振效果。在失调情况下，即E-Spring调至45°时，主结构的振幅变为19 mm，没有明显的减振效果，与理论推导的结果基本一致。

4 结论

针对在精密薄壁件机械加工中，材料的切削去除比率较大时容易产生加工振动的问题，影响加工精度的问题，笔者设计提出了一种变刚度被动调谐质量阻尼器，通过旋转E-Spring的角度改变PTMD的刚度，达到最佳的减振控制效果。实验表明，在实验台主结构固有频率为6.25 Hz时，将振动台调至其共振频率，PTMD在刚度调至900 N/m，实验台的振幅由24 mm明显降低至13 mm，达到了理想的实验台减振效果，同时实验测试了在失调情况下PTMD对主结构振幅的影响，结果表明在刚度未调节至最佳减振刚度时，PTMD基本没有降低主结构的振幅。所设计的变刚度调谐质量阻尼器使用于激励频率范围不大的机械加工环境，具有提升加工稳定性的效果。