串行连续生产线的可用度与缓冲库存控制研究*

林 数 吕文元

（上海理工大学管理学院 上海 200093）

1 引言

生产的连续进行是制造企业创造利润的基本条件，保持高生产率的前提是保证连续的生产，减少生产线不必要的等待时间，这对制造企业显得尤为重要［1～2］。怎样保持生产的连续进行是企业一直研究的问题，2M1B（即二个设备中间设一个缓冲库存区）的出现让企业寻求到了连续生产的保障。这种生产方式可使生产线的柔性增加，对于不可预测的因素，如设备故障等，某一设备出现故障，其设备后的缓冲库存可以继续的为下一工序提供产品，从而保证了生产的连续性，使企业的生产率大幅度提高。

串行生产线缓冲区问题一直是研究的热点问题，串行生产线是其它类型生产线的基础，对串行生产线缓冲区的研究可作为其它类型生产线缓冲区研究的基础，因此有着重要的指导意义。目前，已经有许多学者进行了研究。Enginarlar等［3］在确保生产率的基础上，提出了串行生产线最小缓冲模型。叶涛锋［4］等分析了不同类型的缓冲机制和用于确定瓶颈资源前缓冲大小的方法，建立了相应的模型，用于确定系统中瓶颈工序前的缓冲大小。郭彩芬等［5］以极大代数理论为基础，应用变分法建立生产与库存控制模型，将整个串行生产线的生产率为目标函数，得出每个中间缓冲区理想的在制品库存量应尽量接近其初始库存量。周军等［6］利用缓冲区内在制品量状态转移的概率模型，求解其状态转移概率，得出串行生产线的可用度与缓冲区容量紧密相关。谭民［7］对多级串行生产线进行了深入的研究，得到系统稳态可用度表达式，缓冲区的设置增加了系统的可用度，并且随着缓冲区容量的增加，系统可用度也增加，对系统运行是有利的。周炳海等［8］为提高串行生产线可用度和产出率，提出一种基于可用度评价的缓冲分配方法。疏松桂［9］针对带有中间缓冲库存的可修CIMS系统，基于马尔科夫过程的排队理论，解决了各设备之间生产率丢失问题。Malathrons等［10］建立了一种两机一缓冲区的可用度模型，通过马尔科夫理论求解该模型得到了该系统的可用度水平。以上研究多是从理想的串行生产线角度出发，只是考虑了缓冲区容量的优化，却没有研究缓冲区库存的补给控制。本文从实际生产线的布置结构出发，主要以串行两级子系统为主要研究对象，从系统的可用度入手，分析了缓冲区最小安全库存量，以及用非均匀节拍法对缓冲区库存进行动态的补充。

2 问题描述

理论研究中一般都是假设整条生产线每相邻的两工序之间设一缓冲区，如图1，然后在求解每个缓冲区的库存容量。这种方法比较费时费力，而且与实际的情况不相符。

图1 每两个工序间都有缓冲区的串行生产线

在实际生产线中并没有这么多的缓冲区，一般串行流水生产线减少缓冲区数量可以通过工位整合的方式来实现［11］。根据TOC理论，只是选择在生产系统的几个关键瓶颈工序前设置缓冲区，如图2，这种串行生产线结构正是本文所重点研究的。

图2 若干个相邻工序间有缓冲区的串行生产线

在文中将缓冲区及其之前的一个工序和之后的瓶颈工序三部分组成的部分称为生产线的“两级串行生产线”（图中虚线框所示）。本文以整条串行生产线上有限的这样几个“两级串行生产线”为研究对象，对每个两级串行生产线进行单独分析，从而大大简化了问题的复杂性。以保证生产线的可用度为目标，对缓冲区的容量进行简单近似的设计，建立缓冲区最小安全库存量模型以及库存补给模型，来解决串行流水生产线因瓶颈工序降低生产线生产率的问题。

3 两级串联生产线模型

3.1 两级生产线可用度模型

对于每个两级串行生产线是串行生产线的基础，研究两级串行生产线对于整个生产线有着重要的意义。两级串行生产线如图3所示，M2是生产线的瓶颈设备，在其前面设置缓冲区，保证生产的连续性。

图3 两级串行生产线

对两级串行生产线的求解思路为，首先对生产线的正常工作状态进行分类，计算出每类状态的概率，然后计算出每一类中保证生产线能够正常工作的缓冲区所处的状态概率，最后计算出两级生产线的可用度。如图3所示，设 Mi（i=1，2）为可修设备，其失效率、修复率、生产率分别为 λi、μi、wi，并且均服从指数分布，B为缓冲区，其容量为K。

根据生产线的实际生产情况，同时为了分析问题的需要，作出如下假设：

1）设备发生故障时可通过及时修理使其恢复如新。

2）缓冲区绝对可靠，不会发生故障。

3）两个设备不会同时发生故障。

4）前一设备不饥饿，后一设备不堵塞。

5）从缓冲区中存取工件的时间忽略不计。

6）随机变量之间相互独立。

对于图3所示的两级串行生产线，可以将其所有状态总结为以下几种情况：

1）状态1：M1和M2均正常工作。

2）状态2：M1故障，M2正常工作。

3）状态3：M1正常工作，M2故障。

其状态转移图如图4所示。

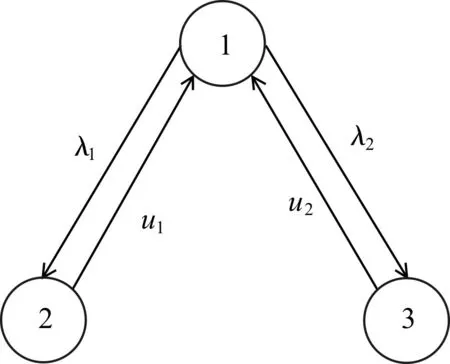
图4 两级串行生产线状态转移图

根据图4可得两级串行生产线的状态转移概率方程为

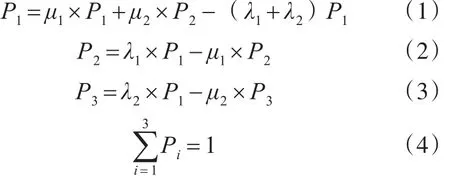
当生产线稳态运行时，另P2=0，P3=0，由式（1）～（4）解稳态方程得：

所以，两级串行生产线位于状态1的概率为P1=1（1+ λ1μ1+ λ2μ2），位于状态 2的概 率 为P2=（λ1μ1）P1，位 于 状 态 3 的 概 率 为 P3=（λ2μ2）P1。

下面讨论缓冲区的情况，两级生产线正常工作的状态包括：

1）处于状态1时，M1和M2都正常工作且M2不空闲。

2）处于状态2时，M1故障，M2正常工作且缓冲区不空。

3）处于状态3时，M1正常工作，M2故障且缓冲区不满。

首先看状态1，此时要使两级生产线正常工作，必须保证M2不空闲。在两级生产线稳态时，其生产率为w=min(w1，w2)，所以M2不空闲的概率为

在状态2时，缓冲区的容量为K，所以要在此状态下正常工作，只要使缓冲区不空即可，此时缓冲区的状态转移图如图5所示。

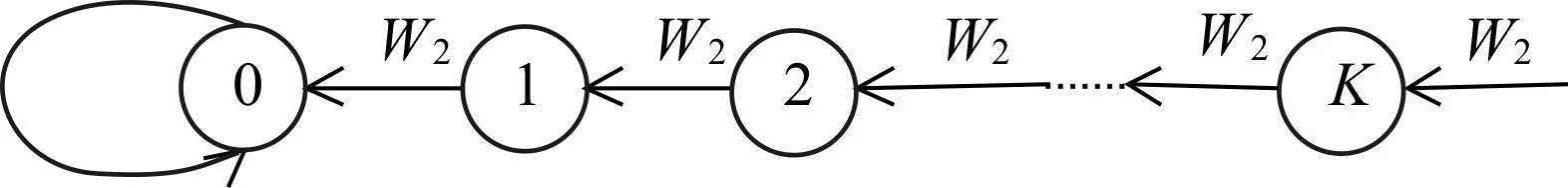
图5 缓冲区状态转移图

由图5可得在状态2下的缓冲区状态转移方程：

在两级串行生产线稳态情况下，依次令，PiB=0（i=0，1，2，…，k-1），得到：

所以在状态2时，缓冲区不空的概率为

在状态3情况下，要在此状态下正常工作，必须使缓冲区不满，此时缓冲区的状态转移图如图6所示。

由图6可得在状态3下的缓冲区状态转移方程：

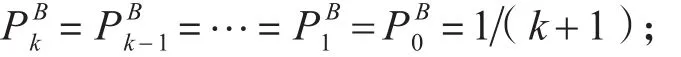
所以在状态3时，缓冲区不满的概率为

由式（5）～（10）可以得出两级串行生产线的稳态可用度为

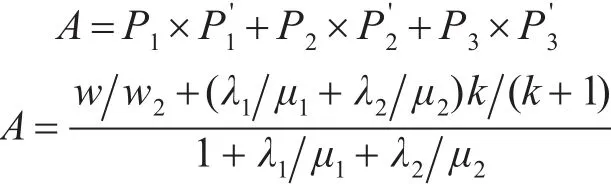
这就是两级串行生产线的可用度，从上式可以看出，两级生产线可用度A是缓冲区容量K的函数，可用度的大小与设备的故障率、修复率、生产率、缓冲区容量相关，只要确定可用度A以后，就可以很快求出缓冲区的容量。由于我们假设缓冲区设置在瓶颈工序前面，所以w=min(w1，w2)=w2，所以有

在上式中，我们在对K进行讨论，有

这就是不带缓冲区的刚性两级生产线的可用度。

图6 缓冲区状态转移图

这就是带有无限缓冲区的理想两级生产线的可用度。

通过上述方法，在对整条串行生产线的若干个两级串行生产线进行逐个分析，就可以分别求出每个缓冲区的容量。

3.2 缓冲区最小安全库存量模型

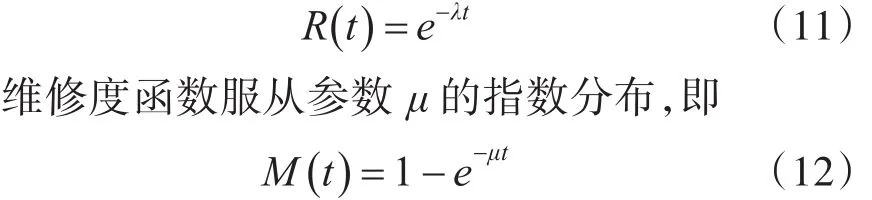
由两级生产线可用度模型得出了其稳态可用度，可知系统处于平稳状态时，其所处的状态与开始状态无关，我们假设设备均处于偶然故障期，故障分布服从指数分布，λi、μi分别为设备Mi的故障率与修复率。对于两级生产线子系统，系统的可靠度［12～13］R（t）为在两级串行生产线系统中，若要求得缓冲区最小安全库存量，则两级串行生产线需处于状态2的情况下。即M1故障，M2正常工作，此时当M1故障时，瓶颈设备M2消耗缓冲区的库存，当缓冲区库存量消耗尽时，两级串行生产线系统才会失效。在生产周期T（T＞MTTR）内，设备M1平均修复时间为

在建立缓冲区最小安全库存量模型前，假设：

1）缓冲区在生产周期内完全可靠，工件在缓冲区运输时间忽略不计。

2）工序M1不饥饿，瓶颈工序M2不堵塞。

3）r1为M1的生产节拍，r2为瓶颈工序M2的生产节拍，r1＜r2，BS为缓冲区的库存量。

4）设备发生故障时可通过及时修理使其恢复如新。

当工序M1发生故障时，必须要求工序M1的平均修复时间小于缓冲区的缓冲时间，即

将式（13）带入上式得，两级串行生产线系统能连续生产的条件为

式中0.5为设备M1故障时，其下级设备M2正在加工产品数的均值。由式（15）可得，两级串行生产线要保持连续生产，则缓冲区最小安全库存量为

由式（16）可知，两级串行生产线的最小安全库存量的大小与设备的修复率、瓶颈设备的生产节拍、生产周期相关。

3.3 缓冲库存补给模型

缓冲区库存的补给一般通过设备的额外工作时间来实现，但这种方法容易影响生产节奏，并且不易规范生产等。在研究两级串行生产线的基础上，提出了非均匀节拍控制的方法［14］，可有效地避免这些问题。假设某两级串行连续生产线如图7所示。其中第m台设备为瓶颈设备，ri为各设备的生产节拍，因为生产线的生产节拍取决于瓶颈设备，所以rm=r0。

图7 两级串行连续生产线

假设设备均处于偶然故障期，故障率属于CFR型，λi、μi分别为设备Mi的故障率与修复率。则由可靠性理论［15］可知，设备Mi的可靠度服从指数分布：

由图7所示，以瓶颈设备Mm与前级设备Mm-1为研究对象，设备Mm-1的故障模型如图8所示。

图8 设备Mm-1的n次故障模型

设Bm-1Si为Bm-1第i（i=1，2，3…，n）次发生故障时的库存量，则：

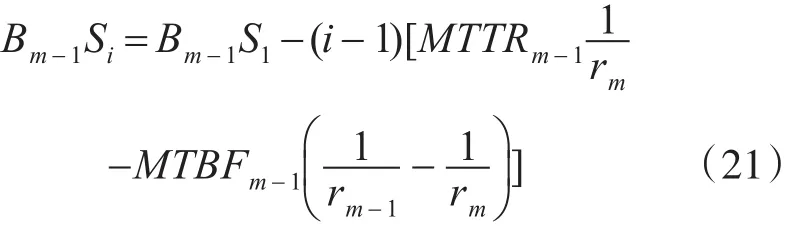
要满足Bm-1Si=Bm-1S1，即缓冲区初始的库存量等于设备Mm-1第i次故障时缓冲区的库存量，必须使：

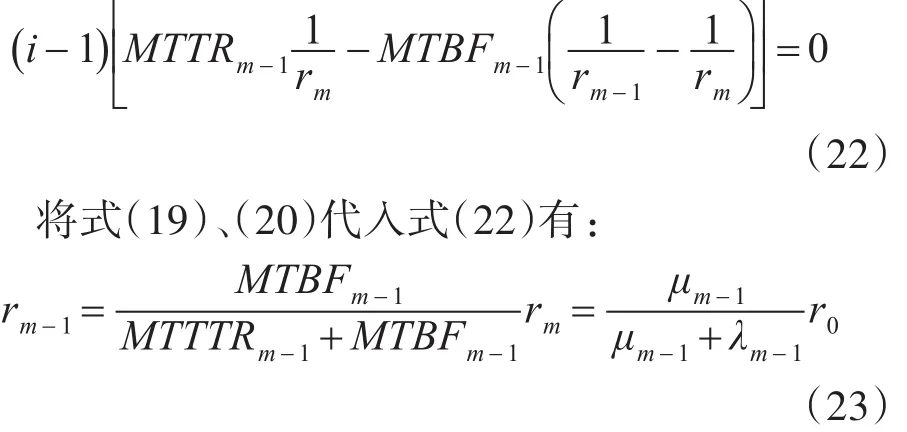
由式（23）、3.2可知，在两级串行生产线系统中，当瓶颈前级设备发生故障时，此时瓶颈设备消耗缓冲区库存来保证生产的连续性，当瓶颈前级设备恢复正常，此时缓冲区内库存量以不能维持下一次缓冲生产，所以应该调节瓶颈前级设备的生产节拍，来补给缓冲区的库存，3.2节以给出缓冲区最小安全库存量，由式（23）得出瓶颈前级设备与瓶颈设备的节拍关系式，可根据两者来平衡缓冲区内的库存量，使生产线保持生产的连续性。

4 结语

1）基于可靠性理论中的可修复系统模型为基础，建立了两级串行生产线模型。根据马尔科夫状态转移过程得到了两级串行生产线可用度的计算公式。得出两级串行生产线的可用度与设备的失效率、修复率、缓冲区容量相关。2）通过建立两级串行生产线缓冲区最小安全库存量模型，为保证生产的连续性，得到了缓冲区库存的最小安全库存量的计算公式。3）在建立最小安全库存量库存补给模型时，提出了非均匀生产节拍的方法，通过控制节拍来保障缓冲库存，避免了串行生产线因补给缓冲库存增加额外生产时间，具有一定的应用价值。4）本文是基于两级串行具有瓶颈生产线的研究，串行生产线是一种简单的结构，是研究并联、混联等复杂生产系统的基础，基于多级具有瓶颈生产线的结构，还有待进一步研究。