基于优化克隆选择算法的云资源调度研究*

杨 丽朱 博

（1.湖北大学计算机与信息工程学院 武汉 430062）（2.武汉数字工程研究所 武汉 420205）

1 引言

资源调度问题分为两大类：以性能为目标的调度和以经济为目标的调度，以性能为目标的资源调度算法将许多影响调度性能的因素忽略掉（例如，网络流量、资源当前负载、资源价格等），只考虑资源的处理速度和任务的长度这两个关键因素。它们以最小化整体执行时间来匹配任务与资源的映射，任务分配和资源调度问题是NP难的组合优化问题［1］。而基于经济学的调度方法将资源成本作为优化的条件准则，其优化调度依赖于资源使用成本和用户需求规格的折中［2］，其将任务的执行时间考虑为固定不变和确定性的。

在实际的云环境中，资源价格是用户必要考虑的因素之一，是影响任务运行性能的一个关键因素。而网络流量和资源负载都是动态变化的，它们影响着任务的执行速度，所以任务的执行速度也是动态变化的。因此，云环境中资源调度也是一个模糊调度问题［3］。在云环境下，要确实获取可用资源的处理速度以及用户应用任务的处理时间等信息是一项困难的工作。通常，获得可用资源的速度信息还比较容易，但要获取用户任务的计算处理时间就相当复杂。因此，在运行调度任务时，需要从用户的应用规格说明或历史数据中动态地、近似地估计任务长度。

本文受De Castro和Von Zuben所提出的克隆选择算法的启发［4］，在其基础之上进行优化和扩展，提出了具有模糊处理时间的人工免疫调度算法，将其应用在云环境的资源调度中，验证了其有效性和高效性。

2 克隆选择算法的优化

2.1 克隆选择原理

在人工免疫系统（Artificial Immune System，AIS）中，自适应免疫应答过程中的关键问题之一是在免疫应答过程中如何生成大量能够识别抗原的抗体。Burnet［5］于 1959 年提出了克隆选择学说，其原理是，生物免疫系统中，由骨髓分泌的B细胞是唯一能够产生抗体的免疫细胞，当抗原进入生物体后，免疫应答被激发，B细胞群体中那些能够产生与抗原紧密结合的细胞将获得增殖、分化，这些新的B细胞将加入体液循环中，而那些与抗原之间无法结合的B细胞将会死亡，从而逐步退出体液循环。

2.2 基于克隆选择原理的优化算法

克隆选择主要的特征是免疫细胞在抗原刺激下产生克隆增殖，随后通过遗传变异分化为多样性的效应细胞（如抗体细胞）和记忆细胞。克隆选择对应着亲和度成熟（affinity maturation）的过程。即对抗原亲和度较低的个体在克隆选择机制的作用下，经历增殖复制和变异操作后，其亲和度逐步提高而“成熟”的过程。因此亲和度成熟本身是一个选择和变异的过程，即进化的过程［6～7］。在克隆选择模型中采用了交叉、变异等遗传算子，并采用相应的群体控制机制来控制种群的规模。优化算法主要流程如下：

步骤1：随机产生候选方案集S（P），该集合为记忆细胞子集（M）和剩余群体（Pr）的总和（P=Pr+M）；

步骤2：基于亲和度度量确定群体P中的n个最佳个体Pn；

步骤3：对群体中的这n个最佳个体进行克隆（复制），生成临时克隆群体C；克隆规模是抗原亲和度度量的单调增函数；

步骤4：对克隆生成的群体施加变异操作，变异概率反比于抗体的亲和度，从而生成一个成熟的抗体群体（C*）；

步骤5：从C*中重新选择改进的个体组成记忆集合，P集合的一些成员可以由C*的其他改进成员加以替换；

步骤6：替换群体中的d个低亲和度的抗体，从而维持抗体的多样性。

该算法与传统的遗传算法类似，只是在计算过程中通过抗体的散布性计算避免某种抗体具有过高的浓度，在计算过程中不仅要考虑抗体的适应度，同时考虑抗体的浓度，当抗体浓度过高或者过低其选则的可能性都将减低，即避免GA算法过早地收敛到一种方案，确保计算过程中解的多样性。此外通过免疫记忆机制，该算法可以保存各个局部最优解。

2.3 算法比较实验

将本文提出的克隆优化模型与遗传算法（GA）求 解 函 数 f(x ，y)=x⋅sin(4 πx)-y⋅cos(4 πy-π )+1在{(x，y)|-1≤x≤1，-1≤y≤1}范围上的最大值为例，比较说明两算法之间的差异。遗传算法采用标准的优胜劣汰法，每一代种群的规模为100，迭代次数为25，变异概率为0.1，交叉概率为0.3。克隆优化算法种群的规模，迭代次数分别为100和25，变异概率为0.3，最大克隆数量为10。

图1和图2分别是基于标准的遗传算法和克隆优化算法的计算结果。图1是GA算法结束后种群的分布情况，从该图可清晰地看到大多数的个体集中在一个峰值上，只有少量的个体在另一个峰值及其他局部最优解上；而图2所示的抗体种群则广泛分布在该范围内的各个峰值上，而且存在一些分布在局部最优解上的个体。这意味着克隆优化算法更适应于求解多个最优解的情况。

图1 GA运算结果的种群分布

图2 克隆选择优化算法运算结果的种群分布

3 云环境下的资源调度研究与仿真

3.1 资源调度建模

这里假定所研究的云环境中资源的调度是基于市场经济条件的。用户创建和发起包含应用规格说明和服务质量需求（具有优化策略的时间和预算约束）的应用。将云计算环境作如下的形式化描述：需要调度的任务总数为n，资源总数为p。其中，J=｛j1，j2，…，jn｝表示 n 个独立的用户任务，M=｛m1，m2，…，mp｝代表 p个计算资源的集合，～tij表示任务i（=1，2，…，n）在资源j（=1，2，…，p）上的运行时间。是三角型模糊数，其成员函数μ如图3所示。

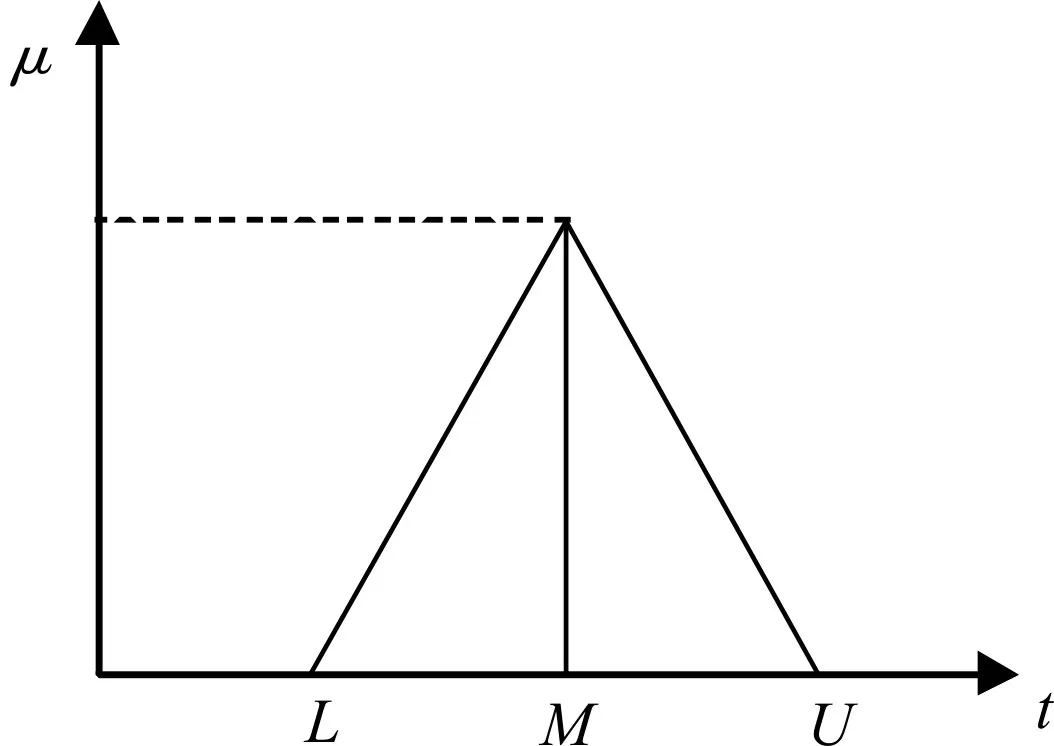
图3 三角型成员函数

这里，任务处理时间可以用下面的成员函数进行表示：

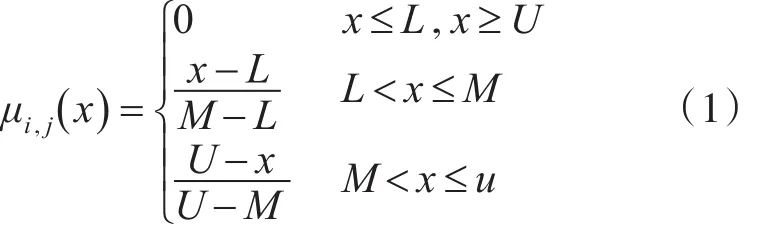
任务的一种调度策略可以用n×p的0-1矩阵X表示，其中，p为资源总数，n为任务总数，矩阵元素xi，j表示任务ji分配到资源mj上进行运行。当且仅当任务 ji被分配给计算资源 mj时，xi，j=1；否则，xi，j=0。矩阵的任意一行必有一个元素为1，也只能有一个元素为1。

假定X代表所有可能的调度方案集π中的一种调度策略，则在该调度策略下，系统完成全部任务J所需的执行时间C由下式给定：

云环境的每个资源的运行价格是由资源的所有者所决定的，其单位时间的运行价格由Bj表示（j=1，2，…，p）。运行一个应用的总的预算由B表示。

因此，云环境中资源调度问题，就是以下式为目标函数的最优化问题：

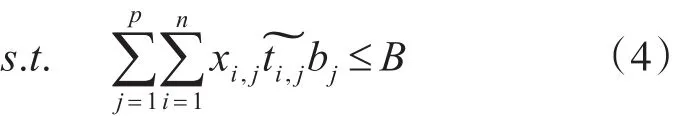
为了求解该最优化问题，在本文中，采用模糊目标满意度评估函数进行求解。

对某个调度策略来说，如果应用的完成时间低于Tmin，则它就是一个好的调度方案。这是一个模糊目标，其模糊成员函数μG如图4所示。其中，Tmin表示用最快的资源并行处理所有的任务所需的时间；Tmax表示用最慢的资源串行处理所有的任务所需的时间。

图4 模糊目标和模糊完成时间之间的重叠区

由于每个任务的处理时间是三角型模糊数，从模糊集理论可知，C（X）也必然为三角型模糊数，其成员函数μC如图4所示。

模糊目标和模糊处理时间的重叠面积SGC如式（5）所示：

如果μG和μC之间的重叠区域越大，则SGC越大。因而，模糊目标满意度fA可以用SGC对SC的比率表示：

模糊目标满意度可以作为本文的调度决策评估函数。市场条件下的模糊任务调度问题就是在预算约束的条件下最大化其调度决策评估函数。即

3.2 具有模糊处理时间的资源免疫调度算法

求解式（1）中所提出的优化问题，方法一般分为两类：获得最优解，或获得次优解（速度较快）。前者包括完全搜索、分支限界算法、回溯法等［8］；而后者包括模拟退火、塔布搜索［9～10］以及遗传算法等［11～13］。

本文提出了一种资源免疫调度算法（Resource Immune Scheduling Algorithms，RISA）来求解云计算环境的资源分配问题［14］。算法思想主要遵循两个免疫原理：克隆选择（Clonal Selection，CS）和亲和度成熟（Affinity Maturation，AM）。并作如下规定：每个资源的运行速度用单位时间执行的指令数（MIPS）表示，资源的运行价格用每单位时间元表示，应用任务的大小用指令条数（百万）表示。任何任务ji在资源mj上的运行不能中断暂停。具体算法如下：

随机生成大小为K的抗体种群P；

For每一代种群do

｛

（1）计算每个抗体的亲和度；

（2）根据亲和度选定N个最佳抗体，构成子种群PN（在选择最佳抗体时，必须满足预算约束条件）；∕*N为算法的参数*∕

（3）For each抗体in PNdo

｛

根据每个抗体的亲和度克隆复制抗体，放入临时种群C中；∕*每个抗体的克隆数量和该抗体亲和度成正比*∕

｝

（4）For each抗体in C do

｛

对种群C的每个抗体进行超变异，形成种群C*；∕*变异概率与亲和度成反比*∕

｝

（5）从种群C*中选择亲和度得到改进的抗体，形成免疫记忆细胞群M；∕*注意预算约束条件的满足*∕

（6）将原种群P中亲和度最低的|M|+D个抗体用免疫记忆细胞群M和随机产生的D个抗体进行替换而构成下一代新的种群P；∕*引入随机产生的抗体，是为了避免陷入局部最优，其中，D也是算法的参数。*∕

｝

Until算法满足停止条件；

从种群中选择具有最佳亲和度的抗体作为算法的解。

这里，算法停止条件可以采用遗传算法的停止条件，我们采用50代后停止运行，其中具有最佳亲和度的抗体即为调度的解。

4 实验与仿真

本文使用Cloudsim云环境调度模拟器［15～16］，与Min-min算法、Max-min算法的性能进行比较。Min-min算法，首先计算每个未分配任务对所有机器的最小完成时间，然后，具有全局最小完成时间的任务被选择出来，分配给相应的机器。最后，重复执行上面的过程。Max-min算法类似于Min-min算法，但它选择具有整体最大完成时间的任务分配给相应的机器。

通过Cloudsim提供的随机生成的主机处理能力，以及网络带宽和通信延迟，可以描述实际的云计算环境；通过随机生成的数据传输量和计算量，并设置依赖关系，可以描述前面定义的任务模式。测试在一台奔腾Ⅳ的主机上完成，每个测试均取三次模拟结果的平均值，并以Cloudsim中的虚拟时间单位计量。图5是元任务中包含不同任务数量，调度到50个计算资源的模拟结果。

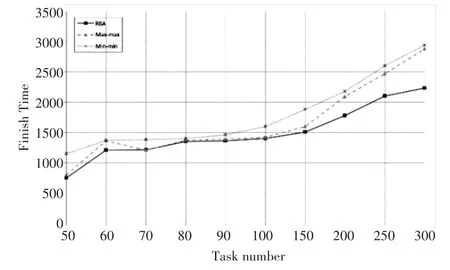
图5 任务∕时间关系

图6 资源∕时间关系

图6 是固定元任务中的任务数量为100，变化计算资源数量的模拟结果。从图中可以看出Min算法和Max算法的性能近似，且曲线平滑，但Max性能稍好，这是因为随机生成的任务不平均，该算法先调度执行时间长的任务，避免了短任务完成后，个别长任务占据资源引起其他资源空闲的情况。

5 结语

本文对云环境中的资源调度问题进行了研究，提出了RISA算法。RISA算法考虑了资源调度问题中存在的影响任务运行速度的因素，将任务的运行时间作为模糊时间，算法的核心思想是用免疫算法求解任务分配问题，通过对免疫算法中克隆选择算法的优化，将其应用于求解资源分配问题，并通过仿真实验，验证了算法的有效性和高效性。