管内过冷流动沸腾CFD模型参数敏感性研究

尚泽敏，杨立新,*，袁小菲，刘 伟，刘 余，蒋汀岚

(1.北京交通大学 机械与电子控制工程学院，北京 100044； 2.中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610213)

采用流动换热模式是冷却高功率密度反应堆燃料元件的有效方法。与单相强制对流相比，过冷流动沸腾能大幅提高换热效率，在高热流密度的场景中得到越来越多的应用。研究过冷流动沸腾的流动特性和传热特性对反应堆的运行安全及经济性具有重要意义。

随着计算机硬件的飞速发展和商业软件的不断进步，利用计算流体力学(CFD)方法模拟流动沸腾现象引起了越来越多的关注。流动沸腾的数值模拟需要多种模型相互耦合，Judd等[1]在实验观察和理论分析的基础上，提出了一种反映池沸腾过程的机理模型，将壁面总热流分为液相对流传热、蒸发和淬冷热流3部分。随后，Kurul等[2]将该模型编译成CFD代码来模拟垂直管道内的过冷沸腾。目前流动沸腾数值计算方法大多基于Kurul等给出的壁面沸腾模型，又称为PRI模型。秦浩等[3]基于OpenFOAM平台对管内流动沸腾现象进行了数值模拟，验证了模型的有效性。Filho等[4]基于FLUENT对欧拉双流体模型中气液界面换热系数及气泡脱离频率进行了研究。李权等[5]基于欧拉双流体模型对非均匀加热圆管的临界热流密度(CHF)及临界位置进行了预测。郑乐乐等[6]使用STAR-CCM+基于欧拉双流体模型对管内核态沸腾进行了数值模拟，并对DNB型临界热流密度进行了预测。上述研究已成功模拟了多种条件下的流动沸腾现象，CFD方法可靠性得到越来越多的验证，同时其中相关模型也得到了诸多改进。但目前针对欧拉双流体模型框架内众多的辅助模型进行参数敏感性分析的研究较少，且对各种相间作用力的计算与否尚无统一认识。

因此，本研究基于商用CFD分析软件STAR-CCM+，采用欧拉双流体模型结合 RPI 模型对管内过冷流动沸腾进行数值模拟。基于实验结果对两相计算中网格模型、湍流模型、沸腾子模型及相间作用力模型的参数进行敏感性分析。

1 模型描述

1.1 控制方程

欧拉双流体模型将两相流场中各相均视作连续介质且充满整个流场，各相流动变量在交界面上发生间断并产生质量、动量和能量传递现象。由于流动沸腾过程中气泡与液相之间存在较强的相互作用力，如曳力和非曳力等，因此更适合采用两流体模型描述。

体积守恒方程(流场中气体与液相体积分数(αl、αg)之和为1)：

αl+αg=1

(1)

连续性方程：

(2)

动量方程：

(3)

能量方程：

(4)

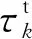
1.2 相间质量、能量及动量传递

气液相间的质量传递速率取决于从液体侧和蒸汽侧到相间饱和界面的传热。假设两相间的能量传递均通过交界面进行，则有：

Qlg=hlga(Tsat-Tl)

(5)

Qgl=hgla(Tsat-Tg)

(6)

式中：Qlg和Qgl分别为气液界面与液相和气相间的传热；a为相界面面积密度；hlg和hgl分别为气液界面与液相和气相间的换热系数，通常用下式计算：

hlg=Nulλl/db

(7)

hgl=Nugλg/db

(8)

其中：λl和λg分别为液相和气相的热导率；db为气泡直径。对于液相，Nul通常根据Ranz-Marshall关系式[7]计算。

(9)

而气相的努塞尔数Nug一般给定为常数。

(10)

式中，hfg为汽化潜热。

如上所述，流动沸腾过程中气泡与液相之间存在较强的相互作用力Mk，习惯上将其分为曳力FD和非曳力，其中非曳力包括升力FL、湍流耗散力FTD、壁面润滑力FWL、虚拟质量力FVM，则有：

Mk=FD+FTD+FL+FWL+FVM

(11)

这5种相间作用力的计算公式及常用模型列于表1，并简单描述了各作用力对气泡的影响。

1.3 壁面沸腾模型

流体流动过程中受到加热，壁面总热量qwall可分为液相对流传热ql、蒸发传热qq、气液置换(淬冷)传热qe和气相对流传热qg4部分。壁面沸腾模型公式如下：

qwall=(ql+qq+qe)(1-Kdry)+Kdryqg

(12)

式中，Kdry为蒸汽壁面接触面积分数，采用下式计算：

(13)

(14)

其中：αδ为近壁面网格单元的平均空泡份额；αdry为临界空泡份额，默认值为0.9。4部分热量计算公式可参考文献[13]。其中，淬冷传热量qe计算公式中的Kquench为气泡影响壁面面积分数，可根据Kurul等[2]提出的模型计算：

(15)

式中，FA为在汽化核心密度和气泡影响面积分数间进行比例缩放的系数。

蒸发热流量计算公式中的Dd、Nw和f分别为气泡脱离直径、汽化核心密度和气泡脱离频率。这些参数需要额外的辅助模型才能完成对方程的封闭，辅助模型来源于实验或由理论推导总结出的经验关系式。众多汽化核心密度模型中，形式较为简单的Lemmert-Chawla模型[14]得到广泛应用。该模型认为汽化核心密度是壁面过热度ΔTsup的函数，其在两相计算中的鲁棒性较好，容易获得初始解。然而，此模型基于低压实验数据整理而来，实际上压力对汽化核心密度有显著影响，一般压力越高，气泡尺寸越小，更难脱离加热面，从而使得汽化核心密度增大。为解决Lemmert-Chawla模型在高压工况下适应性不足这一问题，在Hibiki-Ishii汽化核心密度模型的基础上，Li等[15]基于公开获取的实验数据，开发了新的汽化核心密度模型，此模型考虑了压力、壁面过热度及壁面接触角的影响。本研究使用的辅助模型列于表2。

表1 相间相互作用力模型Table 1 Model of interfacial momentum transfer

2 计算工况及几何建模

Bartolomei等[20]对垂直上升管内的过冷流动沸腾进行了实验研究，对不同管径、热流密度、进口质量流速、进口过冷度及压力下的轴向空泡份额及温度分布进行了测量。本文选用压力4.5 MPa、热流密度570 kW/m2、进口质量流速900 kg/(m2·s)、进口过冷度60 K的工况进行数值模型研究。实验中加热段长2 m、管道直径15.4 mm。

为减小进口段效应的影响，几何建模时在进口与加热段之间留出200 mm的流动发展空间(大于10倍当量直径)。在加热段与出口之间设置100 mm长的绝热段以保持数值计算的稳定性。采用二维轴对称边界条件，使用结构化网格对流体域进行划分。建模的几何结构如图1所示。

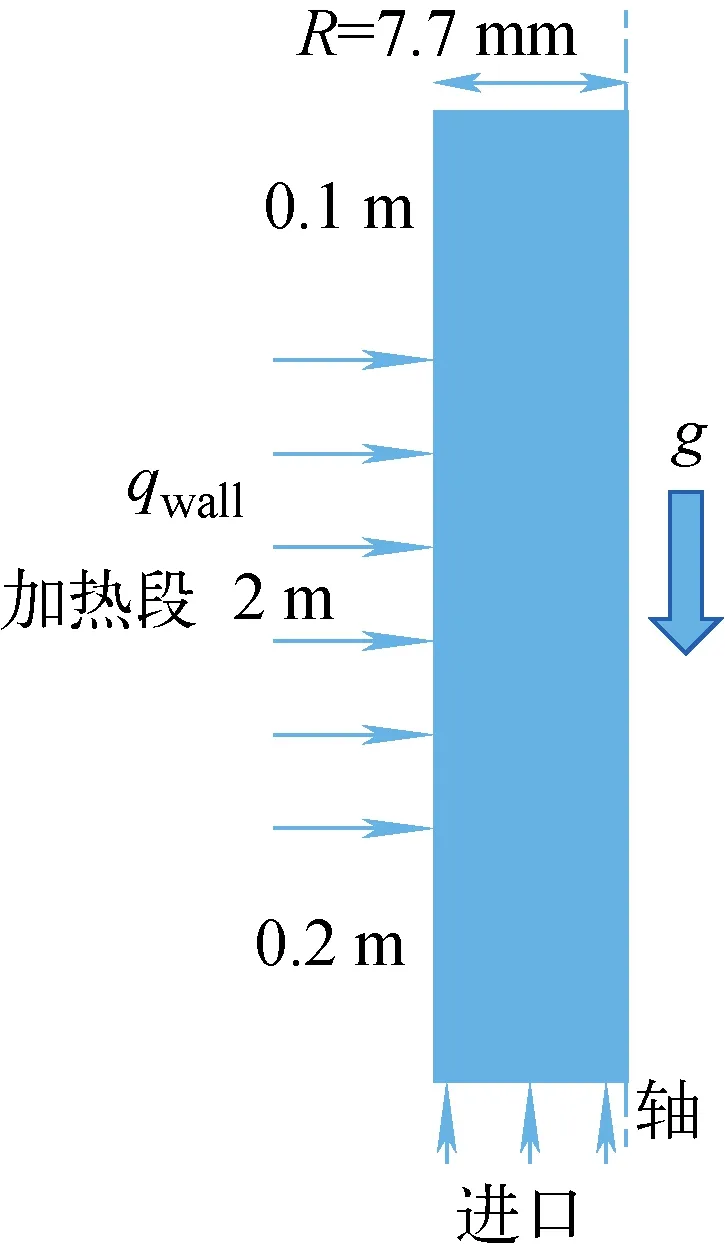
图1 实验段几何结构示意图Fig.1 Geometry of experimental section

3 模型敏感性分析

3.1 网格及湍流模型的敏感性分析

为研究网格对计算结果的影响，本文从径向和轴向两个维度进行分析。设置不同的径向分割数使加热面处第1层网格高度从0.003 mm到0.4 mm变化。当前工况下，对应壁面y+范围为1～150，网格参数设置列于表3。随后，在径向20层均匀分割的条件下，设置不同的轴向拉伸层数(85、115、145及175)生成另外4组网格。

选取标准k-ω模型、SSTk-ω模型、标准k-ε模型、Realizablek-ε模型及Realizablek-ε两层模型共5种湍流模型进行求解。不同湍流模型需配合相应的壁面处理方法，STAR-CCM+中提供了低y+、高y+及全y+3种壁面处理方法。根据网格和湍流模型的不同组合并匹配相应的壁面处理类型得到表4所列的算例。其中，标准k-ε模型和Realizablek-ε模型均为高雷诺数模型，仅可使用高y+壁面处理方法。Realizablek-ε两层模型仅可使用两层全y+壁面处理方法。采用Realizablek-ε两层模型和SSTk-ω两层模型求解的不同径向网格分布下沿程空泡份额示于图2。由图2可知，径向网格层数对计算结果影响较大。

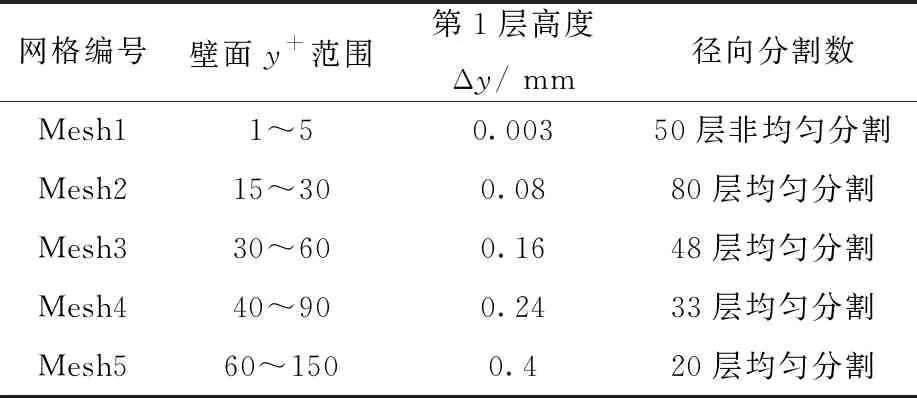
表3 径向网格分布Table 3 Radial grid distribution

结合图2a、b可发现，随着径向网格层数的增加，空泡份额计算值与实验值的偏差逐渐增大。Mesh1和Mesh2网格数量最多，但在采用Realizablek-ε两层模型的计算中未能获得收敛解。最精细的网格计算偏差反而最大，可见对于采用欧拉双流体模型进行的两相计算，并非计算域中划分的网格越多越准确。对流动沸腾现象的准确模拟很大程度上依赖于近壁区域传热传质现象的建模，加热面处第1层的网格高度过低(最小y+<40)会导致流动沸腾计算中的局部参数，尤其是近壁区空泡份额发生剧烈变化，进而影响计算的稳定性，调整松弛因子依然难以获得收敛解或计算结果出现较大的偏差。较高的第1层网格可保证气泡的瞬态行为(如产生、生长和脱离)被网格覆盖，相关参数被平均化处理，进而保证计算过程的稳定性。

表4 湍流模型、网格及壁面处理算例Table 4 Computational cases of turbulence model, grid and wall function

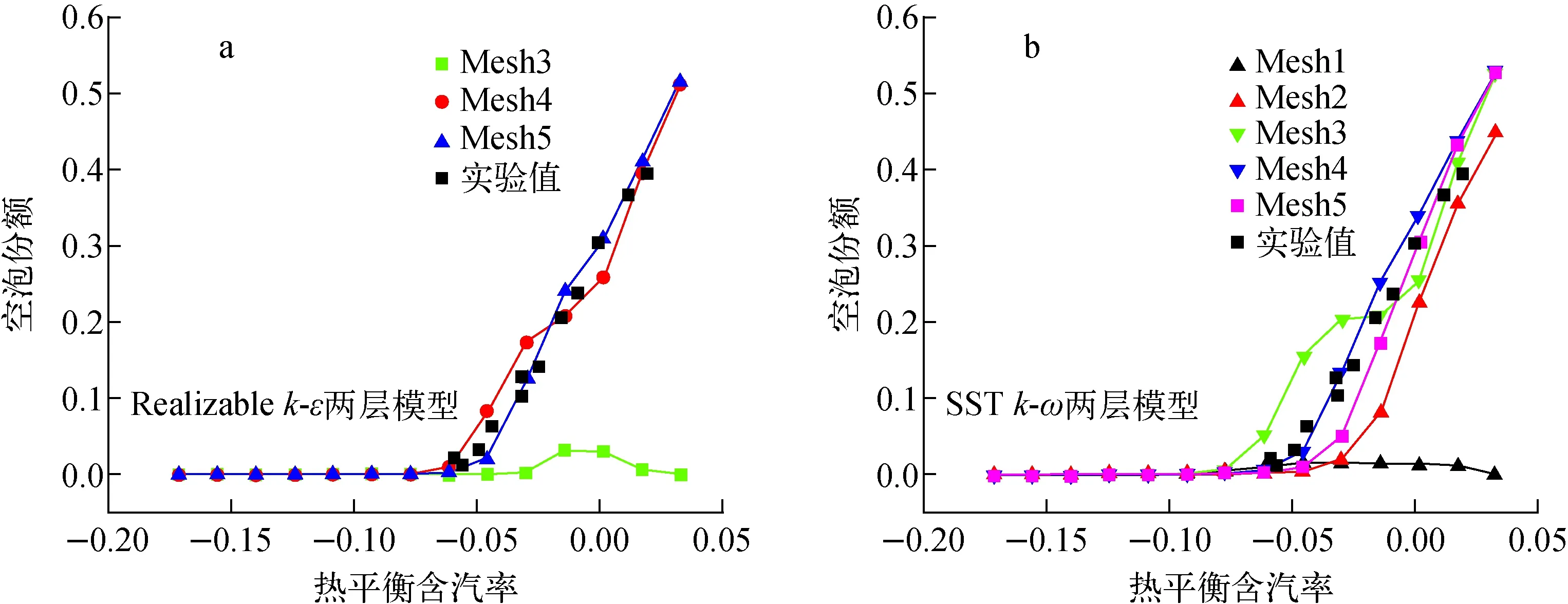
图2 不同湍流模型求解的各径向网格空泡份额的变化Fig.2 Void fraction under each grid solved by different turbulence models

保持相同的径向网格分布，不同轴向网格拉伸层数对空泡份额分布的影响示于图3。由图3可知，对当前具有较高长径比(L/D>150)的流域，轴向网格层数对空泡份额分布的影响很小，因此后续计算设置轴向拉伸层数为115，既能保证计算精度，又可减少网格量。

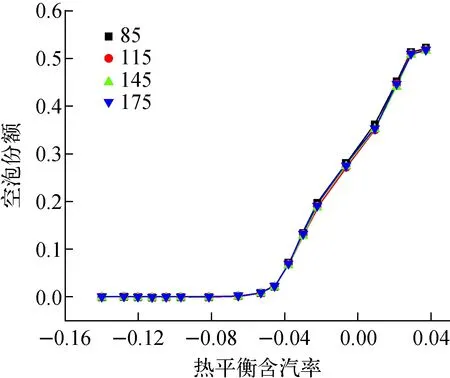
图3 轴向网格拉伸层数对空泡份额的影响Fig.3 Void fraction under different axial stretch layers

Mesh5网格尺寸下，采用不同湍流模型进行求解所得的空泡份额及壁面温度分布如图4所示。由图4可知，各湍流模型对壁面温度分布的计算结果与实验结果的差异较小，且不同湍流模型间的计算结果差异不大。标准k-ε模型对轴向空泡份额分布的计算存在较大偏差，出口处的空泡份额高于其他湍流模型，且对气相出现位置的计算与其他模型存在较大差异。Realizablek-ε模型及Realizablek-ε两层模型能很好地反映轴向空泡份额分布。

3.2 沸腾模型敏感性分析

为进行沸腾子模型的敏感性分析，将Lemmert-Chawla(LC)、Hibiki-Ishii(HI)和李权(Li)等开发的汽化核心密度模型、Tolubinsky-Kostanchuk(TK)和Kocamustafaogullari(KI)气泡脱离直径模型以及3个气泡影响面积缩放系数(1、2和4)进行组合得到表5所列算例。

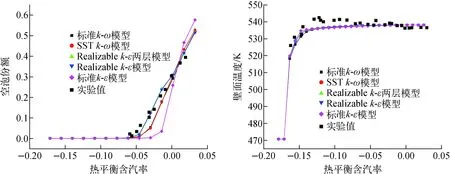
图4 Mesh5网格下不同湍流模型的计算结果Fig.4 Calculation results of different turbulence models under Mesh5

首先对不同的气泡影响面积缩放系数FA进行敏感性分析，随后分析汽化核心密度和气泡脱离直径模型的影响。

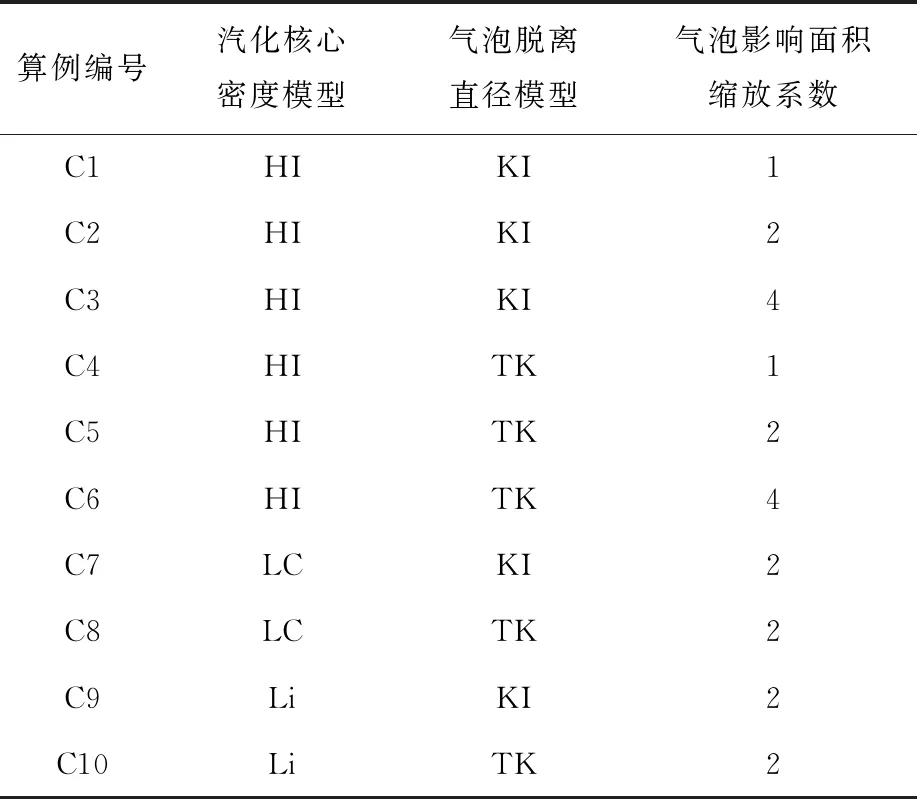
表5 壁面沸腾模型计算工况Table 5 Computational cases of different boiling models

不同模型计算结果的对比如图5所示，其中图5a为3组不同的FA对计算结果的影响，图5b为不同沸腾子模型组合的计算结果对比。由图5a可知，FA对参数分布的影响很小，计算中可取FA为2，该值由Bartolomei等[20]根据实验测得。由图5b可知，除LC-KI模型组合外，其余5组模型均能对壁面温度分布做出较好的预测。HI-KI模型组合和Li-KI模型组合对壁面温度的计算结果较为接近，LC-TK模型计算的壁面温度与实验结果最接近。此外可看出，采用基于局部过冷度得到气泡脱离直径的TK模型求解的空泡份额与实验值存在较大差异，过早地预测了气泡产生的位置，但随着空泡份额的增大，偏差逐渐减小。不同沸腾子模型组合对主流温度的计算结果在加热段的前半段差异较小，靠近出口段存在一定偏差。结合壁面温度及空泡份额分布曲线可得，两相计算中推荐采用HI-KI或Li-KI沸腾子模型组合。

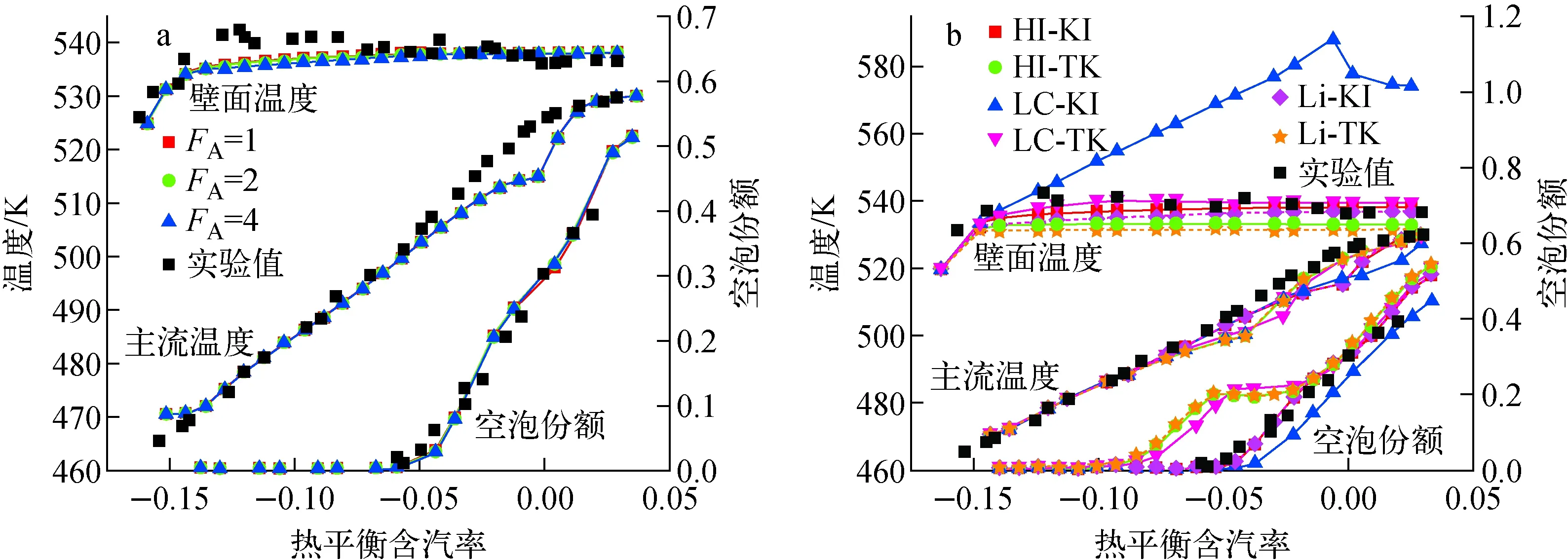
图5 不同沸腾模型计算结果对比Fig.5 Comparison of different boiling models

3.3 相间作用力模型敏感性分析

为评估相间作用力对计算结果的影响，将其分为曳力及非曳力两部分进行对比。在同一曳力模型(Tomiyama模型)下，通过不同非曳力模型组合得到表6所列算例。湍流耗散力选用Burns模型，壁面润滑力选用Antal模型，虚拟质量力采用Auton模型，升力模型为Tomiyama模型。随后，再对比7种曳力模型对计算结果的影响。

不同非曳力模型组合下的轴向参数分布对比示于图6。由图6可知，非曳力中的湍流耗散力对空泡份额分布及主流温度分布有较大影响，计算中若不考虑湍流耗散力，则会导致空泡份额升高，原因是湍流耗散力促使气泡由加热面向过冷的主流中扩散，使得更多气泡冷凝，从而降低空泡份额。而升力、虚拟质量力、壁面润滑力对轴向参数分布的影响较小。不同模型组合均能对壁面温度分布做出较好的预测。

不同非曳力模型对径向空泡份额及轴向壁面温度分布的影响示于图7。由图7可知，不考虑非曳力时，气泡会集中分布于靠近加热面处，从而引起壁面温度飞升。增加湍流耗散力后，径向空泡份额呈现展平趋势。增加升力会使空泡份额的峰值位置由壁面向主流转移。而虚拟质量力、壁面润滑力对径向空泡份额分布影响很小，可忽略不计。根据以上分析可知，采用欧拉双流体模型进行两相计算时，加入湍流耗散力及升力的影响即可获得较好的结果。

表6 相间相互作用力计算工况Table 6 Computational cases of different interaction forces

不同曳力模型的计算结果示于图8。由图8可知，对于当前工况，各曳力模型均能较好地反映出轴向空泡份额的分布，其中TY曳力模型和对称曳力模型的计算结果与实验值吻合最好。

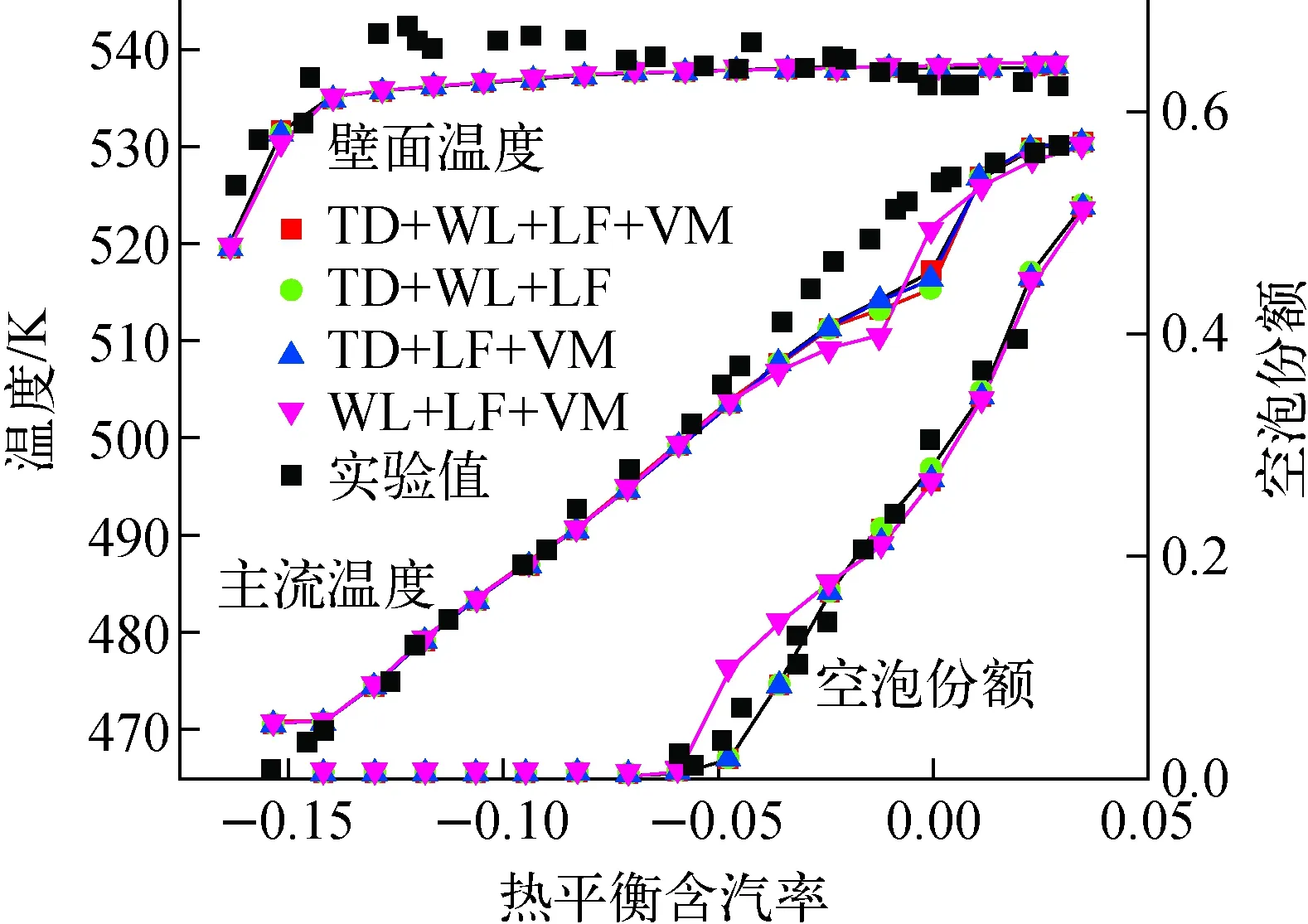
图6 不同非曳力模型组合下的轴向参数分布Fig.6 Axial parameter distribution under different non-drag force model combinations

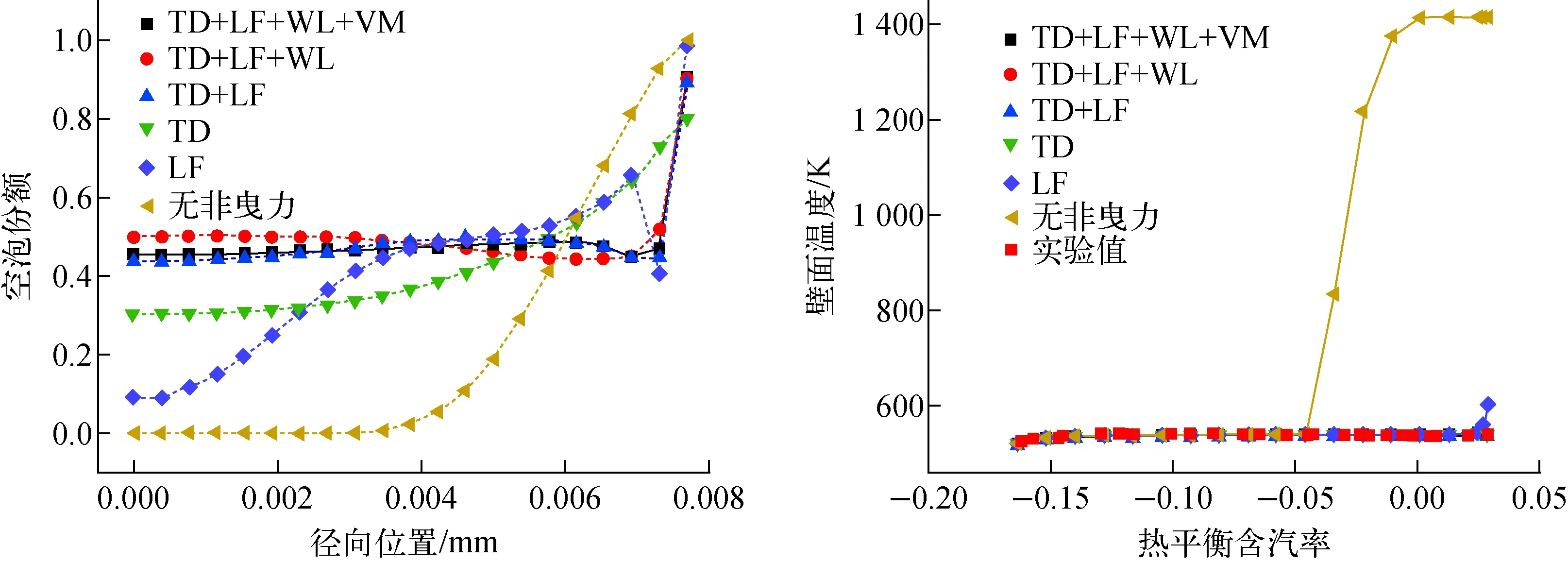
图7 非曳力模型对径向空泡份额及轴向壁面温度分布的影响Fig.7 Influence of non-drag force model on radial void fraction and axial wall temperature distribution

4 结论

本研究基于欧拉双流体模型，结合壁面沸腾模型对管内过冷流动沸腾进行了数值模拟。基于实验结果对模型参数进行了敏感性分析。通过对比分析识别出了对结果影响较大的参数并给出了推荐设置。

图8 曳力模型对计算结果的影响Fig.8 Influence of drag force model on calculation result

采用欧拉双流体模型进行过冷流动沸腾计算时，需注意加热面y+不能太低，过低的y+值会导致收敛困难或产生较大偏差，本研究中加热面y+处于40～150范围内可获得较好的计算结果。对其他工况或几何结构开展两相CFD计算时可采用文中网格敏感性分析的方法来调整加热面处网格的高度。湍流模型推荐选用Realizablek-ε模型或Realizablek-ε两层模型。壁面沸腾模型中的汽化核心密度和气泡脱离直径模型推荐选用HI-KI或Li-KI模型组合。各相间作用力中对计算影响较大的有湍流耗散力及升力，而虚拟质量力及壁面润滑力的影响可忽略。