百千瓦级空间锂冷快堆系统热工安全特性研究

金 钊，王成龙，刘 逍，代智文，田文喜，秋穗正，苏光辉

(西安交通大学 核科学与技术学院，陕西 西安 710049)

随着空间探索任务要求的不断提高，空间探测器将面临更为极端的空间环境，传统太阳能供电难以满足深空探测的需要，大功率空间核反应堆已成为未来太空能源的主要发展方向[1]。

空间核电源的能量转换方式可分为动态能量转换和静态能量转换。对于大功率空间核电源，静态能量转换效率低，提高功率输出时将极大增加辐射散热器的质量。动态能量转换由于转换效率高，辐射器面积相对较小，由太阳热流引起的系统功率波动也极为有限。目前，动态能量转换如斯特林循环、布雷顿循环等已成为大功率空间核反应堆设计采用的主要能量转换方式。斯特林循环结合液态金属冷却反应堆可实现百千瓦级的功率输出，如SP-100型空间反应堆系统设计方案[2]。

本文针对百千瓦级锂冷快堆耦合斯特林循环的空间核电源系统，开发系统热工水力分析程序，对特定事故工况进行安全分析，并为此类空间核电源的设计提供参考。

1 百千瓦级空间锂冷电源

SP-100型空间核反应堆电源是美国最初为“星球大战”(SDI)开发的轨道电源，任务可用轨道为2 000 km、倾角为28°的圆形轨道，而后也考虑将其作为星表能源，设计目标是提供100～1 000 kW功率输出[3-7]。SP-100将主要部件及子系统模块化，其反应堆和屏蔽散热系统可与动态转换装置连接，满足使用者的体积限制及功率水平[8]。

SP-100的斯特林动态转换系统主要由堆芯、斯特林电机、电磁泵和热管式辐射器组成[9]。系统由两回路组成，一、二回路分别采用锂(Li)和钠钾合金(NaK)作为冷却工质。一回路Li工质经过堆芯加热后与斯特林热端换热。斯特林机组采用冗余设计，以确保动力安全。

二回路NaK工质与斯特林冷端换热后通过三级辐射器排放废热。热管辐射器中，工质首先与钾热管蒸发段对流换热，最终热量通过与热管冷凝段连接的C-C翅片辐射至宇宙空间。堆芯由燃料棒和安全棒组成，燃料棒芯块采用氮化铀(UN)。堆芯通用布置如图1所示，可改变燃料组件数量实现不同等级的功率输出。针对SP-100，大多研究集中于单一部件的分析建模[10]，对其系统整体建模研究以及瞬态分析较少。本文开发了可应用于大功率锂冷快堆耦合斯特林电机的系统程序，以SP-100为对象进行建模仿真，研究其热工安全特性。

图1 SP-100堆芯通用布置Fig.1 SP-100 core general layout

2 数学物理模型

图2 堆芯区域划分示意图Fig.2 Schematic of core area division

系统由堆芯、管道、斯特林发电机以及热管辐射器组成。为简化计算，堆芯沿径向划分分区，各分区计算1个平均通道(图2)，忽略各分区之间换热。通道由冷却剂、芯块、反射层及气腔组成，沿轴向划分控制体。忽略芯块轴向导热，考虑反应性反馈。对各部件控制体建立微分方程，求解采用改进吉尔算法，对斯特林模型采用四阶龙格库塔公式求解。

2.1 堆芯物理热工模型

堆芯的功率瞬变计算采用点堆中子动力学方程[11]。考虑各通道流量以及燃料元件功率各不相同，采用并联多通道模型，每个通道代表中子物理特性、热工水力特性相似的一类元件。

对于燃料元件，考虑内热源、芯块导热，能量方程如下：

(1)

对于气隙及包壳，能量方程如下：

(2)

式中：ρ为密度，kg·m-3；c为比热容，J·kg-1·K-1；T为温度，K；λ为热导率，W·m-1·K-1；r为径向坐标，m；q为内热源，W·m-3；t为时间，s-1；下标u表示燃料芯块。

对于各通道内液态金属工质，将其简化为一维不可压缩流动换热模型，方程组如下。

质量方程：

(3)

动量方程：

(4)

能量方程：

(5)

式中：z为轴向坐标，m；W为质量流量，kg·s-1；A为通道流通面积，m2；f为摩擦阻力系数；De为通道水力直径，m；h为冷却剂对应比焓，kJ·kg-1；q为热流密度，kJ·m-2；U为加热周长，m。

2.2 斯特林发电机模型

斯特林发电机模型包括冷热端壁面、气体工质、回热器等部分。对于气体工质采用理想气体绝热微分方程组进行计算。斯特林冷热端壁面有如下热平衡方程：

(6)

(7)

式中：ρIn、ρOut分别为热、冷端包壳材料密度，kg·m-3；TIn、TOut分别为热、冷端包壳内壁温度，K；Tf为气体温度，K；AIn、AOut分别为热、冷端截面面积，m2；λIn、λOut分别为热、冷端材料热导率，W·m-1·K-1；δIn、δOut分别为热、冷端包壳壁面厚度，m；cIn、cOut分别为热、冷端包壳材料比热容，J·kg-1·K-1；ΠIn、ΠOut分别为热、冷端换热周长，m；TH为热源温度，K；TC为热阱温度，K；Hf为气体与壁面的换热系数，W·m-2·K-1；ηST为斯特林效率。

加热器、冷却器与回热器为有限温差传热，具有相似控制方程，循环换热量如下：

Qi=hiAw,i(Tw,i-Tg,i)(1/n)

(8)

式中：Q为循环换热量，W；h为工质与壁面换热系数；Tw为内壁面温度，K；Tg为气体温度，K；n为机轴转数；i为所划分的控制体编号。

实际回热器有回热损失，定义有效度ε，ε为实际循环回热量与理想循环回热量之比。忽略回热器导热热阻，有：

(9)

式中：Awg为换热面积，m2；A为工质自由流动面积，m2；St为斯坦顿数，对于工质氦气，St=0.46Re-0.4Pr-1。

回热器轴向热损失Qloss可由下式计算：

(10)

式中：λr为回热器外壳处热导率，W·m-1·K-1；Ar为回热器横截面积，m2；lr为回热器长度，m；Th、Tc分别为热、冷侧平均温度，K。

2.3 辐射散热器模型

辐射散热器模型分为回路管网模型及热管辐射单元模型。管网结构如图3所示，管网模型中假设流体不可压缩，忽略散热。

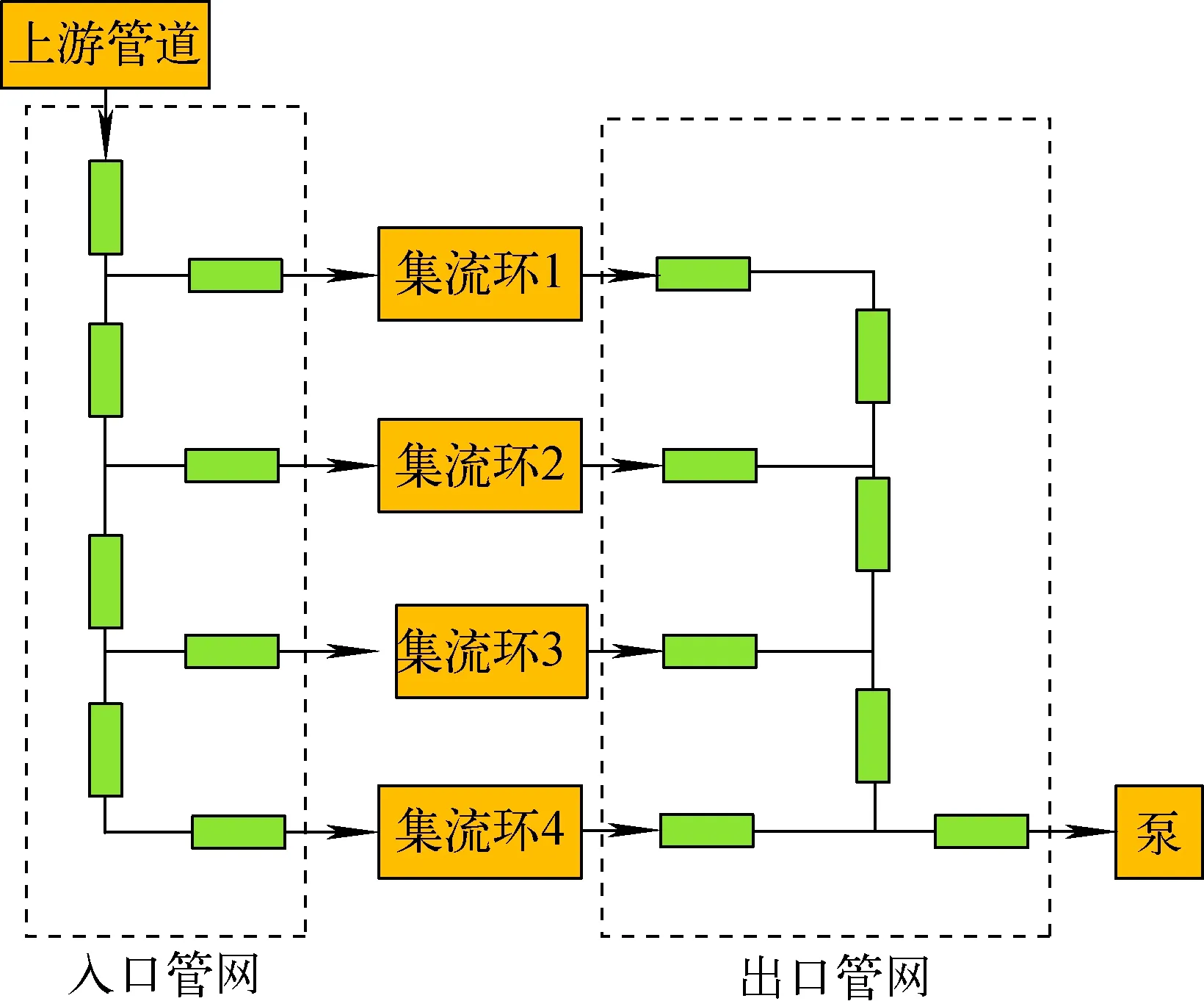
图3 回路式辐射器管网结构Fig.3 Pipe network structure of loop radiator

根据守恒关系可得如下方程：

(11)

(12)

(13)

图4给出典型辐射单元结构。辐射单元由热管及焊接在热管上的翅片组成，排出热量有3部分：翅片两侧辐射换热(Q1)，热管翅片散热(Q2)，裸露的热管散热(Q3)。

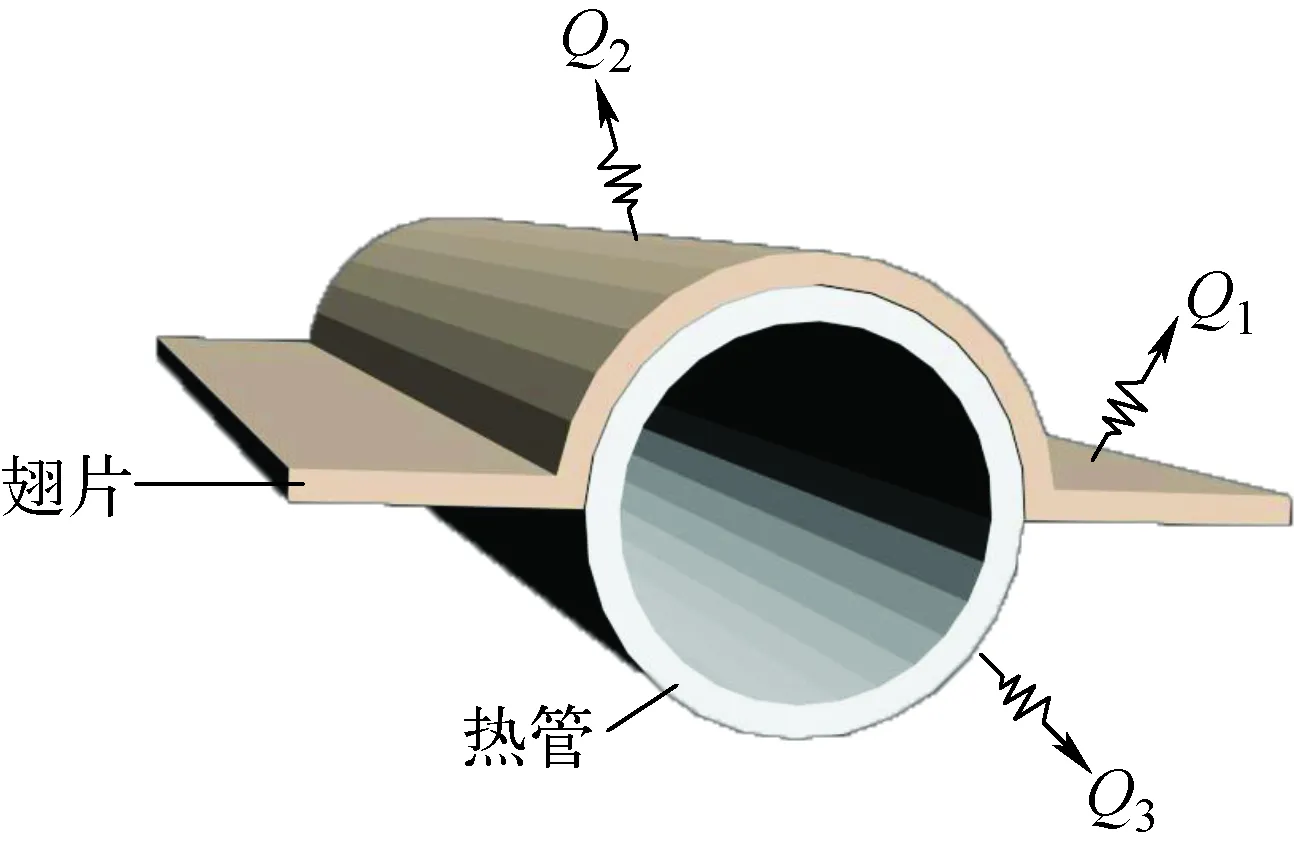
图4 辐射单元示意图Fig.4 Schematic of radiator unit

热管模型包括管壁导热、吸液芯内工质流动传热、蒸汽流动3部分。忽略吸液芯流动影响，采用纯导热模型求解吸液芯及管壁区域，假设蒸汽区域温度均匀。

管壁区域控制方程如下：

(14)

吸液芯区域控制方程如下：

(15)

(16)

式中：C为体积热容，J·m-3·K-1；x为径向坐标，m；K为导热系数，W·m-1·K-1；y为轴向坐标，m；下标w及ws分别表示管壁及吸液芯，eff指折算后的吸液芯参数，l及s分别表示工质及吸液芯。

翅片模型参考文献[12]。

3 结果与分析

RE-1000为美国Sunpower公司为NASA设计的1 kW原型样机[13]，利用RE-1000的实验结果对斯特林模型进行验证。RE-1000的主要参数参考文献[14]。表1列出计算结果与实验数据对比，最大相对误差为17.1%。由表1可见，该模型可准确分析斯特林模型的性能。

表1 参数模型计算结果与实验数据对比Table 1 Parameter comparison of model calculation result with experimental data

3.1 稳态结果分析

根据文献[7]给出的堆芯及辐射器进出口温度设计值，考虑堆芯在实际热功率输出为455 kW时，系统稳态计算结果列于表2，计算值与设计值误差较小，并将作为后续瞬态计算的初始条件。

3.2 事故工况分析

1) 反应性引入事故

本计算中，1 s内向堆芯引入0.1 $反应性，保护系统不动作。图5示出堆芯及斯特林功率瞬态响应特性，堆芯功率在200 s内迅速升高至880 kW。由于功率升高引起堆芯温度升高(图6)，整体的负反应性反馈(图7)使得堆芯功率逐渐下降(图5)，最终稳定在470 kW，斯特林功率也逐渐升高至稳定。由于堆芯功率的剧烈升高，热点温度迅速升高，200 s内增加约110 K，并未超过芯块熔点3 120 K[15]，具有较大的安全裕度。

表2 稳态计算结果Table 2 Steady state result

图5 反应性引入事故下斯特林及堆芯功率的变化Fig.5 Change of Stirling and core power under reactivity insertion accident

对于二回路，堆芯额外正反应性的引入导致对热量排出能力的要求提高，辐射器平均温度迅速上升(图8)，排出多余热量为一回路提供足够冷却。虽然系统特性可将堆芯热量有效移除，但额外反应性引入导致堆芯热点温度迅速上升，对于更高的反应性引入，可能产生冷却剂局部沸腾，因此仍需额外防护以减少此类事故的发生。

图6 反应性引入事故下辐射器及堆芯进出口流体温度的变化Fig.6 Fluid temperature change of radiator and core inlet and outlet under reactivity insertion accident

图7 反应性引入事故下热点温度及堆芯总反应性变化Fig.7 Change of hot point temperature and total core reactivity under reactivity insertion accident

图8 反应性引入事故下辐射器热管冷凝段温度的变化Fig.8 Temperature change in condensation section of radiator heat pipe under reactivity insertion accident

2) 热阱丧失事故

若二回路辐射器发生部分热管失效，将导致系统热阱丧失。计算中考虑30%的热管破裂失效，系统无保护动作。

热点温度的变化与反应性变化趋势一致，如图9所示。受到二回路热阱丧失影响，一回路平均温度升高，燃料元件及堆内结构的负反应性反馈使得总体反应性下降，最低可降至-0.005 $，反应堆及斯特林功率也随之下降(图10)。最终，总反应性与堆芯功率逐渐震荡至稳定，堆芯功率稳定在410 kW。

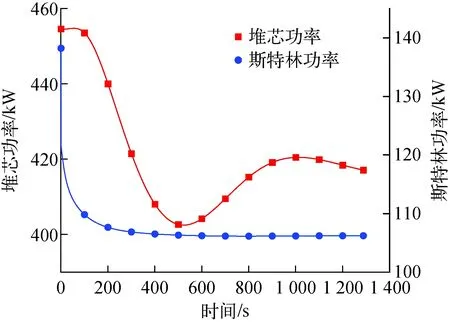
图10 热阱丧失事故下斯特林及堆芯功率变化Fig.10 Change of Stirling and core power under loss of heat sink accident

图11示出辐射器及堆芯进出口温度的瞬态响应特性。事故发生前期，二回路侧温度迅速升高。辐射器进出口温度迅速增加，约在450 s后达到稳定，平均温度增加约50 K。在部分热管破裂后，其余部分热管温度升高(图12)，承担多余的热量排出，体现了系统安全特性。

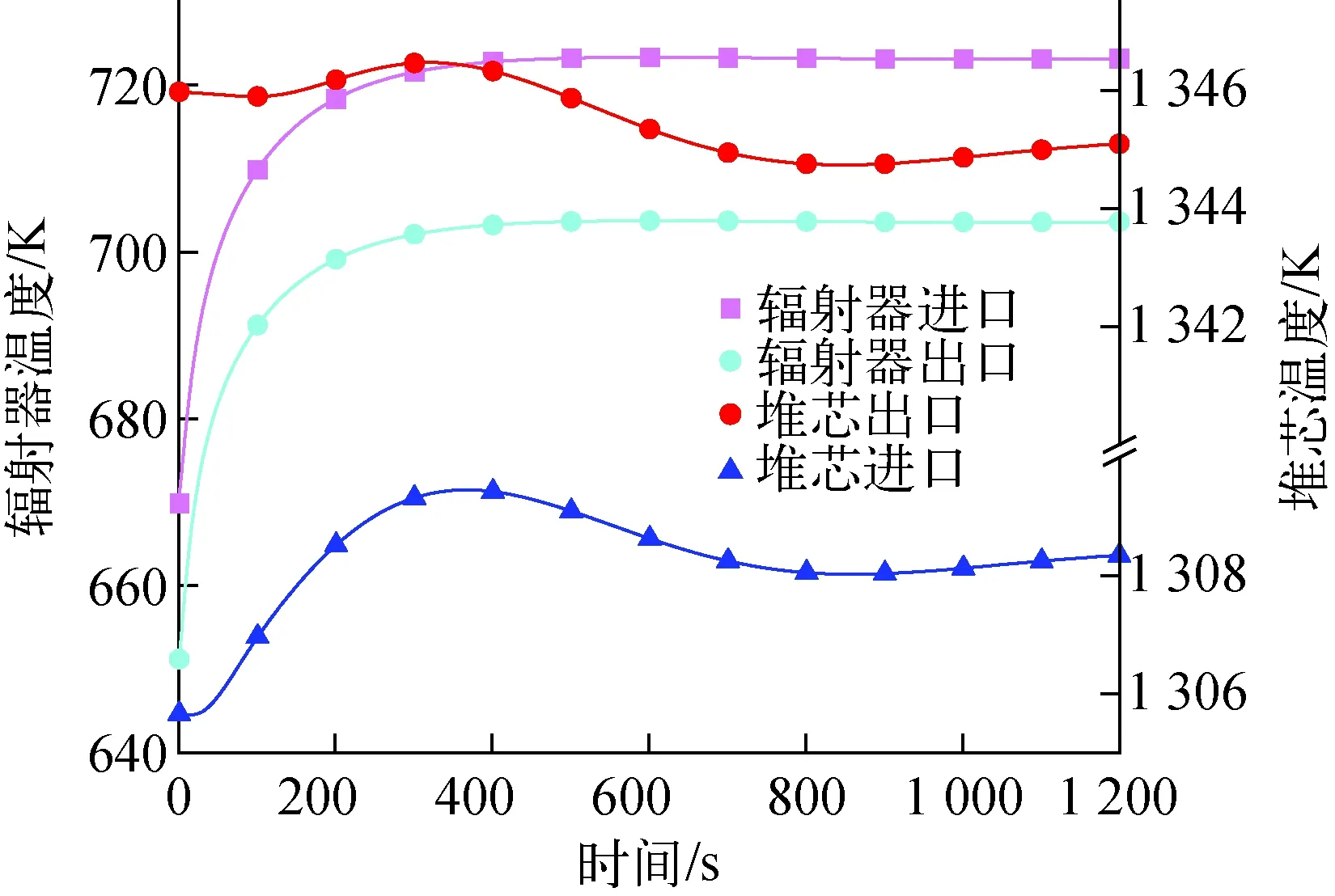
图11 热阱丧失事故下辐射器及堆芯进出口流体温度变化Fig.11 Fluid temperature change of radiator and core inlet and outlet under loss of heat sink accident

图12 热阱丧失事故下辐射器热管冷凝段温度变化Fig.12 Temperature change in condensation section of radiator heat pipe under loss of heat sink accident

整体来看，事故发生时一回路温度有一定上升趋势，出口温度变化相对于进口温度有一定延迟(图11)，堆芯总体反应性受温度负反馈效应的影响，导致堆芯功率及热点温度降低，热点温度最低降至约1 423 K。因此部分热阱丧失且无额外保护动作时，系统仍可维持正常运行，具有较高的安全特性。

4 总结

本文针对百千瓦级锂冷快堆空间核电源系统建立数学模型，并对SP-100进行了模拟仿真，得到如下结论。

1) 本文开发了空间锂冷快堆瞬态热工分析程序，利用RE-1000实验数据对斯特林模块进行校核，最大相对误差为17.3%，验证了模型的合理性。利用所开发程序针对采用斯特林循环的SP-100进行建模，进行了反应性引入事故及热阱丧失事故的计算。

2) 热阱丧失事故中，由于热管的固有安全性以及堆芯负反应性反馈的影响，可在事故发生时有效排除热量，降低堆芯功率，维持系统的正常运行，体现出系统安全特性。在反应性引入事故中，热点温度迅速升高，低于安全限值并有极大安全裕度。但仍需防止此类事故的发生，热点温度的急剧上升可能产生局部沸腾。

本文结果证明了所开发程序可准确分析大功率锂冷快堆空间核电源系统的热工安全特性，为此类系统设计优化奠定理论基础。对于更高反应性引入，可能导致锂冷却剂出现局部沸腾，此类事故分析将在后续工作中继续进行。