基于新型双滑模的永磁同步电机无传感器矢量控制

杨浩， 赵强， 杨钊， 王瑞， 朱宝全

(东北林业大学交通学院， 哈尔滨 150040)

永磁同步电机(permanent magnet synchronous motor, PMSM)具有结构简单、运行可靠、体积小、质量轻、损耗小、效率高等显著优点，在航天、新能源汽车和军事等领域得到了广泛应用。但永磁同步电机是一个集磁链、电流和转速等多变量为一体的耦合系统，使其控制十分困难[1-2]，通常采用矢量控制或者直接转矩控制,其中矢量控制通过解耦实现让永磁同步电机具有类似直流电机的控制效果，在永磁同步电机的控制系统中得到了更广泛的应用[3]。

在永磁同步电机矢量控制系统中，通常需要知道精准的转子位置信息和转速信息，相应传感器的安装存在成本、制造和安装等难题，使得目前无传感器控制技术逐渐成为研究热点[4-5]。目前获得转速信息和转子位置信息的方式主要有模型参考自适应法[6]、状态观测器[7]、扩展卡尔曼滤波器法[8]、滑模观测器[9]。其中滑模观测器对系统模型精度要求不高，对参数变化和外部干扰不敏感，鲁棒性强，成为一种广泛使用的方案，然而其在趋近运动中产生的高频抖振抑制是一个有待解决的问题[10]。文献[11] 针对传统滑模观测器存在严重的高频抖振以及转子位置和电机转速估算精度不足等问题，使用一种基于幂次趋近律的新型滑模观测器，提高了转子位置和电机转速观测精度，抑制了系统的高频抖振，但是转速突变的工况下还存在抖振。文献[12]在非奇异终端滑模面上引入分数阶微积分算子得到连续光滑的反电动势估算值，最后通过分数阶锁相环精确估算出电机转速。文献[13]设计了基于变指数趋近律和锁相环技术相结合的新型滑模观测器，此观测器能准确观测转速和转子位置，提高动态性能。文献[14]根据最优电压矢量选择判据选定开关状态，完成基于圆形电流误差边界限定形式的永磁同步电机的预测控制算法，通过仿真验证，此方法在转速阶跃时响应迅速且提高了稳态性能。文献[15]提出一种双滑模控制系统，通过新型滑模观测器来估计转子位置和转速，利用滑模转速控制器代替传统比例积分(proportional integral,PI)速度控制器，并通过低通滤波器和转子角度补偿的方法，降低了低速时的抖振问题，但该方法没有实现电机转速变化的工况。

综上所述，在PMSM中采用双滑模控制很少有深入的研究。为了降低系统的抖振并达到更好的控制效果，现基于滑模控制原理[16-17]、滑模观测器原理[18-19]，提出一种新型双滑模控制(new type double sliding mode control,NDSMC)的方法，用高阶滑模观测器来替代传统的滑模观测器，用新型的滑模转速控制器来代替传统的PI转速控制器，来降低系统存在的抖振，提高PMSM控制系统的动态和稳态性能。最后，通过MATLAB/simulink仿真结果对比分析转速和转子位置估计的精度，验证系统的有效性，以及对高频抖振的抑制效果，以期为永磁同步电机的设计提供理论基础。

1 新型滑模速度控制器的设计

1.1 永磁同步电机数学模型

为了便于控制器的设计，建立表贴式永磁同步电机在dq旋转坐标系下的数学模型为

(1)

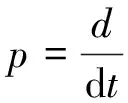
为了得到更好的控制效果，采用id=0的矢量控制，则数学模型变为

(2)

1.2 新型滑模速度控制器趋近律

传统滑模控制器一般采用指数趋近律，指数趋近律为

(3)

式(3)中：-εsgn(s)为等速趋近项；s为滑模面；-qs为指数趋近项。

由于传统指数趋近律中sgn为符号函数，会导致严重的抖振，采用饱和函数代替符号函数，饱和函数为

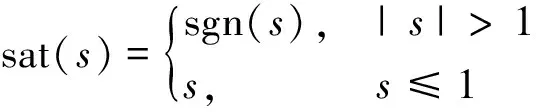
(4)

由于积分运算具有消除高频信号的作用，所以为了能够进一步抑制抖振，在传统指数趋近律的基础上再加入积分项，从而得到新的趋近律为

(5)

式(5)中：ε>0；q>0；KW、Kf为待设计参数。

V=0.5S2

(6)

对式(6)求导，得

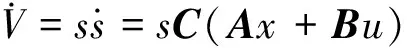
(7)

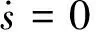
u=-(CB)-1[CAx-εsat(s)-qs-KW|ρ|sat]

(8)

将式(8)代入到滑动模态可达性条件得

(9)

1.3 新型滑模速度控制器设计

基于式(5)的趋近律设计控制器，根据式(2)定义永磁同步电机系统的状态变量：

(10)

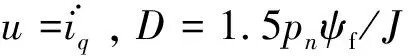
(11)

定义滑模面函数为s=cx1+x2,其中c>0为待设计参数。对其求导可得

(12)

从而由式(4)和式(11)可得q轴参考电流为

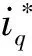
(13)

从式(13)可以看出，控制器包括高阶积分项，不仅可以削弱抖振现象，还可以消除系统的稳态误差，提高系统的控制效果。

2 高阶滑模观测器的设计

2.1 永磁同步电机数学模型

在静止αβ坐标系下，表贴式永磁同步电机的数学模型可表示为

(14)

式(14)中：iα、iβ为永磁同步电机定子电流在α、β轴的分量；uα、uβ为滑模观测器的控制输入；Eα、Eβ分别为扩展反电动势在α、β轴的分量。式(14)中永磁同步电机反电动势满足：

(15)

式(15)中：ωe为电角速度；ψf为永磁体磁链；θr为转子位置角度。

由式(15)可知，转子的位置和速度信息都包含在反电动势中，因此，可以通过对反电动势进行观测，从而得到转子位置和转速。

2.2 高阶滑模观测器设计

首先已有的传统滑模观测器为

(16)

(17)

为解决上述问题，使用一种高阶滑模观测器，即在上述传统滑模观测器基础上，加入高阶积分项。由于积分有类似低通滤波器的作用，不仅可以降低对低通滤波器的使用，还可以用来提高永磁同步电机的无速度传感器控制的精度。所设计的高阶滑模观测器具体如下：

(18)

式(18)中：ξ和σ为待设计的增益系数。由于高阶滑模观测器也加入了积分运算，可以起到很好的降抖振作用。

将式(16)和式(18)做差可得电流的观测误差为

(19)

(20)

由式(19)和式(20)可得

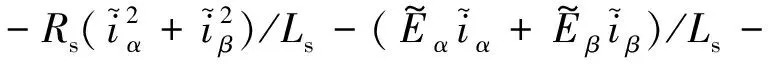
(21)

为了保证观测器收敛，需满足pV1<0,可得

(22)

(23)

(24)

(25)

由式(24)和式(25)得

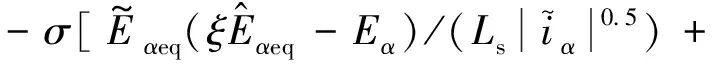
(26)

为保证观测器收敛，需满足pV2<0。则可得

(27)

由式(22)和式(27)可知，通过选择较大的参数值即可保证观测器收敛，再通过实际的观测效果来进行数值的调整，以提高控制精度。

3 仿真验证与结果分析

为了验证设计的基于新型双滑模永磁同步电机矢量控制方法的有效性，根据系统框图(图1)，在MATLAB/simulink中搭建了如图2所示的基于新型双滑模PMSM无位置传感器控制仿真模型。仿真采用表贴式三相永磁同步电机为被控对象，具体参数为：定子电阻Rs=2.875 Ω；定子电感Ls=8.5 mH；永磁体磁链ψf=0.175 Wb；转动惯量J=0.001 kg/m2；极对数Pn=4；控制器参数为：c=60；ε=200；q=200；KW=16 000；Kf=-200；k=300；ξ=100；σ=10。

idref、iqref为d、q轴参考电流;iabc为三相电流;为观测器估计转速;为观测器估计转子位置图1 新型双滑模的PMSM无速度传感器矢量控制系统整体框图Fig.1 New type double sliding mode sensorless vector control system for PMSM

图2 基于新型双滑模PMSM无位置传感器矢量控制仿真模型Fig.2 New type double sliding mode sensorless vector control system for PMSM

设置工况为：在空载条件下，初始额定转速由500 r/min在0.2 s时增加到800 r/min，并且在0.4 s时，突然增加5 N/m的负载。仿真步长为2×10-7，仿真时长为0.6 s。并在同样的工况下，采用传统比例积分(proportional integral controller, PI)转速控制+传统滑模观测器(sliding mode observer, SMO)和传统滑模转速控制(sliding mode control, SMC)+传统滑模观测器与所设计的新型双滑模控制进行对比，通过仿真得到转速响应曲线、误差曲线、转子实际位置与估计以位置曲线以及误差曲线，如图3～图7所示。

由图3和图4可以看出，在空载启动的时候，PI-SMO控制的超调量约为80 r/min并伴有多次的抖振后才能达到期望转速；SMC-SMO控制的超调量约为120 r/min，并需要约0.05 s才能达到期望转速；其中NDSMC控制的超调量约为75 r/min，并且可以迅速达到期望转速并进入到稳态。在稳态过程中，PI-SMO控制和SMC-SMO控制的转速估计误差为5～10 r/min。NDSMC控制下的转速估计误差仅为1～2 r/min。在负载突变时，PI-SMO控制虽然转速突变不大，但是伴有很大的抖振，当再次进入稳态时，电机的实际转速约为795 r/min，与期望转速相差约为5 r/min。SMC-SMO控制转速骤降76 r/min，观测器估计的转速也伴有抖振，电机的实际转速最终会稳定在802 r/min。NDSMC控制在负载突变时，转速骤降了67 r/min，最终电机的实际转速会稳定在801 r/min，稳态误差最小。从转速的角度总体来看，电机在NDSMC控制下具有更好的动态和稳态性能，转速估计更加准确。在负载突变时，虽然转速会骤降，但是会迅速恢复到期望转速，并不伴有严重抖动，稳态误差最小。

图3 转速响应曲线Fig.3 Speed response curve

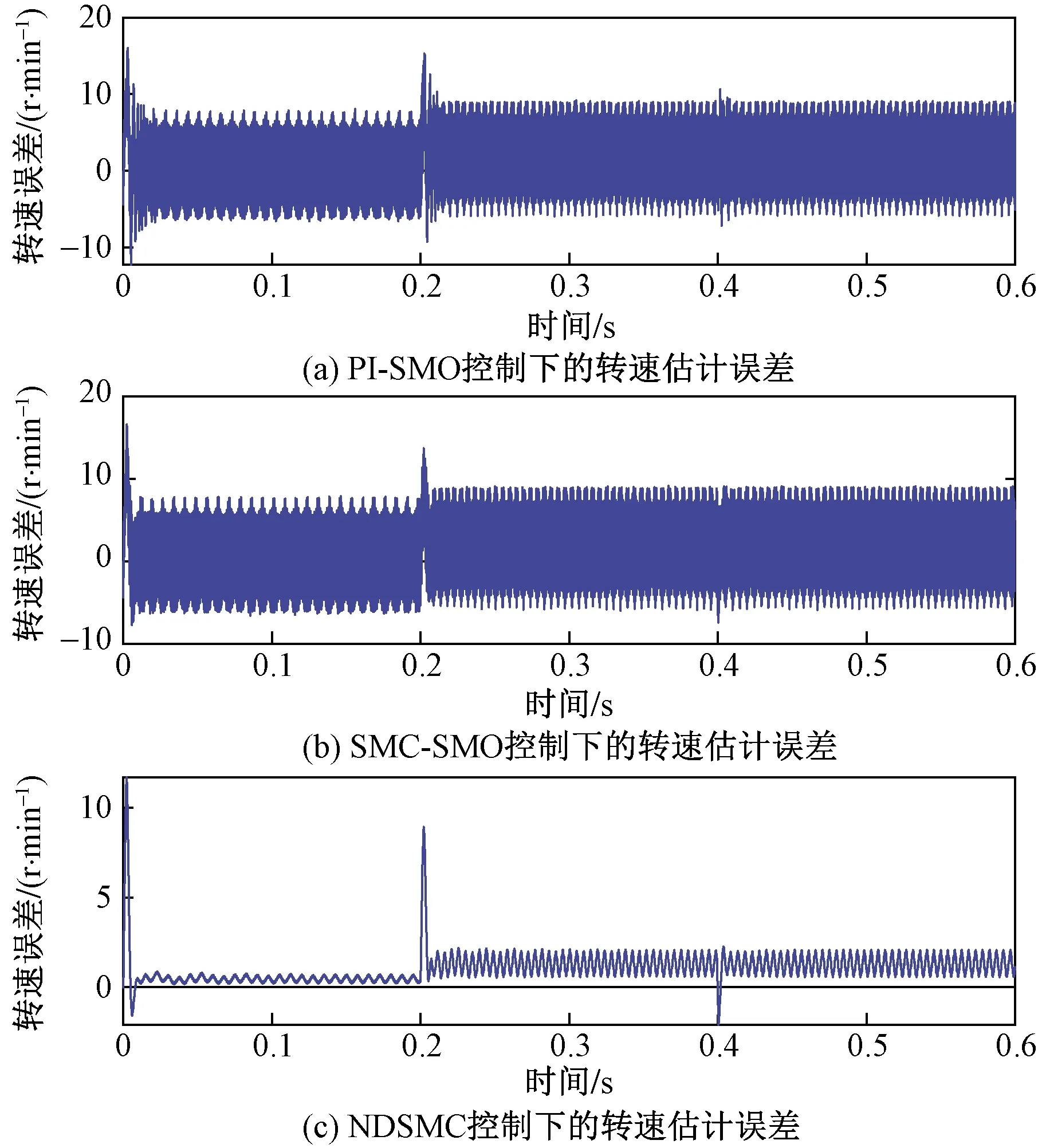
图4 转速估计误差曲线Fig.4 Speed estimation error curve

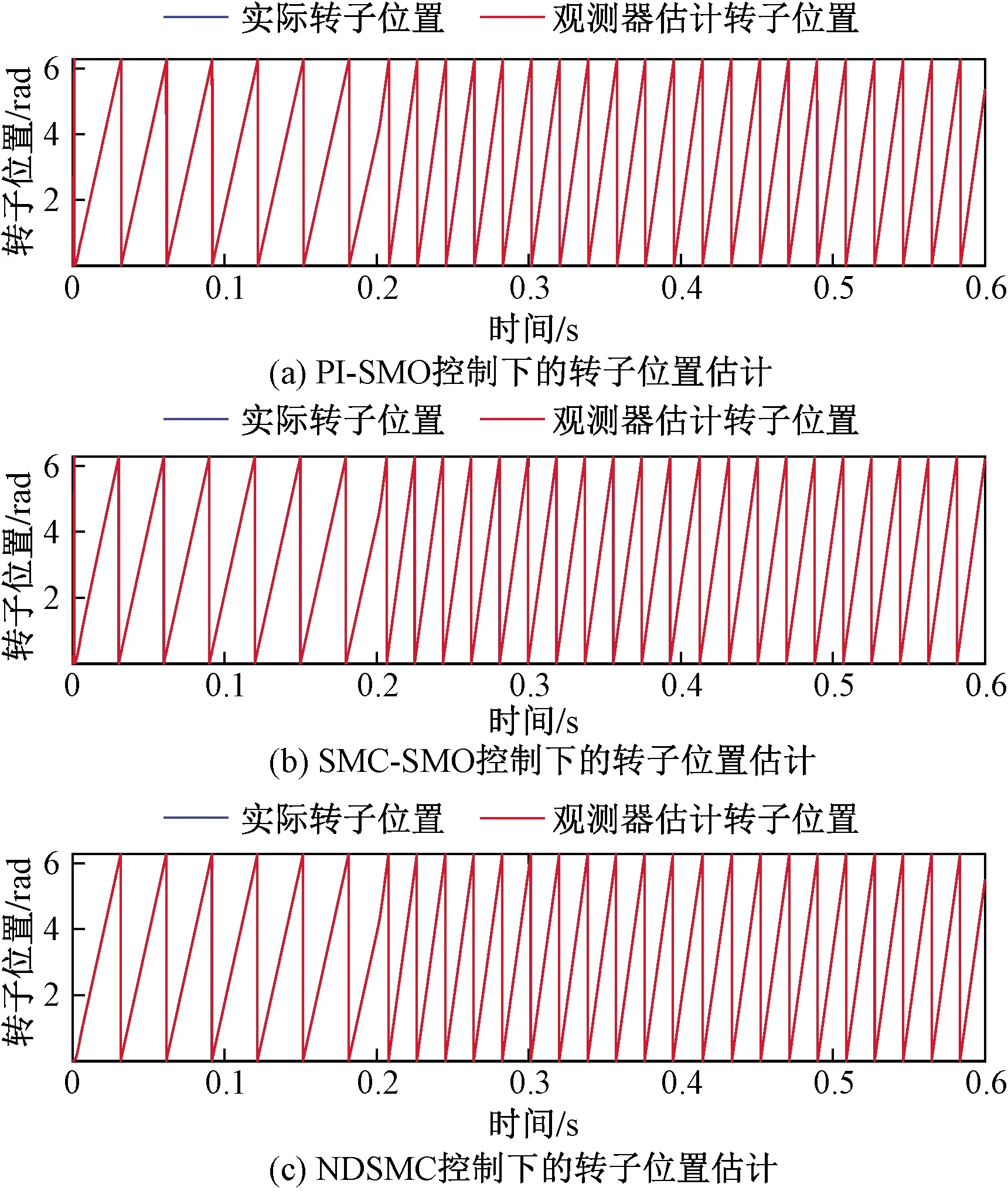
图5 转子位置估计Fig.5 Rotor position estimation

由图5～图7可知，对比PI-SMO控制和SMC-SMO控制，NDSMC控制下可以更加快速准确地观测转子位置。其中PI-SMO控制和SMC-SMO控制伴有高频的抖振，估计精度差，而NDSMC基本无抖振，精度较高。

由上述仿真结果可知，提出的新型双滑模的永磁同步电机无传感器控制与PI-SMO控制和SMC-SMO控制相比，所提的新型双滑模控制方式有效的抑制了系统的抖振和超调，在转速突然变化或者负载突然变化时，该系统具有较好的动、稳态性能。

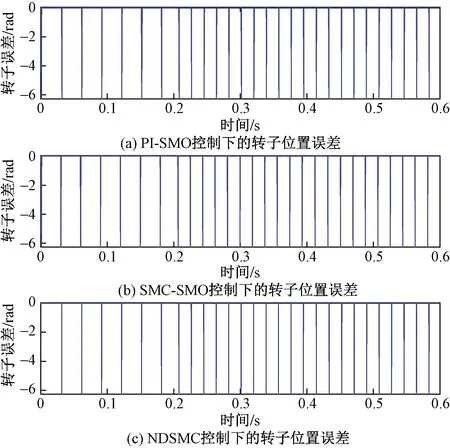
图6 转子位置误差Fig.6 Rotor position error

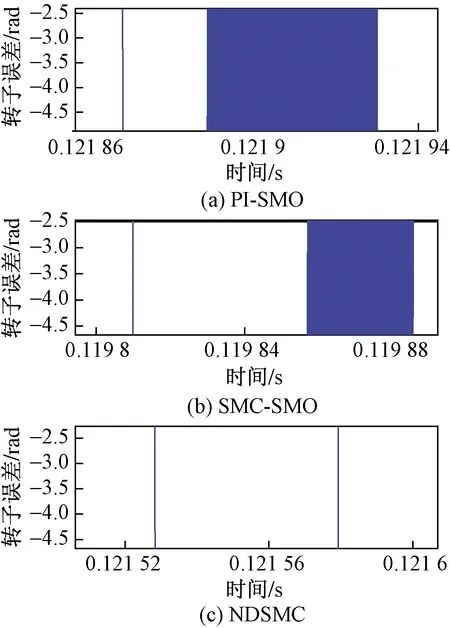
图7 转子位置误差放大图Fig.7 Enlarged drawing of rotor position error

4 实验验证

为了验证改进双滑模控制方法的可靠性，将此控制方法应用在电机快速原型仿真控制平台上进行实验，实验平台如图8所示。实验得到的实际转速由于受振动噪声的影响，使得传感器测量的实际转速约有2 r/min的误差，但观测器估计的转速基本无抖振。超调量控制较好，转子位置估计也较为精准，如图9所示。

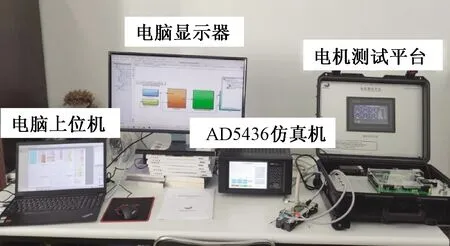
图8 硬件平台Fig.8 Hardware platform

图9 实验图像Fig.9 Experimental result

5 结论

提出了一种基于新型的双滑模控制的控制方法，通过MATLAB/simulink将该方法在永磁同步电机无传感器矢量控制系统中进行仿真研究，并与传统控制方式进行对比。通过仿真结果对比分析以及实验验证，得到以下结论。

(1)设计基于高阶滑模观测器的新型滑模观测器与速度控制器，从理论上分析与传统滑模观测器与传统滑模控制相比存在的优势，可以有效地降低系统的抖振。

(2)在MATLAB/simulink中建立了基于新型双滑模PMSM无位置传感器矢量控制仿真模型，通过仿真结果可以看出，新型的双滑模控制下具有更好的稳态特性。

(3)通过与其他控制方式进行对比，新型的滑模控制能更好地降低系统的抖振，同时能够更加精准地估计电机转速和转子位置，具有良好的控制品质，具有一定的使用意义。