改进的带参考信号盲源分离算法
张延良, 张玉, 张伟涛
(1.河南理工大学物理与电子信息学院, 焦作 454150; 2.西安电子科技大学电子工程学院, 西安 710071)
盲源分离算法(blind source separation, BSS)是在源信号统计独立,且源信号和传输信道等先验知识均未知的情况下,仅根据观测到的混合信号将各个源信号分离出来的技术[1-2]。盲源分离研究始于20世纪80年代,短短二十几年间,其相关理论和实际应用快速发展[3]。目前如何将感兴趣的信号从混合信号中有效地提取是信号处理领域的研究热点和重点之一。
带参考信号的盲源分离算法也被称为约束独立成分分析算法(constrained independent component analysis, CICA)[4],是提取感兴趣信号最有效的方法。许多情况下,源信号的特性并不是一无所知的。源信号的一些特征如载波频率、调制方式等先验信息是已知的,将这些先验信息引入到独立成分分析(independent component analysis, ICA)中可以用于感兴趣信号的提取[5]。相对于ICA,CICA算法更适合实际应用。例如,在提取语音信号时可能只对某些信号感兴趣,只需要根据感兴趣信号的某些特征来进行提取,显然CICA算法更有优势。
目前CICA算法已经被广泛应用于机械故障诊断[6-7]、语音识别[8]、图像处理[9]、通信[10]等领域。近年来,不少学者将CICA算法应用在生物医学方面。王凯等[11]提出了一种实时约束独立成分分析方法,在去除心电伪迹上得到了较好的效果;Shi等[12]提出了一种基于多目标优化框架的约束时空ICA 方法,对感兴趣信号的恢复能力在一定程度上得到了提高。但在这些应用中,提取信号与源信号之间还是存在较大误差,因此研究如何减小提取信号与源信号之间的误差具有重要意义。
为了CICA算法在其应用中有更好的提取效果,现提出直接将先验信息耦合到基于负熵的目标函数中形成一个新的目标函数,再使用拉格朗日乘子法对新的目标函数优化,使其更准确向感兴趣信号方向收敛,以此来减小误差。
1 盲源分离算法
盲源分离是用以分析多维数据的线性分析算法,试图将一组随机变量表示成统计独立变量的线性组合[13],它的数学模型为:假设L个源信号s(t)=[s1(t),s2(t),…,sL(t)]T,通过M个传感器接收,得到观测信号x(t)=[x1(t),x2(t),…,xM(t)]T,忽略噪声后可得出源信号s(t)和观测信号x(t)之间的关系表达式为
x(t)=As(t)
(1)
式(1)中:A为一个M×L的混合矩阵。原问题则转化成根据观测信号x(t)选定一个目标函数,使用优化算法对该目标函数进行优化得到最优的分离矩阵w,可以得到分离信号y(t)与观测信号x(t)之间的关系表达式为
y(t)=wTx(t)
(2)
把式(1)代入式(2)中,可得
y(t)=wTAs(t)
(3)
由式(3)可知,分离信号y(t)相当于是源信号是s(t)的一个有效估计,所以盲源分离算法的实质就是求一个最优的分离矩阵w。
2 传统的CICA
为提取感兴趣信号,目标函数的选择很关键,负熵可以反映信号的非高斯性大小,因此选择快速ICA算法中基于负熵的目标函数,但是负熵的计算非常困难,常用非线性函数J(y)来近似:
J(y)=[E{G(y)}-E{G(v)}]2
(4)
式(4)中:y为分离的源信号;v为一个具有零均值和单位方差的高斯向量;G(·)为任何非线性函数;E(·)为非线性函数的期望值。
算法的目的是最大化目标函数,但是当目标函数达到最大值时每一个源信号都有被输出的可能性,所以要提取感兴趣信号可以将感兴趣信号的先验信息作为约束加入算法中,则CICA的框架定义为
maxJ(y)=[E{G(wTx)}-E{G(v)}]2
(5)
s.t.
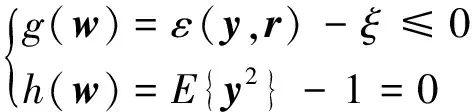
(6)
式中:s.t.为约束条件,包括g(w)和h(w)两种约束;ε(y,r)表示提取信号与参考信号的测量度,ε(y,r)=E{(y-r)2};ξ为设置的阈值,阈值的设置应该注意,如果阈值的选择过大可能会收敛到其他的源信号,相反如果阈值设置过小则收敛不到任何信号,因此阈值的设置需要谨慎。等式约束h(w)来确保目标函数J(y)和分离矩阵w有上界。
CICA算法中的参考信号应该具备以下两个条件。
(1)具备感兴趣信号的特性。这是参考信号存在的重要原因,例如,在提取胎儿心电信号时,参考信号只需要反映胎儿心电信号的某些特征即可,不用是全部特征。
(2)参考信号是非高斯性信号或者可以转换为非高斯性信号[14]。ICA算法以数据的非高斯性为基础,将目标函数的非高斯性进行最大化来寻找最优分离矩阵[15]。CICA算法是在ICA算法上发展起来的,因此CICA算法可以看成是对一个以负熵为目标函数进行约束优化的问题,然后将对比函数的非高斯性进行最大化来寻找最优分离矩阵。在ICA算法中加入参考信号是引导算法的收敛方向。因此参考信号是非高斯性信号或者可以转换为非高斯性信号才会改变算法的收敛方向。
参考信号的设计有许多种,在进行实验时脉冲法是使用最多的一种方法。脉冲法是将感兴趣信号的先验信息的脉冲信号作为参考信号,这也就说明了脉冲法满足第一个条件。此外,脉冲信号是方波序列本身具有非高斯性,因此满足第二个条件。感兴趣信号与参考信号之间的测量度越小,那么分离结果就越精确。源信号与它自身的接近度是最大的,但往往源信号是未知的,因此只能利用其先验信息近似的设计参考信号。
3 改进的CICA


(7)
s.t.

(8)
通过引入松弛因子z可以将不等式约束g(w)≤0转化为等式g(w)+z2=0。利用拉格朗日乘子法来解决上述的约束优化问题,该框架下的增广拉格朗日函数L(w,μ,λ)为


(9)

利用类牛顿算法可以得到分离矩阵w的学习算法为
w←w-η(L2)-1Γ1
(10)
式(10)中:η为学习率;L2为Hessian矩阵;Γ1为L(w,μ,λ)对w的一阶导数。为了对算法的进一步简化,可以将L2近似为Γ2RXX-1,那么近似后的分离矩阵w学习算法可以定义为

(11)
式(10)中:RXX为观测信号的协方差矩阵;Γ1、Γ2分别为L(w,μ,λ)对w的一阶导数和二阶导数:
Γ1=2aρE{x(t)g′(y)}-(2b+μ)E{x(t)(y-
r)}-λE{x(t)y}
(12)
Γ2=2aρE{g″(y)}-2b-μ-λ
(13)
式中:a=1/[ε(y,r)+1],b=[E{G(y)}-E{G(v)}]2/[ε(y,r)+1]2,G(y)为任意的非线性函数,取值G(y)=lg[cosh(y)];g′(y)为G(y)的一阶导数,g′(y)=tanh(y);g″(y)表示G(y)的二阶导数,g″(y)=1-tanh2(y);ρ=E{G(y)}-E{G(v)}。
基于梯度下降算法可以得到拉格朗日乘子的迭代公式为
μ=max{0,μ+γg(w)}
(14)
λ=λ+γh(w)
(15)
对改进的带参考信号盲源分离算法步骤如下。
(1)对观测信号进行去均值、去白化得到处理后的数据。
(2)根据感兴趣信号的先验知识来设计参考信号r。
(3)用均匀分布随机数初始化分离矩阵w并对w进行标准化。
(4)初始化拉格朗日乘子λ和μ。

4 实验分析
4.1 仿真实验
为展现算法的有效性,对改进算法进行仿真实验,选取5个相互独立的信号作为实验的源信号,源信号的函数为

(16)
式(16)中:f1=50 Hz;f2=610 Hz;f3=540 Hz;s1、s2和s3为3个周期信号。s4为均值是0标准差是1的标准正态分布随机数;s5为[-1,1]的均匀分布随机数;s4和s5统称为噪声信号;N表示噪声函数的取样长度;k的取值为1~N。本实验的采样点为500(201~700)。在提取期望源信号时所运用到的参数设置为:拉格朗日乘子λ、μ和惩罚因子γ的初始值为1,阈值ξ为1.75,学习率η=1,最大的迭代步长为200。
通过两组仿真实验(提取源信号s1和提取源信号s2)对本文提出的改进算法与文献[16]提出的算法进行性能比较。利用信噪比和均方误差来衡量其性能,衡量标准如下。
(1)信噪比。若源信号与其对应的分离信号分别为si和yi,则两者之间的信噪比(signal-noise ratio, SNR)表示为

(17)
根据信噪比的定义可以判断SNR越大表明信号功率越大,说明算法的分离性能越好。
(2)均方误差。均方误差(mean-square error, MSE)是衡量两组数据的偏差程度,yi为分离信号,si为源信号,N为采样点数,衡量标准为

(18)
源信号s1到源信号s5如图1所示。
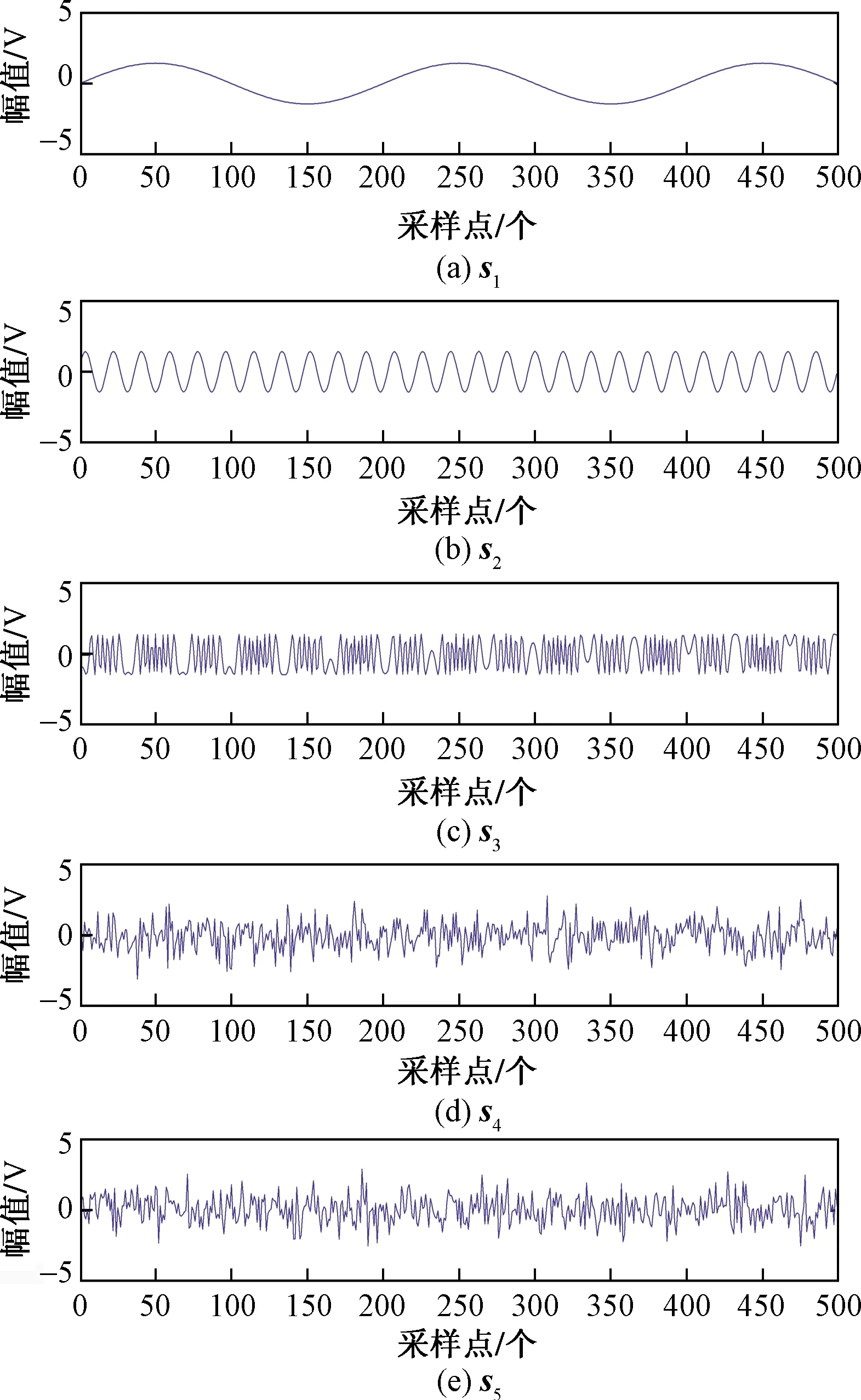
图1 源信号Fig.1 Source signal
将5个独立的源信号进行混合,混合矩阵A为[-1,1]的均匀分布随机数,混合后的信号如图2所示。

图2 混合信号Fig.2 Mixed signal
本组仿真试验运用改进的算法来提取源信号s2,设计参考信号时采用第2节所提到的脉冲法。一般情况下,感兴趣信号的周期、初始相位和脉冲宽度是脉冲法所需要的先验信息。根据源信号s2的先验信息设计参考信号r1周期为1/f2,初始相位设置为1,脉冲的宽度为8,参考信号r1和提取信号y1如图3(a)所示。
为了验证参考信号对算法分离性能的影响,可以改变参考信号的某些值以观其效果,如改变参考信号的初始相位或者脉冲的宽度,设计参考信号r2周期为1/f2,初始相位设置为3,脉冲的宽度为8,参考信号r3周期为1/f2,初始相位设置为1,脉冲的宽度为10,参考信号r2、r3和提取信号y2、y3如图3(b)和图3(c)所示。
由图3可以看到,利用参考信号r2和参考信号r3分离出的信号和真实源信号都有所不同。可以看出改变参考信号的初始相位和脉冲宽度会影响算法的分离效果,只有根据源信号的先验信息设计的参考信号才能正确提取感兴趣信号。
本组仿真实验进行1 000次最后求均值。文献[16]改进的算法和本文改进算法性能比较如表1所示。
由表1可知,本文改进算法在均方误差和信噪比上都有提高,可以进一步说明提出的算法有效。
为了试验的完备性,用改进的算法分离源信号s1,参考信号的设计同样采用第二节所提到的脉冲法,则参考信号周期为1/f1,初始相位设置为2,脉冲的宽度为100。r1为参考信号,y1为提取信号,s1为源信号,提取效果如图4所示。

图3 提取信号s2效果图Fig.3 The effect picture of extract signal s2

表1 性能评估
同样,为了衡量改进算法分离源信号s1的误差,利用信噪比和均方误差来计算,本组仿真实验进行1 000次最后求均值,文献[16]改进的算法和本文改进算法性能比较如表2所示。
由表2可知,本文改进的算法在均方误差和信噪比上都稍有提高,进一步的说明该算法的有效性。

图4 提取信号s1效果图Fig.4 The effect picture of extract signal s1

表2 性能评估
4.2 滚动轴承故障诊断实验
以滚动轴承故障诊断为例,采用改进的CICA方法对其验证,利用如图5所示的试验台对滚动轴承外圈单一故障进行试验,试验轴承安装在主轴上,实验机主轴与变频电机用联轴器连接,通过调节变频电机转速来模拟主轴旋转。

图5 试验台Fig.5 Test bench
试验轴承型号为D276126NQ1U的双半内圈三点接触球轴承,其轴承外圈内径为142.9 mm,外径为190.0 mm,宽度为33 mm,球个数为10,球径为24.6 mm,节径为166.45 mm,采样频率为20 000 Hz,采样时间为10 s。根据轴承外圈故障频率计算公式在1 000 r/min转速下的外圈故障频率为127 Hz。
传感器采集的外圈混合信号如图6所示,从图6中可以看到采集到的信号杂乱无章,看不到任何有效的故障特征。根据滚动轴承的理论外圈故障频率(f=127 Hz),现产生一方波序列作为参考信号。将参考信号和观测信号同时作用于改进的CICA算法中,可得到提取信号。参考信号r与提取信号y如图7所示。
为了验证提取信号的正确性,对提取的故障信号进行Hilbert包络谱分析,结果如图8所示,从图8可以看到,在125~130 Hz处幅值较高,计算的轴承外圈故障特征频率127 Hz在其区间,因此可以说明CICA算法准确地提取了故障特征。

图6 外圈故障采集信号Fig.6 Outer ring fault acquisition signal

图7 参考信号r与提取信号yFig.7 Reference signalrand extracted signaly

图8 提取信号包络图Fig.8 Extract signal envelope
5 结论
为减小CICA算法中源信号和提取信号之间的误差,提出了一种新的CICA算法。该算法在标准对比函数中,耦合了含有先验信息的测量度函数,以此得到了新的目标函数;然后在新目标函数上采用拉格朗日乘子法,最终有效地获得了最优分离矩阵。在仿真实验中,与其他算法相比,该算法具有较小的误差。在滚动轴承故障诊断实验中,该算法正确提取了滚动轴承外圈故障特征,进一步说明了该算法的有效性。

