一类低先验信息度的先验分布选择研究

王 维

(常州大学 阿里云大数据学院， 江苏 常州 213164)

贝叶斯统计自诞生以来，在许多领域都得到了应用，如多元统计判别分析、计量经济学和地理信息学等[1]。在贝叶斯统计中，如何确定先验分布是一个重要的研究课题，一旦确定了先验分布，剩下的问题几乎都可以通过计算机辅助解决。目前，国内外关于先验分布的研究大致可以分为以下3类：

(1)对先验分布选择标准的探讨。此类研究主要关注在有多个先验分布可供选择的情况下，如何选出最优的先验分布。周巧娟等[2]提出利用似然比检验方法选择先验分布，李勇等[3]提出当参数θ的可选先验族Γ={π：π(θ)为θ的先验}，且π(θ)的先验分布为u(π)时，可以选取u(π)下均值对应的先验。

(2)不同先验分布对参数Bayes估计的影响比较。王敏[4]比较了3种不同类型的先验分布对艾拉姆咖分布中参数估计的影响；邸俊鹏等[5]比较了当先验分布为正态分布时，方差的变化对结果的影响。

(3)特定模型中先验分布的确定。Gelman提出了一种确定分层模型先验分布的方法[6]，之后又讨论了Logistic回归模型中先验分布的选择[7]。

本文关注的是上述第二类问题的研究。综合分析相关文献，已有研究还存在以下可以改进的方面：

(1)对先验分布的讨论不够细致。如王敏[4]仅讨论了先验分布为伽马分布、共轭先验分布和无信息先验分布的情况，并没有考虑先验分布中参数的变化对结果的影响；邸俊鹏等[5]只考虑了先验分布为正态分布的情况。

(2)研究结果的指导性不强。具体表现在两个方面：第一，大多数研究讨论的都是无信息条件下先验分布的选择问题，事实上，这类问题已经有较为成熟的研究成果，而且在实践中对于待估参数一无所知的情况并不常见；第二，缺少对所选先验分布合理性的说明。

随着统计计算技术的长足发展，后验分布及各种后验量的计算已经不再是使用Bayes分析的障碍，合理性成为了先验分布的选取需要考虑的首要因素。遗憾的是，很少有文献对先验分布的选取原因予以说明，这难免会令人对其结果的准确性与可靠性产生怀疑，也不利于真正理解和掌握相关问题的解决方法。基于上述分析，本文从换位思考的角度出发，分析了研究者在低先验信息度时可能选择的先验分布，并讨论了样本量、先验分布的类型与方差对估计结果的影响，对这类问题的解决具有一定的参考价值。

1 先验信息分类和先验分布选择标准

1.1 先验信息的分类

在实践中，可能需要考虑各种各样的先验分布，Gelman等[7]提出先验分布可以分为3种类型：第一，无信息先验分布(Noninformation Prior Distribution)，适用于没有任何先验信息的情况；第二，高信息先验分布(Highly Information Prior Distribution)，适用于针对先验分布中参数的精确信息可得的情况；第三，适度信息多层次先验分布(Moderately Information Hierachical Prior Distribution)，适用于由已有数据不能对先验分布中的参数做出较好的估计，需要对参数再做一个先验的情况。

借鉴上述分类思想，根据信息量的多少，本文将先验信息也分为3类：

第一类，无先验信息。此时没有任何关于先验分布的信息。

第二类，高先验信息。此时先验分布已知或已知分布的类型，其中的参数可以根据先验信息估计得到。

第三类，低先验信息。此时已知先验分布的部分信息，但信息量很少，无法推断出先验分布的具体形式，有时甚至连先验分布的类型都无法确定，例如只知道先验分布的均值。

高先验信息时，所需的信息均已知，只需按部就班进行计算即可。无先验信息下的研究已经较为成熟，如使用Bayes假设、Jeffreys先验等，而且实践表明，无信息先验虽不是唯一的，但它们对Bayes统计推断结果的影响都很小，很少对计算结果产生重大影响。低先验信息是实践中经常遇到的情况，一般而言，我们很难知道先验分布的具体形式，但又不至于对待估参数一无所知。Assaf等[8]提供了一个随机边界模型中参数估计的例子，他们指出该模型中的一个参数ui(用于刻画企业的实际表现与最优表现间的差距)是一个非负的随机项，因此先验分布应是只有一侧的分布，如指数分布、半正态分布、Gamma分布和其他截断分布。

1.2 先验分布的选择标准

(1)合理性。是先验分布选择的首要标准。在统计计算技术飞速发展的当下，这一点显得更为重要。先验分布的合理性来源主要有两个：

①有经验事实作为支撑。经过大量的实践，某些特定问题的先验分布已经有了较为公认的结论。如一般认为彩电的平均寿命使用倒Gamma分布IG(α,λ)作为先验分布是恰当的，其中α>0、λ>0是两个待定的参数。

②能说明从可选先验分布族中选择不同的先验分布对结果的影响很小，很少对计算结果产生重大影响，此时选择可选先验分布族中的任何分布都是合理的，如无信息时先验分布的选择。

(2)便利性。在满足合理性的条件下，可能仍然有大量的分布可供选择，考虑到研究的成本，应优先考虑我们熟知的基础的分布，缩小研究范围，简化分析计算，方便人们使用。

(3)针对性。不同的问题往往有不同的特点，在某些领域中，部分分布可能具有更好的特性，如平滑性更好。因此，在满足合理性与便利性的要求后，还可以根据研究问题的特点，选出最优的先验分布。

2 问题分析

本文以《高等数理统计》中的一类问题为对象，探究一类低先验信息情况下先验分布的选择对参数Bayes结果的影响。

设事件A发生的概率为θ，即P(A)=θ，某人为了估计θ而做了n次独立观察，发现事件A出现了X次，并且根据相关经验，可以认为θ的概率密度函数在[0,1]区间上是连续且单调递减的，试对θ进行估计。在这个问题中，已知θ的先验分布定义域为[0,1]，且概率密度函数在[0,1]区间上单调递减。但是，仅根据这些信息我们甚至无法推断出先验分布的类型，是一个典型的低先验信息问题。

从换位思考的角度出发，可能会有以下几种看法：

(1)虽然已知θ的概率密度函数在[0,1]区间上连续且单调递减，但信息量仍然太少，和无先验信息的情况差别不大，因而考虑使用无信息先验分布。

(2)事件A发生的次数X～b(n,θ)，其共轭先验分布为Be(a,b)，为了便于计算，可以选取Be(a,b)作为先验分布，但要注意a、b的取值应满足单调性的要求。

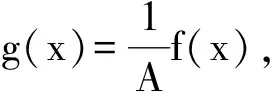
先验分布的选择包括分布类型选择和参数选择。前者根据看法的不同选择无信息先验分布(均匀分布)、共轭先验分布、截断指数分布和截断正态分布4种类型。后者对应于不同的方差，方差反映了研究者对所选先验分布的信心，一般认为其值越大，越接近于无信息先验分布。

基于上述讨论，本文设定了不同的分布类型、参数和样本量，以观察对结果的影响。

3 试验设计

根据贝叶斯统计的相关结论，设待估的参数为θ，其参数空间为Θ，先验分布为π(θ)，根据样本得到的似然函数为p(x|θ)，那么后验分布π(θ|x)可以表示为

即

π(θ|x)∝π(θ)p(x|θ)。

为了方便讨论，设定损失函数为平方损失，此时θ的Bayes估计δπ(x)为后验分布π(θ|x)的均值，即δπ(x)=E(θ|x)，定理的证明可以查阅相关文献，这里不再赘述。

当后验分布较为复杂时，后验量的计算通常比较困难，此时一般通过统计方法得到后验分布的模拟分布，从模拟分布中抽样，再根据蒙特卡罗方法得到后验分布特征数的估计。

本文采用Jim[10]所推荐的办法来估计后验分布的均值，具体步骤及R语言代码如下：

(1)确定后验分布概率密度函数的定义域，构造向量p，使得p的第一个分量和最后一个分量恰好为定义域的两端，且p的各分量将定义域划分为若干个部分；

(2)得到似然函数在p各分量上的取值；

(3)得到先验分布概率密度函数在p各分量上的取值；

(4)计算似然函数和先验分布概率密度函数取值的乘积，并将其转化为概率；

(5)依据上一步得到的概率，从p中进行抽样。

p=seq(0,1,length=500)

post=dunif(p,0,1)*dbeta(p,2,3)

post=post/sum(post)

ps=sample(p,10000,replace=TRUE,prob=post)

x<-mean(ps)

4 试验结果

为验证前文的假设，共设计了7种先验分布，具体见表1。

表1 试验分布的部分特征数

4.1 样本量对结果的影响

极大似然估计法以X/n(样本均值)作为θ的估计，为便于在不同样本量时进行比较，取适当的X值，使得样本均值分别为0、0.2、0.4、0.6、0.8、1.0，将样本量分为n=5、n=15、n=30三组，7种先验分布结果的标准差见表2。

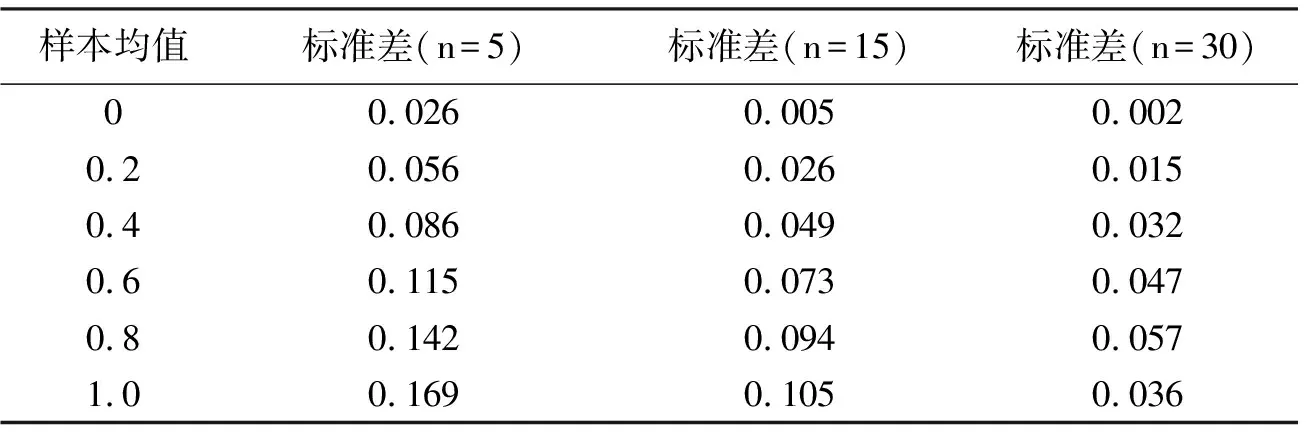
表2 不同样本量下7种先验分布结果的标准差

为了方便总结规律，将表2的结果绘制成图1。

图1 表2结果的可视化

从图1可以看出：①7种先验分布的标准差与样本均值有关，且不同样本量下标准差随样本均值的增加呈现不同的变化特点；②固定样本取值时，样本量大的标准差总是小于样本量小的标准差。上述结果说明，当样本量足够大时，先验分布的类型与参数对结果的影响很小，采用不同先验分布的结果相差不大。

4.2 先验分布类型对结果的影响

表3 3种先验分布的结果

从表3可以看出，3种先验分布的测算结果相差很小，说明当样本量与方差相同时，先验分布的类型对结果几乎不会造成影响。

4.3 先验分布方差对结果的影响

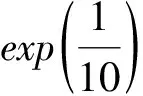
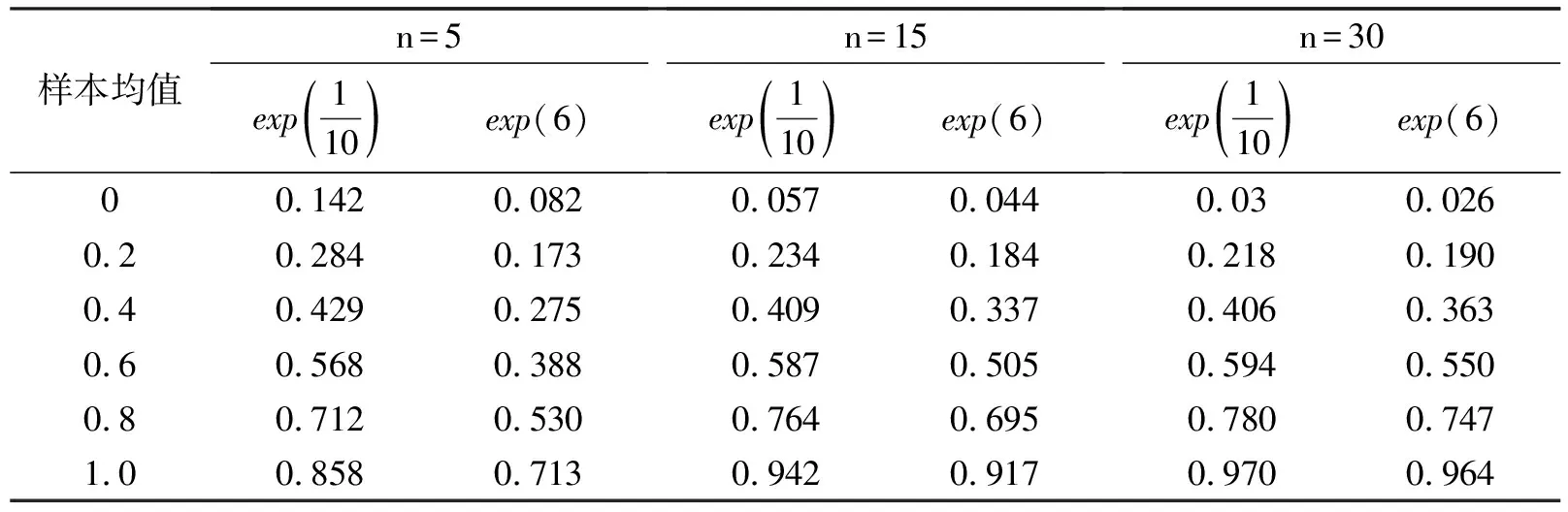
表4 分布类型为指数分布的结果

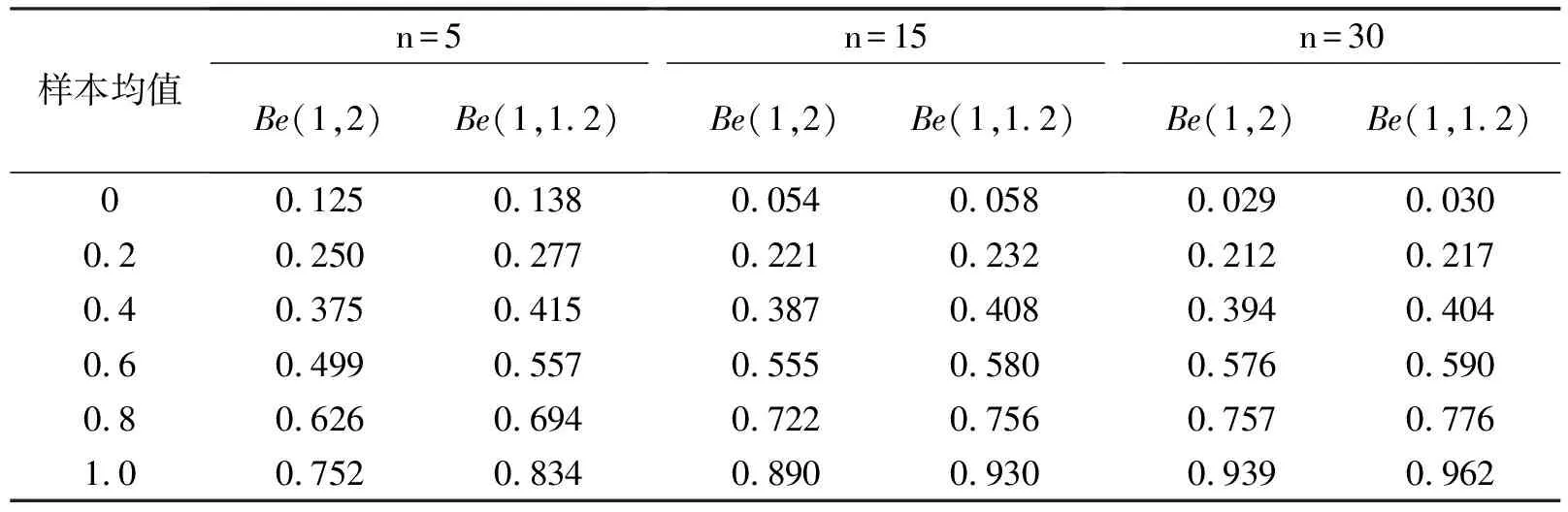
表5 分布类型为贝塔分布的结果

从表4和表5可以看出：①固定分布类型和样本量时，两种分布的结果均存在差异；②贝塔分布组两种分布的结果差异更小，说明方差相差越多，结果的差异也越大。

5 结论与建议

本文使用计算机模拟的方式研究了一类低先验信息度情况下先验分布的选择问题，根据控制变量法分别讨论了样本量、分布类型与分布方差对结果的影响。结果表明：当样本量较大时，先验分布的选择对结果影响不大；样本量较小时，先验分布类型对结果几乎无影响，先验分布方差相差越多，结果的差异越大。

基于上述结论，当样本量较大时，选择满足已知条件的先验分布即可。当样本量较小时，首先考虑合理性与便利性，确定待选先验分布的范围，然后计算各种分布对应的结果，最后根据研究问题的特点，检索相关资料或请教有关专家以选出最合适的先验分布。