一类具有扩散和时滞的HIV模型的动力学分析

蒲武军

(陇南师范高等专科学校 数学系， 甘肃 陇南 742500)

近年来，病毒已经严重威胁到人类社会的健康，许多不同领域的学者都在利用各种方式致力于宿主病毒感染过程中的机制和动力学行为研究，当然，对于艾滋病病毒(HIV)的研究也不例外，许多应用数学工作者提出了一系列的HIV模型，并进行了详细的研究，获得了许多好的结果[1-4]。最近，文献[5]提出了一个具有时滞的HIV模型：

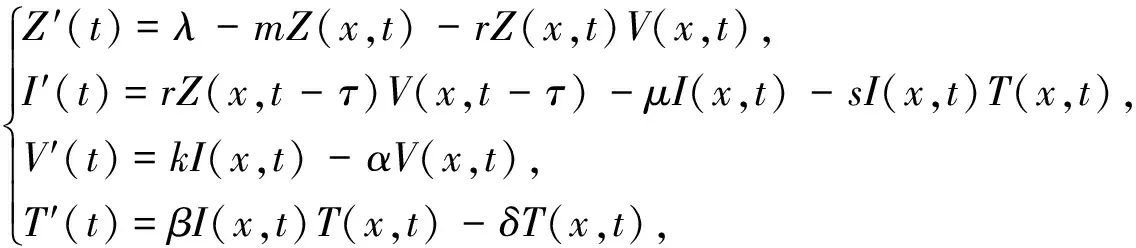
(1)

讨论了系统(1)各类平衡点的局部渐近稳定性，研究了具有状态和控制时滞的最优控制问题，并进行了数值模拟。显然，对于HIV模型的研究，时滞是一个不可忽视的因素，与此同时，病毒粒子的扩散更应该受到重视，因此，探讨具有扩散的病毒模型便是其中的一个热点问题，并取得了一系列好的结果[6-10]。上述相关模型的研究，主要集中在感染率函数的变化以及免疫反应的引入，感染率函数主要集中在双线性函数、Holling-II型反应函数、Beddington-DeAngelis反应函数、Crowley-Martin反应函数以及更一般的反应函数方面，而且，许多时候人们忽视了病毒的流动性，实际上病毒是可以自由移动的，它们的运动遵循Fickian扩散。受系统(1)和上述研究的直接启发，本文拟讨论如下具有时滞的反应扩散HIV模型：

(2)

初值条件为

Z(x,θ)=φ1(x,θ),I(x,θ)=φ2(x,θ),V(x,θ)=φ3(x,θ),

(3)

齐次Neumann边界条件为

(4)

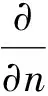
1 解的整体存在性和适定性

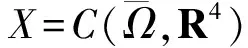
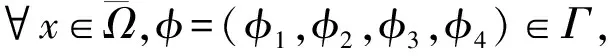
F3(φ)(x)=kφ2(x,0)-αφ3(x,0),

F4(φ)(x)=βφ2(x,0)φ4(x,0)-δφ4(x,0),

则F在Γ上是局部Lipschitz的，于是系统(2)—(4)可改写成如下的抽象泛函微分方程：

(5)

其中φ=(Z，I，V，T)T，φ=(φ1，φ2，φ3，φ4)T，Aφ=(0，0，dVΔV，0)T。显然，根据标准的存在性理论[11]，系统(5)在[0，Tmax)上存在一个唯一的局部解，Tmax是系统(5)的最大存在时间[12]，且0=(0，0，0，0)T显然是系统(2)—(4)的下解，因此，Z(x，t)≥0，I(x，t)≥0，V(x，t)≥0，T(x，t)≥0。

λ-γ(Z(x,t-τ)+I(x,t)+T(x,t)),

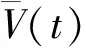
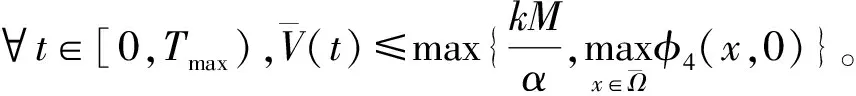
2 平衡点的稳定性分析

设0=η1<η2<…<ηn<…是在Ω上具有齐次Neumann边界条件的拉普拉斯算子-Δ的特征值，E(ηi)(i=1，2，…)是在C1(Ω)上对应于特征值ηi的特征函数空间。{φij：j=1，2，…，dimE(ηi)}是E(ηi)的标准正交基，X=[C1(Ω)]4，Xij={hφij：h∈R4}，则

其中⊕代表子空间的直和。

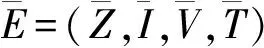
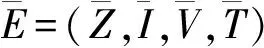
其中Q=diag(0，0，dV，0)，U=(Z，I，V，T)，

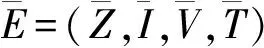
(6)

定理2 若R0<1，则系统(2)—(4)的未感染平衡点E0局部渐近稳定；若R0>1，则E0不稳定。

证明未感染平衡点E0处的特征方程可化为

(7)

显然，ξ1=-m，ξ2=-δ是方程(7)的两个负实根，其余的根由方程

(8)

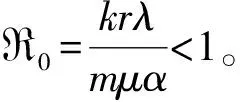
以下只需讨论τ>0的情形。令ξ=iω，ω∈R，代入方程(8)，分离实部和虚部可得

(9)

(10)

将式(9)和式(10)两端平方相加即得

显然，当R0<1时，ω2<0，矛盾。因此，特征方程(8)不存在纯虚根，即当R0<1时，对任意的τ>0，未感染平衡点E0局部渐近稳定。综上，当R0<1时，对任意的τ≥0，未感染平衡点E0局部渐近稳定。

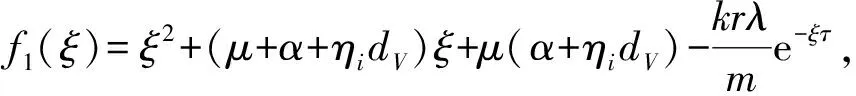
定理3 若R0<1，则系统(2)—(4)的未感染平衡点E0全局渐近稳定。

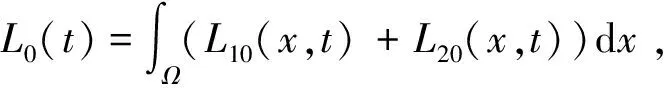
则

于是，

定理4 若R1≤1

则

于是

定理5 若R1>1，则系统(2)—(4)的感染免疫平衡点E2全局渐近稳定。

则

于是