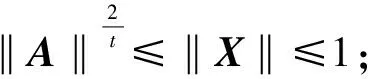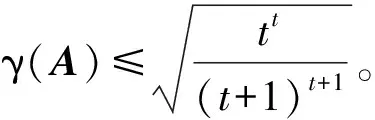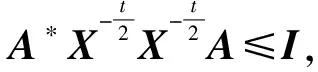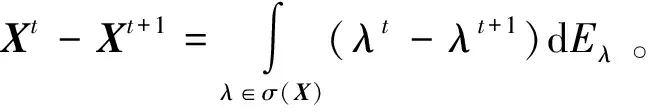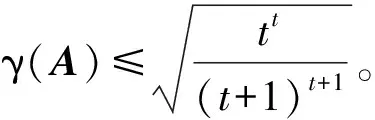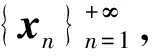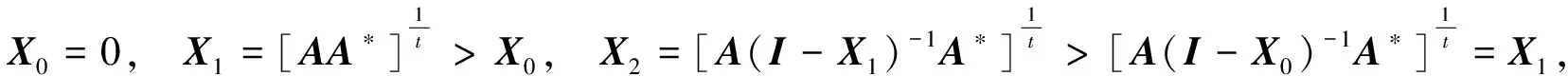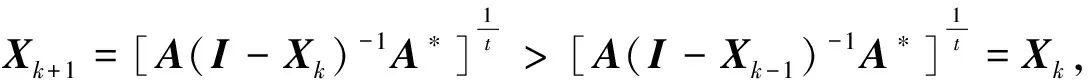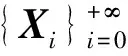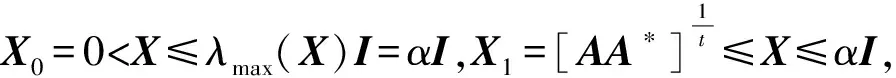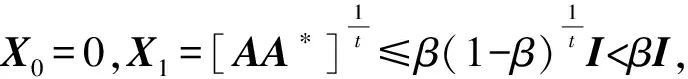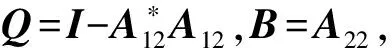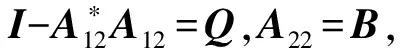算子方程X+A*X-tA=I的正算子解的刻画

杨凯凡

(陕西理工大学 数学与计算机科学学院, 陕西 汉中 723000)

算子理论是泛函分析的重要组成部分，算子方程是算子理论中一个非常重要的的分支，其在动态规划[1]、控制论[2]、随机滤波[3]等方面都有广泛的应用。近年来,在有限维空间上，X+A*X-2A=Q,X-A*X-tA=I等形式的矩阵方程受到许多学者的关注[4-9]。前人主要是在有限维空间上，利用矩阵论的相关知识，给出这类方程有正定矩阵解的一些条件。 本文利用算子理论知识，在无限维Hlibert空间上， 研究方程X+A*X-tA=I正算子解问题，给出此类方程有正算子解的一些充分条件和必要条件。

设B(H)表示无限维Hilbert空间H上的有界线性算子组成的全体。对于A∈B(H), 如果对任意x∈H,都有〈Ax,x〉≥0,则称A为正算子,记为A≥0。对于A,B∈B(H),A≥B表示A-B为正算子。P>0 表示P是正可逆算子,对于A∈B(H)，A*、‖A‖、σ(A)、γ(A)、N(A)分别表示算子A的伴随算子、范数、谱、谱半径及核空间。本文研究非线性算子方程

X-A*X-tA=I

(1)

的正算子解问题，其中A∈B(H)是给定算子，t是(0,1)上的实数。

1 预备知识

引理1.1[10]设A、B是B(H)上的自伴算子且A≤B, 则对任意T∈B(H)有T*AT≤T*BT。

定理1.2[10]设P、Q是正算子,且P≥Q，如果PQ=QP，则对任意实数t>1，有Pt≥Qt。

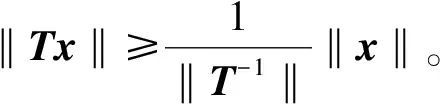
对于B(H)上的正算子，以下事实是显然的：

(1) 对于A∈B(H)有A≤‖A‖I；

(2) 设A,B∈B(H)，若A≥B≥0,则‖A‖≥‖B‖；

(3) 若P、Q是正的可逆算子，且P≥Q，则P1≤Q-1；

(4) 对于0

2 主要结论及其证明

定理2.1 若算子方程(1)有正算子解X,则

(2) 由方程(1)可得

即

定理2.2 若X+A*X-tA=I有正算子解X,则‖X‖=1当且仅当A没有正的下界。

证明必要性:

〈Xx,x〉=1-〈A*X-tAx,x〉，

所以〈A*X-tAxn,xn〉→0。

另一方面，

所以Axn→0，因此A没有正的下界。

充分性:

从定理2.1知‖X‖≤1。假设‖X‖<1,则I-X是正可逆的，因此，存在δ>0，对H上的任意单位向量x，有

〈(I-X)x,x〉≥δ‖x‖2，而A*X-tA=I-X，

所以，

即

因此A是下有界的，矛盾，因此‖X‖=1。

定理2.3 设A是可逆算子，方程(1)在(0,I)上有解的充要条件是存在α∈(0,1) 使得对算子序列

(2)

中的所有算子，有Xk≤αI，此时，算子序列(2)收敛于方程(1)的解。

证明充分性:

假设Xk>Xk-1，则

必要性:

因此对算子序列 (2)中的所有算子，有Xk≤αI。

定理2.4 设A是可逆算子，若存在实数β∈(0,1)使得AA*≤βt(1-β)I，则算子方程(1)有正算子解。

推论1 设X是算子方程X+A*X-tA=I的一个正算子解,则

证明若X是算子方程X+A*X-tA=I的一个正算子解,因为

I>X>0,且0<λmin(X)I≤X≤λmax(X)I，

因此

所以

即

证明若X+A*X-tA=I有正算子解X, 由A*X-tA=I-X可知N(A)⊂N(I-X)。相反地,对任意x∈N(I-X),有A*X-tAx=0,因此X-(t/2)Ax=0,所以Ax=0由此可得N(I-X)⊂N(A)。所以在空间分解H=N(A)⊕N(A)⊥下, 算子A和X有如下的算子矩阵形式

由X>0可知Y>0。由方程X+A*X-tA=I有

即

证毕。