具有集群效应的食饵-捕食系统的稳定性和Hopf分支

周 艳， 张存华

(兰州交通大学 数理学院， 甘肃 兰州 730070)

在我们的生活环境中无时无刻不存在着这样的现象，在一定空间范围内的某两个群体的密度(有时也用浓度或者数量来形容，这里统称为密度)，会因为这两个群体的相互作用而时刻变化着，甚至当其中一个群体的密度受到其他一些不可控因素的影响而改变时，另外一个群体的密度也会随着这一群体密度的变化而变化。例如，某生态系统中的牧群与植被，植被被牧群啃食，当植被较多时，由于食物充足使得牧群的密度在短时间内会呈现递增的趋势，但牧群的增多会加快植被被啃食掉的速度，从而植被密度减少，牧群的密度增长又会受到抑制。针对这类两个群体的相互作用关系，此前已有不少学者根据特定的两个群体的相互作用方式以及这两个群体自身的特征建立了相应的数学模型，并对模型产生的丰富动力学进行了研究，包括传染病模型、食饵-捕食模型、化学反应模型、神经网络模型等。

食饵-捕食关系是这类模型中比较典型的研究对象。20世纪40年代，Lotka和Volterra提出了关于两种群间的竞争关系的Lotka-Volterra模型，奠定了种间竞争关系的理论基础。至今已有不少学者对不同类型的食饵-捕食模型进行了相关的动力学研究[1-4]。在多数食饵-捕食关系中，捕食者或者食饵是集群生活的物种，如羊群、鱼群、斑马群等。然而，集群行为在鱼类中十分普遍，在整个生命周期中，鱼类都会表现出阶段性的集群行为，尤其是洄游性鱼类。一般个体小的鱼类极易形成集群，如鳕鱼、鲱鱼、沙丁鱼、幼年的金枪鱼等，这些鱼类的集群行为能够增加安全系数，起到提高捕食率、共同防御敌害、促进繁殖的作用。有趣的是，某些大型捕食鱼也喜欢集群活动，如鲣鱼、成年的金枪鱼等，显然，大型捕食鱼集群比单独行动更能高效地获得食物。

关于具有集群效应的食饵-捕食模型的研究，此前如Yuan等[5]分析了一类捕食者种群具有二次死亡率、猎物种群具有集群效应的食饵-捕食模型，利用多尺度分析建立了相应的振幅方程，以此确定振幅对均匀扰动和非均匀扰动的稳定性。Tang等[6]针对一类带时滞的食饵-捕食模型，以分析其特征方程得到平衡解的稳定性和Hopf分支的存在性，并根据Faria规范型理论和中心流形定理获得了相应的Hopf分支性质方程，Hopf分支的不稳定引起了斑图的出现。Alidousti等[7]所研究的分数阶食饵-捕食模型，以一个食饵群和两个具有群体防御能力的捕食群作为研究对象，采用Monod-Haldance函数来描述捕食者与食饵之间的相互作用，能够通过证明得到解是有界的，并且同样能够通过文献[6]中的方法获得系统平衡解的稳定性以及Hopf分支的存在性。

本文将考虑如下某鱼群的食饵-捕食系统(模型来源于文献[8])

(1)

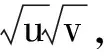
在文献[8]中，通过选取β作为分支参数，Jiang着重分析了对应于系统(1)的具有Neumann边界条件的反应扩散系统

(2)

在其唯一正常数平衡解E*(u*，v*)附近存在的Turing分支。可知，系统(2)中捕食者密度v(x，t)和食饵密度u(x，t)的变化同时与时间变量t和空间变量x有关。而本文将考虑该食饵-捕食模型不含扩散项(即捕食者和食饵的密度变化只与时间变量有关)的情形(1)。同样选取β作为分支参数，进行线性稳定分析和第三焦点值判断，分析系统(1)在唯一正平衡解E*处雅可比矩阵的特征值在复平面的分布情况，获得E*的局部渐近稳定性及Hopf分支的存在性。并且根据第一Lyapunov系数判断Hopf分支的方向及稳定性情况。最后对获得的理论结论进行适当的MATLAB数值验证。

本文的主要结果如下：

定理1 假设0<β<γ<1且令

(3)

则

(1)当β<β0时，系统(1)的唯一正平衡解E*局部渐近稳定；

(2)当β≥β0时，系统(1)的唯一正平衡解E*不稳定；

(3)当β单调递减地穿过β0时，系统(1)在唯一正平衡解E*处经历了超临界的Hopf分支且相应的分支周期解不稳定。

1 正平衡解的稳定性和Hopf分支分析

1.1 正平衡解的稳定性及Hopf分支的存在性

为保证系统(1)正平衡解的存在性，本节总假设β<γ。对系统(1),可知在平衡解处的雅可比矩阵为

容易得到矩阵J的迹T和行列式D的值分别为

由于当β<γ时，行列式D>0，于是可知系统(1)唯一正平衡解E*的稳定性由迹T的符号决定。事实上，由文献[1，9]可知，若T<0，则E*是局部渐近稳定的；若T>0，则E*不稳定。此外，若T=0且相应的横截性条件满足时，系统(1)在E*处可能出现Hopf分支。容易知道，当β<β0时，T<0；当β>β0时，T>0。因此，可初步得到以下结论。

定理2 假设0<β<γ且β0由式(3)给出，则当β<β0时，系统(1)唯一正平衡解E*是局部渐近稳定的；当β>β0时，系统(1)的唯一正平衡解E*不稳定。

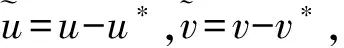
(4)

将系统(4)在其平衡点原点O(0，0)处进行泰勒展开，得到

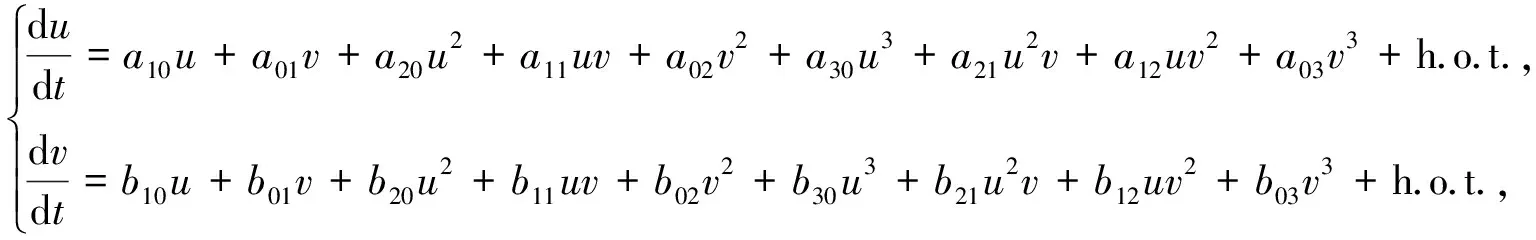
其中

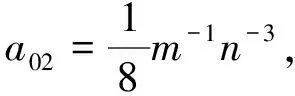
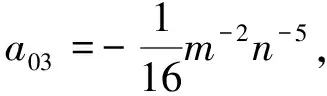
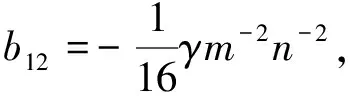
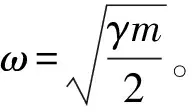
则系统(5)变为

(6)

其中

B30=(b30+b21a+b12a2+b03a3-a30a-a21a2-a12a3-a03a4)b-1=

此时便可以根据第三焦点值的计算方法[10]算得系统(6)在多重焦点(0，0)处的第三焦点值为

当0<γ<1时，α3>0，这说明当β=β0时，E*是系统(1)的不稳定焦点。

此外，注意到当β=β0时，系统(1)在平衡点E*处的雅可比矩阵J的特征方程有一对纯虚特征根λ=±iω。因此，当β在β0附近变化时，矩阵J的特征方程有一对共轭复根λ=ξ(β)±iη(β)，其中

所以

定理3 假设0<β<γ<1且β0由式(3)定义。当β=β0时，系统(1)的唯一正平衡解E*不稳定。此外，当β单调递减地穿过β0时，系统(1)在唯一正平衡解E*处经历Hopf分支。

1.2 Hopf分支的方向及分支周期解的稳定性

根据文献[11]，将系统(6)进一步写为如下形式

其中

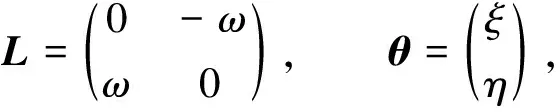
多重线性函数M(θ1，θ2)和N(θ1，θ2，θ3)对向量θ1=(x1，x2)T、θ2=(y1，y2)T及θ3=(z1，z2)T分别取值为

其中U=x2y1z1+x1y2z1+x1y1z2，V=x1y2z2+x2y1z2+x2y2z1。

令

(7)

则q、q*满足

(8)

由式(7)和式(8)可知

所以

g20=〈q*，M(q，q)〉=A20-iA11-A02+iB20+B11-iB02，

因此可求得系统(6)在(0，0)处的第一Lyapunov系数

并且前面求得ξ′(β0)>0，可见系统(6)在平衡解(0，0)处的Hopf分支是超临界的且分支周期解是不稳定的，从而系统(1)在唯一正平衡解E*处的Hopf分支是超临界的且分支周期解是不稳定的。因此有如下结论：

定理4 假设0<β<γ<1且β0由式(3)定义，则当β=β0时，系统(1)在唯一正平衡解E*处的Hopf分支是超临界的且分支周期解是不稳定的。

2 数值模拟

在系统(1)中取γ=0.6，则β0=0.52。

(ⅰ)分别取β=0.2和β=0.4，满足0<β<β0，此时系统(1)的相图见图1，由定理2知系统(1)的正平衡点E*是局部渐近稳定的；

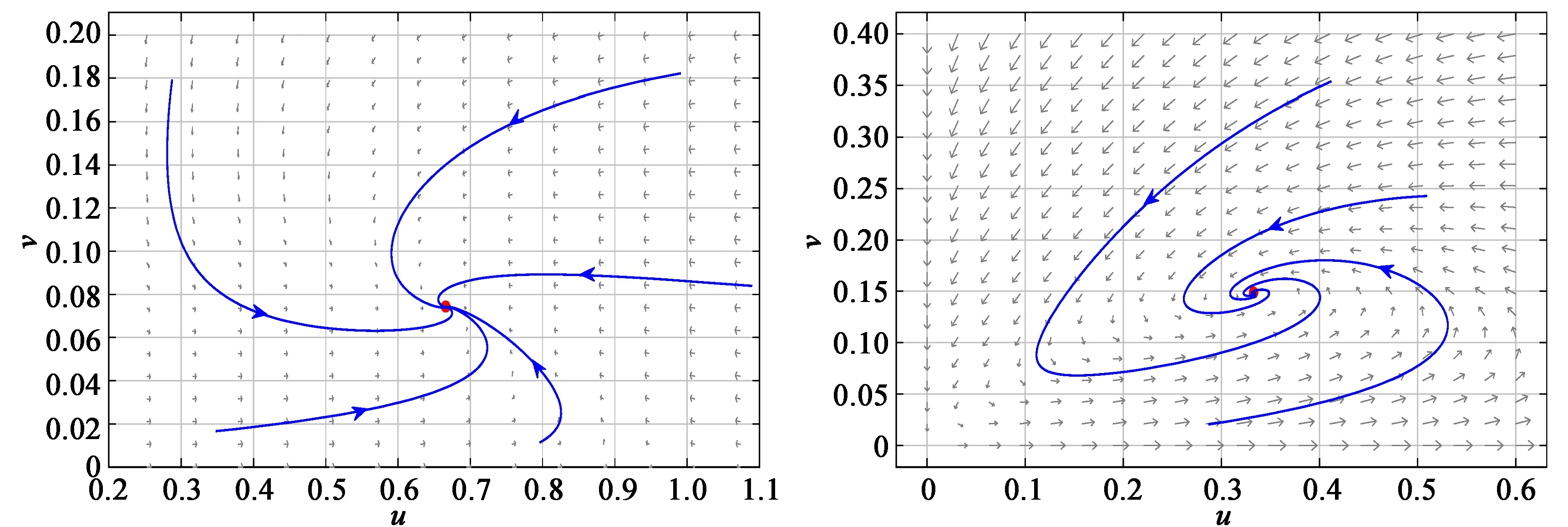
(a) β=0.2 (b) β=0.4图1 平衡点E*局部渐近稳定时系统(1)的相图

(ⅱ)分取β=0.53和β=0.56，满足β0≤β<γ，此时系统(1)的相图见图2，由定理2知系统(1)的正平衡点E*是不稳定的；

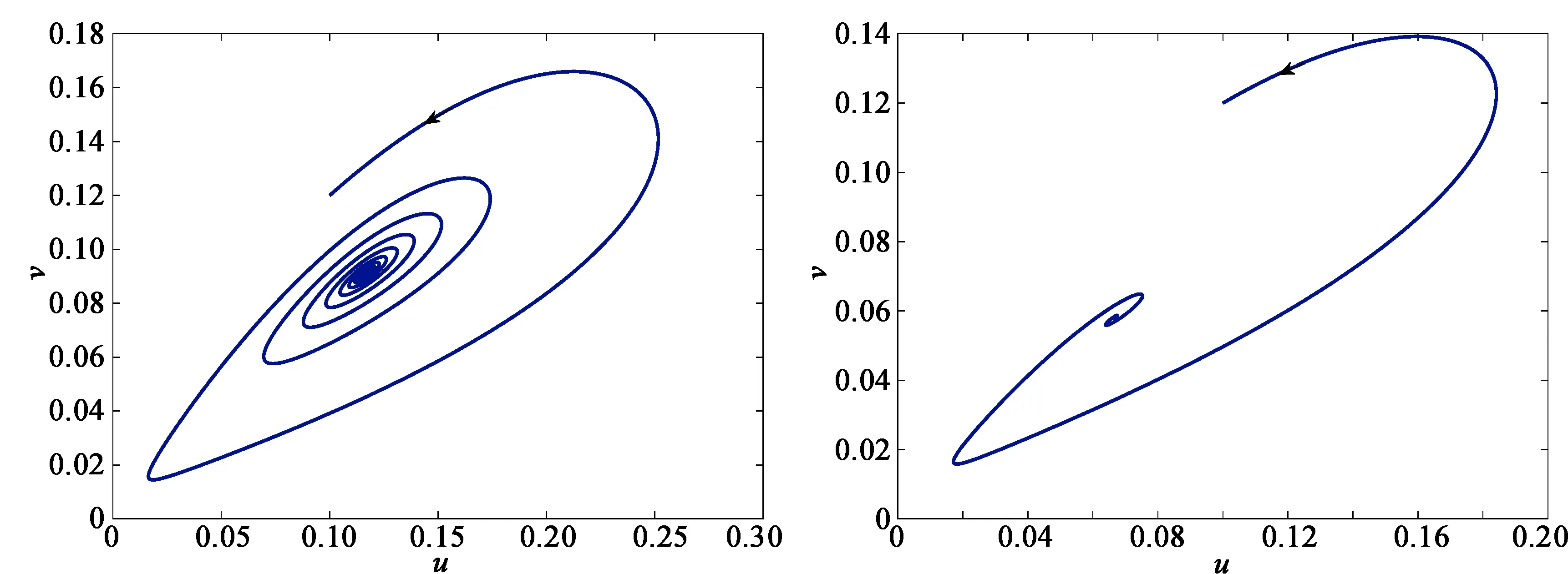
(a) β=0.53 (b) β=0.56图2 平衡点E*不稳定时系统(1)的相图

(ⅲ)取β=0.515，满足0<β0-β≪1，此时系统(1)的相图见图3，由定理3及定理4知系统(1)在唯一正平衡点E*周围存在不稳定的极限环。

(c) 极限环相图图3 β=0.515时系统(1)的相图