基于坝基分层结构的防渗墙渗流场分布
邓佳, 李久江, 李新月, 张钰萌, 张安琪, 赵军, 马会中, 张兰*
(1.郑州大学力学与安全工程学院, 郑州 450001; 2.浙江大学航空航天学院, 杭州 310058)
中国的水利建设工程一直处在大发展时期,各种规格的水利工程对于工农业生产和经济繁荣具有重要意义。其中,渗流问题对工程运行和环境安全都有很大影响。目前中国的堤防工程还有部分未达到国家标准,存在着巨大的安全隐患[1]。作为堤防工程中主要的挡水建筑,其具有堤防型式多、堤防线长的特点[2],其主要遭受渗流变形和渗透破坏。为了实现对混凝土坝基中存在的渗流的控制,主要的措施为防渗和排水。防渗主要是通过延长渗径的方式,从而达到减少出逸压力梯度与渗流量的目的。排水则是为了排除坝基中存在的渗透水,以求降低坝基的出逸压力。提防工程中防渗墙的深度、厚度、渗透系数以及位置等因素发生变化时,坝基的防渗效果均会受到影响。因此要研究和分析堤防工程的安全问题,就必须解决堤坝的渗流问题,提出科学且有效的防渗措施以避免坝基出现渗透现象,同时需对堤防的防渗方案进行优化处理,只有如此才能保障堤防工程的安全运行。陆付民等[1]指出渗透性破坏现象是中国堤防建设工程中较为普遍和常见的一种灾害,应当深入地了解引起渗透破坏的成因,并与各种堤坝进行相关的防渗性加固技术和方案的比较,以便于找到一套既性价比较高且效果显著的加固技术和防渗措施。李曙光[2]就安徽省淮河干流蒙洼蓄洪区堤防工程中的防水防渗、滑坡等工程问题进行探讨,同时分析了造成渗透破坏和边坡失稳的原因所在。马建全等[3]通过渗透-淤堵试验发现通过添加淤堵材料可以有效地提高水力梯度,从而达到降低坝基的渗透系数。而击实淤堵相对于水平铺盖、淤堵和击实等方案兼具防渗与减小投资的效果。柯浩进等[4]利用有限元方法分析了渗透率变异系数对提防渗流场的影响,研究表明水力梯度的标准差会随着变异系数的增大而增大,从而导致局部破坏的概率增大。于舒杰等[5]针对特殊地质条件下的坝基提出了一种基于GeoStudio的防渗处理方法,能够使防渗程度达到90%左右。
以上学者主要针对坝基本身进行防渗研究,而坝基基底的防渗同样不可忽略,因此已有学者针对不同类型的防渗墙及其控制效果进行了研究与分析。刘心岩[6]通过对不同结构形式的防渗墙进行研究,讨论会对其渗流控制效果造成影响的因素,最终提出了不同结构形式防渗墙的设计原则以及应用条件。文献[7-9]建立了不同的防渗墙有限元模型,探讨了模型的稳定性,以渗流计算为基础,得到了垂直防渗方案中防渗墙的适用条件、位置优化以及设计标准。陈晓静等[11]提出封闭渗透系数较大的防渗墙效果更显著,然而防渗墙开裂则会对背水坡一侧造成影响,从而导致边坡失稳。辛欣[12]研究了坝基渗流场随着防渗墙深度增大的变化规律,发现防渗墙的水力比降为先降低后增大。王常明等[13]对防渗墙厚度以及深度进行了优化研究,结果表明在防渗效果方面,厚度变化的影响相对于深度更为显著。另有学者通过数值模拟得到了防渗墙中渗流场的分布特征。张瑜等[14]从Fluent中的多孔介质模型出发,结合有限体积法得到了位于堤防基础中的渗流场分布情况,同时探讨了处于单一防渗措施条件下防渗墙中的渗流场分布。宋永占等[15-16]采用Fluent结合计算流体力学的方法分析流体在坝基多孔介质中的流动规律,得到数值模拟下的各个监测点表征量。同时从理论出发求得渗流场中同一监测点值。通过两者的对比,发现误差是小于3%的,因此能够达到工程所需要的精度。所以,分析复杂流场结构中的可压缩流与不可压缩流时,选用Fluent是完全可行的。
目前对于防渗墙的研究,选取的模型多为单一均质、各向同性的多孔介质模型,而实际研究的对象却是非均质、各向异性且具有分层结构,并且研究过程多采用单因素方法,从而导致缺乏缺少系统化的分析。因此,基于以上研究过程中存在的不足,现提出一种防渗墙设计,以便于不同结构的堤基形式选用不同的防渗墙类型。首先选取Fluent中的多孔介质模型并结合有限体积法,再考虑堤坝地基分层的结构,最终用多孔介质模型表示出来。将防渗墙看作多孔介质模型,考虑其参数变化时对整个堤坝工程的影响。考虑当防渗墙的深度参数发生变化时,与坝基分层结构之间的相对关系,找到最优的深度。从深度、厚度、防渗系数、防渗位置对坝底面扬压力和背水侧出口处渗流量的影响全面系统的分析问题,由此,得到一个可以及时采取有效的紧急水位报警措施的防渗加固方案,以期为在工程实践中面对不同工况的除险加固方案提供决策参考。
1 渗流理论基础
1.1 达西定律
法国工程师达西经过渗透性实验,得到了达西定律,即在横截面为A的情况下通过其的渗流量Q与截面积A或者表达式中的水头差(h1-h2)呈正相关,但是与渗透路径L呈负相关,且与渗透系数存在一定关系。计算公式[17-18]为
(1)
式(1)中:Q为通过截面积为A的流量;K为渗透系数;h1、h2分别为上游水头和下游水头;L为渗流路径长度;V为渗流速度;J为水力坡降。
式(1)即达西定律,通过公式可以发现流体在均质多孔介质中的渗透速度与水力坡降或渗透阻力成比例。
1.2 运动方程
运动方程通常选用纳维-斯托克斯方程来研究不可压缩性流体的流动。即
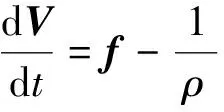
(2)
式(2)中:V为速度矢量;t为时间;f为单位体积流体受到的外力;ρ为流体密度;p为压力;ω为动力黏度与流体密度的比值。
1.3 连续方程
流体渗流的连续方程,即介质可压缩时的质量守恒方程为

(3)
式(3)中:vx、vy、vz分别为x、y、z方向的速度。
1.4 基本微分方程

(4)
式(4)中:kx、ky、kz分别为x、y、z方向的渗透系数;h为水头损失。
各个方向的渗透率恒定,则式(4)化简为

(5)
当介质为各向同性,消去渗透率,即

(6)
2 模型及工况
2.1 几何模型
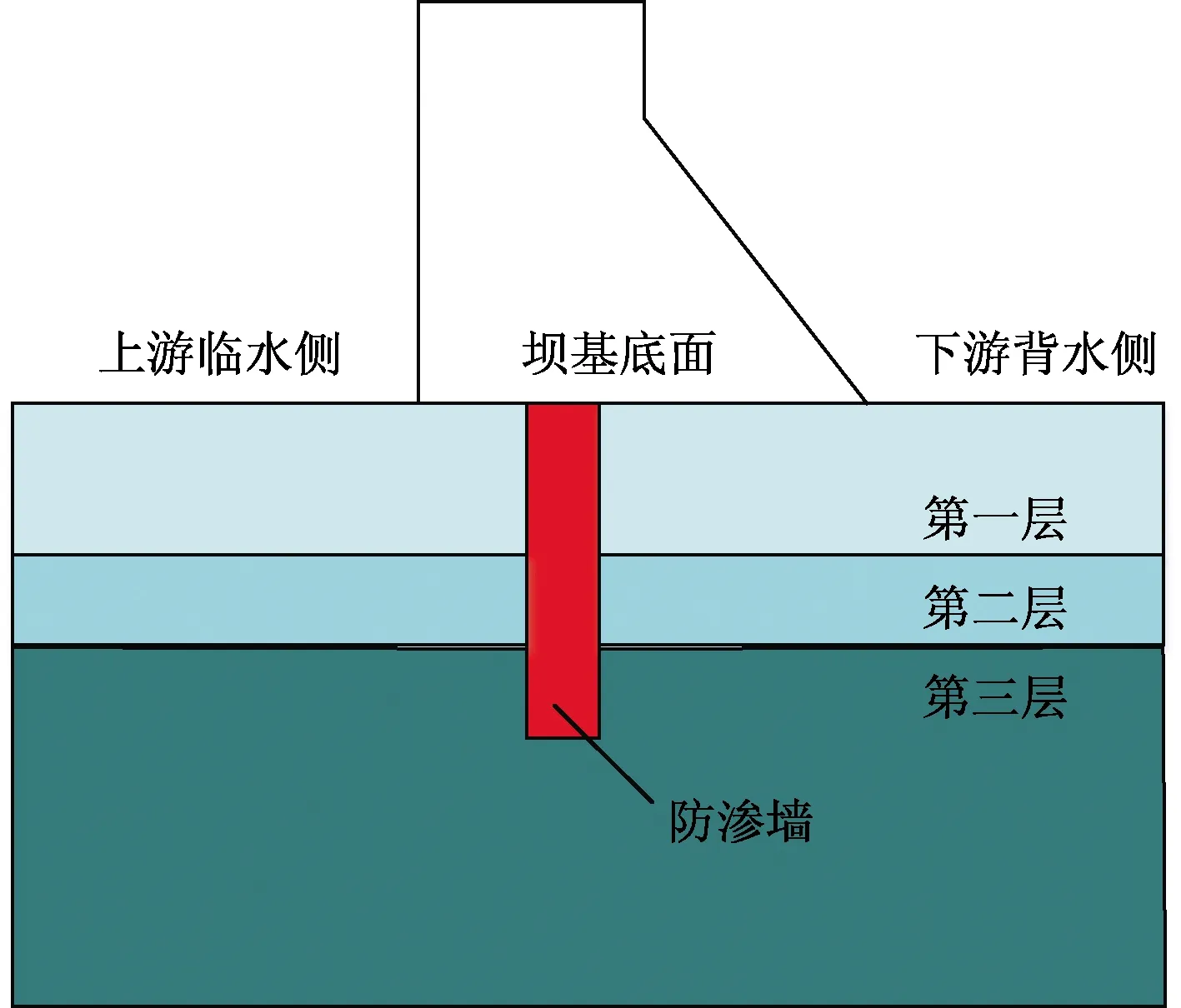
图1 坝基示意图Fig.1 Schematic diagram of dam boundation
取河床中间垂直坝轴线的剖面图为二维流场分析区域,如图1所示,计算区域长度为坝建基面60 m,坝前后水深各80 m。因为简化坝基为二维模型,所以此处假设防渗墙在河床的横向跨度上的防渗效果一样。坝基临水侧的最高水位为100 m,背水侧的最低水位为20 m。假设浅层是以黏土为主的20 m弱透水层,其下是10 m的砂石强透水层,再下层是与浅层渗透系数一致的黏土为主的弱透水层。由于防渗墙的渗透系数比坝基的渗透系数小得多,且考虑到计算速度,所以在研究深度和厚度的单因素影响时,先假设物理模型中的防渗墙完全不透水,边界条件设置为墙。直角坐标系的原点在坝踵位置处,X轴的正向与河流从上游至下游的方向一致,Y轴以向上为正方向。运用ANSYS软件中的Workbench建立几何模型。
2.2 运动方程
初始计算水位为临水侧100 m,背水侧20 m,则进口边界条件为981 000 Pa,出口边界条件为192 000 Pa。其他参数如黏土层的渗透系数、压缩系数1/α、孔隙率的取值分别为1×10-4m/s、1×1013、35%,砂砾层的渗透系数、压缩系数1/α、孔隙率的取值分别2.5×10-4m/s、3.88×1011、50%。防渗墙深度、厚度、渗透系数、位置的变化情况如表1所示。

表1 防渗墙影响因素的变化情况
3 模拟结果分析和讨论
采用Fluent分析不同防渗墙参数下渗流场的总压云图、总速度云图、流线图,计算扬压力和渗流量。引入无防渗墙时的渗流场的渗流量Q和扬压力F,计算不同防渗墙参数下渗流场的渗流量q和扬压力f,通过分析无防渗墙时渗流量和扬压力的比值q/Q、f/F,对防渗墙参数进行优化分析。
3.1 无防渗墙时渗流场模拟计算
首先计算无防渗墙存在时的渗流场的渗流量Q和扬压力F。图2分别为无防渗墙时渗流场的网格划分图、总压云图、总速度云图以及流线图。对无防渗墙时的物理模型计算求得扬压力为4.536 681 4×108MPa,渗流量为0.133 799 kg/s。

图2 无防渗墙时的渗流场分布图Fig.2 Distribution map of seepage field without seepage wall
3.2 有防渗墙时渗流场模拟计算
计算有防渗墙时的渗流场的渗流量q和扬压力f,防渗墙深度为30 m时的网格划分图、总压云图、总速度云图、流线图如图3所示。
当防渗墙深度达到30 m时,防渗墙已经具有较明显的防渗效果。速度最大值发生在渗流绕过第二个直角区且靠近出口处。整个渗流场速度呈均匀分布且速度梯度稍稍减小至趋于稳定。说明此时防渗墙的防渗效果有了明显改善,使流场呈速度分层的稳定渗流。

图3 防渗墙深度30 m时的渗流场分布图Fig.3 Distribution map of seepage field at 30 m of seepage wall
4 封闭式防渗墙的影响因素分析
为了对混凝土堤坝的防渗墙的合理布置提供依据,利用Fluent模拟深度为100 m的半无限深堤基的渗流场,研究了防渗墙的深度、厚度、渗透系数和位置等因素发生变化时对渗流场分布的影响。即是通过单因素变化时的渗流场总压云图、总速度云图和流线图来直观说明渗流场分布的变化,然后通过对混凝土重力坝基面进行计算扬压力大小和对重力坝的出口截面进行计算得到渗流量大小。最后由关系曲线图,判断最合适的参数取值。在最优化的设计方案下,还对变化水位的渗流场分布进行分析,以得到堤坝的储水容量限值。从而通过水位监测判断堤坝的安全状态,及时采取措施来保障堤坝工程的正常运行。
4.1 防渗墙的深度变化对防渗效果的影响
从渗流量和扬压力两个指标进行定量分析,并结合工程成本经济性,选取了深度为30 m的防渗墙。防渗墙深度与渗流量、扬压力的关系曲线图如图4所示,当防渗墙处于30 m时,此时的防渗墙是位于截断强透水层之后的,渗流量和扬压力明显减小。而当深度大于30 m时,防渗效果趋于稳定,曲线的变化趋势变得平缓。如果继续增加深度,会大大增大成本而防渗效果并没有太大的改善。所以,深度为30 m是较为科学的取值。

图4 防渗墙深度与渗流量、扬压力的关系曲线图Fig.4 Effect on the seepage flow rate and the seepage lift pressure of the seepage wall depth
4.2 防渗墙的深度变化对防渗效果的影响

图5 防渗墙厚度与渗流量、扬压力的关系曲线Fig.5 Effect on the seepage flow rate and the seepage lift pressure of the seepage wall thickness
前面已经确定了防渗墙深度,则建立几何模型时墙深为30 m。为了确定最合适的防渗墙厚度,本文从扬压力和渗透量两个方面定量分析,从工程成本经济性考虑。防渗墙厚度与渗流量、扬压力的关系曲线如图5所示。当厚度增加时,f/F和q/Q的变化趋势均为负,说明了厚度增加时渗流量和扬压力是一直减小的。但是,波动的范围并不大。则从防渗墙的厚度来达到理想防渗效果是不现实的,所以防渗墙厚度的确定还是应该以工程成本为主。
4.3 防渗墙的渗透系数对防渗效果的影响
将防渗墙设为和坝基层渗透系数不一样的多孔介质模型,图6为防渗墙渗透系数与防渗效果的关系曲线。

表2 渗透系数和黏性阻力系数设置
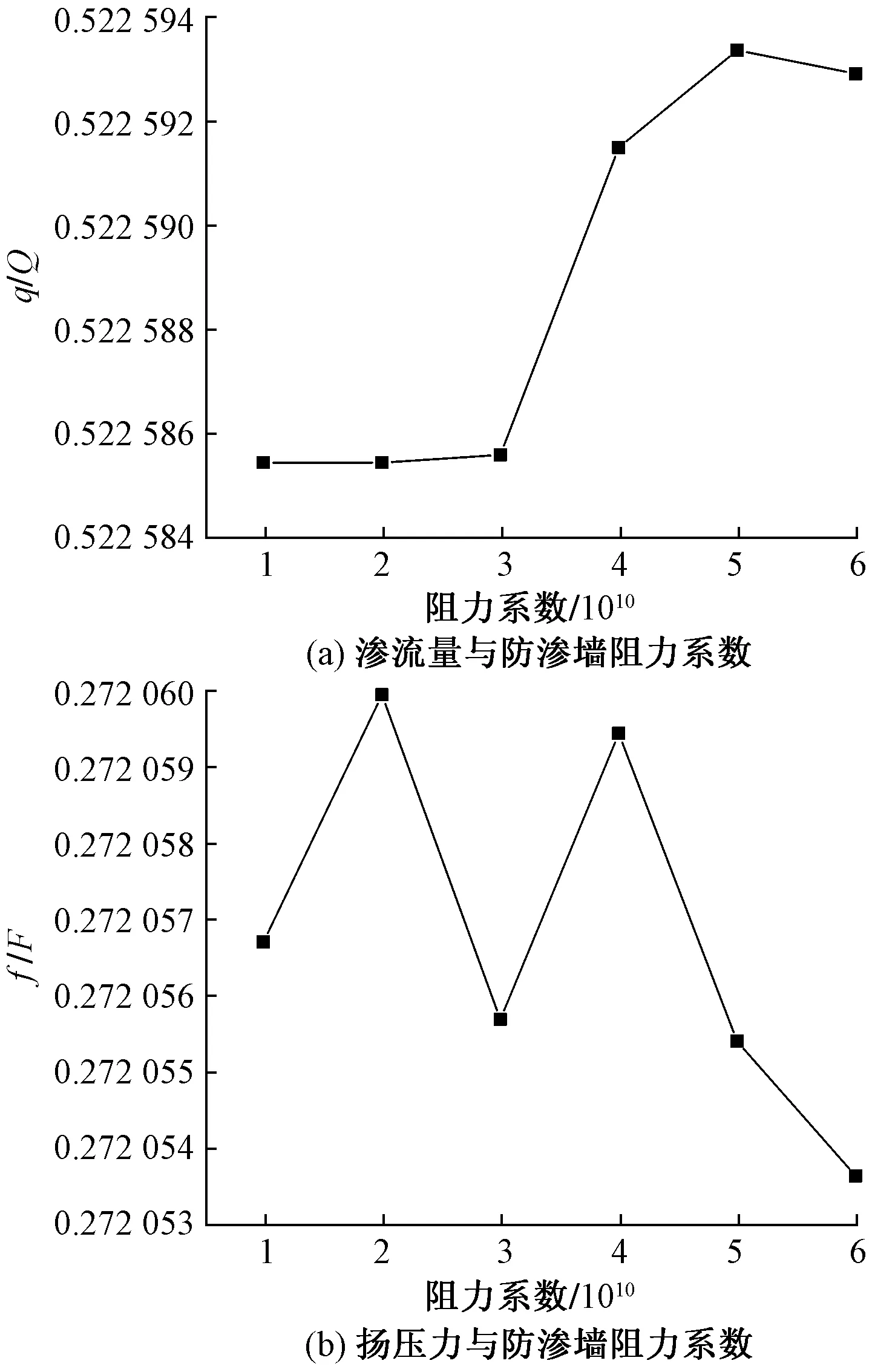
图6 渗流量、扬压力与防渗墙阻力系数的关系曲线图Fig.6 Effect on the seepage flow rate and the seepage lift pressure of the resistance coefficient
线渗流量随着防渗墙阻力系数的增大而不断增大,一直到阻力系数等于9.70×1014即渗透系数为1×10-8cm/s时,渗流量达到最大值。随着阻力系数的增加,扬压力呈现小幅的波动,主要是当阻力系数过小时,渗流场不符合实际情况,所以不做参考。当阻力系数大于9.70×1013时才符合实际条件,不难看出,此时渗流量随着阻力系数的增加逐渐增大到一个最大值,随后呈下降趋势。而扬压力随着阻力系数的增大一直减小。虽然渗流量和扬压力随着渗透系数即阻力系数的变化而变化,但是变化的范围却很小。当阻力系数变化一个数量级时,而成本却相对增加很多。因此,当防渗墙的渗透系数处于工程实际取值范围内,渗流场对其值的变化敏感性较小。通过改变防渗墙的渗透系数来达到较好的防渗效果是不现实且不满足工程经济性要求的。
4.4 防渗墙的位置对防渗效果的影响
图7为渗流量、扬压力与防渗墙位置的关系曲线图,由图7可以看出,渗流量和扬压力都是随着位置增加到一个最大值,而最大值就是发生在防渗墙处于坝基对称轴即位置在27 m处时。因此,防渗墙尽可能地靠近临水侧坝踵的位置时,才能达到最小的渗流量,并且最大限度降低坝基面扬压力。
4.5 堤坝的蓄水水位
图8为渗流量、扬压力与临水侧不同水位的关系曲线,结果表明,临水侧水位的增加,会引起堤坝出口的渗流量和坝基底面的扬压力呈类似近乎线性的增长,即呈均匀增长梯度。且当水位从100~200 m变化的范围中,f/F的值一直小于1,说明坝基面的扬压力在此变化范围中是符合条件的。但是当临水侧水位在180 m时,q/Q的值为1.042 405,说明此时布置了防渗墙的堤坝工程的渗流量超过了无防渗墙时水位100 m时的渗流量。即使此时布置了防渗墙的堤坝工程在外界水位达到180 m时,已经不具备防渗效果了。
所以,从渗流量方面来考虑,可以确定160 m为一级警报水位限,表示应马上采取措施降低水位。而可以设置175 m为二级警报水位限,表示应立即采取措施降低水位,同时采取保护措施以保障堤坝的安全。

图7 渗流量、扬压力与防渗墙位置的关系曲线图Fig.7 Effect on the seepage flow rate and the seepage lift pressure of the seepage wall position

图8 渗流量、扬压力与临水侧不同水位的关系曲线Fig.8 Effect on the seepage flow rate and the seepage lift pressure of the water levels on the water side
5 模拟结果分析和讨论
堤坝工程的安全问题主要是由堤防渗流破坏引起的。所以,堤防的渗流分析对采取科学有效的防渗措施和消除危险状态的紧急措施十分必要。选用Fluent软件中的多孔介质模型结合有限体积法,考虑了堤坝坝基结构分层的情况,对防渗墙的深度、厚度、渗透系数以及位置等参数进行模拟计算。数值模拟结果通过渗流量(扬压力)的关系曲线图来直观反映出来。并以无防渗墙时的渗流场的渗流量和扬压力的值为指标参考值,通过q/Q和f/F来定量表示渗流场的变化情况。得出如下结论。
(1)堤坝坝基因土层的砂石比及粗细比等不同,分为渗透系数不同的结构。结果证明,坝基分层的结构对渗流场的渗流分布有一定影响。特别是,防渗墙方案选择悬挂式防渗墙时(即无防渗墙或防渗墙的深度小于30 m),这时的分层结构是主要影响流线分布的因素。则在工程实际中,应充分考虑坝基的土质分层的情况,确定合适的防渗墙深度。
(2)堤坝渗流场的渗流量、坝基底面的扬压力均与防渗墙深度呈负相关。当防渗墙的深度由25 m增长到30 m,此时防渗墙的底面已由强透水层转变为弱透水层,渗流量和扬压力的减小梯度最大,说明封闭式防渗墙的防渗效果相比于悬挂式防渗墙更为明显。当防渗墙深度大于30 m后,曲线趋势变得平缓,综合工程成本和防渗效果等方面可以确定深度30 m是合理的取值。
(3)根据渗流量、扬压力与防渗墙厚度的关系曲线图,可以得到渗流量和扬压力随着厚度变化虽然值有波动,但是波动差值较小。说明通过改变防渗墙厚度来达到理想的防渗效果是比较困难的。则一般根据实际工程成本来选择厚度是比较科学的。
(4)因为混凝土防渗墙的渗透系数普遍较低,所以可以处理为防渗墙为wall的边界条件。通过模拟发现,防渗墙渗透系数对渗流场的速度和流线分布影响效果轻微,但对渗流场压力分布的影响较为显著。
(5)当防渗墙位置存在差异时,渗流场的压力分布变化明显。同时渗流场的速度梯度和流线也变化较为明显。随着位置数值的增大,渗流量和扬压力也逐渐增大到一个最大值。因此,防渗墙应尽可能地靠近临水侧坝踵,才能以最小改变的渗流量来最大限度降低坝基面扬压力。但同时为了防止防渗墙被拉应力破坏,不建议设置在坝踵即临水侧堤脚处。
(6)当水位变化时,由关系曲线图可知,临水侧水位即进口压力边界条件和渗流量、扬压力是近乎线性的增长关系。但当渗流量或扬压力超过了无防渗墙时的参考指标,就代表此时处于防渗无效的状态。所以可以据此选择出较为科学的参考值作为堤坝的水位警报限。

