变压器直流扰动多物理参数变化特性

徐佳琪， 郭栋*， 卢绍伟， 刘丁华， 高旭宏， 赵越岭

(1.辽宁工业大学电气工程学院， 锦州 121000； 2.北京航天发射技术研究所， 北京 100191)

变压器作为电网中极其重要的设备，其安全稳定运行直接影响电力系统的稳定及安全。截至2019年底，中国特高压线路累积长度3.4万km、累积输送电量1.6万亿kW·h[1]，随着中国特高压线路的建设与使用，由高压直流输电单极大地回路运行侵入交流系统中的直流电流所产生的变压器直流扰动问题常有发生[2-3]。变压器直流扰动状态下励磁电流畸变、铁芯工作点偏移至饱和区域从而导致谐波含量增加、内部构件振动及损耗问题加剧[4-5]。因此，针对变压器直流扰动状态下多物理场参数变化的研究具有重要意义。

针对变压器直流扰动问题，较多学者开展了相关研究，王泽忠等[6]针对直流偏磁状态下变压器温升问题进行仿真及实验，得到构件表面不同位置温升与直流偏磁程度的对应关系。赵小军等[7]采用磁致伸缩测量系统对有无直流偏磁状态下的铁芯磁致伸缩进行量测与分析，并采用频域数值模型，基于谐波平衡法计算不同状态下变压器内部磁场与位移变化。Ahmad等[8]针对直流偏磁状态下变压器绕组及垫块振动特性变化问题，通过电磁场-结构场-流体场耦合的方法，对直流偏磁状态下变压器多物理参数变化进行研究于分析，得到不同直流偏磁状态下绕组构件变形与位移的规律。李明洋等[9]针对直流偏磁状态下变压器的损耗与热点温升问题进行分析，搭建变压器直流偏磁空载试验平台，量测变压器不同直流注入水平下电流、谐波、空载损耗的变化，并总结规律，为大容量电流变压器耐受直流偏磁能力提供参考。

变压器直流扰动状态下励磁电流畸变、振动及损耗问题加剧。目前针对变压器直流扰动状态下的电磁、振动、温升变化已有较多研究，但针对变压器直流偏磁状态下电气、机械、损耗参数的变化原理与多物理场耦合算法未深入研究。与此同时，变压器直流偏磁状态下的仿真分析多针对单一物理场进行，而变压器内部多物理参数的变换存在对应关系，因此，针对变压器直流扰动状态下内部多物理场参数变化规律的研究对变压器耐受直流扰动具有重要意义。

基于此，现针对变压器直流扰动状态下多物理场参数变化问题，研究变压器电磁、铁芯/绕组振动、箱体涡流损耗机理，在此基础上提出变压器多物理场顺序耦合，通过ANSYS及MATLAB联合仿真，分析变压器不同主流扰动状态下绕组电流、励磁电流、绕组/铁芯振动加速度及箱体涡流损耗变化情况。进一步，搭建动模实验平台，采集不同直流扰动状态下电流与振动加速度数据，对比仿真结果，以验证本文算法的有效性及正确性。

1 变压器直流扰动状态多物理场模型

变压器多物理场耦合计算采用顺序耦合方法，以电流密度为电磁场初始激励，电磁场计算结果作为机械-涡流场激励，实现多物理场的顺序耦合。

1.1 磁场模型

假设任意时刻变压器电流激励已知，采用基于磁矢势A的能量平衡有限元法(energy balance finite element method，EBFEM)计算对应时刻的时域电感矩阵，则EBFEM下的磁场模型为

(1)

式(1)中：μ为导体磁导率；B为磁感应强度；J为绕组电流密度；Γ为电流分布情况；V为棱边元体积。

变压器棱边元下的磁场模型可通过Galerkin余量公式求解：

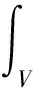
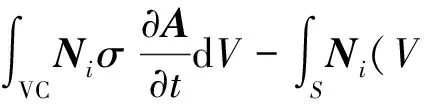
(2)

式(2)中：Ge为Galerkin余量；σ为电荷密度；Ni为矢量权函数；t为时间；S为棱边元面积。

将式(2)进行离散化处理，形成代数方程组，在求解得到磁矢势A的基础上，可进一步求得磁场参数B、H。电磁场计算过程中忽略漏磁及涡流损耗，采用以能量平衡原理计算电磁场参数。

磁场能量增量为

(3)

已知在某一时刻高、低压侧任意两个绕组电流的变化为δiη、δiζ，将激磁电路系统能量增量ΔWc与电感和电流关联，得

(4)

式(4)中：L为时域电感参数；η和ζ定义范围分别为{A、B、C}和{a、b、c}，由电磁能量守恒可联立式(3)和式(4)计算电感。

1.2 电路模型

三相变压器交直流混杂模型如图1所示。

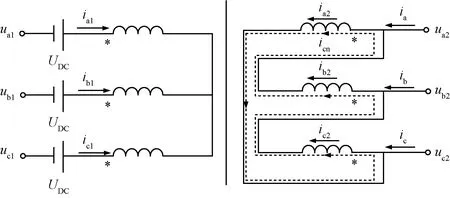
ua1、ub1、uc1和ia1、ib1、ic1分别为Y侧三相线电压和电流参数；ua2、ub2、 uc2和ia2、ib2、ic2分别为Δ侧三线相电压和电流参数；ia、ib、ic为Δ侧 三相绕组电流参数；UDC为直流扰动电压；icn为Δ侧环流图1 三相变压器交直流混杂模型Fig.1 AC-DC hybrid model of 3-phase transformer

忽略励磁电阻及一次侧漏感，变压器回路方程为

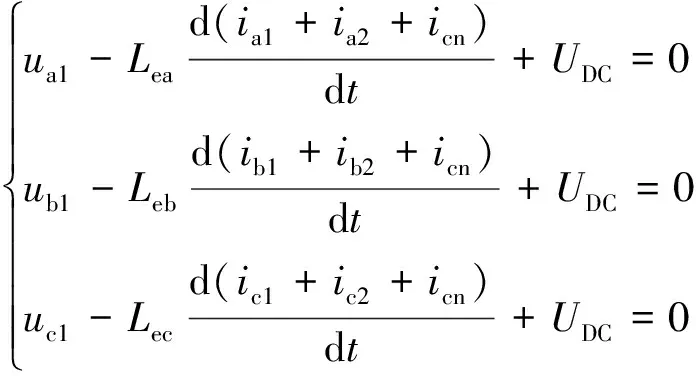
(5)

式(5)中：Lea、Leb、Lec为各相励磁电感。

消去环流icn为

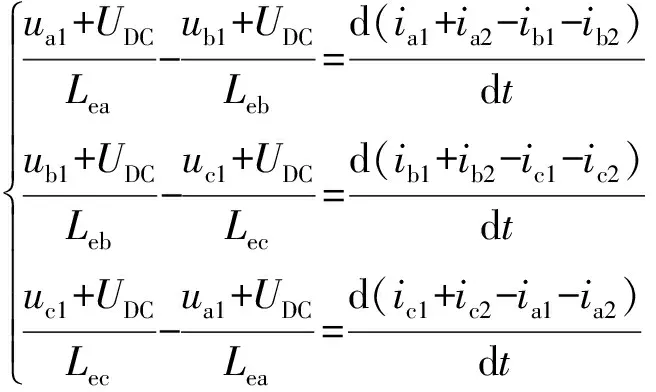
(6)

将Δ侧三相电流进行Δ→Y变换，即

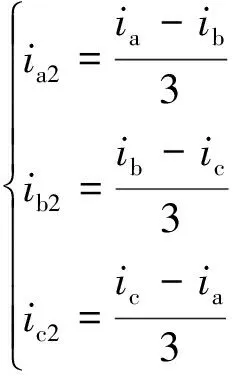
(7)

三相变压器励磁电流计算公式为

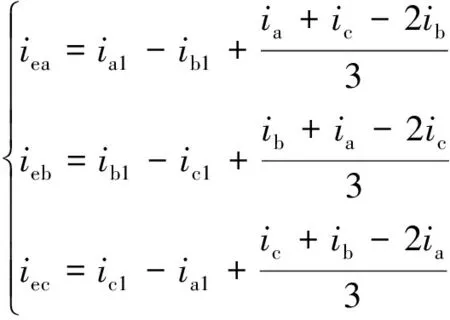
(8)

式(8)中：iea、ieb、iec为各相励磁电流。

1.3 变压器振动模型

变压器振动包括绕组、铁芯及构件振动，其中绕组、铁芯振动为主要振动源。现有研究表明，变压器绕组及铁芯振动分别由安培力及磁致伸缩效应产生并通过流体(变压器油、空气)及构件进行传播，且轴向振动强于径向振动[10-11]，因此，主要针对变压器铁芯及绕组轴向振动进行研究。忽略变压器铁芯夹件及拉板等构件，以变压器铁芯为主要分析对象，研究变压器铁芯振动机理。变压器铁芯振动机理如图2所示。

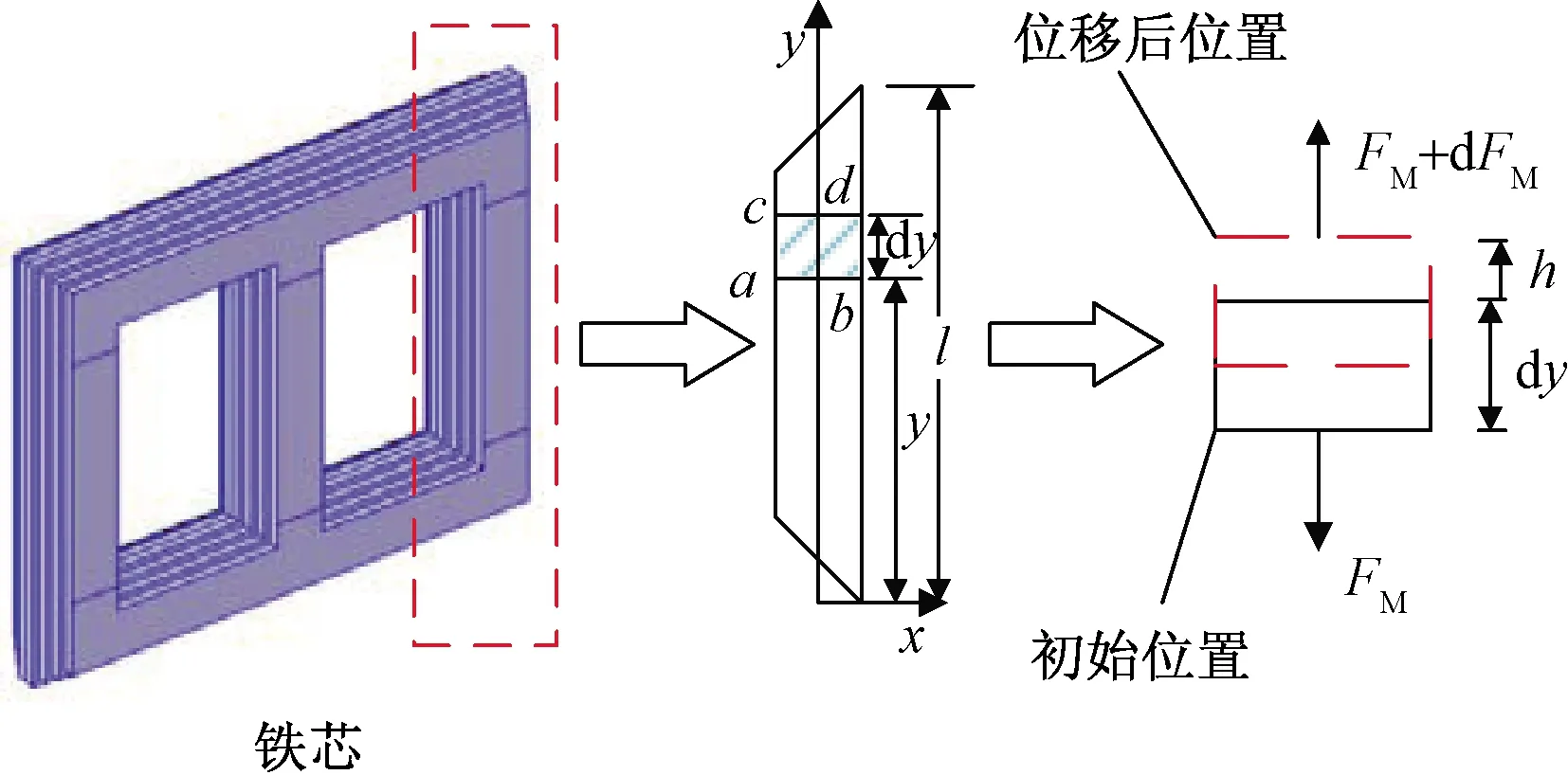
FM为铁芯磁致伸缩力；l为硅钢片长度；a、b、c和d为铁芯单元； x和y为硅钢片分析单元位置图2 铁芯轴向振动机理Fig.2 Axial vibration model of iron core

变压器铁芯为硅钢片堆叠而成，在交变磁场作用下，铁磁材料内部磁畴偏转使得硅钢片单元产生磁致伸缩变形h，磁致伸缩作用下，变压器铁芯产生振动。如图2所示，以硅钢片矩形单元(长度为y)为分析对象，磁致伸缩力dFM作用下，硅钢片单元由初始位置移动到如图2所示位置，随着磁致伸缩力不断改变，使得铁芯整体产生时变振动。

绕组轴向振动激励为通电线圈在磁场中所受安培力，变压器绕组主要包含绝缘(绝缘层、垫块)及线圈两部分，并可分别简化为由受压弹簧k、阻尼c及质量单元m所表示的简化模型(图3)。考虑铁芯及绕组振动模型特性并结合经典动力学原理，变压器铁芯振动方程[11]为

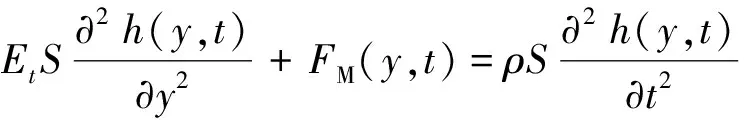
(9)

式(9)中：Et为铁芯硅钢片正杨氏模量；S、ρ分别为铁芯柱横截面积、密度；∂h/∂y、h分别为铁芯单元轴向应变、位移。

kf、ke分别为绕组首末端弹簧系数；cf、ce分别为绕组首末端阻尼系数图3 绕组轴向振动模型Fig.3 Axial vibration mode of winding

绕组轴向振动方程为

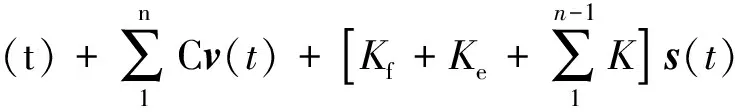
=FA(t)+G

(10)

式(10)中：ar、v、s分别为变压器绕组轴向振动加速度、速度、位移矢量；FA、G分别为变压器绕组安培力及重力；n为绕组匝数。考虑到变压器运行过程中电压、电流激励特性，变压器铁芯振动加速度at及绕组安培力FA分别由式(11)和式(12)计算。

(11)

式(11)中：ε为铁芯单元磁致伸缩率；B为铁芯内部磁通密度；Us为电压激励幅值。

(12)

式(12)中：k为比例系数；Inm为不同频率下的电流激励幅值。

1.4 箱体涡流损耗模型

箱体单元为涡流区，磁场计算方程为

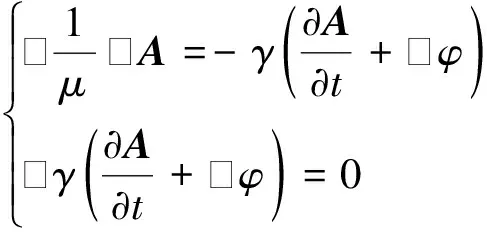
(13)

式(13)中：γ为电导率；φ为标量电位。

对式(13)应用格林定理，得涡流区的伽辽金加权余量方程为

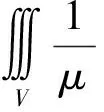
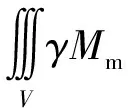
=0

(14)

基于磁场计算结果，获取涡流区单元的电流密度Jt，则箱体的涡流损耗为

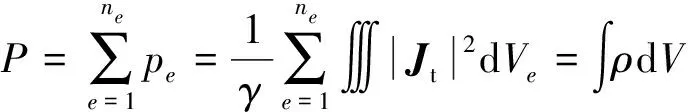
(15)

式(15)中：e为箱体单元编号；ne为单元数；ρ为损耗密度。

1.5 变压器多物理场顺序耦合算法

变压器多物理场顺序耦合算法如图4所示。

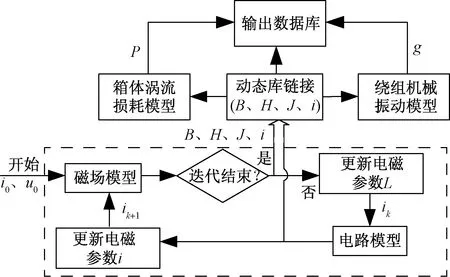
图4 变压器多物理场顺序耦合算法Fig.4 Sequential coupling algorithm of transformer multi physical fields

(1)初始化电压、电流参数作为输入信息，求解电磁模型计算状态变量及其他电磁参数，并将电磁参数作为动态信息库链接振动、涡流损耗模型。

(2)电磁耦合迭代过程中基于电流段及磁矢势进行收敛检查，若绝对收敛范数小于收敛准则值则迭代结束，并将电磁参数输入振动、涡流损耗模型；若迭代未结束，则将状态变量回馈电磁模型，进行下一时刻计算。

(3)以电磁参数作为输入求解振动、涡流损耗模型，计算铁芯及绕组承受的电磁力并输出振动结果，同时计算涡流区损耗，结合电磁参数形成动态信息库。

2 直流扰动多物理场仿真分析

针对一台三相三柱式双绕组干式变压器(SG-1000VA/380V/110V)，依托ANSYS软件建立三维变压器模型，并嵌入编译的控制程序进行多物理场计算。在电磁计算过程中，对变压器绕组施加环形电流密度作为激励，整个变压器施加磁力线平行边界条件，其余为自然边界条件。以α表示直流扰动程度(α为注入直流与空载电流比值)，变压器具体参数如表1所示。有限元模型及振动测点布置如图5所示。

针对空载及75%负载率运行状态下变压器直流扰动状态进行仿真分析，变压器原边接入直流电流源，提供扰动直流，通过设置电流源注入电流，控制变压器直流扰动水平。考虑到变压器原边空载电流与励磁电流基本一致，因此仅针对负载状态下的绕组电流进行仿真。其中负载状态下变压器A相原边绕组电流(iA)仿真结果如图6所示。

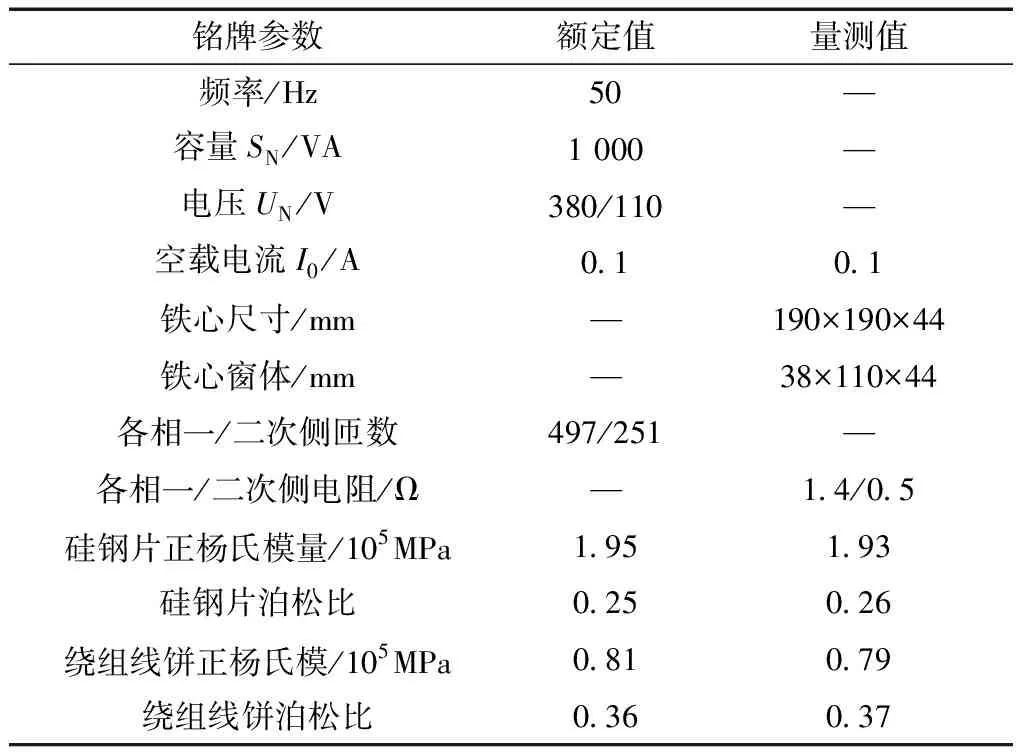
表1 变压器参数Table 1 Transformer parameters

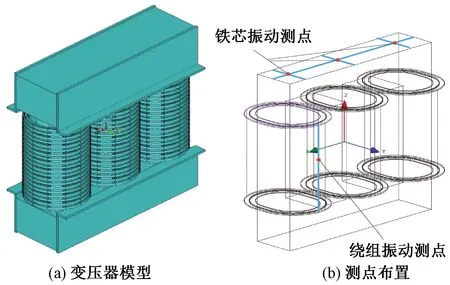
图5 变压器仿真模型Fig.5 Transformer simulation model

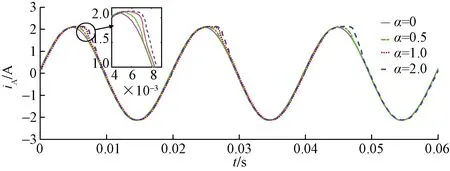
图6 不同直流扰动下的原边电流Fig.6 Primary side current under different DC

不难看出，变压器直流扰动状态下原边电流受到直流影响发生畸变，随着直流扰动水平α的增加，绕组电流畸变程度提高，但电流峰值变化较小。进一步结合图7和图8励磁电流仿真结果分析不同运行状态下变压器励磁电流变化情况。

图7 励磁电流空载仿真结果Fig.7 Simulations of excitation current with no load

图8 励磁电流负载仿真结果Fig.8 Simulations of excitation current with load

由图7和图8可知，变压器未发生直流扰动时励磁电流呈尖顶波，正负半周励磁电流具有对称性。随着直流注入，励磁电流发生畸变，产生半周饱和现象，畸变及半周饱和问题随着直流扰动水平的增加不断提高。空载状态及负载状态下励磁电流变化规律基本一致。

进一步分析不同运行状态下变压器箱体损耗，如图9和图10所示，分别为空载及负载状态下变压器箱体损耗密度分布情况。

结合图9和图10变压器局部模型涡流损耗情况可以看出，变压器涡流损耗主要集中于铁轭及绕组部分，空载运行及负载运行状态下涡流损耗分布规律具有一定的相似性，但负载状态下绕组涡流损耗相比于空载状态下更高，随着直流扰动数值的不断提高，变压器损耗不断提高。

提取如图5(b)所示测点振动数据，将时域振动结果通过快速傅里叶变换(fast Fourier transform, FFT)方法进行时频域转换，得到负载状态下变压器振动加速度仿真结果，如图11所示。

由图11可知，变压器正常运行状态下绕组及铁芯振动加速度主频率为100 Hz，与理论分析一致，但受到铁芯铁磁材料非线性及硅钢片叠制形式影响，铁芯振动加速度FFT结果相比于绕组振动而言复杂度更高(300～600 Hz占比较高)。随着直流扰动的提高，绕组振动加速度变化不明显，铁芯振动加速度幅值及复杂度提高。分析其主要原因，绕组振动加速度与载流体电流密度的二次方呈正比，直流扰动状态下绕组电流变化较小，励磁电流变化明显，因此绕组振动受直流扰动问题影响较小，铁芯振动受绕组影响较大。

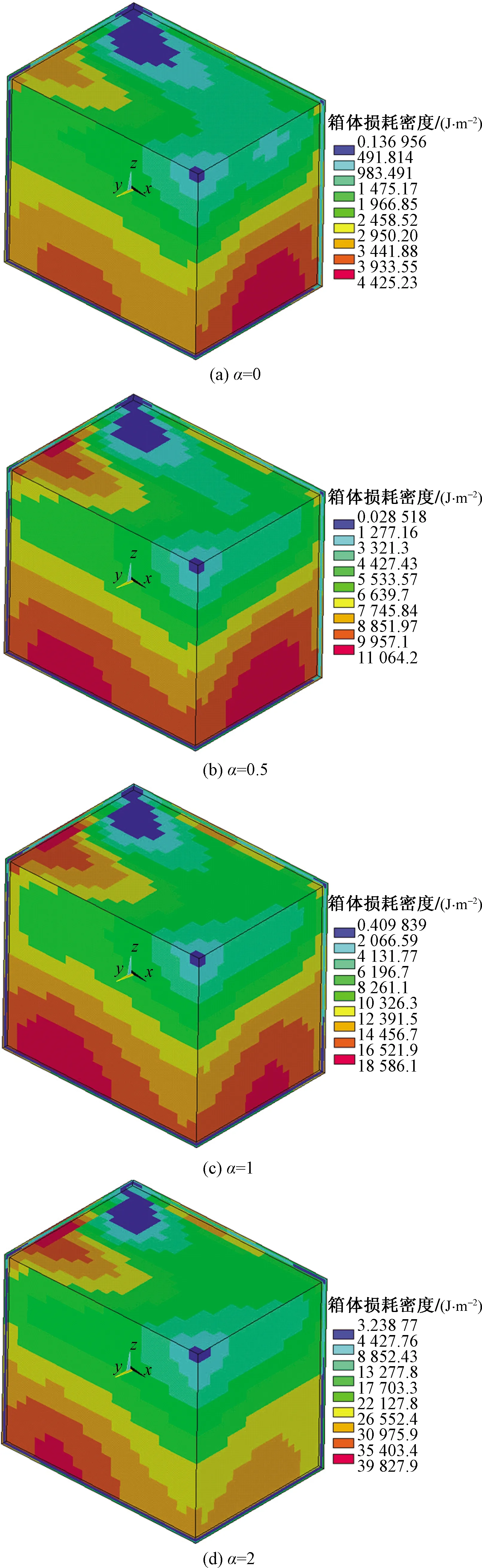
图9 空载运行箱体损耗密度分布Fig.9 Loss density distribution of no load operation box

图10 满载运行箱体损耗仿真结果Fig.10 Simulation of loss at tank with full load

图11 振动加速度仿真结果Fig.11 Simulation results of vibration acceleration

3 变压器直流扰动动模实验

3.1 实验平台搭建

搭建220 V三相变压器直流扰动实验多物理参数采集动模实验平台，考虑到损耗实验数据采集难度，针对变压器直流扰动状态下绕组电流、励磁电流、绕组/铁芯振动加速度数据进行采集。图12所示为实验接线原理图。

R0～R3分别为调压器电阻、变压器原、副边电阻及保护 电路电阻；ZL为可调负载图12 实验原理接线图Fig.12 Principle diagram of experiment

(1)连接实验变压器T2、电流数据采集设备(示波器A1、A2、A3)、调压设备T1、振动数据采集设备、直流注入设备。

(2)设置变压器空载运行，并设置直流注入量，布置振动传感器(磁吸式拾振器)，振动测点与仿真位置一致，进行变压器空载状态下的直流扰动实验，并采集绕组电流。

(3)连接变压器二次侧负载，使变压器处于75%运行状态，监进行变压器负载状态下的直流扰动实验，采集绕组电流、绕组/铁芯振动加速度。

3.2 实验结果分析

图13～图15分别为不同直流扰动状态下的绕组电流、励磁电流实验结果；图16为不同直流扰动状态下振动加速度实验结果。

结合图13～图16不难看出，变压器直流扰动状态下绕组电流产生轻微畸变，励磁电流畸变明显，半周饱和问题严重，铁芯振动加速度峰值变化明显，与仿真规律基本一致。

图13 不同直流扰动下的原边电流Fig.13 Primary side current under different DC

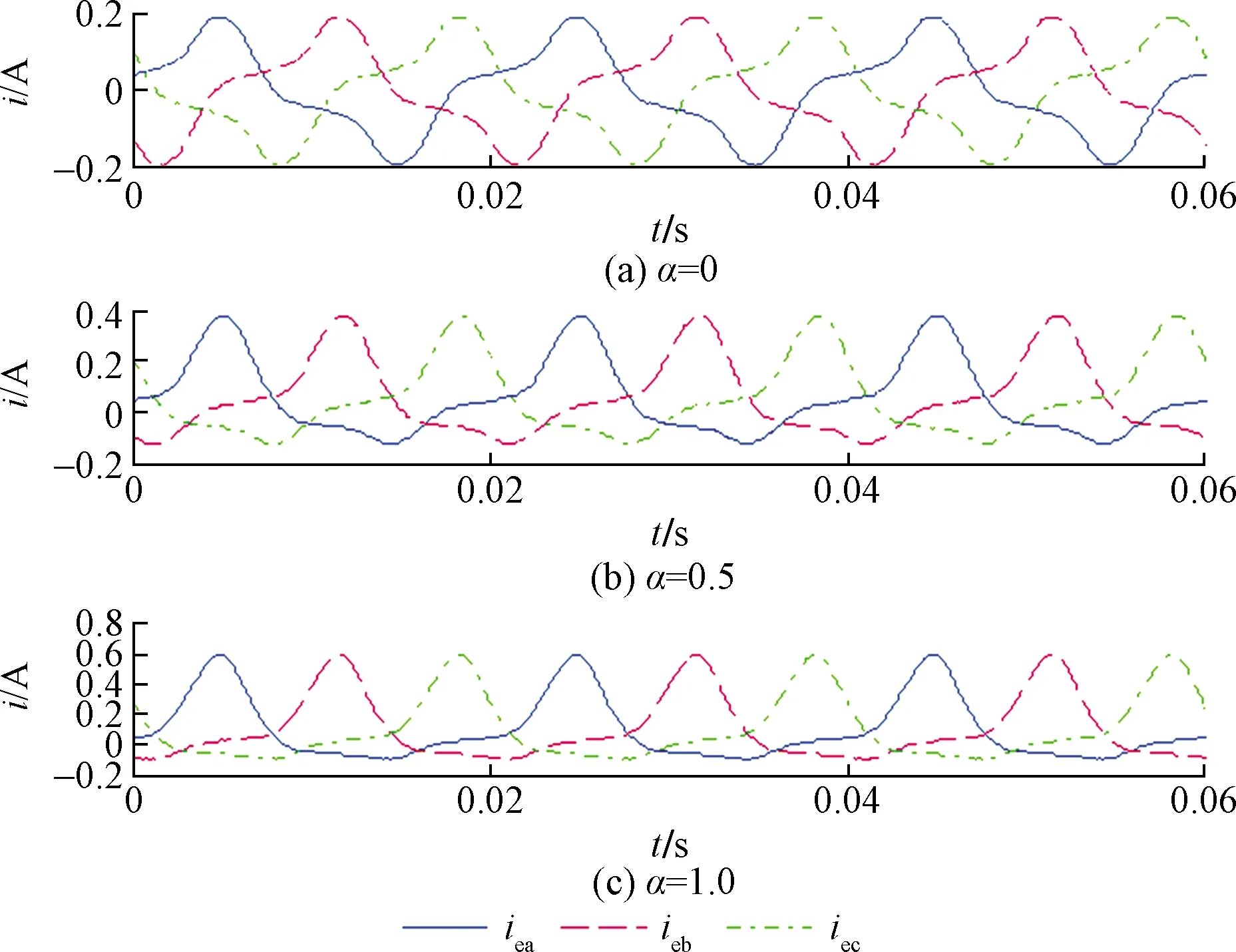
图14 励磁电流空载实验结果Fig.14 Test results of excitation current under no loda

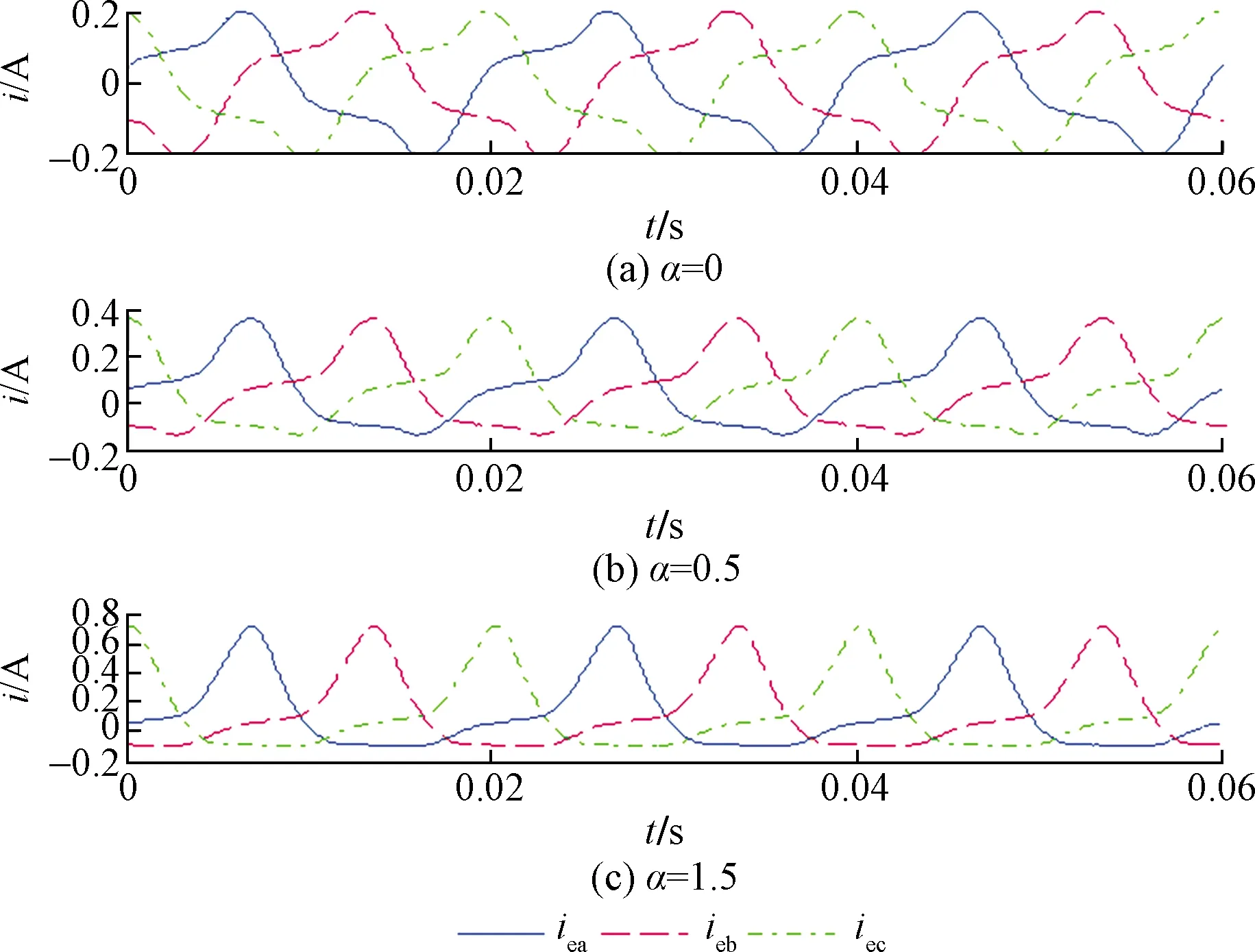
图15 励磁电流负载实验结果Fig.15 Test results of excitation current under loda

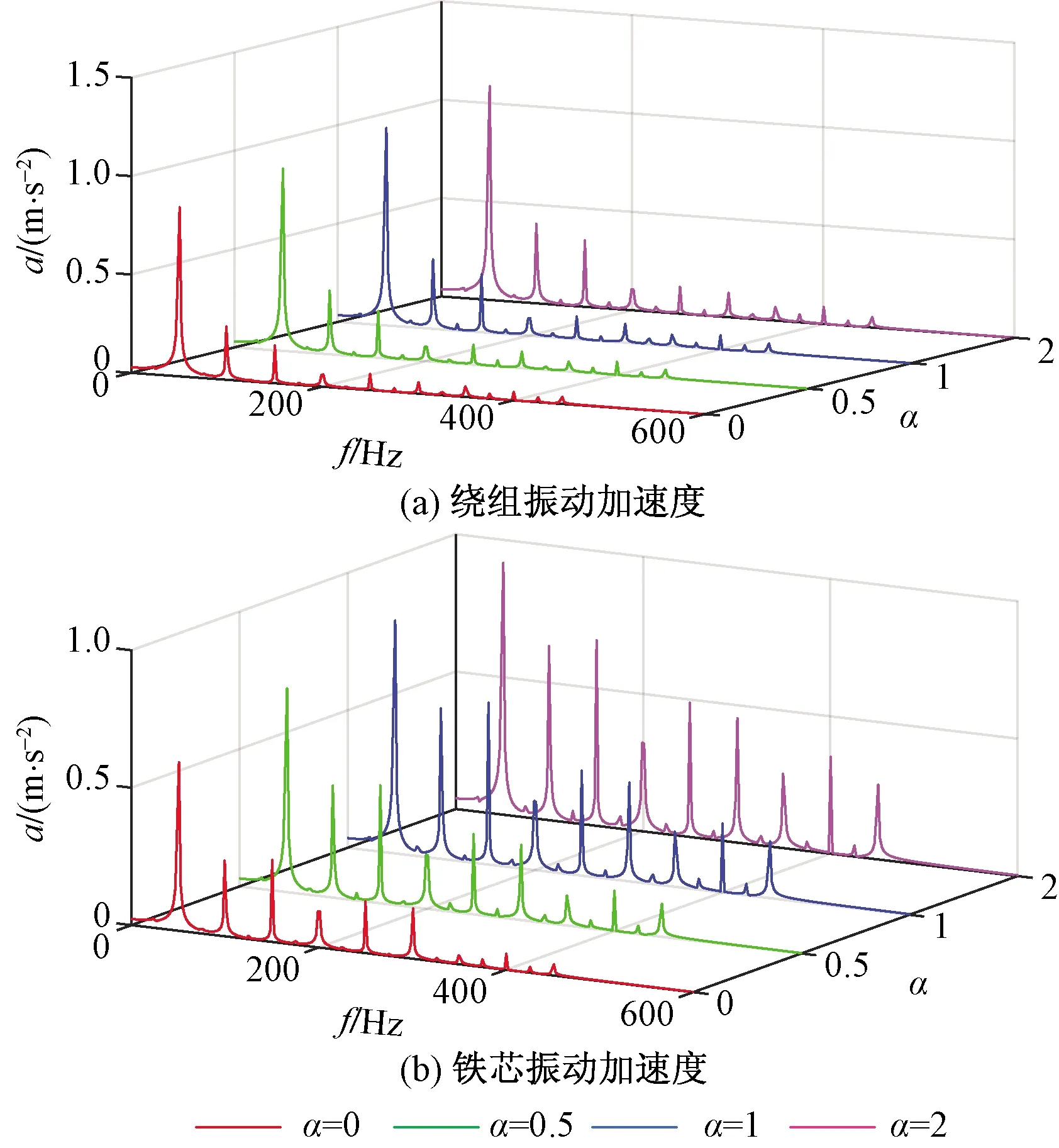
图16 负载运行振动加速度实验结果Fig.16 Experimental results of vibration acceleration under load operation

3.3 误差分析

为进一步验证仿真的正确性，对仿真及实验误差进行分析，如表2和表3所示，分别为变压器直流扰动状态下多物理参数仿真/实验数据对比与误差分析表。结合表2和表3对直流扰动状态下仿真结果误差进行分析，电磁参数误差相较于机械参数误差更小，分析其主要原因，振动信号采集过程中受到环境及实验设备的影响，使得机械参数仿真及实验误差高于电磁参数误差，但仿真及实验多物理参数误差均小于10%，表明仿真结果的正确性。

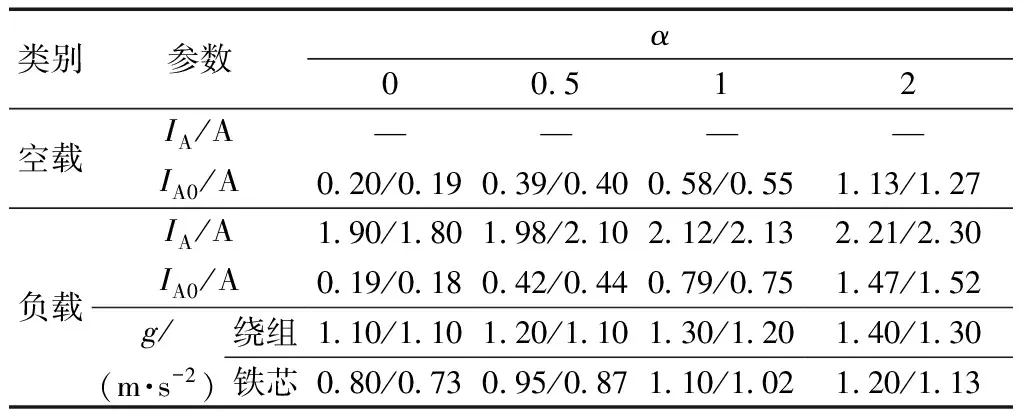
表2 多物理参数仿真/实验数据对比表Table 3 Comparison of simulation/experiment data for multiple physical parameters

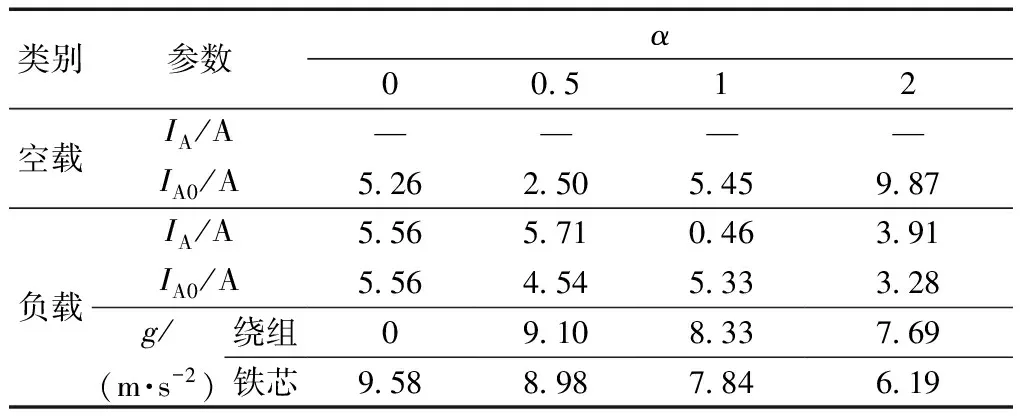
表3 多物理参数仿真/实验误差分析表Table 3 Multi-physical parameter simulation/experiment error analysis table

4 结论

研究变压器直流扰动时多物理参数变化情况，得出以下结论。

(1)基于多物理场顺序耦合算法建立三相三柱变压器直流扰动模型，该模型能够有效计算变压器直流扰动状态下绕组电流、励磁电流、振动加速度及箱体涡流损耗变化情况。通过对比仿真结果和实验数据，验证了该模型的正确性。

(2)变压器直流扰动状态下，绕组电流及振动加速度变化较小，但励磁电流畸变严重、铁芯振动加速度变化明显，变压器损耗升高。随着直流扰动系数α的升高，上述变化情况进一步加剧。

(3)变压器直流扰动状态下，绕组电流变化较小，传统的变压器运行状态监测方案难以有效发现直流扰动问题，但直流扰动状态下铁芯饱和加剧、振动及损耗问题严重，危害变压器的安全稳定运行。