基于蒙特卡罗的光栅衍射条纹强度仿真预测

窦群

(陕西中医药大学医学技术学院， 咸阳 712046)

光栅衍射就是光在传播时躲避障碍物边缘持续传播的过程，是目前了解光学及研究光学相关问题的基础[1-3]。光栅衍射包括单缝衍射和多缝干涉等，会受光栅缝数、入射波长、单缝宽度、光栅常数等因素影响。光栅衍射谱线特征变化多样，包括主极大、次级大形成，主极大缺级、条纹越级、条纹强度变化现象等[4]。

蒙特卡罗方法就是通过随机模拟或统计试验求解数学、物理等问题近似解的数学方法。该方法可应用计算机实现随机试验的模拟，对试验过程进行记录，统计结果，使结果近似于问题正确解，并且可通过计算机程序产生更常见的伪随机数替换真正的随机数，大大提升计算速度[5]。MATLAB是一种功能丰富的科学计算软件，其中绝大多数算法均具备自适应能力，且编程简单，功能强大，效率高[6]。

多年来，中外很多学者都开始从事光栅衍射的研究，在20世纪，耶尔米洛夫等就采用红外光谱去进行平面光栅衍射效率的测试，目前已获得一定成效[7]。近年来，中国学者也在积极研究光栅衍射原理及其应用，唐波等[8]根据X射线源对其衍射成像展开研究；单聪淼等[9]利用菲涅耳衍射积分公式和硬边光阑的复高斯函数分解法开展干涉图样条纹间距的研究，均取得一定成果。关于光栅衍射条纹强度预测的研究一直未有较好的研究成果。如单独采用MATLAB仿真研究预测其强度，那么其理论计算的运算量较大、难度较高，计算的结果也并不精确，不能直观地描述物理图像，无法确切了解光栅衍射规律。因此，为更好地结合物理图像和光栅衍射规律，现利用蒙特卡罗方法随机模拟特点，有效模拟光栅衍射图像，并使用MATLAB软件仿真研究光栅衍射条纹主极大、次级大强度分布，通过各参数值的变化分析相应的光栅衍射条纹强度变化情况。结果图像形象生动，更直观展现光栅衍射的物理过程，以期为光栅衍射强度预测分析理论教学提供有效途径。

1 光栅衍射条纹强度预测方法

1.1 光栅衍射原理

依照惠更斯-菲涅耳原理，采用衍射积分方程获取光栅衍射强度分布公式[10]：

(1)

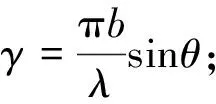
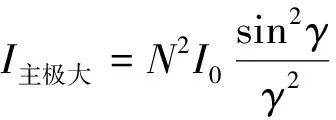
(2)

N缝光栅的两条相近亮纹间暗区存在N-1个暗纹和N-2个亮度微弱的次级亮纹，这类亮度微弱的次级亮纹又称次级大，其强度表达方式为

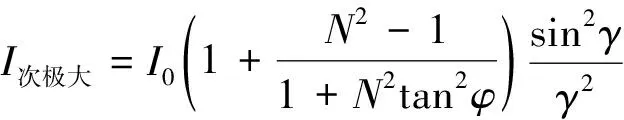
(3)

比较主极大强度和次级大强度，获取次级大相对强度为

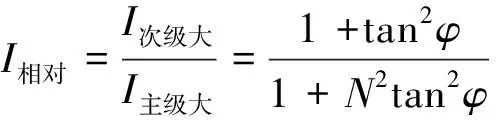
(4)

由式(4)可知，衍射角θ、光栅常数d以及光栅缝数N共3个变量决定光栅衍射次级大强度分布情况[11]。

1.2 蒙特卡罗方法基本原理

蒙特卡罗方法别名随机模拟方法，是利用随机数近似解决问题的一种方法。为解决数学问题，通过搜寻概率统计相似体，经试验取样等一系列步骤，求取该相似体近似解。采用蒙特卡罗方法解决问题得到的解，并非基于经典的数值计算所获取，而是更接近于试验结果。建立随机过程或概率模型，使所求解问题参数等于该问题的解，用近似值的标准误差衡量所求解的精确度[12-13]。

设定目标求解量x表示随机变量ε的数学期望Q(ε)，为近似求解x，通过m次重复抽样随机变量ε，形成彼此独立的随机变量ε序列ε1、ε2、…、εm，并计算其算术平均值：

(5)

蒙特卡罗模拟基本步骤如下。

步骤1明确随机变量ε和随机变量影响变量x两者间函数关系ε=g(x1,x2,…,xn)。

步骤2明确随机函数中影响变量xi的概率密度函数l(xi)、累计概率分布函数L(xi)。

步骤3在(0,1)范围生成随机函数中随机变量xi的若干均匀分布的随机数l(xij)。l(xij)的表达式为

(6)

式(6)中：i为变量个数；j为模拟次数；i=1,2,…,n；j=1,2,…,m。利用式(6)求取l(xij)对应的xij。

步骤4计算统计特征量，代入模拟取得的随机数值到随机函数方程中，得

(7)

(8)

(9)

步骤5绘制随机函数ε直方图，并拟合其分布情况。

1.3 MATLAB仿真研究

利用蒙特卡罗法随机模拟特点，使用MATLAB软件仿真研究光栅衍射条纹强度，通过各参数值变化获得相应衍射光强分布[14]。MATLAB自身携带诸多功能，如产生均匀分布随机数的rand(·)、求和函数sum(·)、绘制直方图函数hist(·)等。此外利用逆概率累计函数可求取已知概率值的概率分布情况[15]。逆概率累计函数应用时调用MATLAB中格式情况如表1所示。

表1 逆概率累计函数调用格式情况

2 仿真算例分析

2.1 光栅衍射条纹主极大强度分析

采用MATLAB计算程序获取光栅缝数N=8光栅衍射条纹强度分布示意图，其中光栅常数φ=5×10-4m，波长λ=6×10-7m，缝宽b=9×10-6m，如图1所示。

图1 光栅衍射条纹强度分布示意图Fig.1 Schematic diagram of grating diffraction fringe intensity distribution

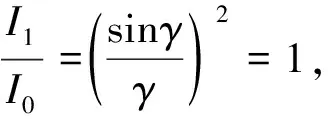
采用MATLAB计算程序获取光栅缝数N分别为8、15、25时的多缝干涉相对衍射条纹强度分布示意图。结果如图2所示。

图2(a)、图2(b)、图2(c)分别描述光栅缝数N=8、N=15、N=25时的多缝干涉相对光强，图2(d)为图2(c)的局部放大结果。对比图1(b)与图2可知，光强与N2成正比，伴随缝数增加，主极大随之增加，光强随之变强。

通过上述仿真结果发现，光栅衍射条纹的主极大强度表示N个单缝衍射强度的包络而非一个。光栅衍射是合并单缝衍射和多缝干涉，其中多缝干涉的主极大强度分布受到单缝衍射主极大调制。光栅衍射主极大强度受N条单缝衍射强度调制。

2.2 光栅衍射条纹的次极大强度分析

假设光栅缝数N=5，波长λ=633 nm，光栅常数d=0.015 mm，缝宽b=0.05 mm，衍射角θ=0°，通过变更光栅常数d、缝宽b和波长λ，观察光栅衍射次级大条纹强度变化情况。

2.2.1 光栅常数对衍射条纹次级大强度影响

光栅常数d分别为0.02、0.04、0.06 mm时，衍射图样变化如图3所示。

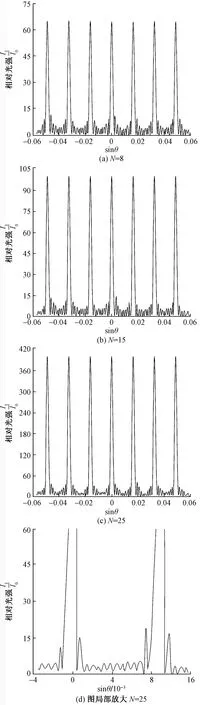
图2 多缝干涉相对衍射光强分布图Fig.2 Relative intensity distribution of multi slit diffraction pattern

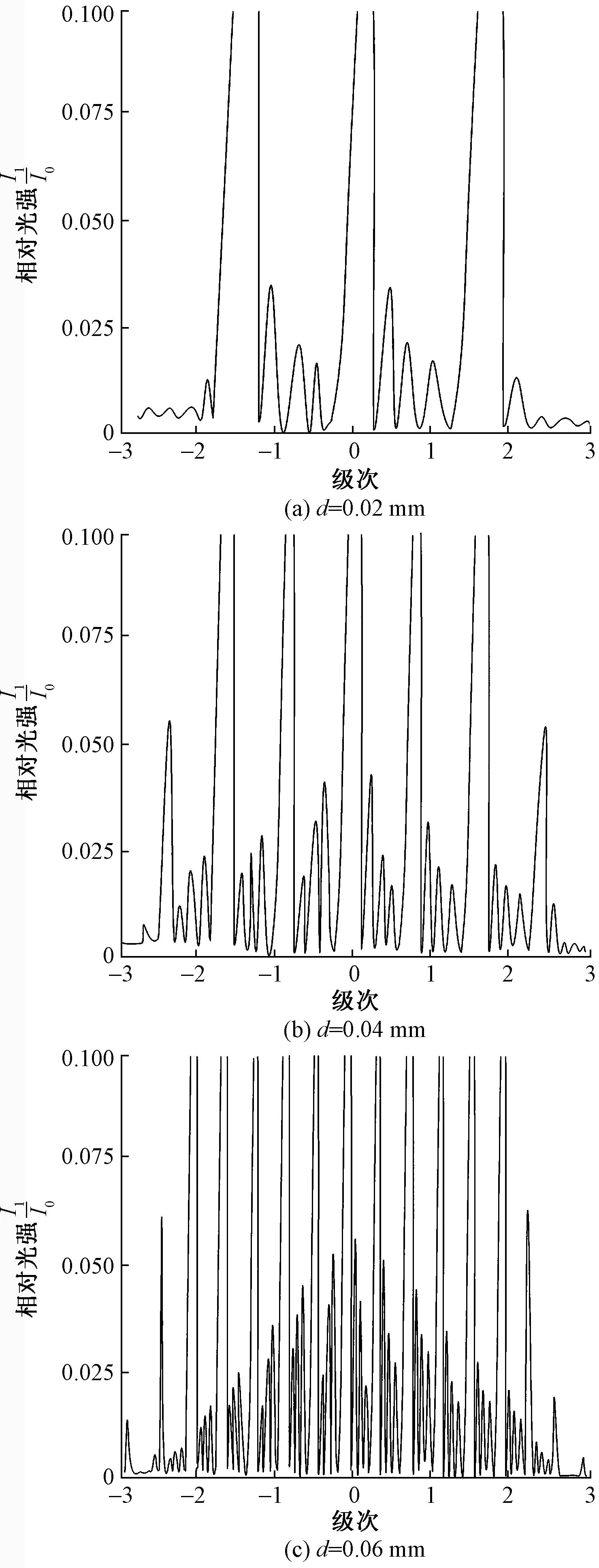
图3 光栅常数对衍射条纹次级大强度影响Fig.3 Effect of grating constant on secondary high intensity of diffraction fringe

分析图3可知，随着光栅常数d的增大，产生的主极大级数随之增加，峰值半宽减小，条纹宽度变窄，处于两个主极大间的次级大个数不变，均为3条，从衍射图样整体来看，条纹次级大强度大小和分布情况大体一致，只是分布密度变大，宽度变窄。

2.2.2 缝宽对衍射条纹次级大强度影响

缝宽b分别为0.001、0.005、0.010 mm时，衍射图样变化如图4所示。

图4 缝宽对衍射条纹次级大强度影响Fig.4 Effect of slit width on secondary intensity of diffraction fringes

图4显示，随着缝宽增大，衍射现象变弱，衍射产生主极大级数变少。

2.2.3 波长对衍射条纹次级大强度影响

图5 波长对衍射条纹次级大强度影响Fig.5 Effect of wavelength on secondary intensity of diffraction fringe

当波长λ分别为λ=335、599、763 nm时，衍射光强分布如图5所示。分析图5可知，波长变大，衍射条纹主极大位置无变化，次级大位置向两侧移动，主极大、次级大半角宽度和条纹间的距离变宽，光栅衍射谱线渐宽，锐度降低。

2.3 实际应用分析

仿真实验测试是在理想的条件下进行测试，得到的结论易与实际实验产生误差，基于此，将其采用实际实验验证实验结果的可靠性。在实验室中，选用分光仪、光栅、水银灯等进行光栅衍射实验，先测定光栅常数和光波波长，再进行其余角度的测试，记录实验数据。实验结果表明本方法可对光栅衍射条纹强度进行精准预测。

3 结论

采用蒙特卡罗方法与MATLAB软件相结合方式，形象、直观地仿真模拟光栅衍射条纹强度变化情况。这种利用计算机完成的仿真实验，不需要复杂的计算，也不需要实验仪器和实验场地便可模拟出不同实验条件下的光栅衍射条纹强度分布和衍射图样，具有较大的应用价值。