基于综合灵敏度的两阶段电压控制分区方法

李英量， 王康， 高兆迪， 蔡鹤鸣， 李飞

(西安石油大学电子工程学院， 西安 710065)

随着电力系统的发展，电网的安全、稳定运行面临着新的挑战[1]。电压控制是复杂电力系统进行电压优化分布、实现系统稳定运行的重要手段[2]。法国电力公司率先提出了分级电压控制，并广泛应用于国内外工程实际[3]。该模式通过二级电压控制，使无功源对所在区域的负荷节点电压控制，实现了系统的电压控制分区。

电压控制分区的目的是将复杂网络划分为若干个具有电压稳定特征的控制区域[4]。目前，中外学者采用现代启发式算法[5-6]、聚类法[7-8]、图论法[9-10]和复杂网络理论[11-12]等方法应用于电压分区问题，解决了复杂系统区域电压控制的难题。为了进一步满足实际电力系统电压控制的要求，文献[13]采用了一种等效传输阻抗法对电气距离进行新的定义，并应用电压分区中。文献[14]利用短路阻抗距离实现了负荷映射分区，保证了无功源的就近归并。

对于研究分区模型以及发电机节点的归并问题方面，文献[15]引入了无功源控制空间，在负荷分区基础上将发电机节点逐次归并，实现全网分区。文献[16]基于节点间耦合关系，给出了电源节点间对负荷节点的灵敏度，依据节点耦合关系的识别，通过递归切割的方式将电网划分为若干分区。上述文献考虑了无功源节点的归并方法与分区模型的建立，解决了计算速度慢、归并困难的问题，但是在考虑功率电压耦合关系、减小无功源归并对负荷灵敏度影响的问题上还存在不足。因此，针对上述问题，现提出一种基于综合灵敏度的两阶段电压控制分区方法。新方法采用的综合灵敏度全面考虑了功率与电压的耦合关系，并基于两步归并法实现了发电机节点的合理归并。

通过考虑无功电压的主要控制作用和有功对电压的弱耦合关系构建综合灵敏度模型，在负荷节点聚合的基础上选取主导节点，采用基于电压稳定性的无功功率-节点电压曲线法和灵敏度法对发电机节点进行两步归并。综合灵敏度模型能够反映系统有功出力对分区过程的影响，更准确地体现电气工程实际；发电机节点的两步归并过程，减轻单纯利用节点类型转化方法进行发电机归并对负荷区域灵敏度的影响。通过算例分析，验证新方法的有效性，该方法能够为电网划分提供新的研究思路，并为局部电压的稳定控制提供理论基础。

1 负荷分区与主导节点选择

1.1 分区模型

1.1.1 综合灵敏度矩阵

节点功率方程为

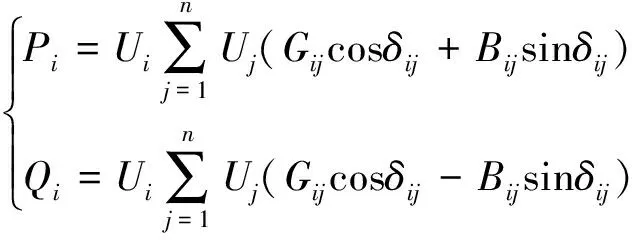
(1)

式(1)中：Pi为节点i注入的有功功率；Qi为节点i注入的无功功率；Ui为节点i的电压；Uj为节点i的电压；δij为节点i与节点j的相角差；cosδij为节点i与节点j的相角差的余弦值；sinδij为节点i与节点j的相角差的正弦值；Gij为节点导纳矩阵的第i行第j列的实数部分；Bij为节点导纳矩阵的第i行第j列的虚数部分； 有功注入Pi、无功注入Qi的功率变化量ΔPi、ΔQi表达到线性方程组为

(2)

式(3)以极坐标下的牛拉法潮流计算，得到构建灵敏度矩阵所需的雅可比矩阵为

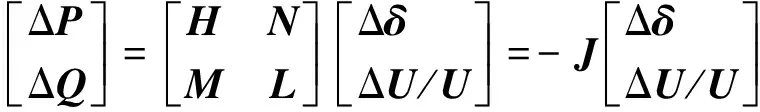
(3)

式(3)中：ΔP为第i节点的有功功率不平衡量；ΔQ为第i节点的无功功率不平衡量；功率变化量由雅可比矩阵J和节点电压的相差ΔU/U、幅差Δδ计算得出，H、N、M、L为雅可比子矩阵，通过雅可比矩阵构建出传统灵敏度矩阵模型为

Svq=-L-1

(4)

式(4)中：Svq为通过雅可比矩阵构建的灵敏度矩阵。

传统灵敏度矩阵的构建是通过对雅可比子矩阵L求逆得到，其物理意义代表无功对电压幅值的强控制作用。构建的灵敏度矩阵不仅考虑了无功功率对电压的主要控制作用，在此基础上还综合考虑了有功功率对电压相差的弱耦合作用。

矩阵N为(n-1)×m阶矩阵，包含负荷节点与无功源节点的有功偏导元素；为保证负荷节点分区准确性，不考虑无功源维度，仅考虑N矩阵含有负荷节点维度的m×m阶矩阵N′m×m：

(5)

含有功-电压接灵敏度矩阵为

Svq=-(L+N′m×m)-1

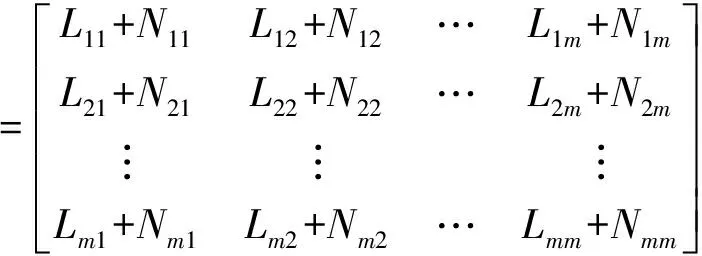
(6)

式(6)中：N矩阵为加入的有功与电压的弱耦合元素；Svq为采用的综合灵敏度矩阵，在不影响无功主控制作用的情况下更切合工程实际。

1.1.2 电气距离矩阵

利用综合灵敏度矩阵Svq推导负荷节点电气距离，由于Svq中无功对电压幅值起主控作用，因此，以节点i、j电压变化量的幅差量化灵敏度矩阵为

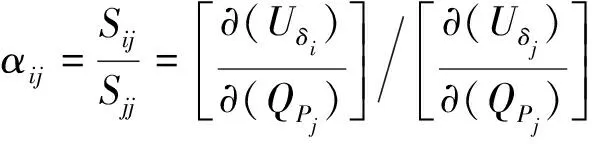
(7)

式(7)中：αij表征节点之间的电压耦合，通过节点之间电压变化的最大衰减来量化；∂(USi)/ ∂(QPi)为综合了无功对电压幅值和有功对电压相差弱耦合作用的新灵敏度模型，与Svq中元素对应。

为了测量对其他节点具有的对称性电压变化，定义距离矩阵元素dij为

dij=-αijαji

(8)

式(8)中通过映射函数，扩大坐标之间的差异性，从而更好地表征距离区分度：

Dij=-lg(αijαji)

(9)

式(9)中：Dij为电气距离。

为了获得直观的节点聚合过程，方便聚合距离计算，需要寻找D0中的最大值Dij=Dmax，其中，i,j=1,2，…,m，并做归一化处理，得到的初始距离矩阵D0，即所求电气距离矩阵。

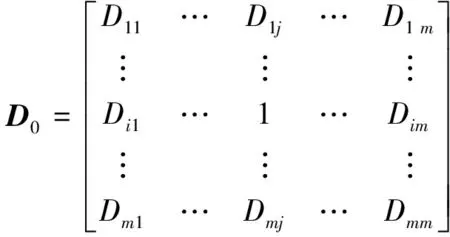
(10)

1.2 负荷分区过程

基于综合灵敏度得到的综合电气距离，利用节点聚合方法得到负荷分区，具体步骤如下。

(1)输入初始电气距离矩阵D0，每一个负荷节点对应一个初始区域。

(2)初始化迭代计数器j=1，定义矩阵D1=D0；

(3)寻找网络中不为零的节点间最小距离，即

Dm,n(j)=minDi,x,i,x=1,2，…,N,Di,x≠0

(11)

式(11)中:Dm,n(j)为在第j个矩阵节点(m,n)之间的电气距离元素值；minDi,x为其中的最小值。

(4)寻到指定元素置零并Dm,n(j)=Dn,m(j)，将行列所对应的节点拟合为新的虚拟节点。

(5)采用最大距离准则重新计算聚合之后的虚拟节点与剩余节点间的距离，若Di,m(j),Di,n(j)≠0，则取两列之间最大数，如式(12)所示；否则Di,m(j)=Di,n(j)=0。

Di,m(j)=Di,n(j)=max[Di,m(j),Di,n(j)]

(12)

式(12)中：Di,m(j)为在第j个矩阵节点(i,m)之间的电气距离元素值；Di,n(j)为在第j个矩阵节点(i,n)之间的电气距离元素值。在进行剩余节点最大距离置换时，选取虚拟节点维度外的最大非零元素，并且不可以置换虚拟节点所在维度的值。

(6)对步骤(5)取对称阵，得到新的分区结果，包含负荷节点聚合后虚拟节点区域与剩余节点。

(7)存储得到的矩阵D(j)并返回步骤(3)，若D(j)是非零矩阵，则j=j+1。

(8)输出电气距离矩阵D(j)，其中，j=1,2，…,N，网络中的分区个数由N逐次减少到1。

(9)在节点虚拟聚合过程中，根据网络拓扑结构与电压控制分区计算原理可以确定标准化电气距离阈值δ。寻找第一个指向j′的数，使得与j′相关联的距离矩阵D(j′)中所有非零元素均大于分区阈值δ。

(10)在所选的D(j′)的每组区域中，元素为0所对应的节点划分为一个区域。

(11)输出所划分区域个数Nz=N-j′+1，包括第h个区域对应节点指针。

1.3 综合灵敏度下的主导节点选择

风电出力会影响接入负荷区域的电压稳定性，为此，可选取负荷区域内的主导节点来增强电源对所在区域的可控性。主导节点的选择是基于区域电压可控性为目的，式(13)代表了可控性目标函数。

maxf=min{∑|Svq(i,n)||i,n∈1，2，…，Zh}

(13)

式(13)中：maxf为选取主导节点的目标函数，其以某节点i的n个灵敏度矩阵元素值Svq(i,n)之和在所在区域h中数值最小为目标；Zh为区域h的节点Z。

节点相互电压控制能力应不同，且主导节点应该反映对其本身的控制能力。文献[17]以初始电气距离作为可控性目标函数求取主导节点。但由于距离矩阵是通过数学映射取的对称，主导节点对自身的距离为零。因此，选取初始电气距离无法反映节点对自身的电压可控性。

针对上述问题，目标函数以“最小-最大”准则求解，综合灵敏度矩阵Svq可以反映主导节点对其本身的电压控制能力，作为主导节点目标选择更精确。主导节点对应区域内节点非零元素和越小，代表电压控制能力越强，进而可以确定主导节点。

2 发电机节点两步归并过程

传统方法经过负荷分区后，再通过经验就近归并发电机节点的过程存在一定的不足。文献[18]基于电压稳定性的Q-V曲线法实现了无功源节点的部分归并，其余节点就近归并，分区结果虽然满足拓扑结构，但可能存在连通性误差。文献[15]采用逐次递归法进行发电机节点的归并，解决了文献[18]中剩余发电机节点的归并问题，但是节点类型的转换会影响负荷节点灵敏度。为了减轻这种影响，提出了一种两步归并的方法归并发电机节点，进而实现全网分区。

2.1 基于电压稳定性的Q-V曲线法

文献[19]指出，网络电压失稳的主要原因是某节点或区域连续的节点组发生无功短缺，而Q-V曲线法[20]正是基于无功容量控制电压稳定性的主要方法，可以直接地确定无功短缺的位置。因此，对比节点的Q-V曲线可以准确定位具有相同电压稳定性的节点，并得到基于电压稳定性下的发电机节点初步归并。

利用连续潮流计算得到负荷节点Q-V曲线，比较所有负荷节点的Q-V曲线，将满足以下极小值点(Vmin,Qvmin)条件的母线划分为一组：①曲线的极小值点近似相同；②在极小值点处达到无功限值的发电机组。Q-V曲线示意图如图1所示。

A0、A1、A2分别为节点0、1、2的极小值点(Vmin,Qvmin)； Qb0、Qb1、Qb2分别为三种节点的无功裕度图1 Q-V特性曲线图Fig.1 Q-V characteristic curve

由上述两个条件可以得到基于电压稳定性的电压控制区域，其中包含部分PV节点的初步归并。

2.2 基于无功源控制空间的发电机归并

根据无功源控制空间的思想，以准稳态灵敏度的概念，将发电机节点逐次的设置为负荷节点，保证了自动电压控制设备的准稳态控制响应特性。

考虑到2.1节中剩余的发电机节点的归并，仅增加未归并发电机节点的灵敏度维度，对负荷节点的灵敏度影响较小。文中采用的灵敏度矩阵模型包含有功和无功对电压相差的弱耦合作用，得到的灵敏度矩阵更符合工程实际。具体归并步骤如下。

(1)通过节点类型的转换，将基态下的调节能力接近临界值的发电机节点按照负荷节点对待，称其为负荷电源节点，并在潮流中转换节点类型。

(2)设系统共n个节点，m个负荷节点，剩余未归并的发电机节点个数为α，需要逐次把α个发电机节点逐次归并为负荷电源节点。

(3)若上一个负荷电源节点的无功未达到上限，则应将其节点类型改回发电机节点。

(4)重复式(6)～式(9)的步骤，可以得到未归并的α个发电机节点对应灵敏度与电气距离矩阵为

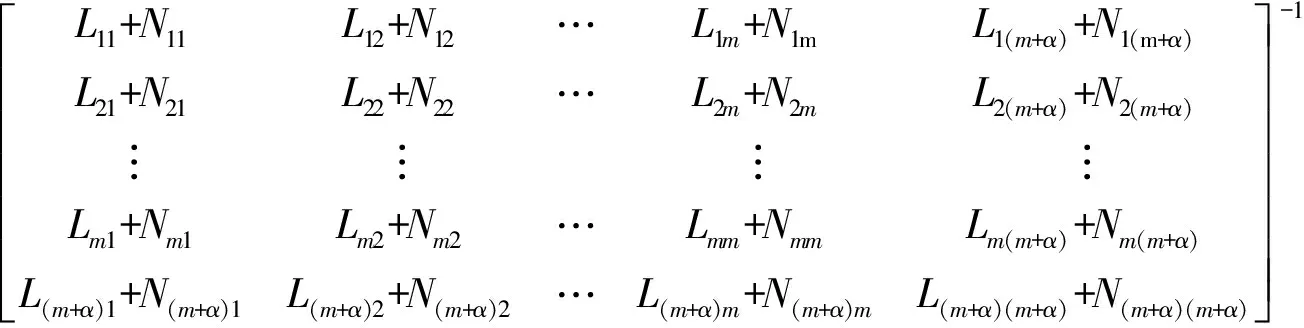
(14)

式(14)中：Svq1为第α个发电机节点转换后的灵敏度矩阵(α∈m+1～n)，通过此灵敏度矩阵得到包含第α个发电机节点转换后的电气距离矩阵D′ij：

(15)

(5)通过灵敏度法进行发电机节点的归并，得到全网分区。在进行完2.1节中初步归并之后，若系统平衡节点仍未归并，进行节点类型转换法时应设置新的平衡节点，保证系统功率平衡稳定。

2.3 流程图

由上述方法计算能够形成最终的电压控制区域(voltage control area,VCA)。

基于综合灵敏度的两阶段电压分区流程如图2所示。

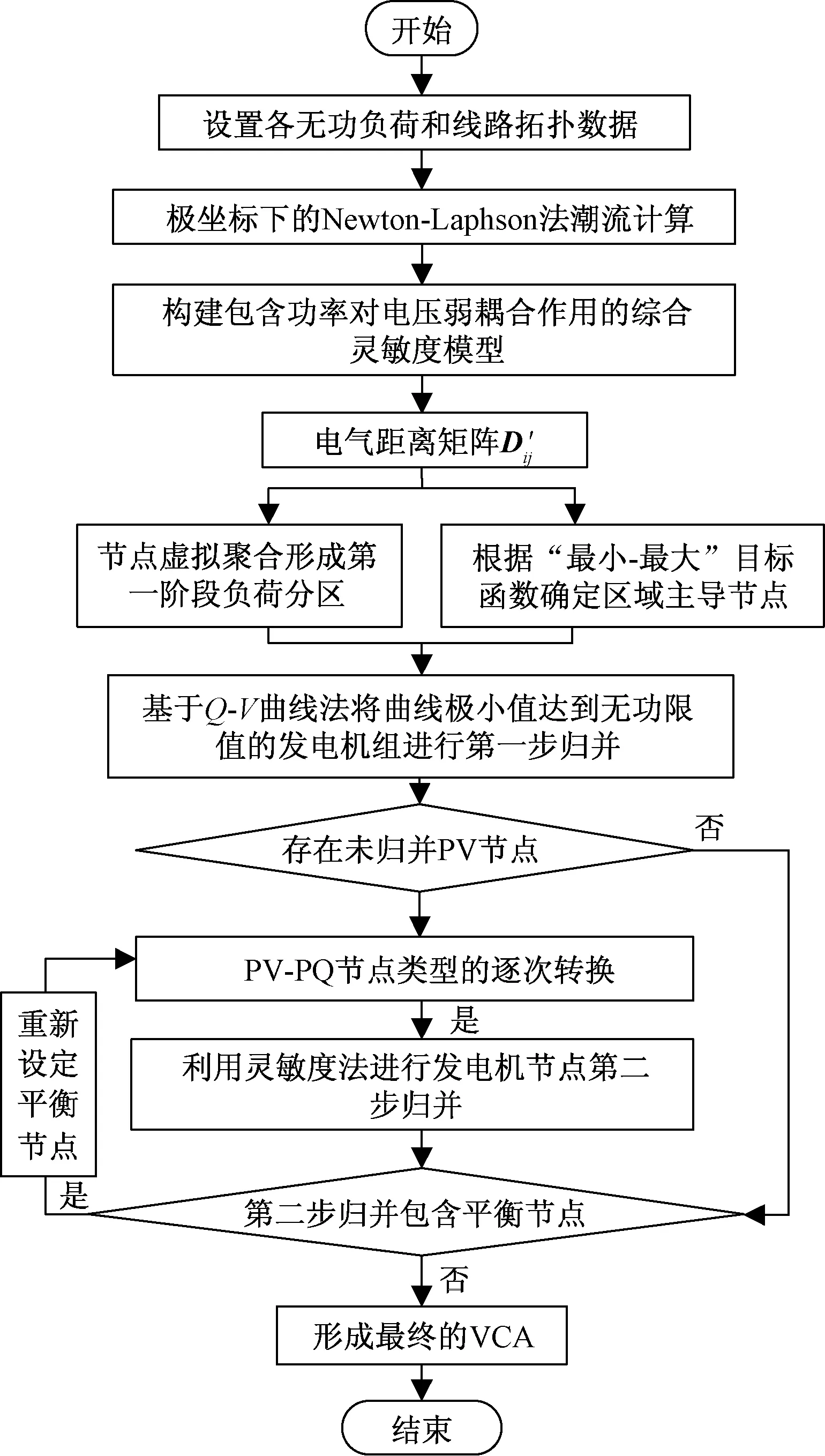
图2 基于综合灵敏度的两阶段电压分区流程图Fig.2 Two-stage voltage partition flow chart based on comprehensive sensitivity

3 算例分析

采用新英格兰39节点系统作为算例，并基于MATLAB进行仿真分析，39节点系统为含有合理发电机节点与负荷节点数量的环网，适用于文中所提出的两阶段分区方法。

3.1 第一阶段分区

新英格兰39节点系统包含29个负荷节点、10个发电机节点(平衡节点31)。首先利用极坐标下的牛顿-拉夫逊法潮流计算得到雅可比矩阵J(67×67)，再利用雅可比子矩阵L、N构建文中所需要的考虑弱耦合关系的综合灵敏度矩阵Svq1(29×29)，其中综合灵敏度矩阵仅包含负荷节点维度的灵敏度元素。

3.1.1 负荷节点分区

以电压衰减量化灵敏度矩阵，通过映射函数与归一化运算得到初始电气距离阵D0。

通过1.3节中节点的虚拟聚合方法对初始电气距离矩阵D0进行迭代，每迭代一次生成一个新的虚拟节点，并需要用最大距离准则重新计算虚拟节点与剩余节点之间的距离。分区个数通常由网络的拓扑结构与分区计算中距离的合并过程决定。

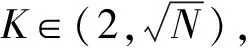
(16)

(2)在进行节点虚拟聚合过程中，记录虚拟节点与剩余节点之间的最大距离，当合并距离的区分度首次明显增大时，指针指向迭代次数对应分区阈值。

由上述两个条件可以得出39节点分区对应的指针j′=24，合适的分区数目为Nz=N-j′+1=6，分区的阈值T=0.52，即当距离矩阵迭代至24时，D24即分区矩阵。

通过1.2节方法得到负荷区域的分区结果，如表1所示。

表1 负荷节点的分区结果

由表1可知，传统分区方法和本文所提方法所得的负荷分区内部节点基本一致，区域边界节点的归属存在差异。结果说明，所采用的综合灵敏度模型能够反映有功功率对电压相差的弱耦合作用，而且满足系统的地理邻近性和区域的连通性，分区结果更合理。

3.1.2 主导节点选择

采用1.3节提出的“最小-最大”准则目标函数可以确定负荷区域的主导节点，从而减少控制节点，以便于电压优化分布控制，并可以为系统的二次规划提供依据。

采用的综合灵敏度模型在不影响无功对电压的主要控制作用情况下，考虑了有功功率对电压幅值的弱耦合作用。因此，所求得的区域内负荷的电压主导节点对区域内的其他节点的灵敏度，反映了其对所在的负荷区域具有电压可控性。由表2～表7可知，主导节点选择结果依次为12、18、20、21、25、28节点。这些节点对于所在区域的负荷节点具有强控制作用，可以作为控制区域电压变化的可控性负荷节点。

3.2 第二阶段发电机归并

通过2.1节中所述的基于电压稳定性下的Q-V曲线法，寻找到满足无功和电压极小值点并且无功限值一致的发电机节点，将其划分为一个区域，得到表8结果。

基于2.2节中无功源控制空间思想，通过发电机-负荷节点类型的转换，构建了包含无功源节点的灵敏度矩阵。由于第二次归并节点并不存在平衡节点，因此不需要重新设定平衡节点。剩余未归并的无功源节点为(30、33、34、37、38与分区结果不一致的39)节点，利用灵敏度法进行逐次归并，实现全网分区的结果如表9所示。

结合第一阶段的负荷分区与第二阶段的发电机节点两步归并，得到最终的全网分区结果如表10所示。

分区拓扑与主导节点的选择如图3所示。

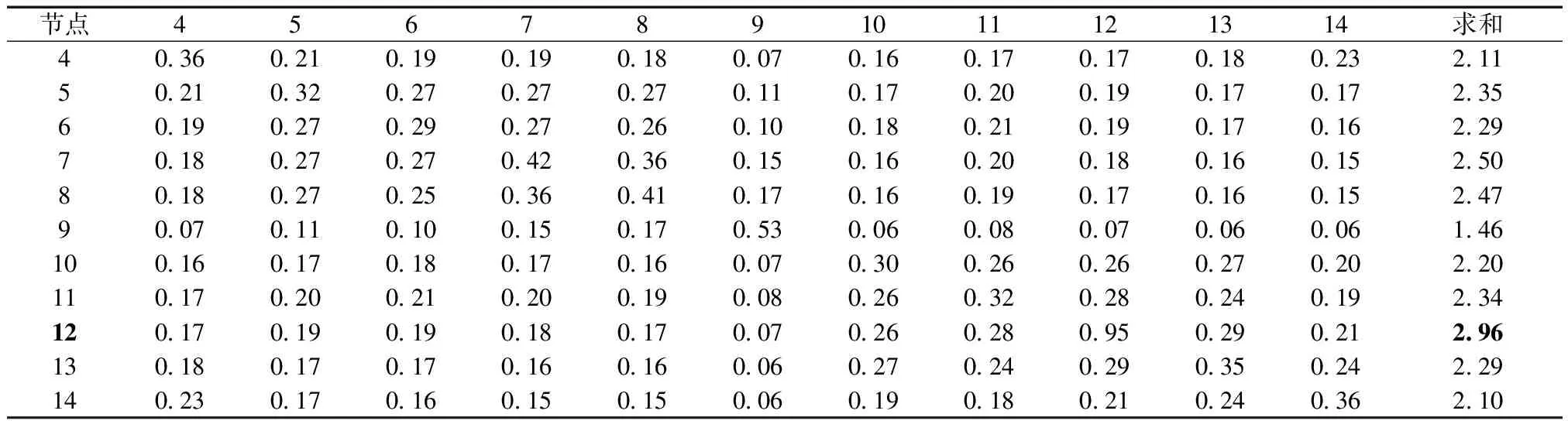
表2 区域1主导节点的选择结果

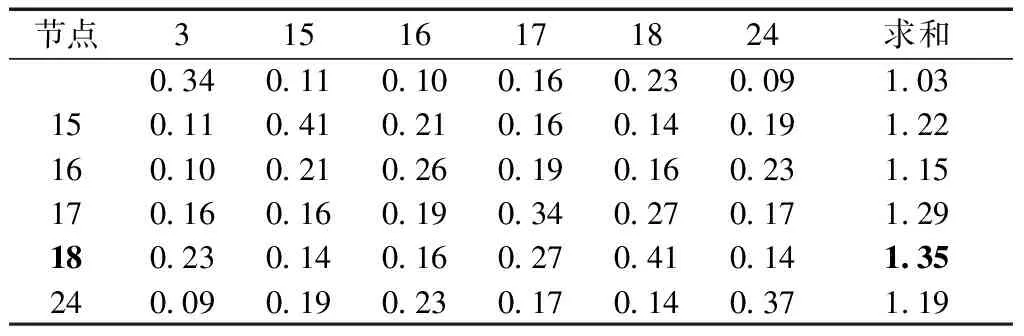
表3 区域2主导节点的选择结果

表4 区域3主导节点的选择结果

表5 区域4主导节点的选择结果

表6 区域5主导节点的选择结果

表7 区域6主导节点的选择结果

表8 Q-V曲线法下的发电机归并

表9 基于无功源控制空间的剩余发电机节点归并

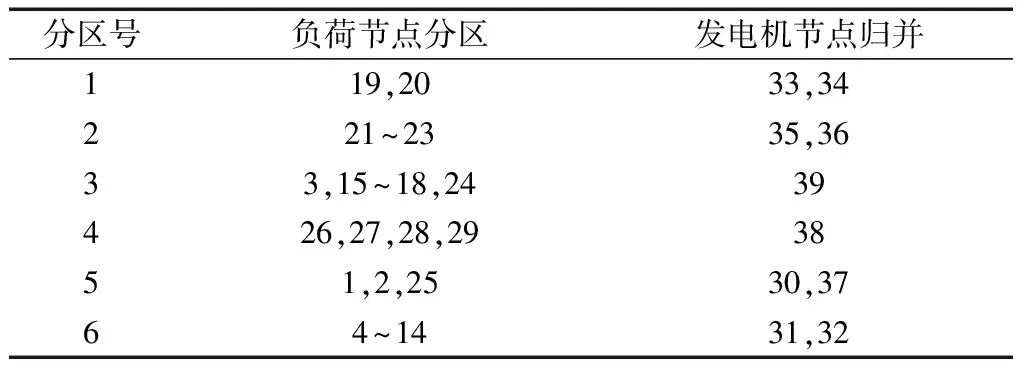
表10 全网分区结果

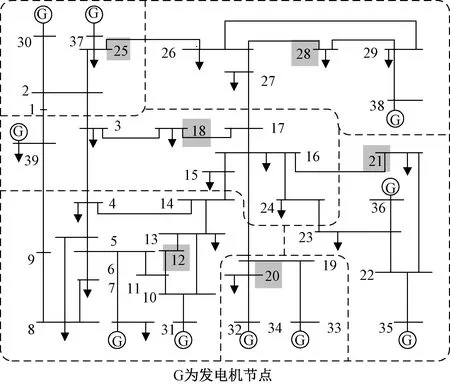
图3 39节点系统分区拓扑图Fig.3 39-node system partition topology diagram

4 结论

提出了一种基于综合灵敏度的两阶段电压控制分区方法，得出如下结论。

(1)所采用的综合灵敏度模型在考虑无功功率对电压主要控制作用下，同时考虑了有功功率因素，能够更全面地反映节点功率与电压的耦合性。

(2)采用综合灵敏度构建“最小-最大”目标函数识别区域的电压主导节点，能简化电压控制的节点数，并为系统的优化配置提供了依据。

(3)第二阶段提出的发电机节点两步归并方法，减小了无功源节点对负荷节点灵敏度的影响，使归并的结果更加合理。