非均匀分布量测下的扩展目标跟踪方法

孙航宇， 马天力， 李继超， 张琪

(西安工业大学电子信息工程学院， 西安 710021)

目标跟踪是通过一系列含有噪声的传感器观测值来估计目标运动状态的技术[1]，其广泛应用于飞行器监视[2]、水下声纳跟踪[3]和无人驾驶等领域。随着相控阵雷达以及X波段雷达[4]等新型高分辨率探测设备的出现，扩展目标(extended target, ET)的概念也随之产生。目标在同一时刻可以产生多个量测值，且量测数量随着目标的姿态变化而变化。相比传统跟踪方法将目标作为质点，这些由同一目标上多个散射源产生的一系列量测信息可以更加准确地描述目标状态。针对该情况，传统点目标跟踪方法由于模型不匹配且计算复杂度过高致使跟踪性能下降甚至失效，难以发挥高分辨率传感器的优势，并且在传感器的扫描周期中，受到噪声影响的空间分布量测值均存在一定偏差[5]。因此，扩展目标的状态估计成为研究的重点和难点。

近年来，相关学者对扩展目标跟踪问题进行了深入研究。Koch[6]将随机矩阵模型(random matrix model, RMM)引入到扩展目标跟踪中，利用随机矩阵来构建目标的外形模型，尽管RMM模型简单且有效，但其并不适用于所有的目标形状。在此基础上，Baum等[7-8]提出了基于曲线拟合方法的随机超曲面模型(random hypersurface model, RHM)，模型通过参数化形状边界来描述目标轮廓，因此RHM模型既可用于对基本凸形状的估计，也可对非凸形的目标建模。此外，Hirscher等[9]提出了高斯过程模型，通过轮廓半径的函数对目标进行建模。随后，一些学者在上述研究基础上进行了更深层的探索，并设计了一系列的复杂外形目标建模方法，如Aftab等[10]改进并提出的混合RHM，Zea等[11]提出的水平集RHM以及Gong等[5]对RMM加以组合后改进的非椭圆RMM等，在保证精度的同时提高了针对不同目标形状的适应性。

对于上述跟踪模型，常采用卡尔曼滤波器以及在其基础上改进的扩展卡尔曼滤波器和无迹卡尔曼滤波器(unscented kalman filter, UKF)[12-14]等高斯估计方法来计算目标状态及形状参数，但是形状模型的复杂度增加会导致传统滤波器的计算性能大幅下降。因此，文献[15]中提到的马尔科夫链蒙特卡罗方法逐步被应用到了形状估计中。Özkan等[16]提出了高斯过程卷积粒子滤波器，该方法在建模过程中不需要任何量测统计量的先验信息和似然函数的表达式，但是存在稳定性较差的问题。Freitas等[17]设计了针对扩展目标的箱粒子滤波器，使用状态空间中非零体积的矩形区域代替传统的量测来处理扩展目标。虽然该方法能对扩展状态进行精确估计，但是随着新生箱粒子数的增加，其计算复杂度会迅速提高。

一般来说，在扩展目标形状的估计过程中，通常需要满足两个假设条件，一是目标表面量测的数量服从泊松分布，二是散射源在笛卡尔坐标系中的位置服从均匀分布。在实际场景中，由于受到雷达方位角的变化和目标表面材料特性分布的影响，目标形状估计所需的量测数据通常无法满足上述假设，导致估计的结果出现较大偏差甚至出现对形状的错误估计。因此，现提出非均匀分布量测下的扩展目标跟踪方法，设计产生均匀分布量测的策略，利用均匀分布的伪量测代替原始量测，通过分层无迹卡尔曼滤波器来分别计算运动状态和形状参数的后验概率，从而降低非均匀分布量测值对目标形状估计的影响，获得准确的目标形状，以期为散射源非均匀分布条件下的扩展目标跟踪提供理论基础。

1 基础理论

假设在k时刻，扩展目标的状态为

Φk=[xk,pk]T

(1)

(2)

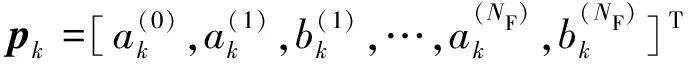
(3)

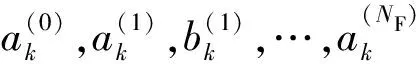
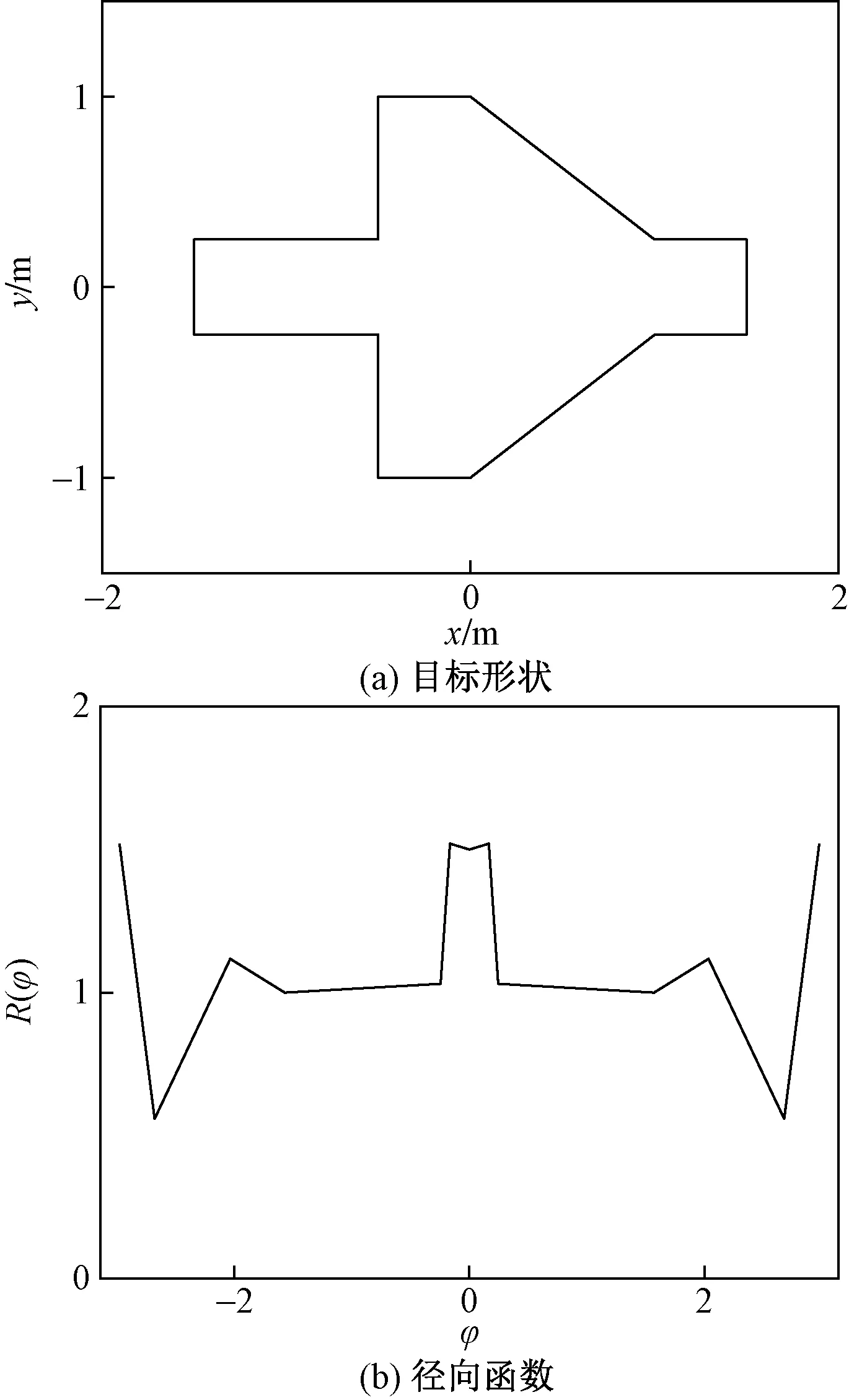
图1 星凸形目标示意图Fig.1 Example for the shape of star-convex extended objects

1.1 量测模型

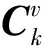
zk,i=yk,i+vk,i

(4)

结合式(2)，散射源的计算公式为

yk,i=R(φk,i)pke(φk,i)sk,i

(5)

(6)

1.2 运动学模型

假设运动参数和形状参数相互独立，并遵循线性马尔可夫模型：

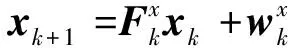
(7)

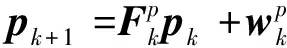
(8)

2 基于星凸RHM的分层无迹卡尔曼滤波器

为了降低非均匀分布散射源对扩展目标跟踪的影响，在前文所述模型的基础上，提出了一种递推估计扩展目标运动状态和形状参数的扩展目标跟踪方法，通过生成均匀分布的伪量测来替代原始量测，并据此推导了分层的无迹卡尔曼滤波器，算法框图如图2所示。

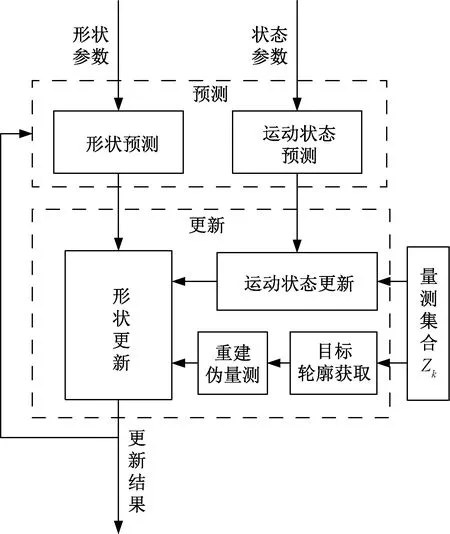
图2 HUKF算法框图Fig.2 Theblock diagram of the HUKF algorithm

2.1 目标轮廓提取

由于伪量测的分布以目标轮廓区域为基准，需要进行轮廓提取，采用质心轮廓距离法来提取目标的轮廓。令分割角度为θ=2π/N，将量测区域划分为N个子区域。在k时刻，根据量测集合Zk计算出每个子区域Ωn中的量测值zk,i到目标质心zc的距离dn,i，从而获得了质心到子区域最大距离的序列[d1,d2,…,dN]。提取的轮廓点集为

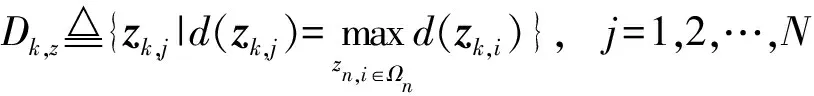
(9)

图3为不同分割角度θ下的轮廓提取结果，如果分割角度越小，对特征的描述会更加细致，获得轮廓越精确。

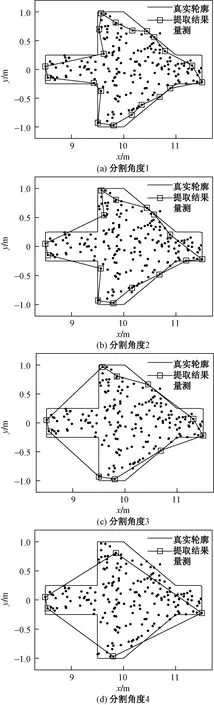
图3 不同分割角度下的轮廓提取结果Fig.3 Contour extraction results for different dividing angle

2.2 伪量测的产生

由于目标表面散射源呈非均匀分布，传统的UKF会造成量测状态估计值偏差过大，导致轮廓估计不准确。因此，通过生成伪量测值的方法来更新形状参数。首先，利用基于坐标排序的Graham-scan算法[19]求出多边形的最小凸包，然后计算出凸面积的最小外接椭圆，最后在边界椭圆内生成均匀分布的伪量测。非均匀分布散射源如图4所示。

假设(X,Y)表示有界区域U中的一个随机点，且X和Y为独立均匀随机变量。根据均匀分布的定义，随机点落入子空间Ui的概率是相同的。基于这一特性，可在最小边界上产生伪量测。利用射线投射方法[20]提取位于多边形内部的量测值，从而产生均匀分布于目标表面的伪量测。伪量测产生流程如图5所示。

图4 非均匀分布散射源Fig.4 Nonuniform scattering source

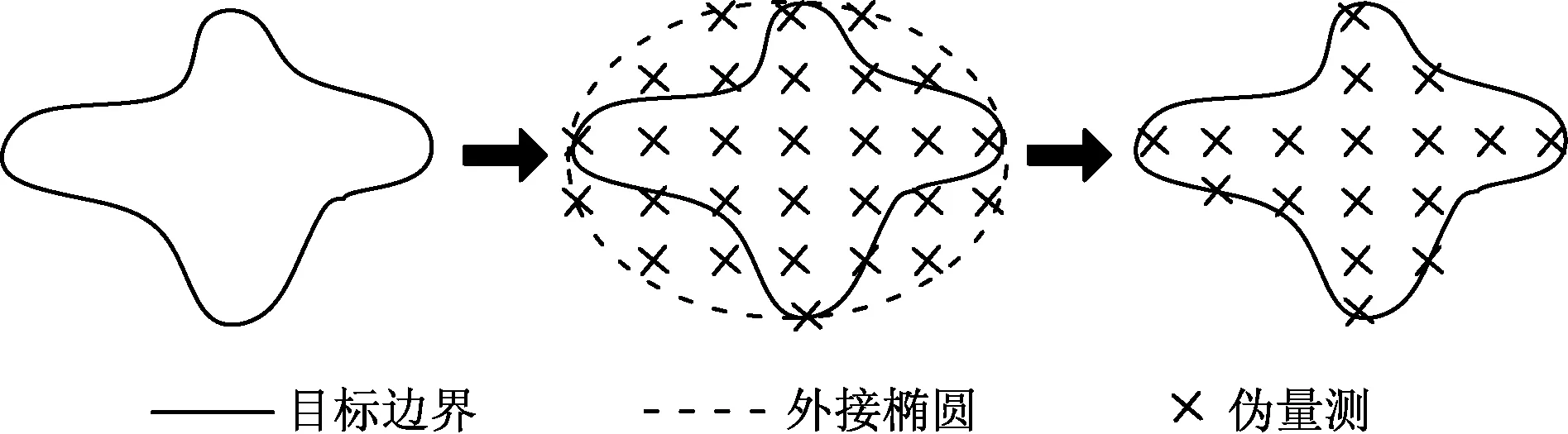
图5 伪量测的产生Fig.5 Pseudo measurement generation

2.3 分层无迹卡尔曼滤波器

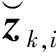
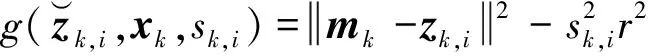
(10)

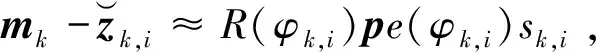
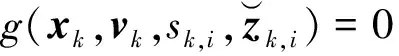
(11)

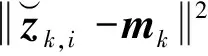
(12)

在更新过程中，上层UKF用于更新运动状态。根据位置更新结果，再利用下层UKF获得形状参数。用于量测预测的采样sigma点计算公式为

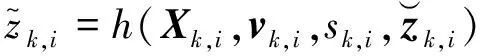
(13)

式(13)中：Xk,i为运动状态的sigma点， 且i=0,1，…,2nx。量测的预测值、协方差矩阵以及互协方差矩阵分别为

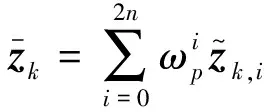
(14)

(15)

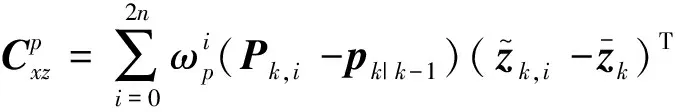
(16)

式中：Pk,i为形状参数的sigma点。形状参数和协方差更新方程为

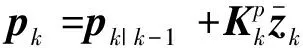
(17)

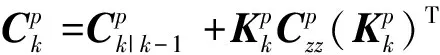
(18)

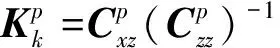
(19)

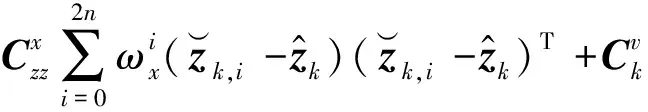
(20)

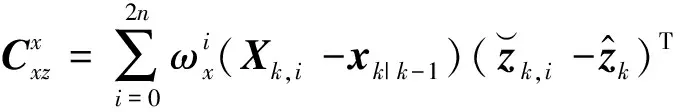
(21)

位置参数和协方差更新为

(22)

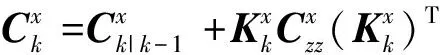
(23)

由于运动状态和形状参数的时间演变均遵循线性模型，故状态预测过程可以表示为

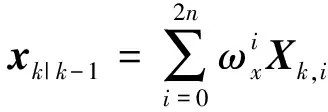
(24)

(25)

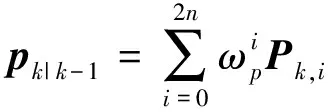
(26)

(27)

3 算法实现与仿真

仿真过程采用混合高斯分布来模拟非均匀散射源分布，设置量测分布角度φ1=N(0.15,0.6)和φ2=N(0.75,0.2)服从混合高斯分布，混合系数为α=[0.5,0.5]。图6和图7分别为原始量测和伪量测的分布对比以及两种滤波器对目标的跟踪结果对比。此外，图8分别给出了所提算法在400次Monte Carlo运行实验下对目标轮廓估计的平均位置均方根误差(root mean squard error, RMSE)以及轮廓MHD。

图6(a)为跟踪过程中第11帧数据中的原始量测分布情况，而图6(b)为经过量测轮廓提取，重新生成的均匀分布伪量测。将两幅图中的量测分布进行对比可以看出，经过所提算法处理过后的伪量测相比原始量测更加均匀、完整地分布于整个目标区域，在后续运动状态和形状参数的估计过程中可以提供更加完整的目标量测信息，降低非均匀量测带来的估计偏差。

图7为HUKF以及传统UKF滤波方法对星凸扩展目标的跟踪结果对比。在图7(a)中，可以看出仿真实验中两种滤波器对目标的整体跟踪效果，根据图中目标估计位置的对比可知，两种滤波器都能够实现对星凸形扩展目标进行较为精确地跟踪。图7(b)为

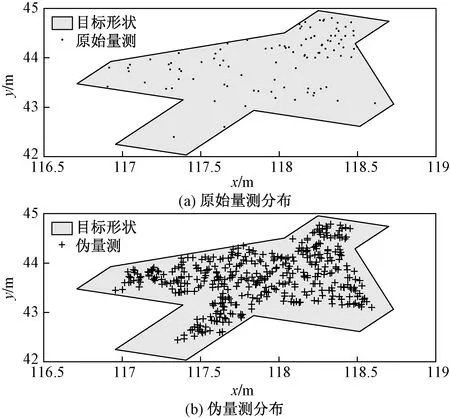
图6 量测分布情况Fig.6 The example of measurements distribution

两种滤波器形状估计结果的局部放大对比图，分别显示了不同滤波器在第7帧和第8帧的收敛情况，可以看出本文所提出的HUKF方法在跟踪过程中能够更加准确地收敛于具有星凸特征的目标形状。

从图8(a)和图8(b)给出的曲线可以看出，跟踪过程中HUKF方法的平均位置RMSE以及MHD都较为稳定，而UKF方法的平均位置RMSE曲线随着目标的转弯运动出现小范围的波动，主要原因是UKF对散射源的统计特性很敏感。通过两种评价指标的对比可知，在量测非均匀分布的情况下，HUKF滤波器的平均位置RMSE以及MHD距离都要明显低于UKF方法。

图7 两种滤波器对目标的跟踪结果Fig.7 Theresults of different filters

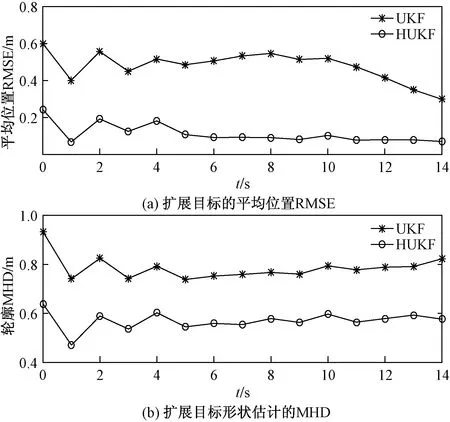
图8 平均位置均方根误差和MHDFig.8 The average position RMSE and MHD

4 结论

针对扩展目标跟踪过程量测分布不均匀导致中目标轮廓估计精度降低的问题，提出了一种非均匀分布量测下的扩展目标跟踪方法。方法通过轮廓质心法和接受-拒绝采样法产生伪量测，解决了原始量测分布不均匀，覆盖边界缺失的问题；通过构建分层无迹卡尔曼滤波器来对运动状态和形状参数分别进行计算，在提高跟踪精度的同时降低了计算复杂度。实验结果表明，HUKF相比于传统的UKF方法，在量测分布非均匀的条件下具有更好的扩展目标跟踪性能。