基于傅里叶变换的光栅衍射分析
王义全,张 颖,陈 笑,邹 斌,蔡园园,王琼千惠,李传波,彭洪尚,黎仪艺
(中央民族大学 理学院,北京 100081)
衍射光栅是基础光学元件之一,在信息处理与分析、生物学、材料学、天文学等诸多领域均有重要应用. 衍射光栅,无论是透射式或反射式,都能通过光栅中的重复结构影响入射光的振幅或相位,导致出射光发生干涉,进而在空间中分离出不同波长的光.按照现代制造工艺的不同,光栅主要有刻划光栅、复制光栅和全息光栅等形式. 随着科技发展及光栅制造技术的不断革新,光栅的应用范围也在不断扩大. 因此,如何使学生理解不同种类光栅衍射的联系与区别,全面系统的掌握光栅衍射规律,对正确使用光栅,尤其是根据需求设计不同形式的光栅结构以及基于光栅衍射的仪器设备均具有重要的意义.
光栅衍射是物理光学教学中的重点与难点之一. 在多数物理光学教程中,光栅衍射的讨论出现2次:1)是在光的衍射部分,利用多缝干涉和单缝衍射的思想,分析了普通透射光栅的衍射场,得到描述光栅衍射场特点的光栅方程;2)是在傅里叶光学中讨论全息余弦光栅的衍射,详细阐述了衍射场与光栅结构之间的关系,得出衍射平面波的出射方向和光栅周期的确定关系.虽然这种分别讨论的方法有利于学生准确掌握不同光栅衍射规律,但使学生容易造成不同光栅衍射所遵循的物理规律不同的错觉. 为使学生全面系统的理解光栅衍射,本文借助于傅里叶分析法,以余弦光栅衍射为基础,分析了常见透射光栅的衍射规律,使学生掌握了两种光栅衍射之间的联系,以期对光栅衍射有更加深入的理解.
1 单一空间频率的余弦光栅衍射特性
余弦光栅是信息技术中常用的一类光栅,多数是透射型.因平面波入射到光栅上,透过光栅的光场复振幅随位置按余弦规律变化而得名. 例如,2束具有一定夹角的平面波入射到照相干板,在干板上发生干涉,产生按余弦规律变化的光强分布,曝光后的照相干板经显影、定影等线性处理后,就可获得一片余弦光栅.该光栅的透过率函数表示为[1]
t(x)=t0+t1cos(2πfx+φ0)
(1)
其中t0为雾底,它表示即使曝光强度为零,冲洗出来的底片在该处仍有一定程度的透过率.t1是透射光强的幅值.它们均是与照相干板的材料及光栅制备过程中曝光时间、显影定影溶液浓度及显影定影时间等因素有关的实数.f为光栅频率.
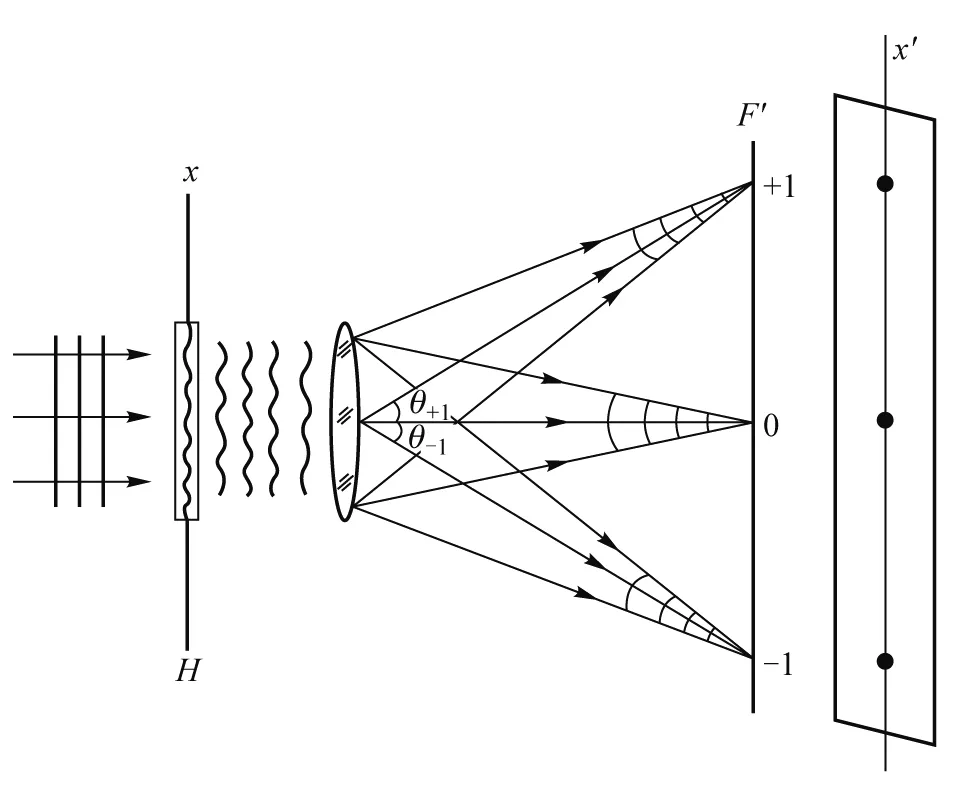
图1 余弦光栅的衍射示意图
设垂直入射于余弦光栅的平面波波前表示为
(2)
经余弦光栅衍射后的出射波的波前为
(3)
式中
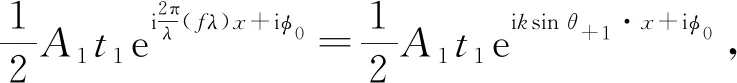
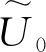
sinθ+1=fλ,
sinθ-1=-fλ
(4)
上式表明,衍射平面波的出射方向角由余弦光栅的频率确定.在光栅周期远大于入射平面波波长的情况下,出射平面波的方向角θ与光栅的空间频率f是一一对应的.
在进行造林之前应该结合地区的实际情况选择优良的树种,坚持适地适树的原则,目的是实现成活率的提升。此外,还应该对当地的环境和土壤的情况进行调查,之后综合考虑选择何种树种。这在一定程度上能够实现病虫害的减少,提高存活率,实现营造林面积的增加。
2 多个空间频率的余弦光栅衍射特性
为进一步证实上述结论,我们以具有多个空间频率的余弦光栅为例进行衍射分析.为不失一般性,我们假设余弦光栅具有3个空间频率f12、f13、f23.当平行光垂直入射该光栅,在衍射场透镜的焦平面上将出现7个衍射斑,即光栅对垂直入射的平面波的衍射场为7个方向平面波的叠加.下面推证各衍射光的出射方向与光栅物理结构之间的关系.
该光栅的透过率函数包括3个空间周期的光栅屏函数,表示为
t(x)=t0+t12cos(2πf12x)+
t13cos(2πf13x)+t23cos(2πf23x)
(5)
当平面波垂直入射到上述余弦光栅,出射场为
t13cos(2πf13x)+t23cos(2πf23x)]=

(6)
由式(6)可见,垂直入射的平面波经余弦光栅衍射后,变成了7列平面波,即一个正出射的平面波和3对互为共轭的平面波叠加. 3对共轭平面波的出射方向与余弦光栅的3个空间频率一一对应,具体表示如下:

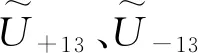

从以上两种余弦光栅衍射场来看,余弦光栅的夫琅禾费衍射场完全是由光栅的物理结构决定,衍射场是若干列平面波的叠加. 如果光栅周期数为k,衍射场中平面波的列数为2k+1,除垂直出射的平面波外,每一列斜出射的平面波的出射方向与光栅的某一周期有确定的对应关系.
3 刻划光栅衍射特性
普通透射刻划光栅是各类基于衍射的光学设备所用的主要衍射元件,也是物理光学中讨论最多的一类光栅.它是由若干个全同的狭缝周期排列而成.设光栅中透光的缝宽为a,两狭缝之间不透光部分的宽度为b,光栅周期d=a+b是光栅的重要参量.我们从多缝干涉和单缝衍射的角度讨论此种透射光栅的衍射场,其光场分布表示为[2]
(7)
(8)

光栅衍射场可以看作光栅强度结构因子和强度单元因子的乘积,衍射光强极大的方位角满足光栅方程:
dsinθk=kλ, (k=0,±1,±2,…)
(9)
从上式可见,在满足光栅方程的方位角上均会出现衍射光极大,即出现一个衍射亮斑.因此,普通透射光栅衍射场中透镜的后焦面上有一系列的衍射亮斑,即普通透射光栅的衍射场是由一系列方向不同的平面波叠加的.平面波的列数、传播方向和光栅周期的个数没有直接从上述公式中反映出来,这似乎和余弦光栅的衍射规律矛盾.为了正确理解周期性透射光栅的衍射现象,对衍射现象有全面统一的理解,我们将从信息分析的角度阐述普通透射光栅的衍射场.
所谓衍射,就是衍射屏对入射波的波前进行调制,在衍射场中形成和入射场差别很大的复杂光场分布. 对于可看作由若干个全同狭缝周期性排列所形成的普通透射光栅,我们假设组成光栅的狭缝边缘对光的传输没有影响,即在整个狭缝上的透过光的振幅相等,由此光栅的结构对入射光波前的调制可近似看作图2所示的矩形波.它的屏函数可写成
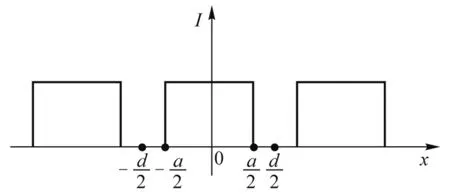
图2 周期为d的矩形波
(10)
在整个光栅范围内,屏函数可以看作一个周期函数. 我们把该函数进行傅里叶展开:
(11)
其中ω=2πf,f=1/d为光栅的空间频率,各级傅里叶展开系数表示为
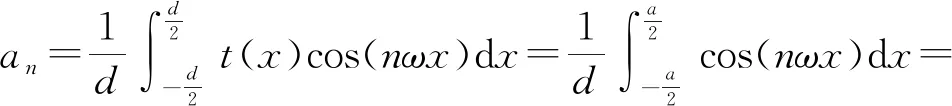

由此,在刻划光栅衍射中,光栅的屏函数可以写为
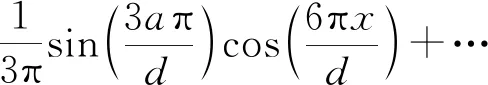
(12)
由式(12)可见,刻划光栅可以看作一系列空间频率倍增的余弦光栅的叠加.
(13)
从式(13)可见,垂直入射的平面波经透射光栅衍射后,变成了(2k+1)列平面波,为包含一个正出射的平面波和2k列斜出射的平面波的叠加.出射平面波的方向满足
sinθk=kfλ, (k=0,±1,±2,…)
(14)
将f=1/d代入上式,得到dsinθk=kλ,这就是光栅方程.
从上述分析可以看出,刻划光栅的衍射场也是一系列平面波的叠加,每一列平面波的传播方向满足光栅方程.另一方面,它同样反映了光栅对入射平面波波前的调制.这个调制把光栅的结构信息加载到输入信号内,在输出信号中反映出来.虽然透射光栅在形式上只有一个空间周期,但这种结构对波前的调制作用,可以看作很多基元周期函数对入射信息作用结果的叠加,所以在衍射场中把各个基元周期函数对入射波的调制作用反映出来,虽然只有一个空间周期,在衍射场中却有多个基元周期函数周期性的平面波产生,在透镜的后焦面上出现多个衍射斑.
4 结论
借助于傅里叶分析法,我们探讨了普通透射刻划光栅衍射场,把余弦函数看作基元函数,透射光栅对入射波前的调制作用作为众多基元周期函数对入射波前调制结果的叠加,从而在衍射场中反映出衍射光栅中所包含的对入射波起作用的所有结构信息.利用这一结果,我们很容易将教学中讨论的两类光栅衍射统一起来,同时也为分析其他形式的光栅衍射,特别是为实现特定衍射场设计的特种光栅提供了指导作用.

