有限平面波叠加模拟中低频混响声场的方法

朱卫红，高 强，邹元杰

（1. 北京空间飞行器总体设计部，北京 100094； 2. 中国航天科工防御技术研究院，北京 100039）

0 引言

在航天任务过程中，航天器能否经受住发射段严苛的力学环境考验，是决定任务成败的关键因素之一[1]。而噪声环境是其中最为典型的一种动力学环境，可能造成机电设备、光学仪器、电子电路等的失效或性能下降，以及部分部组件（如天线、馈源等轻质薄璧结构）的结构性破坏。

噪声载荷的分布频段较宽（20 Hz～10 kHz）。航天工程中针对不同的频段采用不同的分析方法进行声振力学环境预示[2-3]：在低频段采用结构有限元-声学边界元方法建模，即航天器结构采用有限元方法、航天器的内外声场采用边界元方法[4]；在中频段采用有限元-统计能量分析方法建模，即对模态密度较低的结构、关键设备等采用有限元方法，对高模态密度结构和声场采用统计能量分析法[5]；在高频段主要采用统计能量分析方法建模[6]。不论采用哪种方法，都需要建立准确的噪声载荷模型。

目前，通常采用扩散声场（DAF）载荷方法建立噪声载荷模型，假定噪声空间为完全混响空间，基于直接场与扩散声场的互易关系，将声压转化为网格节点上的力谱，直接施加在结构上求解[7]。该方法能够描述声场载荷的空间相关性，但是只在其施加的区域内满足，无法刻画混响声空间中由于结构存在导致的声场不均匀性；另外该模型主要面向结构的承载，无法考虑结构本身的声辐射、散射特征，因此需要结合半无限声场系统来模拟结构的声辐射等特征[8]。而采用平面波叠加模拟噪声载荷，能够刻画整个声空间的载荷空间相关性。这种噪声载荷模型结合有限元-边界元模型，可充分刻画声散射、辐射和声载荷的不均匀性，但与DAF 不同的是只能施加在声学边界元模型中。高强等[9]研究了平面波叠加对声场载荷的空间相关性影响，证明该方法能够准确描述载荷的空间特征，但是如何基于该方法建立混响载荷模型尚未得到解决。

本文提出采用基于随机相位的平面波叠加方法建立中低频混响载荷，结合传统结构有限元-声学边界元模型建模方法进行声振响应预示。文中对基于平面波叠加的混响载荷建模方法的理论、空间特征及平面波数目的确定方法进行详细的研究，并结合实际工程算例验证该方法的可行性与有效性，可为后续的航天工程应用提供支撑。

1 基于平面波叠加的混响载荷建模

1.1 多列平面波叠加的声能密度

混响声场是一种理想的声场，在声场各个位置处，声能量向各个方向的传播概率相同，平均声能密度处处相同。设在声场中有一足够小的体积元，声压为p，空气密度为ρ0，则其声能密度为

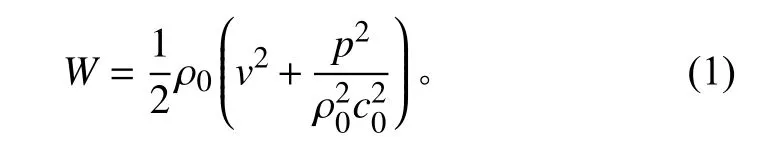
式中：v为体积元速度；c0为空气中的声速。

定义平面波的声压[10]为

式中：x、y、z为空间位置坐标；t为传播时间；P0为平面波声压幅值；ω为平面波的角频率；φ0为初始相位；k为波数；α、β、γ为平面波传播的方向角。

对固定空间位置的平面波，在1 个振动周期T内求取其声能密度的平均值，有

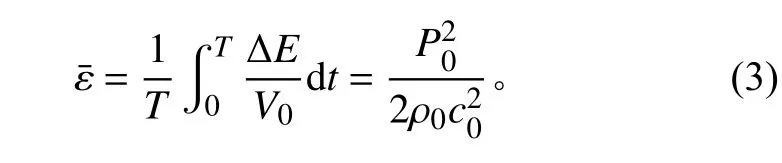
式中：T=2π/ω；ΔE为平面波的能量；V0为声场的体积。可以看出，平面波的平均声能密度仅与其声压幅值有关，而与相位和位置无关。

对于具有相同波长的2 列平面波，在该位置处的声压为

在1 个周期内对声能密度进行平均，有

式中：

如果相位 φ1和 φ2平均分布在区间[0, 2π]内，则相位相干函数的均值为0，即

则

因此，对于具有随机相位的2 个平面波之总成，其1 个周期内的平均声能密度等于其中每列平面波平均声能密度的线性叠加。同理可以推得，对于n个平面波之总成，其1 个周期内的平均声能密度为

1.2 基于混响载荷声压的平面波分布设计

1.1 节的分析表明，在各个平面波相位随机的情况下，平面波的声能密度满足线性叠加原理。

假设将整个声空间建立在球坐标系中，将声空间球面按照经度和纬度进行切分，将纬度分为m层，则每层之间的角间隔为Δθ=π/m，θi=Δθ/2+(i-1)Δθ, (i=1, ···,m)；将经度分为n层，每层之间的角间隔为Δψ=2π/n，ψj=Δψ/2+(j-1)Δψ, (j=1, ···,n)。如图1 所示，假定球坐标的中心为物理坐标原点，令纬度为θi、经度为ψj位置的声压幅值为Pij，其空间矢量方向为

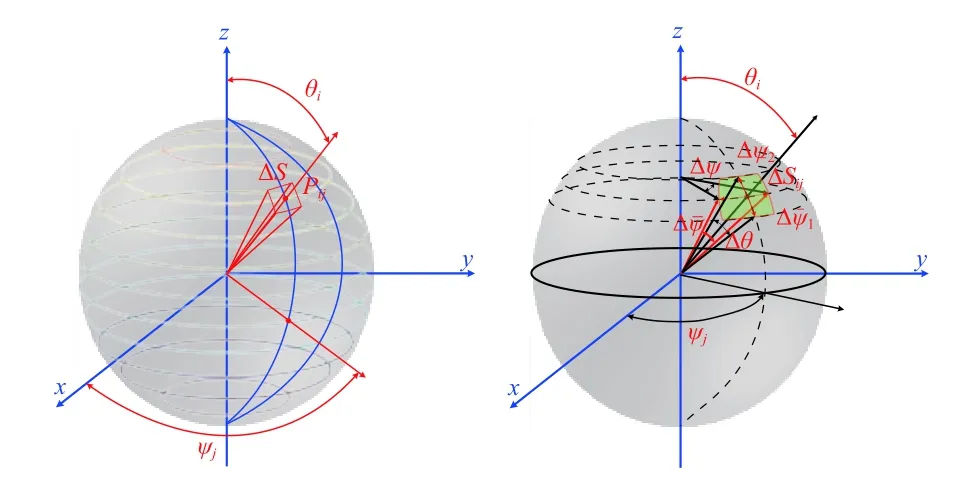
图 1 平面波位置及其有效辐射面积示意Fig. 1 Locations and effective action area of plane waves

平面波将球体分为m×n份，假设平面波Pij作用在球面上的面积为Sij，面积元在纬度方向上的球面宽度为Δθ。因此，平面波Pij在球面上的作用面积近似为

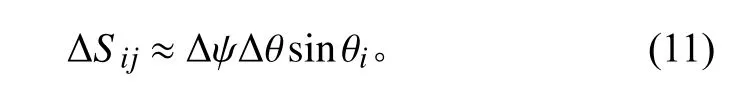
为了保证混响场在球面上的能量均匀分布，须满足：

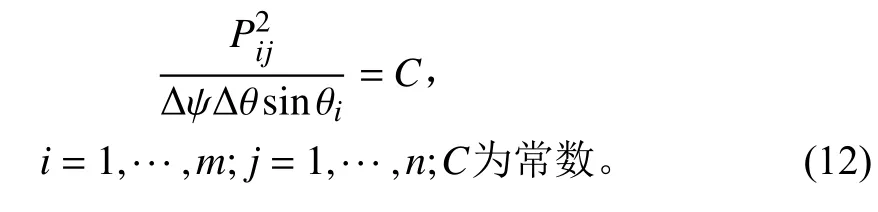
对于具有均匀分布随机相位的平面波，其平均声能满足线性叠加关系，即

因此，每个平面波的声压幅值可以表示为

例如，取n=m=2，计算得到θi=[45°, 135°]，ψj=[90°, 270°]，P2=1，则不难计算得到：

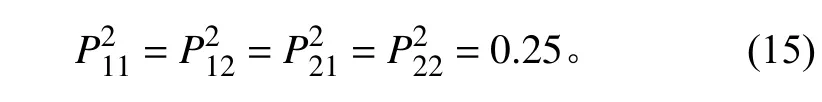
图2 为平面波在整个球面上的声压贡献量分布，可以看出，采用经纬度划分的方式，球面的两极位置声压幅值非常小，赤道附近声压幅值最大。这是由于在不同的位置，平面波之间的间距和有效面积不同导致的；如果采用球面等分方式确定平面波位置，那么球面上的声压将会平均分布。

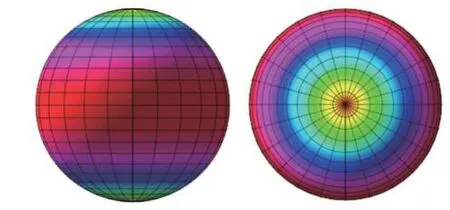
图 2 平面波在球面上的声压幅值分布Fig. 2 Acoustic pressure distribution on the spherical surface

2 基于平面波叠加的混响场空间特征分析

根据式(10)，可计算得到波数在3 个轴方向上的分量，对于平面波Pij，有：

假设在结构表面有l个节点，则每个节点处的声压值为

声压的互谱功率谱密度为

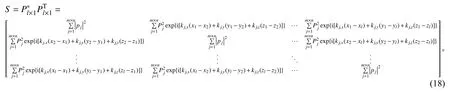
其中非对角元素代表的是空间任意两点之间的互谱密度。设节点u和v之间的矢量为r，定义其与平面波方向的夹角为βj，则互谱功率谱密度可简写为

将式(14)代入式(19)，则有：

设矢量r的方向角为[ε,ς]，则有：

当m→∞,n→∞时，Δθ→0, Δψ→0，则求和可近似用积分表示，

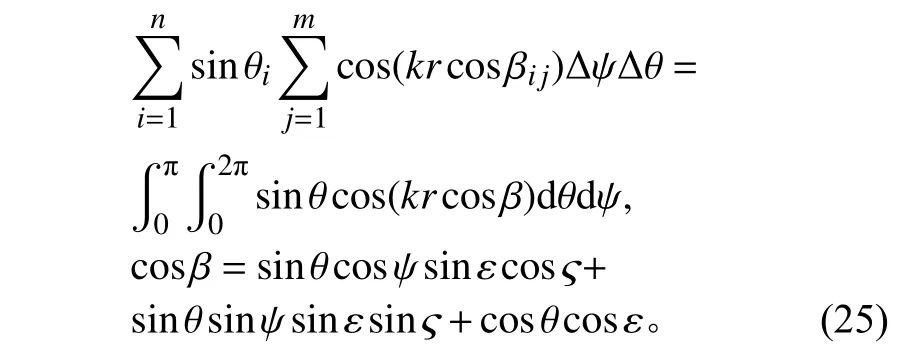
因此，可将式(20)改写为

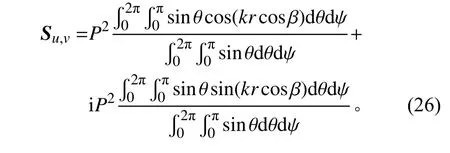
3 平面波叠加的混响声场空间特征验证与数目确定方法

3.1 平面波叠混响载荷的空间相关性分析

公式(26)无法直接进行积分计算，需要作一些数学处理。在此考虑取系统坐标系的z轴与距离矢量r重合，矢量r与矢量k之间的夹角为θ，因此有cosβ=cosθ，则式(26)中的各项积分可写为：

则有

根据空间相关性系数的定义

上述结论与理论解[11]完全一致。

对于任意空间矢量r，无法直接获得解析解，这里采用数值解法验证对于任意的空间两点均满足理论相干系数。图3 为空间矢量r=[172.35°,347.35°]无限多平面波叠加模拟的空间相关性与理论相关性的对比结果，可以看出，不论是随着波数k的变化还是随着距离r的变化，无限多平面波叠加模拟的空间相关性与理论相关性的误差均小于10-4dB。

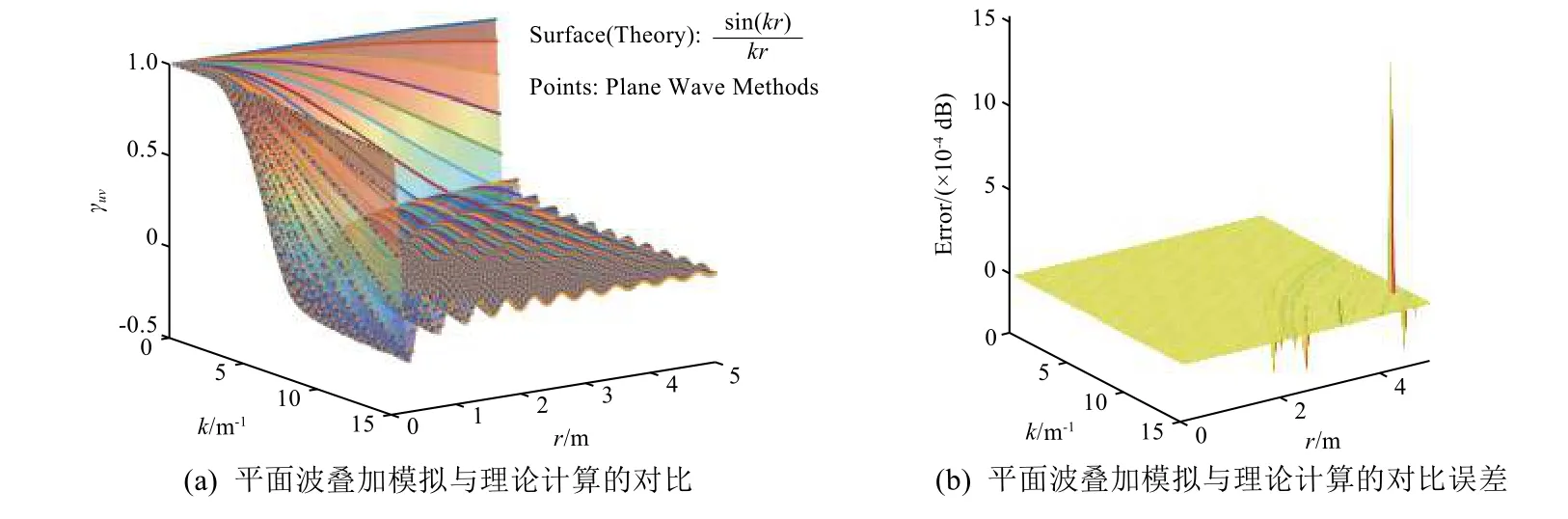
图 3 任意空间矢量r 的空间相关性（无限多平面波叠加模拟与理论值的对比）Fig. 3 Spatial correlation coefficient of an arbitrary vector

理论上，当整个空间中分布无限平面波时，其叠加结果满足理论空间相关性，而幅值是通过对已知混响声压进行分解得到，因此其叠加声压与实际混响声压也是相等的。然而在实际的工程应用过程中，混响场只能采用有限的平面波叠加进行近似，因此其空间相关性会存在一定的建模误差，下面对误差进行分析。

图4 为针对固定的空间矢量r，当平面波数目n分别为2、8、16、32 时，通过Monte Carlo 仿真（仿真次数250）得到的平面波叠加的声场空间相关性随着(kr)的变化。可以看出，平面波数目越多，模型与理论解越吻合，n=32 时基本与理论解一致。因此，采用有限数目的平面波叠加模拟混响场时，模型的空间相关性与平面波数目n、空间点位置矢量r相关；但是随着平面波数目的增加，两者的影响越来越小。

图 4 空间相关性与平面波数目和位置矢量的关系Fig. 4 The spatial correlation coefficient against the number and the location vectors of plane waves

3.2 平面波数目的确定方法

一般而言，采用声学边界元和有限元建模用于低中频的声振耦合分析，而平面波的数目与分析频率的上限和航天器结构的特征尺寸（最大包络尺寸）密切相关。以分析频率上限和结构最大包络尺寸为参数，以空间理论相关性为目标函数，以经度与纬度的平面波数目（二者相等）为自变量，确定使得目标函数满足给定误差。容差函数是具有多个零点的振荡函数，在零点处无法定义相对误差；考虑到空间相关性最大值为1，并随着分析频率与空间距离的增加逼近于0，因此取绝对误差。这里仅给出绝对误差为0.01 的结果：

图5 为容差为0.01 时，平面波数目n与最大包络尺寸r和分析频率上限f的关系。为了便于工程应用，采用二次曲面进行拟合，n、r、f满足如下关系：

其中：

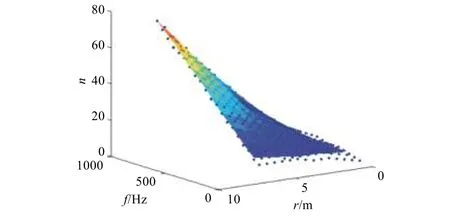
图 5 平面波数目n 与最大包络尺寸r 和分析频率上限f 的关系（容差0.01 时）Fig. 5 The number of plane waves vs. the max envelope size and the top analyzing frequency

根据公式(31)确定的平面波数目叠加后，模型的空间相关性基本与理论解吻合，参见图6。

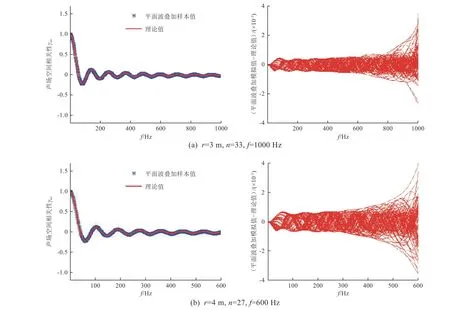
图 6 根据拟合公式确定的平面波数目叠加后模型的空间相关性Fig. 6 The spatial correlation of the model by superimposed plane waves determined by the fitting equation

本文提出的方法偏于保守，而且给出的经验公式假定经度方向和纬度方向的平面波数目相同。在实际工程应用中，需要通过多次不同的平面波数目仿真进行对比分析，最终综合精度和运算的要求，确定合理的平面波数目。

4 工程应用与验证

下文将依据本文提出的混响载荷建模方法，结合混合有限元-边界元建模方法，开展混响载荷的声学特征与航天工程应用案例分析，验证方法的有效性。

4.1 多列平面波叠加模拟混响声场

图 7 平面波叠加模拟混响声场的声压分布Fig. 7 Pressure distribution of reveberant sound field overlayed by plane waves

针对声场中的方形障碍物，采用多列平面波叠加模拟混响载荷分析障碍物对声场的散射效应。图7 为多列平面波叠加后不同频率下整个声空间的声压分布。由图可以看出：整个声空间的声压与期望声压（1 Pa2/Hz）基本一致，声压分布均匀；在障碍物或者结构表面仍有明显的硬边界效应，不同的频率下硬边界效应的区域分布大不相同，因此如果直接在结构表面施加等效的声压载荷，可能无法准确描述该特征。

4.2 低频混响载荷的遮挡效应模拟

采用平面波叠加模拟混响场可刻画复杂结构在混响声场中由于其几何构型导致的遮挡效应，如果直接在结构表面施加声载荷则无法刻画之。以某结构尺寸为0.5 m×0.5 m×4 m 的复杂构型结构（参见图8）为例，研究在混响载荷（多列平面波叠加模拟）下的声场声压分布情况。图9 所示为在不同频率下结构遮挡效应引起的声压分布：由于构型原因，在不同位置不同频率下声压的分布差异较大，尤其是在低频下，窄小声腔结构引起的声压放大达到15 dB。这可能是低频结构由于声载荷导致破坏的原因之一。

图 8 遮挡效应分析模型Fig. 8 Illustration of masking effect

图 9 不同频率下结构遮挡效应引起的的声压分布Fig. 9 Pressure distribution change of different frequencies due to masking effect

4.3 太阳电池阵声振响应分析与验证

采用某平台的太阳电池阵模型进行噪声试验，每块电池阵由内外2 块板构成。试验时，南北太阳电池阵同时安装在模拟墙上，如图10 所示。根据试验要求在太阳电池阵外侧板布置约10 个测点，太阳电池阵的声振响应以面外响应为主，因此主要考察面外响应，测点布置如图11 所示。仿真载荷采用试验给定条件确定：试验条件为远场声压，因此边界元载荷定义时采用远场声压；试验条件是在倍频程下给定的，因此需要通过计算转换为4 Hz 等带宽的载荷；为了模拟测量噪声，在载荷中引入噪声。

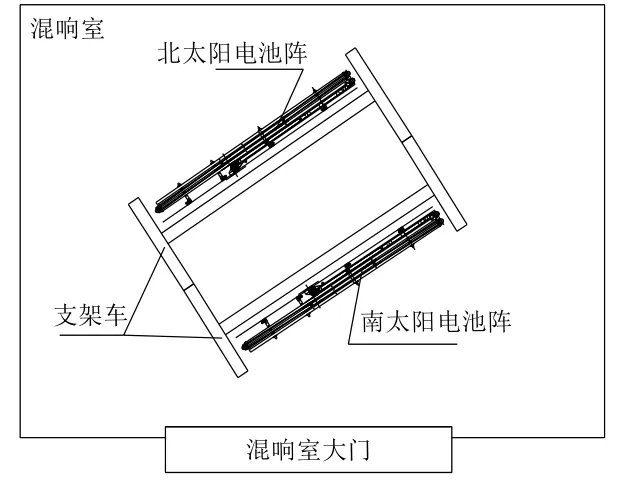
图 10 太阳电池阵试验状态Fig. 10 Acoustic test of solar panels

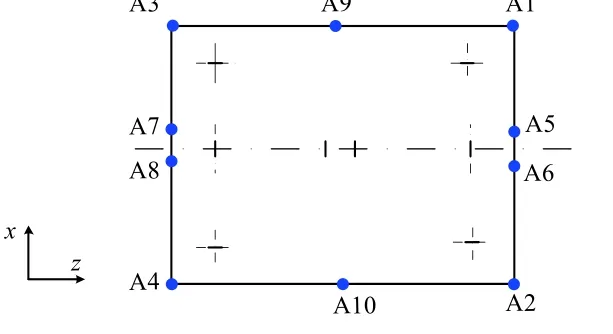
图 11 太阳电池阵测点布置Fig. 11 Locations of sensors on the solar panel

通过对仿真分析结果对比观测发现，测点的位置摄动对预示结果的影响较大，因此在测点附近选取多个测点测量结果与试验结果进行对比。太阳电池阵上10 个测点的加速度响应结果如图12 所示。可以看出：基于本文提出的混响载荷建模方法能够准确描述太阳电池阵声振试验所经受的声载荷，预示结果与试验结果基本吻合。为进一步分析测点位置精度对仿真结果的影响，图13 给出了测点8 附近15 个不同位置的响应预示结果与试验值的总方均根误差，发现最大误差大约为4 dB，南板与北板的误差分布基本一致，仿真模型与实际结构的测点位置存在的偏差会对仿真结果的准确性造成一定的影响。总体而言，在实际工程应用中可以通过改善模型精度、声载荷谱的准确程度以及测点的位置精度来不同程度地提高预示结果的准确度。

图 12 太阳电池阵加速度响应Fig. 12 Acceleration responses of the solar panels

图 13 测点8 附近不同位置的声场响应预示误差Fig. 13 Influence of sensor location on the RMS vibroacoustic response of the sound field

5 结束语

本文提出在平面波中引入随机相位，通过平面波叠加模拟航天器经受的混响声场载荷；当平面波的数目足够多时，则整个声空间的分布特征满足理论空间相关性，能够较为准确地模拟低频段的声空间模型。

数值算例分析表明：1）采用随机相位的平面波叠加的混响载荷建模方法，整个声空间的声压与期望声压基本一致。与传统分析中将硬边界效应定义为刚性边界放大3 dB 不同，基于本文方法能够明显观察到结构周围的硬边界特征，得到的硬边界效应是随着频率变化的，其规律有待于进一步深入研究。2）本文提出的建模方法能够描述复杂结构几何形状引起的遮挡效应，因此能够改善中低频声振预示的精度。

实际工程应用案例表明：试验结果与采用本文方法建立混响载荷模型进行声振预示的分析结果基本吻合，验证了本文方法的有效性。但传感器的位置误差会对分析结果有一定的影响，应予以关注。