基于超声导波的返回舱热防护结构烧蚀层厚度监测方法

张佳奇，刘明辉，刘科海*，冯咬齐，杨正岩，郑跃滨，武湛君

（1. 大连理工大学 工业装备结构分析国家重点实验室，大连 116024；2. 北京卫星环境工程研究所，北京 100094）

0 引言

航天员乘坐的返回舱在返回地球时以高超声速穿越大气层，气动加热下其表面温度极高。为阻止气动加热产生的热量传入舱内部，返回舱表面设计有热防护结构，以保证航天员的生命安全和舱内仪器设备正常运行[1-2]。

热防护结构采用的防热材料主要有适用于相对温和再入环境的可重复使用的非烧蚀防热材料以及适用于高加热速率热载荷的轻质烧蚀热防护材料。前者曾是航天飞机高温区和大面积区域所用的重要热防护结构材料[3]；后者一般以酚醛树脂、环氧树脂或硅橡胶等作为基体，以纤维、酚醛微球、玻璃微球等作为增强材料或填充剂复合而成，尽管不能重复使用，但具有安全、可靠、适应性强等特点[4]。树脂基材料在烧蚀环境下能发生多种吸收热能的物理和化学变化，借材料自身的质量消耗带走大量热能，以达到阻止热流传入结构内部的目的[5]。考虑载人飞船返回舱再入的特点以及高可靠性的要求，目前采用树脂基复合材料作为主要防热材料是一种较可靠的优选方案。

在热防护结构设计和测试阶段已经做了大量的结构优化、载荷试验等工作，然而航天器升空后的服役情况非常复杂，热防护烧蚀层可能面临恶劣的实际工况；一旦发生异常，就可能导致热防护结构在再入的过程中整体失效，引发事故甚至造成人员伤亡[6]。美国“哥伦比亚号”航天飞机即在返回大气层时因表面绝热材料脱落而解体坠毁[7-8]。因此迫切需要发展有效技术手段对返回舱主要热防护结构进行实时监测与性能评估，以便及时发现和控制风险。

烧蚀材料层厚度是返回舱热防护结构主要监测的对象之一[9-10]。目前已有多种可用于航天器结构的健康监测技术，如光纤技术[11]、涡流技术[12]、机械阻抗技术[13]、声发射技术[14]及超声导波技术[15]等，其中超声导波可实现长距离低衰减传播，并具有监测范围大、结果准确、易于结构集成等优点，被认为是最具应用前景的结构健康监测方法之一[16-18]。目前基于超声导波的返回舱结构健康监测的研究报道还不多见，其主要原因在于返回舱结构通常为结构本体层（金属）与防热层（非金属）组成的复合结构，其超声导波传播特性较单层材料板更复杂，需要深入研究复合结构中超声导波的传播特性，以发展烧蚀层厚度变化在线监测技术，为返回舱结构提供安全性保障，并为热防护结构设计的可靠性评估提供重要数据反馈。

本文首先阐述双层结构中超声导波频散曲线的理论计算方法，进而根据双层结构中超声导波的传播特性分析热烧蚀材料厚度表征方法，提出基于波速变化的热烧蚀材料厚度监测策略，最后进行有限元模拟验证和实验验证。

1 双层热防护结构中的导波传播特性

1.1 结构模型

热防护结构防热层（非金属）与返回舱结构本体层（金属）通过柔性胶黏剂连接组成双层复合结构。本文通过半解析有限元（SAFE）法对双层复合超声导波频散曲线开展研究。

定义波导截面为yz平面，沿y方向板宽无穷大，波传播方向为x方向，如图1 所示。

波导中各质点谐波位移分量、应力分量和应变分量分别为：

σ= ˜Cε ˜C

由本构关系 ， 为材料应力-应变关系矩阵，可知应变ε可由简谐位移u表示为

波导介质中任意一点的应变能为

其中V为体积。

波导介质中任意一点的动能为其中ρ为质量密度。

将式(6)和式(7)代入哈密顿方程[11]

中，得到

假定沿x方向传播的位移场是简谐的，用空间函数表示yz截面的幅值

其中：ξ为波数；ω为频率。

波导结构截面Ω可以用通过有限元方法离散后的Ωe来表示，即采用一维三节点单元对薄板的横截面作有限元离散[19]，每个节点有3 个自由度，分别对应3 个方向的位移。对波导介质的横截面作有限元离散后，单元e内任一点的位移可以通过形函数表示为

建立特征方程

式中：

其中：ne1是单元总数；

最后得到一般特征方程

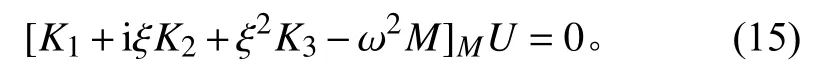
1.2 双层结构频散曲线计算

为了简化特征方程求解，需要消去式(15)中的虚数项，故引入辅助矩阵T，其具有如下性质：TT=T*，T*T=TT*=I。利用辅助矩阵进行如下变换：

将式(16)代入式(15)得：

相速度定义为

群速度定义为

为简化求解步骤，需对所求结构的频散曲线中的所有导波模态进行分离，可采用Bartoli 等[19]的方法计算

基于半解析有限元法可以求解导波在双层复合结构中传播的频散曲线，材料参数见表1。铝/PICA（酚醛树脂基材料）双层结构以及铝/E51（环氧树脂基材料）双层结构的导波频散曲线分别如图2 和图3 所示。由于双层材料弹性模量、密度等力学性能参数差异较大，与单层铝结构的导波频散曲线有一定的差异。因此，可由导波频散曲线分析不同材料、不同结构内导波的传播特性，并根据传播特性来设计针对特定结构多种损伤类型的监测方法。

表 1 双层复合结构材料参数Table 1 The physical parameters of double-layer composite structure

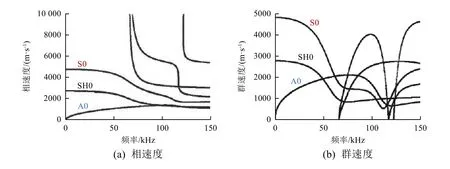
图 2 铝/PICA 双层结构的导波频散曲线Fig. 2 Guided wave dispersion curves of Al/PICA double layer structure

图 3 铝/E51 双层结构的导波频散曲线Fig. 3 Guided wave dispersion curves of Al/E51 double layer structure

2 烧蚀层厚度监测方法

2.1 监测原理

超声导波在板中传播特性与板厚相关，传播速度随着板厚的变化而变化。本文以铝/E51 热防护双层板为研究对象，且假定在厚度缺失过程中结构材料属性不变。图4 为不同烧蚀材料厚度的双层板的导波频散曲线，图中箭头方向表示同一频率下烧蚀层厚度不断减小。可以看出导波的传播速度随着烧蚀层厚度的减小而增大。

图 4 不同烧蚀材料厚度双层板的导波频散曲线Fig. 4 Dispersion curve of double layer plates with different thicknesses of ablation materials

根据导波传播速度随基体/烧蚀材料双层复合结构中烧蚀材料层厚度减小而增大的特点，设计出如图5 所示的基于超声导波的热防护双层结构烧蚀层厚度监测流程。

图 5 基于超声导波的烧蚀层厚度监测流程Fig. 5 The flow diagram of guided wave based ablation layer thickness monitoring

2.2 监测模态和频率选择

超声导波频散曲线和厚度敏感度可作为厚度监测的模态和频率选择依据。根据半解析有限元计算得到的频散曲线数据可以得到导波的厚度敏感度曲线，如图6 所示。可以看到：S0 模态是最快的模态，其厚度敏感度明显优于A0 模态；并且S0 模态主要振动模式为在面内沿着传播方向振动，可以被压电传感器采集，因此选取S0 模态对热防护结构烧蚀材料厚度进行监测。由图6还可看到，随着频率的增大，S0 模态厚度敏感度有所增大，敏感度曲线的线性度变差，模态数量也会变多。本研究针对烧蚀层厚度在5 mm 内的变化进行监测，故综合考虑选取40 kHz 频率进行烧蚀层厚度监测。

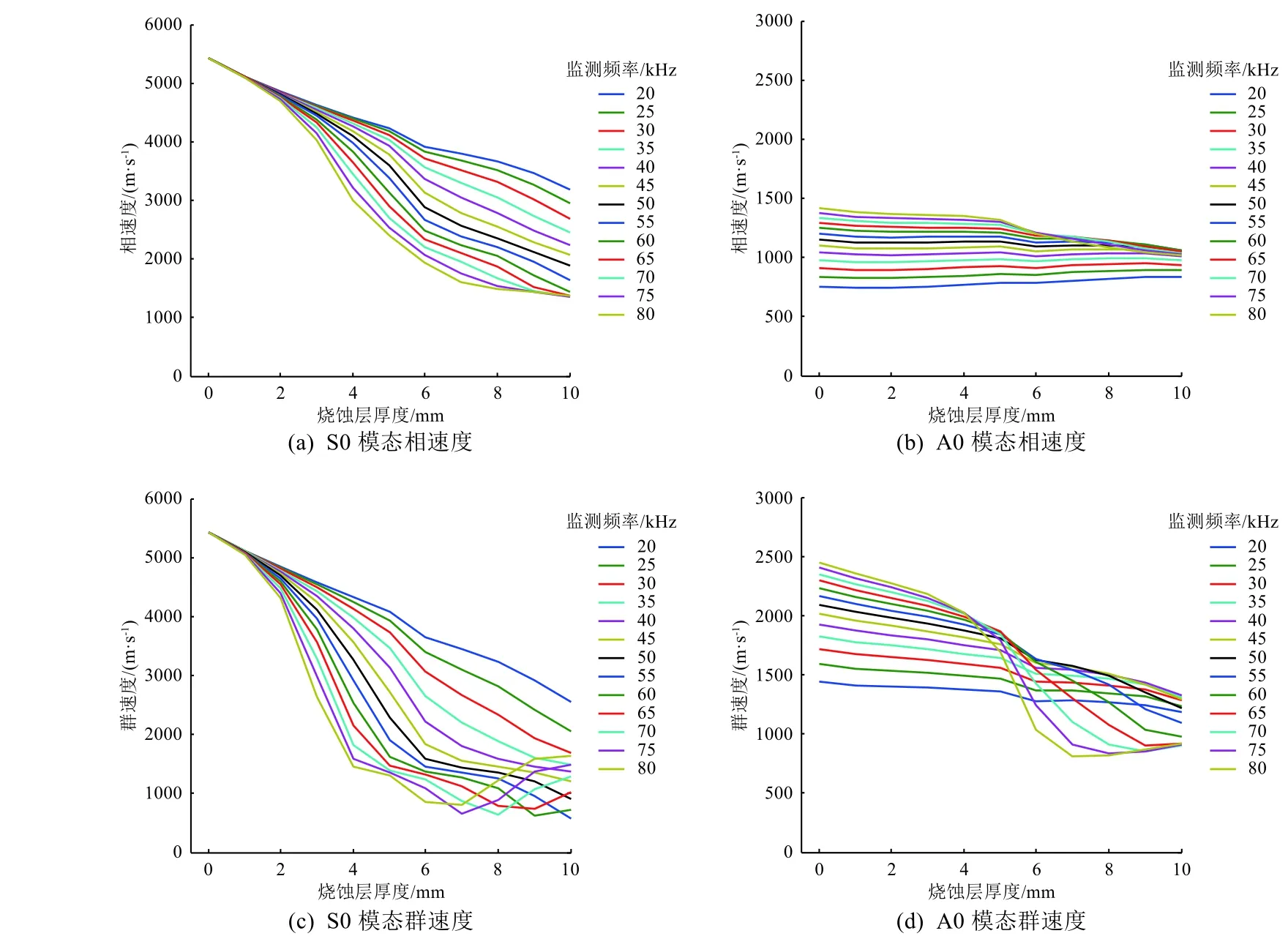
图 6 导波厚度敏感度曲线Fig. 6 The thickness sensitivity curve of guided waves

2.3 厚度特征提取方法

不同烧蚀层厚度下的理论相移计算公式为

式中：Cp0为无厚度损失下的导波相速度；Cp为监测的实时相速度；ΔCp=Cp-Cp0为相速度差；x0为导波激励端到接收点的距离。

由式(21)可以推导出相速度变化

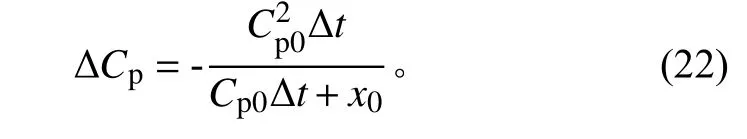
理论上，Cp0为由厚度损失的SAFE 计算得出的相速度；对于实验，Cp0可以通过不同路径的相位差来确定，

式中：x0和x1为2 条不同路径的导波传播距离；∆tx1-x0为这2 条路径导波信号的相位差。

因此，通过SAFE 计算理论相移拟合ΔCp与Δx0关系曲线，并依据该拟合曲线，由在实验过程中获取的导波信号对比于无厚度损失时的相移，即可获取烧蚀层厚度的变化。

2.4 有限元计算验证

为了对2.3 节所述的烧蚀层厚度监测方法进行可行性验证，本研究采用有限元软件进行了仿真模拟。图7 所示为双层复合结构中导波传播的二维有限元模型，双层结构材料分别设置为铝和E51。结构导波传播方向长度为1 m，铝层厚度为3 mm，E51 层厚度设置多个数值（0、1、2、3、4、5 mm）。

图 7 双层复合结构有限元导波传播模型Fig. 7 The FE model of guided wave propagation inside double layer plates

模型选取四节点双线性平面应力四边形单元（CPS4R），已有研究人员探讨了单元网格大小对导波有限元计算结果的影响，网格大小设置应遵循“每波长包含10～20 网格”的规则[20-21]。选取结构左端作为激励端，与接收点距离0.5 m，即导波传播距离。激励输入信号选取经汉宁窗调制的5 周期正弦信号，中心频率为40 kHz，接收到的导波信号如图8 所示。由图8 可以看出，随着E51 层厚度的增加，接收到的导波信号有明显的向后相位移动，即不同烧蚀层厚度下的导波信号之间有明显的相位差。

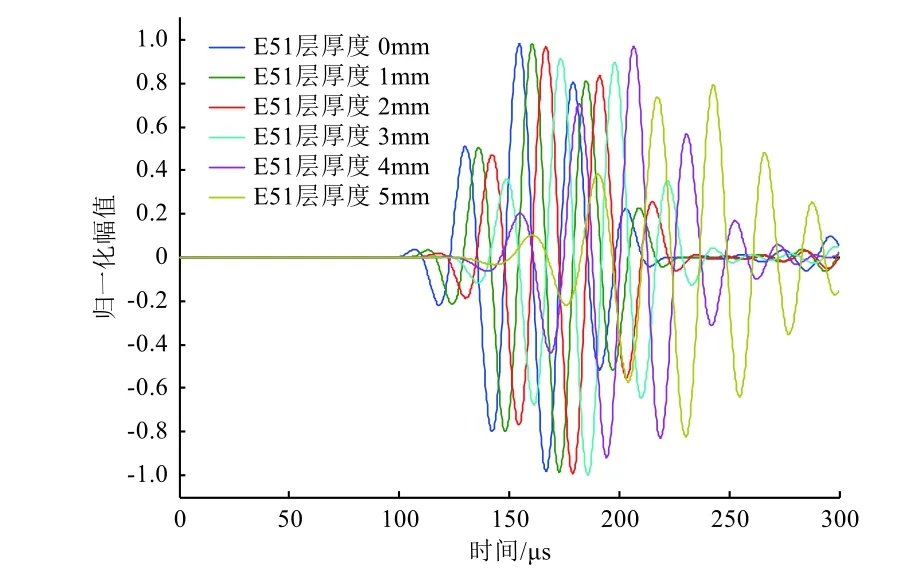
图 8 40 kHz 激励频率下有限元模拟导波时域信号Fig. 8 Time-domain FE simulation signals of guided waves at 40 kHz

选取5 周期信号最高峰前半个周期与0 值轴交点计算各导波信号间的相位差，进而计算得到导波相速度的变化值，40 kHz 激励频率下有限元模拟导波信号相速度随烧蚀层厚度的变化结果如图9所示。由其与SAFE 计算拟合曲线得到的导波信号相速度变化曲线对比可以看出，二者线性吻合度较好，变化规律基本一致。可以证明导波相速度随着烧蚀层厚度的增加而增大，即随着厚度缺失而减小，因此可以基于导波相速度的变化进行烧蚀层厚度监测。

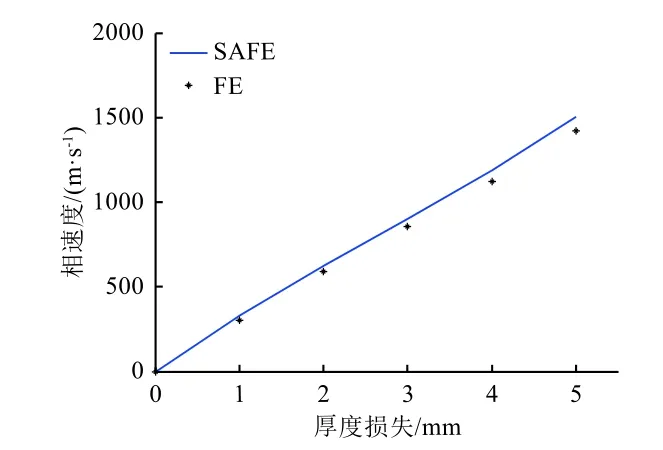
图 9 40 kHz 激励频率下有限元模拟导波信号相速度变化曲线Fig. 9 FE simulation results of different phase velocities of guided wave at 40 kHz

3 烧蚀层厚度监测实验

3.1 实验设置

本次实验选取的实验对象为铝/E51 双层复合板试件。其中铝板厚度为3 mm，E51 层厚度为5 mm，有效双层区域平面尺寸为350 mm×150 mm，如图10所示。试件铝板背面共布置6 个PZT 压电传感器，3 个激励传感器，3 个接收传感器，相隔0.32 m。

图 10 实验用双层复合板试件Fig. 10 The double-layer composite sample for the experiment

信号激励参数设置为：采样频率12 Mbit/s，采样点数6000；激励频率40 kHz，峰-峰值100 V。本次实验采用机械切削的方式来模拟烧蚀过程，用数控铣床将E51 层厚度自5 mm 逐渐减薄为0 mm，即Δx0依次递增为1.00、2.00、3.00、4.00、5.00 mm，分别在各烧蚀层厚度下进行导波数据采集。

3.2 实验结果与分析

图11 所示为40 kHz 激励下不同烧蚀层厚度下的导波信号，可以看出，随着烧蚀层厚度的变化有明显的相位移动。

受实验条件的限制，所用的信号为5 周期信号，信号频宽并不是半解析有限元计算时的单频，越接近中间位置的相移越接近单频结果，故取靠近中间的与0 值轴交点计算相移。

图 11 不同烧蚀层厚度下的40 kHz 导波时域信号Fig. 11 The time-domain signals of guided waves at 40 kHz with various thicknesses of ablation layer

图12 为40 kHz 激励频率下相速度的实验结果及其与SAFE 计算拟合结果、有限元模拟结果的对比，可以看出厚度变化与相速度基本呈线性关系，且随着厚度损失的增加相移不断增大。

图 12 40 kHz 激励频率下导波信号相速度变化曲线Fig. 12 Phase velocity of guided wave signal at 40 kHz

由监测得到的相移结果与拟合曲线差值得到导波信号实时监测的厚度损失结果，如表2 所示。可以看到，40 kHz 激励频率下厚度监测的最大误差为0.36 mm，平均误差0.18 mm，与有限元模拟结果的误差水平相当。

表 2 厚度损失监测结果Table 2 The monitoring results of lost thickness

4 结束语

本文介绍了一种基于超声导波的返回舱热防护结构烧蚀层厚度实时在线高灵敏度监测方法，用导波波速变化表征结构厚度损失，根据导波频散曲线和厚度敏感曲线选择适宜的监测模态和频率，实现烧蚀层厚度损失实时在线监测；并分别进行了有限元仿真和实验测量，验证了该监测方法的可行性。本文提出的烧蚀层厚度实时监测方法，可为返回舱结构热防护结构研究工作提供数据支撑，反馈结构的可靠性设计。