基于累计加电时间的小卫星正样研制阶段可靠性问题统计及筛选评估方法

王世清，常 静，陆文高，葛 宇，王晓耕

（航天东方红卫星有限公司，北京 100094）

0 引言

在批量化生产（持续改进）和可靠性物理老化的双重作用下[1]，多数产品的故障率在其全寿命周期内呈现浴盆曲线的变化特点。浴盆曲线在可靠性工程中占有非常重要的地位[2-6]，特别是在解释老炼对改进产品可靠性的合理性方面。在产品研制和使用的早期阶段，其故障率处于一个随时间迅速下降的阶段，该阶段叫做产品的早期寿命阶段。注重产品质量和可靠性的企业，一般都会在产品早期寿命阶段末期再进行产品交付。这样，产品的早期寿命阶段是在研制单位的测试、试验、筛选和老炼中度过的。产品质量控制的严格程度不同，产品交付点在浴盆曲线中的位置会有或前或后的差别：产品交付点越靠前，老炼成本越低，遗留问题越多，用户体验越差；产品交付点越靠后，遗留问题越少，用户体验越好，然老炼成本也越高；如果产品交付点过于靠后而进入使用寿命阶段，则会提前耗损其使用寿命。

卫星产品故障率变化也具有浴盆曲线的特点，正样研制阶段属于卫星浴盆曲线的早期寿命阶段。卫星在正样研制阶段开展测试和试验就是为了发现和剔除卫星上潜在的问题和缺陷，进而在改正问题和缺陷后，使卫星的故障率迅速降低到浴盆曲线的盆底，达到使用寿命阶段。但如何判断卫星故障率是否接近或达到盆底，则需要深入研究卫星在早期寿命阶段的故障率变化规律。

受限于样本量较小，国内对卫星产品早期寿命阶段的故障率变化规律研究一直缺乏足够的统计数据支持。然这一现状已随着我国小卫星技术和应用市场的迅猛发展而发生改变，2000 年至2017 年，我国总共发射290 颗卫星，其中180 颗为小卫星。截至2018 年10 月，中国空间技术研究院已经成功发射95 颗小卫星[7]，其中绝大部分是由航天东方红卫星有限公司（以下简称公司）研制的。根据公司的最新统计，截至2018 年10 月29 日，已累计发射入轨90 颗小卫星，在大量小卫星型号研制的背景下，公司积累了丰富的研制数据，研究小卫星早期寿命阶段故障率变化规律的条件已经具备。

本文对公司已发射小卫星型号在正样研制阶段出现的所有质量问题中由设备、系统故障引发的可靠性问题进行归纳总结，以期发现小卫星在正样研制阶段可靠性问题的分布规律，并根据规律对不同累计加电时间出厂型号的可靠性问题筛选率进行评估，进一步根据筛选率水平分别针对首发星和装备星给出建议的出厂累计加电时间。

1 小卫星正样可靠性问题分布规律研究

1.1 数据统计和整理

一般来说，一颗小卫星在正样研制阶段的主要工作和历程如表1 所示。

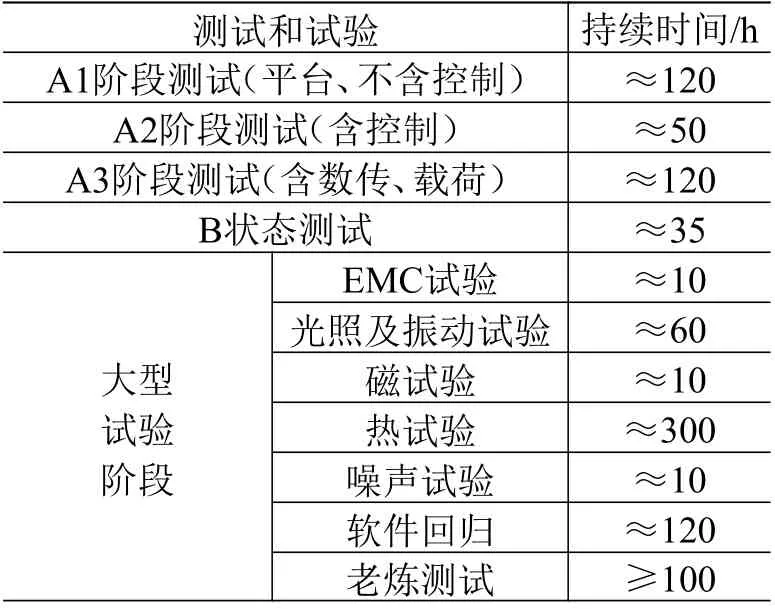
表 1 小卫星正样研制阶段的主要测试和试验Table 1 The main test and experiment in flight model phase of small satellites

截至2017 年12 月31 日，根据公司各型号已经上报的整星正样阶段加电测试期间出现的可靠性问题，可供作为分析依据的主要问题分属55 颗小卫星，所属平台相似度极高，可视为来自同一母体。其中去除原因不明、不可复现的问题，尚未完成归零、未查找出原因的问题，以及因为地面测试设备问题而导致的测试问题等非可靠性问题，共计220 个有效的可靠性问题，见表2。

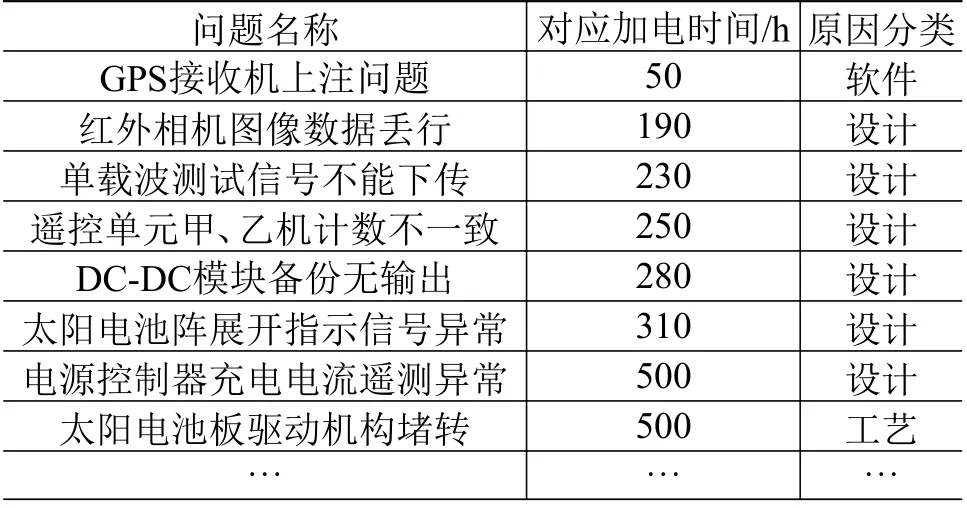
表 2 小卫星正样研制阶段可靠性问题统计（部分）Table 2 The reliability problem data of small satellites in flight model phase (only a part of data)

1.2 直方图分析

直方图是一种整理故障数据，找出其规律性的常用方法[8]。对表2 中所有型号正样研制阶段的可靠性问题按发生时间先后，进行排序和直方图分析，按照每100 h 进行分段，统计每个分段内发生可靠性问题的数量（即，第1 分段[0 h, 99 h)、第2 分段[100 h, 199 h)，以此类推），得出直方图如图1 所示。

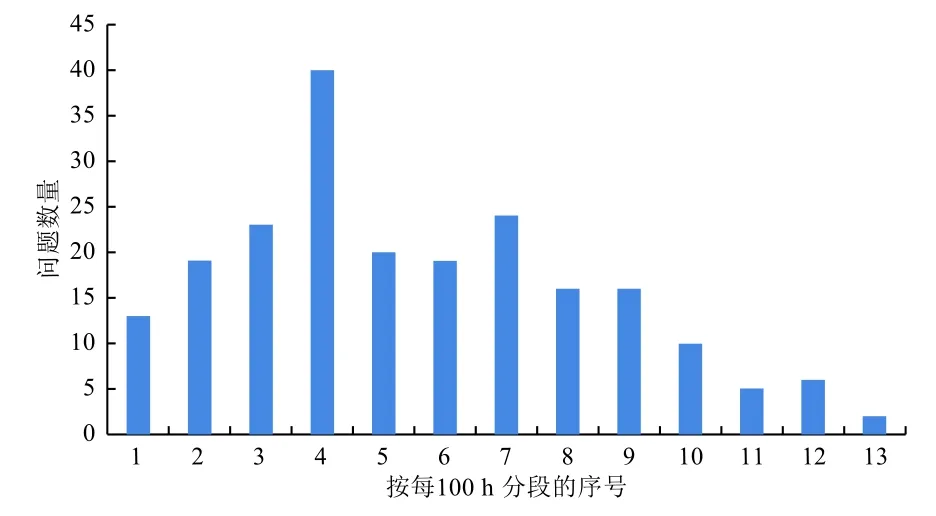
图 1 整星累计加电时间与可靠性问题数量关系直方图Fig. 1 Histogram of the number of reliability problems vs.accumulated power-on time

从图1 可以看出，小卫星型号在整星加电时间内的可靠性问题数量呈现较为明显的2 个波峰：第1 个波峰大概在[300 h, 400 h)，这时整星设备齐套，测试的项目最全，发现的问题也最多；第2 个波峰在700 h 左右，这时整星正在开展力学试验、热试验等加严条件的试验，通过施加加严的环境试验条件又激发出很多潜在的缺陷和问题。

1.3 分布模型假设

通过分析双波峰分布的形成机理，再根据小卫星加电测试的实际情况（不可能存在整星加电时间为负值），假设整星累计加电时间的可靠性问题分布是2 个对数正态分布的叠加，第1 个对数正态分布对应的是普通环境，从整星加电测试开始，峰值出现在350 h 左右；第2 个对数正态分布对应的是加严环境，从整星力学试验（根据统计，在整星累计加电约500 h）开始，经过热试验等，峰值出现在650 h 左右，分布模型如图2 所示。

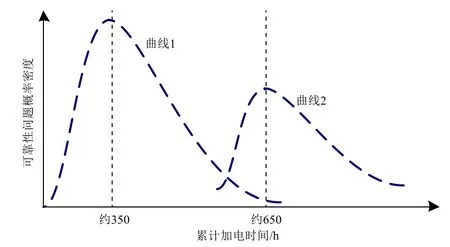
图 2 整星累计加电时间可靠性问题分布模型Fig. 2 The logarithmic normal distribution model of reliability problems according to accumulated poweron time

分布模型中曲线1 分布区间取[0, +∞)，曲线2分布区间取[500, +∞)，并假设：

1）小卫星整星加电测试期间可靠性问题的分布服从双对数正态分布（两参数）的叠加分布；

2）加严环境的对数正态分布起点为500 h，即从整星累计加电500 h 左右开始进行力学试验和热试验；

3）各可靠性问题相互为独立事件；

4）分布模型的概率密度函数f(t)和累积概率密度函数F(t)分别为[9-10]：

1.4 累积概率密度经验数据拟合和参数估计

将表2 中的经验数据整理成累积可靠性问题发生频率数据，然后采用MATLAB 软件辅助拟合，对CDF（累积概率密度）的拟合函数为

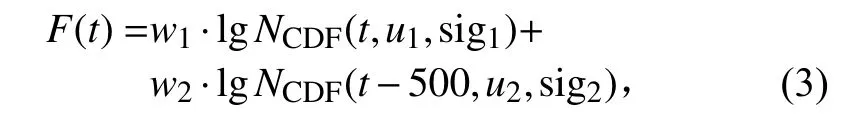
式中：t为加电时间；w1、w2为系数，介于0 和1 之间；u1、sig1和u2、sig2分别为2 个对数正态分布的均值和方差；lgNCDF(·)为MATLAB 中内置的对数正态分布的累积概率密度函数。通过MATLAB 软件优化拟合累积概率密度数据，计算6 个未知参数。

2 小卫星出厂累计加电时间建议

2.1 对首发星的研究和建议

通过对表2 中首发星型号的数据进行选择和整理，得到25 颗首发星共130 条有效的可靠性问题数据。采用1.4 节的方法对首发星的可靠性问题累积概率密度数据进行拟合，各参数拟合结果为：w1=1,w2=0.158 4,u1=6.209,u2=5.036, sig1=0.982 3,sig2=1.157；拟合优度0.995 1。

首发星的CDF 拟合曲线及其对应的PDF（概率密度）曲线分别如图3 和图4 所示。

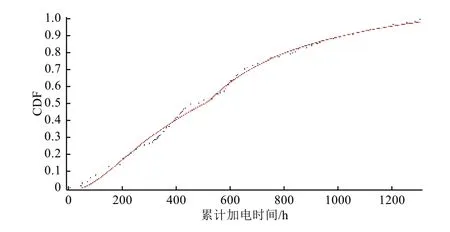
图 3 首发星整星加电时可靠性问题累积概率密度曲线Fig. 3 The fitted CDF curve of early reliability problems of the first-flight satellite

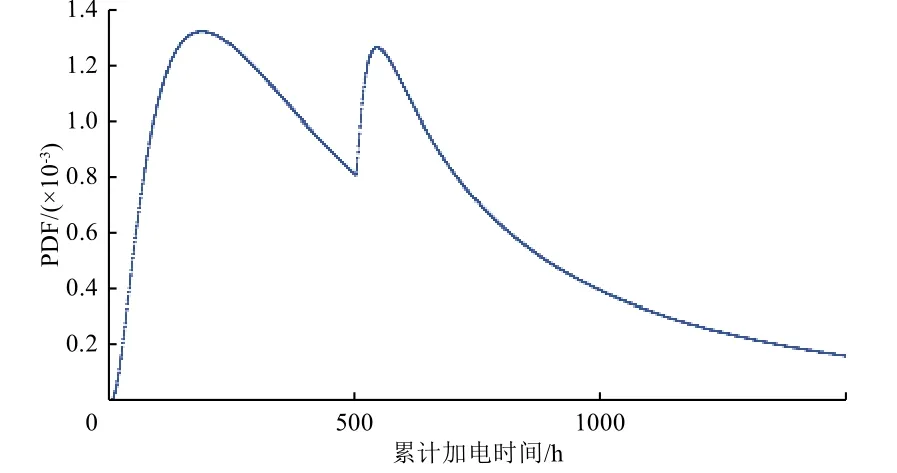
图 4 首发星整星加电时可靠性问题概率密度曲线Fig. 4 The fitted PDF curve of early reliability problems of the first-flight satellite

卫星的出厂可靠性问题筛选率，即出厂前已经发现的可靠性问题占卫星全部可靠性问题的比例，等同于累积概率密度F(t)，即

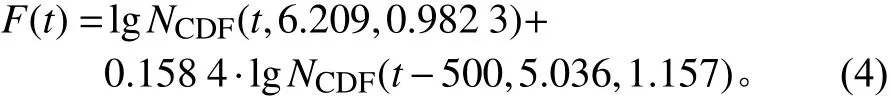
首发星典型累计加电时间出厂可靠性问题筛选率如表3 所示，结合传统的型号出厂要求（即累计加电时间≥1000 h），建议首发星的出厂时间为累计加电1040 h 以上，这样卫星出厂时的可靠性问题筛选率将＞90%。

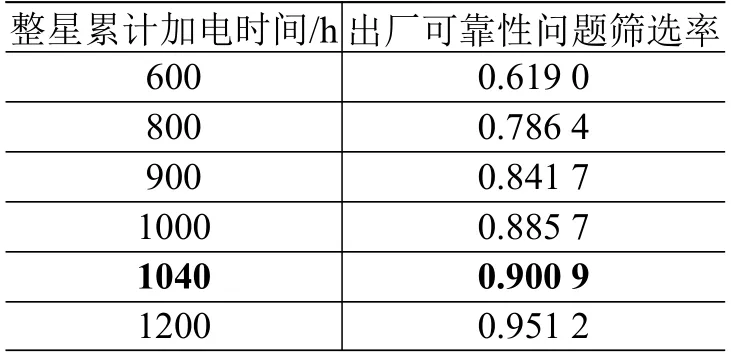
表 3 首发星典型累计加电时间与出厂可靠性问题筛选率Table 3 The screening rate of reliability problems at different accumulated power-on time of fist flight satellite

2.2 对装备星的研究和建议

通过对表2 中装备星型号的数据进行选择和整理，得到30 颗装备星共90 条有效的可靠性问题数据。采用1.4 节的方法对装备星的可靠性问题累积概率密度数据进行拟合，各参数拟合结果为：w1=0.851 1,w2=0.196 7,u1=5.925,u2=5.599, sig1=0.716, sig2=0.303 8；拟合优度0.993 3。

装备星的CDF 拟合曲线及其对应的PDF 曲线分别如图5 和图6 所示。

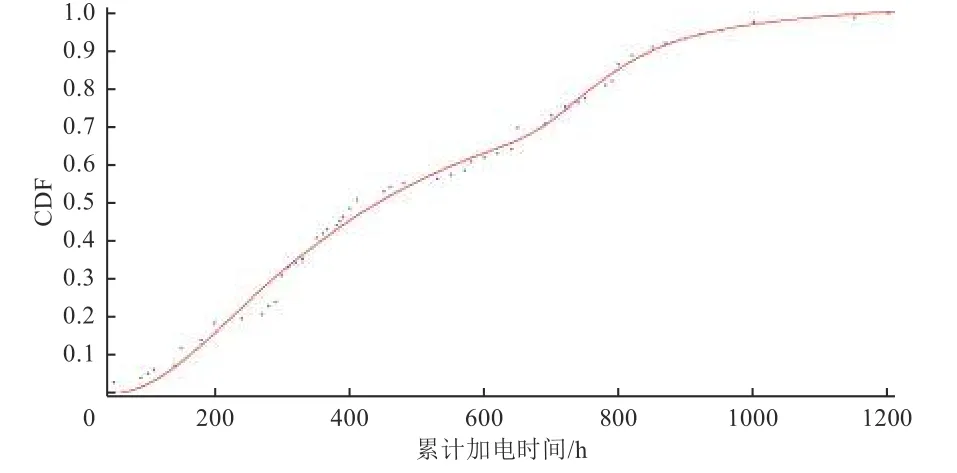
图 5 装备星整星加电时可靠性问题累积概率密度曲线Fig. 5 The fitted CDF curve of reliability problems of subsequent satellite

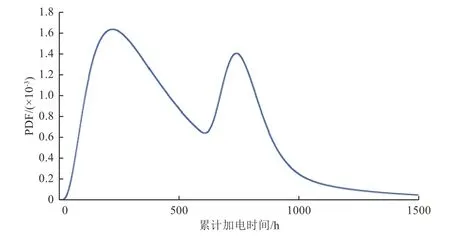
图 6 装备星整星加电时可靠性问题概率密度曲线Fig. 6 The fitted PDF curve of reliability problems of subsequent satellite

卫星的出厂可靠性问题筛选率等同于累积概率密度F(t)，即

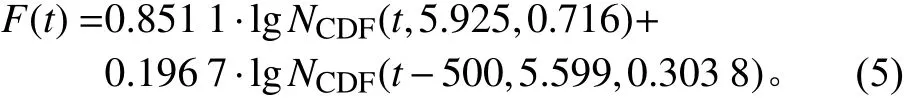
装备星典型累计加电时间出厂可靠性问题筛选率如表4 所示，建议装备星的出厂时间为850 h以上，这样卫星出厂时的可靠性问题筛选率将＞90%。可见，装备星较首发星的出厂累计加电时间缩短了近200 h。

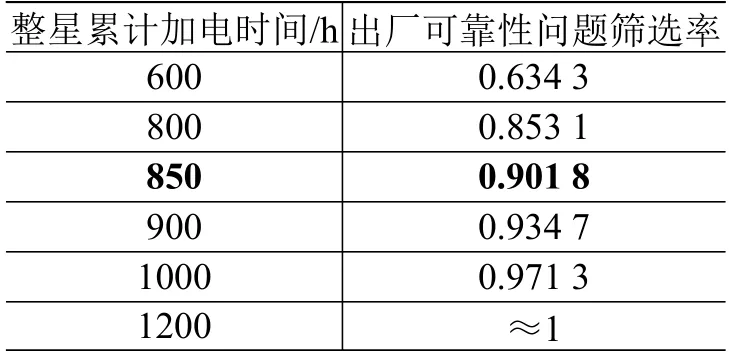
表 4 装备星典型累计加电时间出厂可靠性问题筛选率Table 4 The screening rate for reliability problems against different accumulated power-on time of subsequent satellite

2.3 初步建议

通过以上分析可以看出：

1）截至目前，已发射的小卫星型号都是按照1000 h 累计加电时间要求完成正样阶段测试和试验的，且在轨表现良好；而1000 h 累计加电时间对应的首发星可靠性问题筛选率为88.57%，因此可以就近取整将“正样可靠性问题筛选率＞90%即可出厂”作为小卫星出厂时间的确定依据。

2）按照目前的标准研制流程，同样的累计加电时间，小卫星装备星的可靠性问题筛选率要比首发星的高，如果将“正样可靠性问题筛选率＞90%即可出厂”作为依据，那么在完成规定的测试和试验项目情况下，首发星至少须满足整星累计加电时间超过1040 h 才能出厂，而装备星只需要整星累计加电时间超过850 h 即可出厂。

3）在小卫星整星加电测试可靠性问题的分布曲线中，第2 个波峰是由加严环境（整星力学试验和热试验）诱发的，其出现位置可以通过改变整星大型试验的开始时间予以调整。为了节省研制时间，尽早出厂，在型号（尤其是装备星）研制过程中应该尽早开展整星的力学试验和热试验，最理想的情况是能够将第2 个波峰隐藏到第1 个波峰下。也就是说，通过合理安排整星力学试验和热试验的开始时间，整星的出厂累计加电时间可以进一步缩短。

3 结束语

本文针对航天东方红卫星有限公司已经发射入轨的小卫星型号在正样研制阶段内出现的大部分可靠性问题进行了统计分析，研究了小卫星浴盆曲线早期寿命阶段的规律：

1）发现了小卫星正样阶段整星可靠性问题分布具有双波峰的特点；

2）提出的双对数正态叠加分布模型能很好地描述小卫星正样可靠性问题分布规律，在首发星和装备星的经验数据分析中拟合优度均大于0.99；

3）给出了小卫星整星可靠性问题的分布经验公式和分布曲线；

4）给出了小卫星出厂可靠性问题筛选率评估方法，并分别针对首发星和装备星给出了建议的出厂整星累计加电时间。

随着我国研制的小卫星总量逐步增加，积累的研制数据也会越来越丰富，应当及时对这些数据进行挖掘分析，发现数据背后的工程研制规律，进而更好地指导研制工作的开展。

对于复合型分布模型的假设检验，本文尚未找到有效方法，因此文中仅对拟合优度进行了计算，未对双对数正态叠加分布进行假设检验，希望通过后续进一步深入研究予以解决。