第一性原理在固体物理晶体结构教学中的应用
于 洋
(南京信息工程大学 物理与光电工程学院,江苏 南京 210044)
由于原子间的结合力,使固体原子趋于紧密排列,常见由单元素构成的固体如金属,具有简单的晶体结构[1-3]. 典型的金属晶体结构有4种:简单立方(sc)、体心立方(bcc)、面心立方(fcc)以及六方密堆积(hcp). 由固体物理可知,材料结构趋向于能量最低的稳定状态,晶体结构由于对称性,原子间距离最近、密度最大. 按致密度,面心立方和六方密堆积最高为0.74,bcc次之为0.68,sc最低为0.524. 若只考虑几何因素,对于各向同性原子构成的固体,致密度越高,原子间距离越近,体系能量越低. 最外层电子为满壳层结构的稀有气体在高压低温下就是以致密度最高的六方密堆积(如He)和面心立方(如Ne、Ar、Kr和Xe)晶体形式形成固体结构. 但实际金属固体并非全为致密度最高晶型,例如钨为体心立方,钋为简单立方,说明除几何结构的最密集排列因素,原子内部的电子结构也对原子间结合的能量具有影响. 而对于电子结构的影响,几何方法及经典力学无能为力,只有引入量子力学方法才能解决. 第一性原理计算方法根据量子力学原理计算材料的电子结构,获得精确的固体原子电子结构信息,可以计算任意假想晶格结构总能. 本文利用密度泛函理论[4,5]结合第一性原理软件(Quantum Espresso)[6,7]对钋、钨、铝和镁等金属晶体进行模拟,计算其在不同晶体结构下随晶格常数变化的能量曲线,讨论各金属晶体的理论晶格结构,并与实验结果进行对比,从理论角度解释为何不同金属呈现不同晶体类型.
1 计算方法与模型
采用密度泛函理论(DFT)框架下的PBE[8]泛函,利用第一性原理软件(Quantum Espresso)进行计算. 使用SSSP赝势[9,10]描述离子实与价电子之间的相互作用. 布里渊区K点取样13×13×13,体系截断能100 Ry (1 361 eV).
本文模拟的4种金属钋、钨、镁和铝均建立4种晶格类型,即简单立方、体心立方、面心立方和六方密堆积,4种晶格类型的晶胞模型如图1所示. 晶胞常数在2~10 Å之间以0.1~0.5 Å间隔变化,计算在每一个晶胞常数下的单点能. 能量结果以单个原子平均能量值表示,单位为eV,并以原子间隔无穷远作为能量为零的标度.
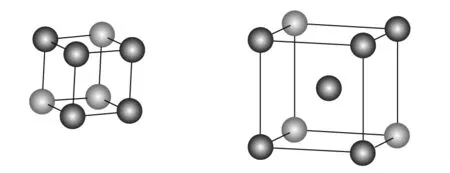
简单立方(sc) 体心立方(bcc)
2 金属晶体理论晶格结构
通过第一性原理计算4种金属钋、钨、铝和镁在4种晶格(简单立方、体心立方、面心立方和六方密堆积)中晶格能量随晶格常数的变化,结果如图2所示. 每种金属随4种晶格的能量变化趋势相同,所有晶体结构,其体系能量随晶格常数变化均有一个最低值,能量最低值对应的晶格常数称为平衡晶格常数. 当晶格常数小于此平衡晶格常数时,晶格常数变小时能量逐渐增加;当晶格常数大于此平衡晶格常数,晶格常数变大时能量逐渐增加. 但4种金属在不同晶格类型下对应的最低能量不同,此最低能量对应的晶格类型即根据第一性原理计算出的该金属所呈现的理论晶体类型.
如图2(a)所示,Po金属在4种晶格结构下均有能量最小值,面心立方能量最低值是 -2.526 eV;体心立方能量最低值为 -2.606 eV;六方密堆积能量最低值为 -2.725 eV;简单立方能量最低值为 -2.857 eV,显然简单立方的能量最低值是4种晶格类型能量最低值中的最小值. 能量越低,体系越稳定,因此,理论上来说,钋金属固体应该呈现的晶型为简单立方. 计算所得钋金属简单立方结构对应的平衡晶格常数为3.33 Å. 由图2(b)可以看出,钨金属在体心立方结构下能量最低值是4种晶型中的最小值,体心立方对应的平衡晶格常数为3.18 Å;由图2(c),铝金属对应的理论晶格类型是面心立方结构,计算所得平衡晶格常数为4.05 Å;由图2(d),镁金属对应的理论晶格类型是六方密堆积结构,计算所得平衡晶格常数为a/c=3.28 Å/5.41 Å. 以上结果总结在表1中. 本文计算获得的理论晶格类型及平衡晶格常数结果与实验结果相符[11].
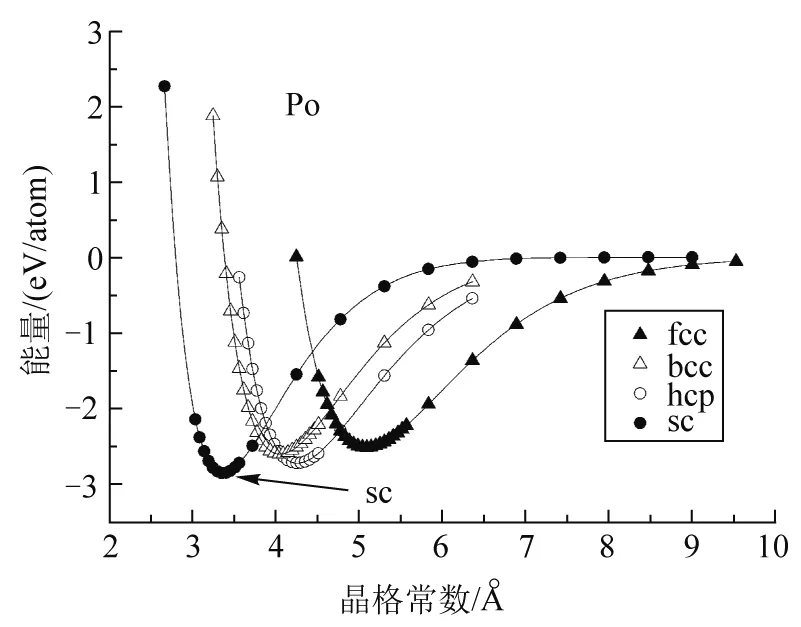
钋

表1 根据第一性原理计算获得的晶格类型及平衡晶格常数
3 总结
本文基于第一性原理,计算了钋、钨、铝和镁金属在各种晶格类型中随晶格变化的能量,决定最终晶格结构的是能量,能量越低,体系越稳定,理论上金属固体以能量最低晶格类型排列[12]. 几何结构是影响凝聚态物质能量的重要因素,高对称、最密集排列的晶格结构如面心立方、六方密堆积具有最低能量,因此很多晶体呈面心立方和六方密堆积晶体结构. 但几何因素不是唯一因素,原子的电子结构也是重要影响因素,本文利用第一性原理软件Quantum Espresso计算获得的金属理论晶格结构和平衡晶格常数结果与实际晶体数据相符,证明量子力学的重要性以及量子力学在固体物理学习中的重要地位.

