应用质点系的动量定理求解柔软链条的运动

邵 云

(南京晓庄学院 电子工程学院，江苏 南京 211171)

本文将应用质点系的动量定理详细地求解出3类柔软链条的运动，一则显示出该方法的优势[1-4]，二则揭示出这3种运动各自的细节特点，以供读者参考．

1 光滑桌面上一团静止柔软链条的逐节下落运动

例1：如图1所示，有一段柔软的链条长为l，单位长度的质量为λ，被放置在有一小孔的光滑桌面上．设开始时(t=0)链条一端由小孔稍稍伸下，其余部分堆在小孔周围.现由于某种扰动，链条因自身重量开始下落，试求链条下落的速度与距离的关系．

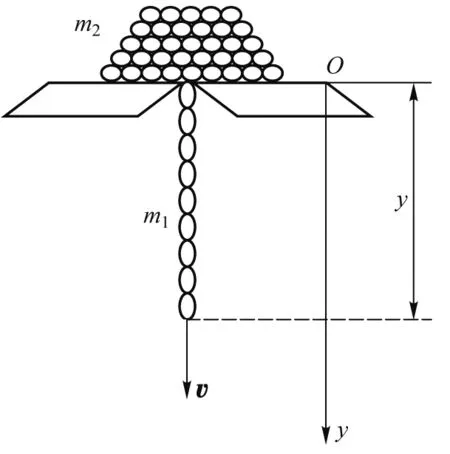
图1 一团静止柔软链条的逐节下落运动

解析：建立Oy坐标轴如图1中所示．设上、下两段链条的质量分别为m2和m1，并设t时刻下段链条的长度为y，速度为v，则在t时刻，有

m2=λ(l-y)

(1)

m1=λy

(2)

设上段链条不包括小孔口开始运动的那一小节，则它处于受力平衡状态．现将上、下两段链条视为一个系统，则不难看出，系统在竖直方向所受的合外力为FG1=m1g，总动量为m1v．于是，根据质点系的动量定理，则有

(3)

将式(2)代入式(3)，约简后在图1中y轴正方向进行投影，则得分量方程为

(4)

再将式(4)两边同乘以ydy，得

(5)

(6)

其中已将yv整体视作一变量．式(6)经计算整理后即得

(7)

此即链条下落的速度与距离的关系式．

将式(7)两边分别对时间t求导，再利用式(7)本身便得

(8)

可见下落段链条的实际运动是一个加速度为g/3的匀加速直线运动．

2 光滑桌面上柔软直链条沿桌边逐节下滑的运动

例2：如图2所示，有一段柔软的链条长为l，单位长度的质量为λ，被拉直放置在一光滑的桌面上．设开始时(t=0)链条的一端稍稍伸出桌子边缘，现由于某种扰动，链条因自身重量开始下落，试求链条下落的速度与距离的关系．(注：不考虑链条在桌子边缘的离心运动[3]).

图2 柔软直链条沿桌边的逐节下滑运动

解析：对于如本例这种链状质点系沿固定切向(τ)的约束运动，其上任意质点mi沿切向的动力学方程可以写成

(9)

(10)

式(10)可称为“链状质点系沿切向运动的动力学方程”．

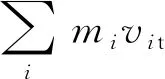
(11)

将式(11)两边同乘以dy并整理得

(12)

再结合初始条件，对式(12)两边进行定积分得

(13)

解得

(14)

此即链条下落的速度v随距离y的变化关系．易见链条下落的加速度为

(15)

这表明链条在做一加速度随距离(或位移)均匀递增的变加速直线运动，当链条完全脱离桌面时，加速度达到最大值g．

3 恒力逐节竖直拉起一大团静止柔软细链条的运动

3.1 问题的提出及初步的研究

例3：如图3所示，有一大团柔软的细链条叠放在水平地面上，单位长度质量为λ．现以恒力F将链条一端竖直提起，试求链条接下来的运动．

图3 恒力逐节拉起一大团静止柔软细链条的运动

解析：将整段链条视为一个系统，因地面静止链条部分处在瞬间平衡状态，故系统所受合外力为F+λyg，系统的总动量为λyv．于是，根据质点系的动量定理，沿图3中y轴正方向有

(16)

根据初始条件对式(16)进行积分可解得

(17)

此即链条在首次(其后会有反复振荡)上升过程中的速度v上1与位移y的关系．将式(17)对时间t求导并利用式(17)本身，便得加速度:

(18)

可见链条在首次上升过程中做一加速度为-g/3的匀减速直线运动．

从式(17)又可见，当链条上升的速度v上1=0,也即

(19)

时，链条上升至第一个最高点．此外，由式(16)结合式(17)或式(18)可得

(20)

对比式(16)、(20)可以发现，上升段链条的静力平衡点处在

(21)

处，此处yv达到极大值，将式(21)代入式(17)即得此极大值为

(22)

当链条首次到达最高点后开始下落时，式(16)将不再成立．这是因为瞬间落地的极小段链条会对地面有一个类似于上文“拖拽力”的变质量冲力λv2，因而地面对链条的支持力也将额外增加λv2，式(16)需要修改成

(23)

(24)

(25)

它迥然不同于首次上升时的加速度-g/3．

根据首次下落过程的初始条件，从式(25)积分可得链条首次下落时的速度与位置的关系为

(26)

将式(19)代入式(26)即得

(27)

令式(27)中的v下1=0，即可数值解得链条(端点)首次下落的最低点坐标为

(28)

(29)

3.2 链条的第2次振荡

对于链条的第二次上升过程，在考虑到相应的初始条件后，对式(16)进行变换并积分可得

(30)

由此解得链条第二次上升的速度为

(31)

联立式(16)、(31)即求得加速度为

(32)

令式(31)中的v上2=0，即解得链条第二次上升的最大高度为

(33)

(34)

将式(34)代回式(31)，即求得链条第二次上升时的最大速度为

(35)

不难验证，若令式(31)—(35)中的y1min→0，则它们将还原成上文首次上升时的结果．

对于链条的第二次下落过程，由于其动力学方程依然服从式(25)，因此下落速度与位置的关系应与式(26)类似，为

(36)

(37)

3.3 链条运动的完整描述

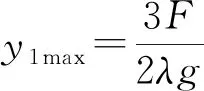
(38)

(39)

式(38)、(39)分别是以第n+1次上升、下落运动的起点为计时起点的，它们都是隐函数形式的运动学方程，且都是积分方程，需要数值计算．因此，要获得链条完整的运动学方程是颇费周折的．

(40)

(41)

诸参量的具体数据详见表1，其中均选择了归一化的单位．根据表1，可作出链条振荡的最低点和最高点坐标随时间的变化图4，以及链条在各段振荡过程中的最大速度变化图5．图4中的时间t为累计时间．

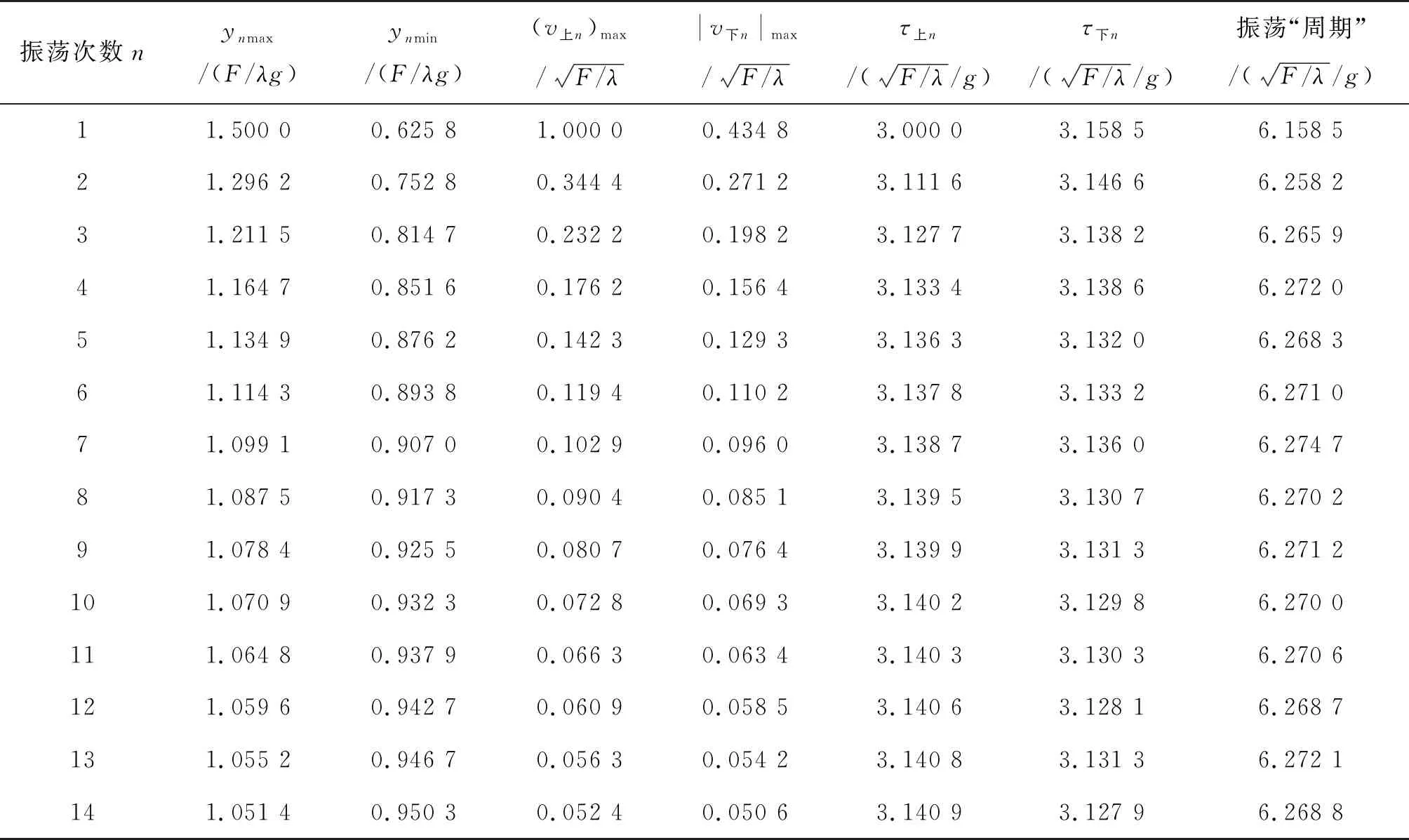
表1 链条各次振荡的几个主要的运动状态参量

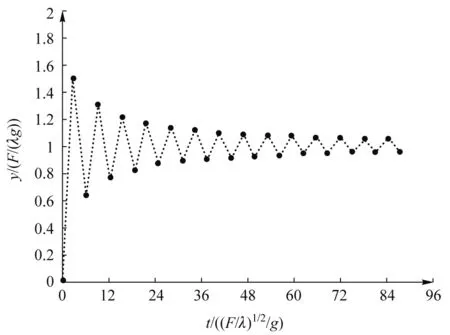
图4 链条振荡的最低点和最高点坐标随时间的变化

图5 链条在各段振荡过程中的最大速度变化情况

4 总结与说明

本文通过3个典型的例题，阐述了应用质点系的动量定理来求解柔软链条运动的具体方法．从结果看，该方法物理思想凸出，计算过程也较为简洁．

从加速度的观点看，光滑桌面上一团静止柔软链条的逐节下落运动是一个加速度为g/3的匀加速直线运动；光滑桌面上柔软直链条沿桌边逐节下滑的运动则是一个加速度随位移均匀递增的变加速运动；而恒力逐节竖直拉起一大团静止柔软细链条的运动则是一个振幅不断衰减的上下振荡，其中上、下运动的动力学方程存在差别，导致链条的上、下振荡并不对称，无论幅度、时间还是最大速度等，参见表1．本文第3节又显示，在同一次上下振荡中，链条上升的幅度和最大速度分别总是大于下降的幅度和最大速度，但是上升和下落的时间τ上n与τ下n在变化趋势上恰相反，两者之间存在着一个等值的交汇点(见表1)；不过，τ上n与τ下n之和即所谓的振荡“周期”，除首次振荡外却几乎是一常量，这就意味着链条几乎在做等“周期”的振荡．

本文的式(31)—式(37)都是通用的表达式，它们对包括首次在内的任意一次振荡皆适用．因此本文第3节能够运用Excel软件，通过迭代的方法求出各次振荡的主要特征参量，以此呈现该链条大致的振荡图像．再次声明，由于从隐函数形式的运动方程式(38)、(39)数值积分，分别求出第n+1次上升、下落运动的y-t曲线，再逐段合并拼得链条完整的y-t曲线，这其中的程序颇为繁琐复杂，因此本文省略了该项工作，转而采用运动特征参量来描述该链条的振荡运动，如此或可使其运动特征更加鲜明．

最后，顺便说一下，与例1、3不同，例2中链条的各节之间不存在非弹性碰撞，因此其系统的机械能是守恒的．此外，例2中所推导采用的“链状质点系沿切向运动的动力学方程”式(10)，其实是切向的自然坐标轴上牛顿第二定律分量式的必然结果，事实上它在基础力学的实际教学中经常被采用[3]，并非罕见．