考虑节点负载的多社团网络级联失效问题研究
任林涛,裴忠民,熊 伟,罗章凯
航天工程大学 复杂电子系统仿真重点实验室,北京 101416
近些年来,针对复杂网络级联失效问题,许多专家学者在各个领域开展了大量研究[1-4]。Motter等人[5]最先提出了一种基于介数定义节点初始负载的线性负载—容量(ML模型),得出网络介数分布的差异性导致攻击介数高的节点越容易导致级联失效现象发生。段东立等人[6]针对的负载重分配规则是介于全局分配与最近邻分配、均匀分配与极端非均匀分配的特点,提出了一种可调负载重分配范围与负载重分配异质性的级联失效模型。唐亮等人[7]考虑节点具有恢复和重复失效等特征,构建了故障节点概率传播模式下的级联失效模型。郝羽成等人[8]针对现实网络中节点对负载的冗余能力,提出一种考虑节点过载状态的复杂网络级联失效模型。Tian等人[9]根据控制节点在内的相依网络之间节点负载依赖关系,提出了一种在相依网络上基于节点负荷的级联故障模型。
以上文献都是从均匀网络、无标度网络结构或相依网络等方向研究级联失效问题,没有考虑社团结构[10]对级联失效作用的影响,而社团结构作为复杂网络最普遍和最重要的拓扑结构属性之一,广泛存在于现实生活中[11-13],其结构特征表现为社团内部节点连接紧密,社团间节点连接比较稀疏。研究社团网络级联失效问题,能更好地从社团网络结构特征出发理解产生级联失效的原因,对寻找提升网络鲁棒性方法有非常重要的意义。
Wu等人[14]采用节点度定义节点初始负荷,研究了具有社团结构的无标度网络抗毁性,结论表明社团结构越明显其越具有鲁棒性。李浩敏等人[15]研究了多社团结构网络的级联失效问题,得出网络的拓扑结构参数变化会影响网络的抗毁性,但没有具体研究不同攻击策略对级联失效的影响;陆靖桥等人[16]在经典的线性负载容量模型基础上,有选择地对社团边界节点的容量附加二次容忍值,建立级联故障抵制模型,但只选取了固定结构的电力社团网络作为研究对象,没有推广到一般性质的社团网络。
本文设计一种社团规模和社团结构可调的网络结构模型,以节点度和介数共同定义节点初始负载,根据社团结构特征,对头节点附加二次容忍负载,采用局部相邻节点分配策略处理失效节点负载,提出初始负载、容忍负载、临界负载三个阶段节点失效模型。通过仿真分析了节点在遭受随机攻击和蓄意攻击时,节点负载模型参数和多社团网络结构对网络鲁棒性和级联失效作用的影响。
1 多社团网络生成模型
本文在文献[17]的基础上,提出一种社团规模和结构可调的多社团网络模型,生成方法如下:
(1)初始网络:设初始网络有M个社团,将社团标记为C1,C2,…,CM。每个初始社团都是由m0(3≤m0)个节点组成的全连接网络(当m0最小值为1和2时初始网络无法区分出有效的社团结构)。同时为确保初始社团间的连通性(不产生孤立节点和孤立社团),设任意两个社团间均有一条社团间连接边。
(2)节点增长:在每一个时间间隔内新加入一个节点(也可以每一个时间间隔加入多个节点),新增加的节点则以概率ph进入社团Ch,则有当新增加节点确定进入社团Ch后,则需要选择连接此社团内部m(1 ≤m≤m0)个节点,此时,新增加节点与Ch社团内的节点j相连的概率取决于节点j在Ch社团内度dhj所占本社团所有节点度的比例,即:

同时,新增加的节点以概率β进行社团间的连接(通过设置概率β可以控制社团间连边的数量,进而调整多社团网络的网络结构)。文献[17]中新增加节点与其他社团节点进行n次连边操作,每一次连边操作前都要依概率pt选择连边的社团Ct(t≠h),再依照节点度分布的比例选择社团Ct内某个节点进行连接;而本文则是先依概率pt选择连边的社团Ct,再在社团Ct内挑选n个不同节点进行连边操作。这n个节点的选择同样取决于其占Ct社团所有节点度的比例,比例越大,越容易被选择。通过上述与文献[17]社团间连接的建模过程对比可以看出,本文建模的复杂度要相应低一些,而且n越大,复杂度差异就会变得更大。
以上多社团网络的建模过程可以通过调节新节点加入社团的概率ph(h=1,2,…,M)来控制每个社团的规模。当ph=1/M时,即新节点进入每个社团的概率都相等,这样最终生成的多社团网络中每个社团的节点数量几乎相等,此时生成的网络就是均匀的,反之网络就是非均匀的。另外,新节点进行社团间连接时,挑选连接社团时也是以概率ph(h=1,2,…,M)进行选择的,也就是说某个社团节点数越多,越能吸引新节点加入。同时,与文献[17]相比,本文在一个社团内挑选n个不同节点进行连边,这样更容易使节点数多的社团产生更多的社团间连接,而且规模越大且社团间连边数越多的社团节点,越容易吸引其他社团节点与其进行连接。这样的情形在真实网络中较为常见,比如实力强的团队越能吸引新人加入,同时还能加强与其他实力较强团队的合作,实现强强联合,这也说明了本文生成的多社团网络更具一般性,与实际网络更吻合。
设M=3,m=2,m0=3,p1=1/6,p2=1/3,p3=1/2,β=0.1,n=1,N=200。生成的多社团网络拓扑图和多社团网络邻接矩阵图如图1和图2所示。
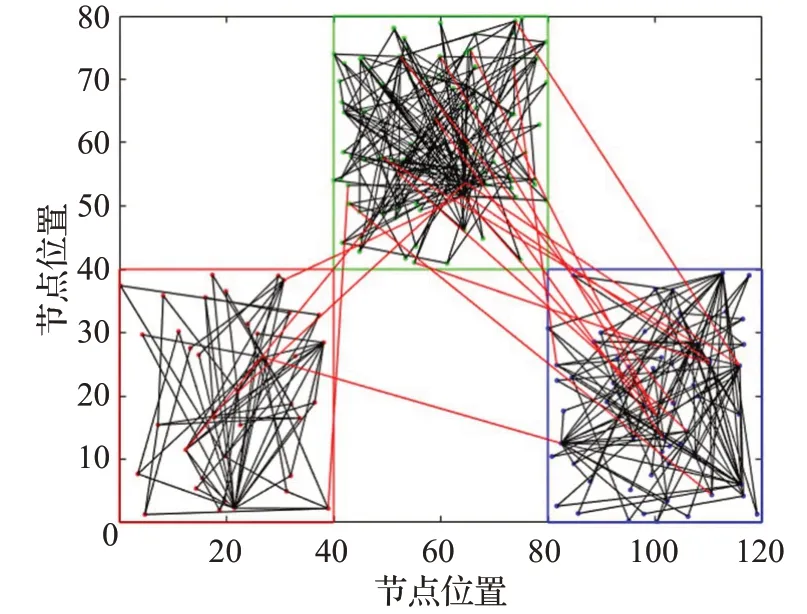
图1 多社团网络拓扑结构图Fig.1 Multi-community network topology diagram
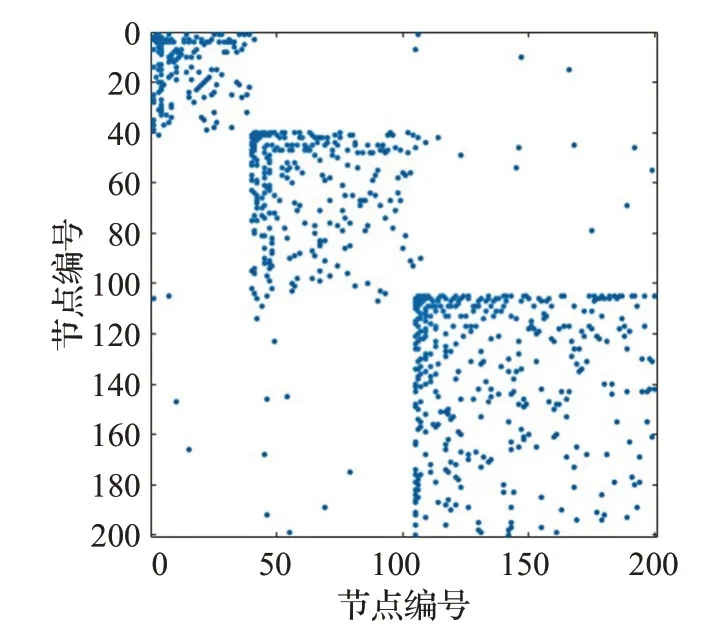
图2 多社团网络邻接矩阵图Fig.2 Multi-community network adjacency matrix
根据上述参数设置,取100次仿真结果平均值,得出多社团网络拓扑结构参数如表1所示。
从表1得出,生成的多社团网络平均路径长度和网络直径与真实多社团网络相比较小,具有“小世界效应”[18],模块度为0.56,说明网络的社团化特征明显[19]。同时,生成网络头节点个数占节点总数的比例为17.9%,产生的社团间连接数比社团内部连接数小得多。

表1 多社团网络拓扑结构参数Table 1 Multi-community network topology parameters
2 节点负载评估模型
2.1 节点负载相关定义
Motter等人提出的ML模型中,定义节点i的容量C(i)与初始负载l(i)存在线性关系,即C(i)=(1+α)l(i),α表示为容量调节参数。这种定义由于简单通用性强而被大多数学者所采用。但是随着研究的不断深入,Kim等人[20]通过研究电力网、航空网、交通网等现实中的网络,发现网络中具有较小负载的节点反而拥有较大的空闲容量,即在大多数网络中,节点的容量与负载并非呈简单的线性关系。为体现这种非线性关系,陆靖桥、丁超等人[21]以及其他许多学者在其研究中都相应地给初始负载l(i)中添加了指数调节参数,来控制初始负载的强度。
在描述节点属性的参数中,节点度、介数[10]是其中最重要的两个。由前文生成的多社团网络的静态参数可知,网络中只有少部分节点度具有较高的值,大部分节点度值都比较小,因此只选用度作为节点负载区分度不高。从全局刻画节点重要性的另一个重要指标是介数,但本文经过仿真后发现有个别节点的介数为0,这是因为这些节点都是处于整个网络的边缘,其他节点之间的最短路径都不经过这些节点,因此本文选择用度和介数共同来定义节点的初始负载参数,本文将节点的初始负载定义为:

d(i)为第i个节点的度,B(i)为第i个节点的介数,a、b分别为节点度和介数的倍数参数。由于节点度在数值上远小于节点的介数,为了使度和介数能够调整到同一数量级,使得能用度和介数共同反映节点初始负载,本文用θ作为节点介数的指数调节参数。
头节点作为多社团网络节点之间交互的枢纽,是保持网络结构完整性最重要的节点,因此在社团内节点的负载保持不变的情况下,可以通过对头节点附加二次容忍负载值,来研究头节点对网络结构的影响。

Γm为节点i与其他社团头节点连接的集合。表示与节点i连接的其他社团头节点初始负载之和。p为附加的二次负载调节参数,且0≤p≤1。节点若该节点不是头节点时,p=0,W(i)退化为ML模型。
对于复杂网络中的节点而言,本身就具有正常运行时能够承受的负载,假定在节点承受负载范围内运行就不会失效,本文将这个不会发生失效的负载上限定义为容忍负载R。

λ为节点容忍负载系数,λ≥0。
在诸多实际网络中,节点超过容忍负载运行时,一般都不会立即失效,反而能在此状态下维持一段时间,此时人们会采取多种措施确保整个网络能够正常运转,若是采取措施不及时或者节点一直在容忍负载高位运行,就有可能导致节点失效,本文把节点失效的阈值称为临界负载L。

式中,k表示临界负载系数,k≥0。
2.2 失效节点负载重分配策略和流程
失效节点负载重分配策略可以分为两类[22]:一种是基于全局搜索的分配策略,这种策略计算复杂度高,需要大量时间进行遍历;另一种是基于局部搜索的策略,这种分配策略是将失效节点的负荷按照一定的规则分配给与失效节点相连的节点,该方法计算复杂度低。作为社团网络,节点在社团内部连接紧密,在社团间节点连接稀疏,失效节点负载大概率分配给同社团的其他节点,因此本文采用负载局部重分配策略。
当一个社团网失效节点数量超过一定比例时,失效节点的负载才开始向其他社团的节点进行分配,本文将这个比例称作转移比z。通过设置转移比z能够约束和调控失效节点负载在社团内和社团间的分配过程,这样更有利于研究级联失效作用对多社团网络鲁棒性的影响。



图3 节点失效后社团内负载重分配图Fig.3 Load redistribution diagram within and between communities after node failure
通过上述具体分配过程,总结出任意节点失效后负载重分配流程如下:


对集合ΓNid内所有节点的负载进行判断,若有节点负载大于临界负载,则该节点失效。
(4)对新的失效节点重复上述(1)~(3)中的分配过程,直到整个多社团网络再无失效节点为止。
2.3 节点失效判定标准
根据初始负载、容忍负载和临界负载的定义以及负载重分配策略,可以推导出任意一个节点在三个阶段内运行时失效的概率分布pt(i)为:

现有的大多数ML改进模型中,判定节点失效标准相对简单化,即当节点i实际负载小于其容量C(i)时,节点正常运行,反之节点失效。而本文添加了容忍负载和临界负载两个判断阈值,当节点i在容忍负载以下运行时,节点就不会失效。节点超过容忍负载运行时,自身负载越靠近临界负载,失效的概率就越高。当节点自身负载超过临界负载时,节点就立即失效。而节点负载处于这两个阈值之间时,相当于实际网络中节点可以过载运行一样。显然本文的设定更加贴合实际网络中节点在运行时可能出现的情况。
当网络在遭受攻击时节点被摧毁,网络内其他节点由于级联效应部分可能处于容忍负载状态或直接失效,失效的节点越少,网络的鲁棒性越好。本文定义失效节点数量与节点总数的比值称为失效比E,用失效比作为评估网络鲁棒性的标准。

其中,e表示失效节点的数量,N为节点总数量。
3 仿真分析
本文分别从节点负载模型参数和多社团网络结构两方面研究网络的级联失效问题。攻击策略为蓄意攻击初始负载最大的节点,随机攻击任意一个节点。为不失一般性,令a,b=1。
3.1 节点负载模型参数对级联失效作用的影响
设置网络生成参数为M=3,m=3,m0=3,p1=1/6,p2=1/3,p3=1/2,β=0.1,n=1,N=200,为避免偶然性,每次生成网络100个,每个网络仿真100次,仿真结果取平均值。
(1)介数调节参数θ
本文采用控制变量法,首先研究介数调节参数θ对级联失效作用的影响。设二次容忍负载参数p=0.5,转移比z=0.5,容忍负载参数λ=0.2,θ=[0.1,0.3,0.5,0.7],k=[0,2]。经过仿真,失效比E随临界负载参数k的变化趋势如图5和图6所示。
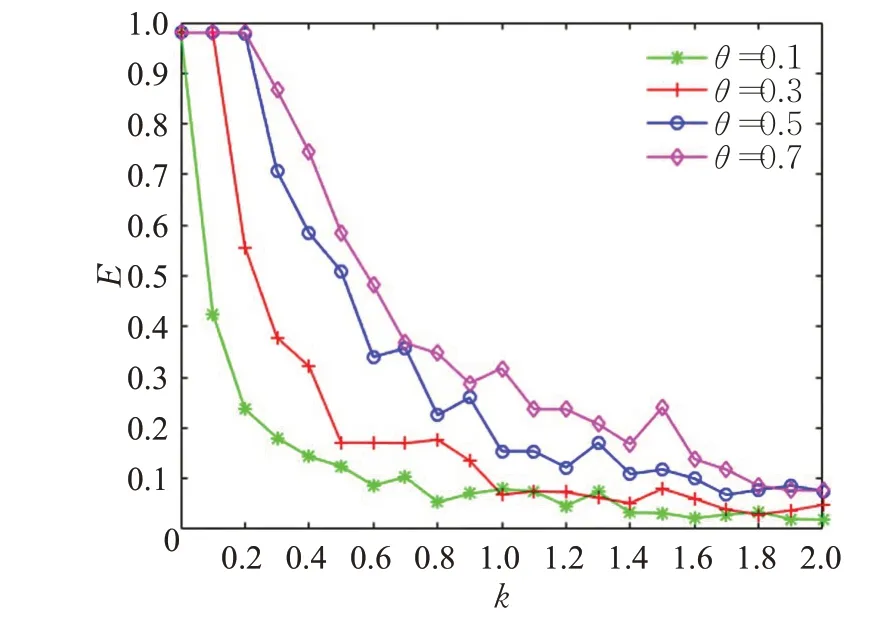
图5 蓄意攻击不同θ值时的E~k曲线Fig.5 Deliberately attacking E~k curve with differentθvalues
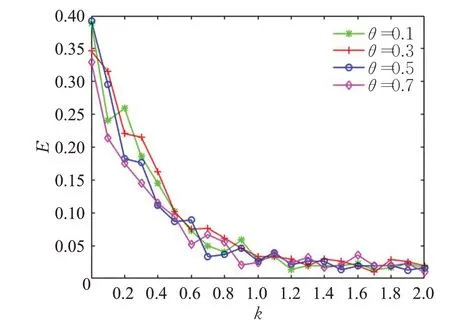
图6 随机攻击不同θ值时的E~k曲线Fig.6 Random attacking E~k curve with differentθvalues
从图5可以看出,失效比E随临界负载参数k的增加而减小。蓄意攻击时,在同一k值下θ值越小,失效比E越小,说明网络越具有鲁棒性,这是因为θ值越小,调整后的介数就越小,导致整个网络所有节点初始节点负载就越小,而且使节点初始负载相互之间的差值越接近,即初始负载分布越均匀,因此面对蓄意攻击更具有鲁棒性,这与文献[23]结论类似。另外,对于不同的θ值都有相应的临界阈值k1和k2(图4中,所有θ值的E~k曲线在k=2处均已平稳且趋向为0,故临界阈值k2必存在于k>2的某处)。当k<k1时E≈1,级联效应导致所有节点都失效。当k>k2时E≈0,一个失效节点无法引起级联失效,这同样与文献[23]的结论相似。
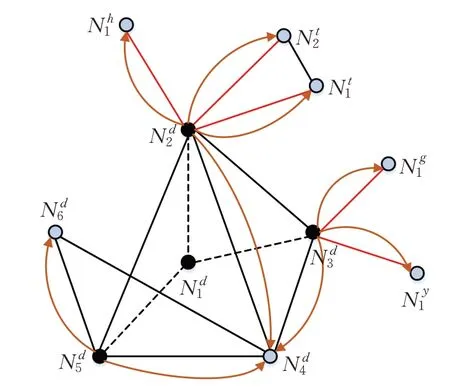
图4 节点失效后社团间负载重分配图(转移比z=0.5)Fig.4 Load redistribution diagram between communities after node failure(Transfer ratio z=0.5)
图6中,在随机攻击时,在参数k相同的情况下,不同θ值对应的失效比E几乎都相同,这是因为虽然θ值变化会引起节点初始负载的变化,但每一次随机选择到负载最大的节点概率只有0.5%。同时可以看出,在同一k值下,随机攻击比蓄意攻击失效比要小很多,说明网络在蓄意攻击时比在随意攻击时脆弱很多。
(2)二次容忍负载参数p
设置p=[0,0.25,0.5,0.75],k=[0,2],θ=0.5,z=0.5,λ=0.2。失效比E随临界负载参数k的变化趋势如图7和图8所示。

图7 蓄意攻击不同p值时的E~k曲线Fig.7 Deliberately attacking E~k curve with different p values

图8 随机蓄意攻击不同p值时的E~k曲线Fig.8 Random attacking E~k curve with different p values
从图7可以看出,蓄意攻击时,在0.1<k<1.5范围内,没有设置二次容忍负载的网络要比设置了二次负载的网络更加鲁棒,这是因为设置了二次负载的头节点的初始负载增大了许多,当这些头节点遭受攻击失效或者级联失效,过大的负载值分配给邻居节点,更容易引起邻居节点的失效,造成更加严重的级联失效问题。从图8可以看出,在随机攻击时,设置二次负载的网络在0<k<0.5的范围内要比未设置的网络的鲁棒性稍好一些,但幅度有限。因此得出为头节点设置二次容忍负载值的网络,面对攻击的总体鲁棒性要低于未设置的网络,这也从侧面说明了头节点在多社团网络中所处的位置很重要。
(3)转移比z
设置z=[0,0.25,0.5,0.75],k=[0,2],θ=0.5,p=0.5,λ=0.2。仿真结果如图9和图10所示。
图9中,蓄意攻击时没有设置转移比z的网络在k=[0,2]的范围内,失效节点数量都低于设置了转移比z的网络,说明后者鲁棒性要远高于前者,当z>0时,在k=[0,0.8]范围内,由于级联失效导致整个网络节点全部失效。这是因为节点失效时,初期将级联失效规模控制在本社团,而后将这些失效节点的负载向社团间转移,这些失效节点的级联失效作用会“引爆”整个网络。从图10看出,设置和未设置转移比的网络,在面对随机攻击时,失效比曲线在k=[0,2]范围内几乎相同,仅在k<0.2的初始范围内,设置转移比的网络能减少失效节点在整个网络引起的级联失效作用。因此,将级联失效控制在社团内部,不利于网络的鲁棒性。

图9 蓄意攻击不同z值时的E~k曲线Fig.9 Deliberately attacking E~k curve with different z values

图10 随机蓄意攻击不同z值时的E~k曲线Fig.10 Random attacking E~k curve with different z values
(4)容忍负载λ
设置λ=[0,0.1,0.2,0.3],k=[0,2],θ=0.5,p=0.5,z=0.5。仿真结果如图11和图12所示。

图11 蓄意攻击不同λ值时的E~k曲线Fig.11 Deliberately attacking E~k curve with differentλvalues
从图11和图12可以看出,蓄意攻击和随意攻击在参数λ=0和k=0时,即容忍负载和临界负载都等于0时,节点无法判断是否失效。同时在同一个k值下,λ值越大,网络就越鲁棒,λ值越小,网络就越脆弱。这是因为容忍负载升高,节点超容忍负载运行的概率就会相应降低,即节点肯定不会失效的概率升高。当节点i超过容忍负载运行时,根据公式(8)可以推导出此时失效的概率pt为:


图12 随机蓄意攻击不同λ值时的E~k曲线Fig.12 Random attacking E~k curve with differentλvalues
其中,W′(i)表示节点i实际负载,W(i)表示节点初始负载。从公式(10)可以看出,若初始负载W(i)和W′(i)固定,节点失效概率pt与λ和k呈负相关,即λ和k值越大,节点失效概率就越小,E值也就越小,这与图11和图12仿真结果相吻合。
从图12中可以看出,不同值曲线的区分度要比其他参数的曲线(图6、8、10)高很多,这是因为参数作为判断节点是否失效的一个标准,同等大小间隔的敏感度要比其他参数高很多,同时值变化也会引起处在容忍负载和临界负载之间的节点失效的概率,影响失效节点数同样比其他参数高很多。
3.2 多社团网络结构对级联失效作用的影响
从本文生成多社团网络的参数可以看出,影响网络结构的参数主要是m和β(本文默认n=1)。设置节点负载模型参数为θ=0.5,p=0.5,z=0.5,λ=0.2,k=[0,2],仿真结果同样取100次仿真平均值。
(1)社团内部连接数m
同样采用控制变量法,设置网络生成参数为M=3,m0=3,p1=1/6,p2=1/3,p3=1/2,β=0.1,n=1,N=200,m=[1,2,3],k=[0,2]。仿真结果如图13和图14所示。
从图13和图14可以看出,蓄意攻击和随机攻击时,社团内部节点连接数m越大,网络越脆弱。这是因为虽然社团内部节点连接数增加了,但度大的节点连接更多的新节点,会使初始负载变得更大,而负载小的节点几乎无变化,形成“马太效应”,使得社团内部结构无标度化,因此整个网络在面对攻击时越脆弱[1]。另外,当m=1时,随机攻击后网络节本无失效节点,这是因为此时网络的平均聚类系数为0.013 3,社团内节点之间连接程度非常低,网络无法引起级联失效反应。

图13 蓄意攻击不同m值时的E~k曲线Fig.13 Deliberately attacking E~k curve with different m values

图14 随机蓄意攻击不同m值时的E~k曲线Fig.14 Random attacking E~k curve with different m values
(2)社团间连接概率β
设置网络生成参数为M=3,m=2,m0=3,p1=1/6,p2=1/3,p3=1/2,n=1,N=200,β=[0.1,0.5,0.9],k=[0,2]。仿真结果如图15和图16所示。

图15 蓄意攻击不同β值时的E~k曲线Fig.15 Deliberately attacking E~k curve with differentβvalues
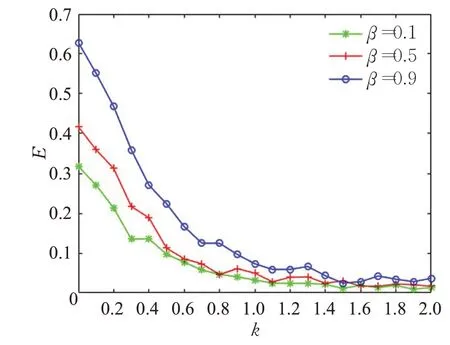
图16 随机蓄意攻击不同β值时的E~k曲线Fig.16 Random attacking E~k curve with differentβvalues
从图15和16可以看出,增加社团间连接概率,在蓄意攻击和随机攻击时,网络会越脆弱。β值越高,产生的社团间连接数越多,虽然会使社团间的耦合强度增大,但也会使网络中头节点的数目增加,经过仿真计算,β=0.1时,平均头节点个数为35个,β=0.5时为121个,β=0.9时为185个。头节点数量增加导致整个网络的平均路径长度变短,平均度增加,平均介数也相应增加,导致节点初始负载增大,在临界负载相对较小时,网络容易引发严重的级联失效反应,因此不利于网络的鲁棒性。
4 结束语
本文提出一种社团规模和社团结构可调的网络结构模型,以节点度和介数共同定义节点初始负载,根据社团结构特征,对头节点附加二次容忍负载,采用局部相邻节点分配策略处理失效节点负载,同时提出初始负载、容忍负载、临界负载三个阶段节点失效模型。通过对多社团网络级联失效问题进行了研究,得出结论为:(1)相同参数设置下,随机攻击时多社团网络鲁棒,蓄意攻击时多社团网络脆弱。(2)在蓄意攻击时,初始节点负载越高,网络越脆弱,越容易引起网络级联失效。(3)给头节点添加二次负载,蓄意攻击时会成为“爆发点”,引起严重的级联失效反应。(4)将失效节点负载分配控制在一个社团,越容易引发级联失效反应。(5)设置容忍负载和临界负载两阶段节点负载上限能有效提升网络鲁棒性。(6)社团内节点连接越均匀,网络越鲁棒。(7)社团间连接应选择初始负载较低的节点进行连接,以提高鲁棒性。

