注重回归课本 加强融会贯通
——2021年高考全国乙卷导数题的探究剖析与教学思考
余树宝, 肖婧钰
(1.合肥工业大学附属中学,安徽 合肥 230009;2.合肥师范学院数学与统计学院,安徽 合肥 230601)
函数是高中数学的重要知识点之一,导数为研究函数图像的切线、单调性、极值(最值)等方面提供了最有效的工具,因此在历届高考中,对导数及其应用的考查都非常突出.
在高考中,对导数及其应用的考查一般关注以下5个方面:利用导数的几何意义求函数图像的切线方程;利用导数求函数的单调区间,判断单调性;已知函数单调性求参数或其取值范围;利用导数求函数的最值(极值);利用导数解决函数的零点、方程的根或不等式的解等问题.重点考查理性思维和数学探索等学科素养,考查逻辑思维、运算求解等关键能力,渗透函数与方程、分类与整合、转化与化归、数形结合等思想方法.因此,高考导数题对学生素质和能力的要求较高.
针对这一重要考点,笔者以2021年全国数学高考乙卷第20题的教学为例,谈谈自己的教学过程、设计意图以及教学思考,供同行参考.
1 真题呈现
例1设函数f(x)=ln(a-x),已知x=0是函数y=xf(x)的极值点.
1)求a;

(2021年全国数学高考乙卷理科试题第20题)
2 试题分析
本题属于探索创新情境的综合性试题,具体考查函数极值点概念、导数在研究函数与不等式中的应用等必备知识.问题解决的过程中重点考查了逻辑思维和运算求解等关键能力,渗透了函数与方程、转化与化归、数形结合等思想方法.
从数学课程的核心素养上来看,本题考查了逻辑推理、数学运算、数学抽象、直观想象等核心素养.从高考考查的学科素养上来看,本题重点考查了理性思维和数学探索等学科素养.
第1)小题是一道基础题,由极值点定义,不难得到关于a的方程,求解可得a的值;第2)小题是本题的难点,最佳路径是先用分析法,将复杂不等式g(x)<1转化为较简单不等式x+(1-x)ln(1-x)>0,然后通过构造函数φ(x)=x+(1-x)ln(1-x),将问题转化为求函数的最值或值域.此类问题在历年的高考中经常出现,如2020年和2021年的浙江省数学高考解答题都考查了不等式的证明问题,值得重视.
3 教学过程
3.1 函数的极值点
本课以问题为导向,通过师生互动、合作交流等形式开展教学活动.
问题1什么是函数极值点?
学生思考后回答.教师设疑引导学生深入理解极值点及相关概念.
追问1函数极值点是“点”吗?满足f′(x0)=0的x0一定是f(x)的极值点吗?极值点与极值的关系是什么?
设计意图旨在让学生回顾此概念,进一步加深对此概念的全面理解,从而完成第1)小题.
问题2本题的第1)小题如何解决?请有逻辑地书写解答过程.
学生在理解了极值点的概念之后,由已知“x=0是函数y=xf(x)的极值点”,可得“x=0是方程y′=0的根”,从而解得a的值.
此题虽是一道简单题,但若概念不清,或对复合函数求导有误,则可能就是一道易错题.因此求导公式与法则,特别是复合函数的求导法则,要求学生务必准确记忆,熟练应用.
另外,从严谨性来说,需要验证当a=1时,x=0是函数y=xf(x)的极值点,因为“f′(x0)=0”是“x0是f(x)的极值点”的必要条件.
学生的解答过程中有可能没有验证,这就是为什么教师让学生独立思考,自主运算,给出问题的解答思路,并认真且严谨地书写解答过程的原因.
教师给学生一定的时间,让学生独立完成解题过程,并展示解题步骤.
第1步(复合函数求导):设h(x)=xf(x),则
第2步(代入求值):因为x=0是函数y=xf(x)的极值点,所以h′(0)=0,即lna=0,故a=1.
第3步(验证有效性):当a=1时,
从而当x<0时,h′(x)>0;当0 综上所述,a=1. 设计意图通过让学生独立地写出完整的解题过程,培养学生规范准确且有逻辑地表达数学语言和书写解题过程的能力. 这是一道变式题,问题3与例1都属于极值点问题,且均含有参数,只不过例1条件中直接告知极值点,而此题中没告诉,因此两题的解答思路并不完全相同. 师:f(x)有两个极值点意味着f′(x)=0有两个不相等的实根.这显然是根据方程根的个数求a的取值范围,如何解答? 生1:首先肯定是求导数f′(x),f′(x)=ex-ax. 师(追问):根据刚才的分析,接下来是不是直接分析方程f′(x)=0的根? 教师给予肯定,通过参变量分离,利用函数与方程思想、转化思想和数形结合思想来解决问题. 图1 然后讨论增减性:当x<0或0 师:此时,我们要根据什么来判断实数a的取值范围呢? 设计意图师生合作,集思广益,共同完成了这道变式题,旨在加深学生对函数极值点概念的理解,积累极值问题可以通过参变量分离法转化为不含参数的函数问题来解决,同时体会函数与方程思想、数形结合思想在问题解决过程中的价值. 问题4回忆一下,不等式常用的证明方法有哪几种? 学生思考后回答.不等式常用的证明方法有比较法、综合法、分析法、数形结合法等. 设计意图旨在回顾相关知识,构建完整的知识体系,引导学生选择适当的方法完成第2)小题的证明. 问题5例1第2)小题g(x)<1的证明思路是什么? 生5:可用分析法进行证明.要证明g(x)<1,即证 只需证x+ln(1-x) 师:分式中的分母xln(1-x)是正数吗? 生6:不是.由不等式 得x<0或0 只需证 x+ln(1-x)>xln(1-x), 即证x+(1-x)ln(1-x)>0对任意x<0或0 师(追问):接下来如何解决? 生7:构造函数φ(x)=x+(1-x)ln(1-x),把问题转化为证明φ(x)>0恒成立即可. 师:把不等式证明问题转化为函数的最值问题,即用函数来研究不等式是一种有效的方法.前面的转化有意义吗?为什么不直接证明g(x)max<1? 教师让学生分别证明φ(x)min>0和g(x)max<1,经历两个不同函数的最值求解过程,体会它们的优劣. 对φ(x)求导得φ′(x)=-ln(1-x).当x<0时,φ′(x)<0;当0 对于g(x),求导得 设计意图这是一个不等式的证明问题,也是导数应用中常见的问题.问题解决的关键往往是“转化”,即“不等式”向“函数”转化.将不等式证明的问题,即不等式恒成立问题转化为函数的最值问题,利用导数知道函数单调性之后,用单调性法求函数的最值.整个过程渗透了数学中的四大思想,即函数与方程思想、分类讨论思想、转化思想和数形结合思想. 另外,历年的高考题一般都能在课本中找到源头.追根溯源,例1的源头是人教A版《数学(选修2-2)》习题1.3B组第1题: 例2证明:不等式lnx 例2拓展到例1的推理路径是:由lnx 即 亦即 1-x+xlnx>0, 于是1-(1-x)+(1-x)ln(1-x)>0(其中x<1且x≠0), 进而 x+(1-x)ln(1-x)>0, 即 x+ln(1-x)>xln(1-x), 亦即 故 g(x)<1. 问题是数学的心脏,但高考复习不能成为单纯的解题教学,不能让“课堂讲题,课后做题”成为常态,不能忽视对基础知识,特别是数学概念的回顾与理解,否则就会造成学生对概念的发现、发生与发展模糊不清或理解不深的问题.本题中的“函数的极值点”这一概念,容易错误地认为是图像上较低点或较高点或是拐点,也容易错误地认为它是“导函数值为0的根”的充要条件. 本题由h′(0)=0得到a=1后,在不失严谨性的条件下,一定要验证当a=1时,是不是保证了条件“x=0是函数y=xf(x)的极值点”. 我们常说“抓纲务本”,其实这里的“本”就是“教材”或“课本”.高考命题者主要依据考纲(或课程标准)和教材进行命题,多数高考题都能在“课本”中找到源头,因此在备考复习时,千万别忽视了课本.回归课本,特别要加强对课本例习题的研究与剖析,注重对课本例习题进行变式训练,因为课本中的例题和习题是专家学者们在编写教材时精心筛选来的,深具典型性、代表性,十分有研究价值.挖掘教材,变式训练,能培养学生举一反三的能力,也符合我们“熟能生巧”的教育古训.文献[1]提出:把握数学核心概念的本质,明晰什么是数学的通性通法.因此,摒弃“题海战术”及“重复训练”,回归教材,以变式练习来帮助学生掌握解题技能,积累解题经验. 当前乃至今后的高考,更加强调考查的基础性、综合性、应用性和创新性,特别是综合性,要求对同一层面的知识、能力、素养能够横向融会贯通,形成完整的知识结构网络[2].如对于方程、不等式、数列等问题,我们要引导学生学会用函数的观点来理解并加以解决.譬如方程根的问题就是函数的零点问题,也是函数的图像与x轴的交点问题;不等式解的问题就是函数图像的问题,也是函数的值域问题.当然数学中的转化思想在此起着关键作用. 高三教学不是孤立地就单一知识点或问题的教学,而应成为相关知识或问题联系的教学.现在新课程倡导的大单元教学法其实也说明了这一观点的重要性.


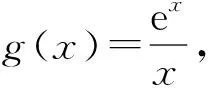

3.2 不等式与函数的关系
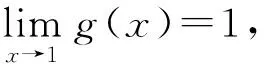
4 教学建议
4.1 注重概念教学
4.2 注重变式训练
4.3 注重融会贯通

