浅谈数字“1”在最值问题中的应用
曹江谊
(义乌市第五中学,浙江 义乌 322000)
“1”是数字发展的开始,也是人类最早用于记数的单位,更是在数学解题中不寻常且又奇妙的存在,在诸多知识板块的问题求解中都能见到它活跃的身影,尤其在最值问题中.无论是不等式的最值问题,还是与函数、解析几何、线性规划等其他知识相结合的问题,灵活运用数字“1”进行式子转化,常能快速找到解题思路,从而使问题迎刃而解.
本文从平时的教学中总结了多类最值问题,试图通过数字“1”在这些题目中的巧妙应用,让学生深刻体会数字“1”在最值问题中的重要作用,尝试引导学生发掘数字“1”的各种巧思妙用,以此提高他们的观察运算能力和逻辑思维能力.
1 在不等式最值问题中的应用
在不等式最值问题中,如何巧妙地使用数字“1”是解题的关键.它的恰当、灵活运用,不仅能达到化繁为简、化难为易的效果,而且还能让学生在解题中感受到“柳暗花明又一村”的惊喜.求解时,数字“1”有相乘、配凑、分离、消减等多种应用技巧和方式.下面就“1”的应用技巧简单举例介绍.

( )
A.m≥4或m≤-2 B.m≥2或m≤-4
C.-2 解若x+2y>m2-2m恒成立,则 m2-2m<(x+2y)min. 当且仅当x=4,y=2时取到等号,所以 (x+2y)min=8, 即 m2-2m<8, 解得-2 ( ) A.3 B.4 C.10 D.16 进行适当变形,得到 利用基本不等式即可求得最小值为4. 解由已知x+y=1,可得 x+1+y+2=4, 当且仅当x=0,y=1时取到等号.故选B. 这里对数字“1”应用了直接相乘和配凑相乘的解题技巧,特别是在凑系数时,我们要根据题意将目标式进行拆分,从而找到缺少的系数.通过技巧为基本不等式的使用创设条件,成功地将式子变形为能相乘为常数的结构,从而达到快速解题的目的. 在有关分式的题目中最常用的方法是分离常数法.本题就是抓住题目中分式的结构特征,分离出数字“1”,并对式子进行巧妙的变形,使其出现两数之积为定值的结构,以此利用基本不等式进行求解.分离技巧往往应用于分式最值问题中,此时还需注意分子、分母在配凑时的系数变化情况. 例4已知正实数x,y满足x2+xy=1,则y2-2xy的最小值是______. 解由x2+xy=1,可得 此题应用的是数字“1”的消去技巧.除了上述方法外,数字“1”的应用技巧还有很多,如代入法、加减法等.学生在解题过程中,容易形成思维定势,我们除了要掌握典型题型中“1”的妙用外,在平时的解题中,更要学会灵活多变,不拘泥于套路,具体问题具体分析. 解三角形是三角函数中的重要组成部分.在求解三角形的过程中,往往需要结合正余弦定理对原等式进行“边化角”或“角化边”运算.在“角化边”的运算中通常可以得到几条边之间的等式关系,巧妙地对等式中的“1”进行转换,往往会得到意想不到的好处. 图1 ( ) 因为C∈(0,180°),sinC≠0,所以 即 又因为A∈(0,180°),所以A=120°. 如图1,由S△ABC=S△ABD+S△ACD,知 得 bc=b+c, 即 当且仅当b=c=2时取到等号.故选C. 图2 2a+3b=12. 评注本题综合了线性规划的知识.在解题时,首先需要根据线性规划知识建立关系式,然后利用得到的关系式巧用“1”进行代换,将所求式子巧妙变形为两数之积为常数的形式,进而求得最值. f′(1)=0, 从而 2a+b=3, 于是 评注函数知识是高中数学中的重要内容,常常与其他知识综合进行考查,与不等式相结合的最值问题就是常考的内容.因此在解题时,要抓住问题的本质,结合函数的概念、性质、图像变换等得到“两数之和或两数之积为定值”的结构,最终利用数字“1”的各种应用技巧快速解题. 解析几何中的最值问题往往综合性较强,常与距离、角度有关.在解题时,需要根据题意挖掘出关于“1”的等式,从而达到化繁为简的效果. ( ) 图3 解如图3,椭圆的焦点在y轴上,且当点P为椭圆的左、右顶点时,∠APB取得最大值120°,则 又 得 |PM|+|PN|=2a=6, 当且仅当|PM|=2,|PN|=4时取到等号.故选D. 图4 分析本题考查立体几何的空间位置关系,首先要找到线面之间的联系,然后运用求体积的相关知识将空间问题转化为不等式关系,最后结合“1”的妙用求解. 解如图4,设点A在底面BCD的射影为E,则△BCD的外接圆半径为 从而 所以 由等体积法可得 VA-BCD=VO-ABC+VO-ACD+VO-ABD+VO-BCD 即 又因为x,y都是正数,所以 以上是笔者积累和总结的“1”在不等式及与其他知识相结合最值中的应用.在具体问题中,我们要针对不同类型的目标式采用相应的有关“1”的方法进行求解,特别是与其他知识相结合的题目中,要善于挖掘题中隐含的“1”的条件.只要能够灵活运用有关“1”的各种方法,举“1”反三,时刻牢记基本不等式的运用条件“一正、二定、三相等”,最终往往能化繁为简,化难为易,起到“1”点通的妙效[1]. 拓展学生的探索创新思维,提高其逻辑解题能力,进而培养他们的数学核心素养,这一直是数学教学的核心要求和终极目标.笔者通过数字“1”在最值问题中的灵活妙用,试图从中找到线索,以期在培养学生数学综合能力方面达到抛砖引玉之效.






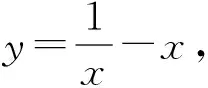


2 在与其他知识相结合的最值问题中的应用
2.1 与三角函数相结合




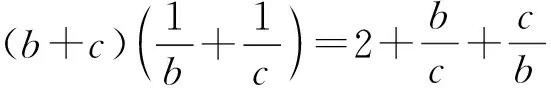
2.2 与线性规划知识相结合





2.3 与函数相结合



2.4 与解析几何相结合

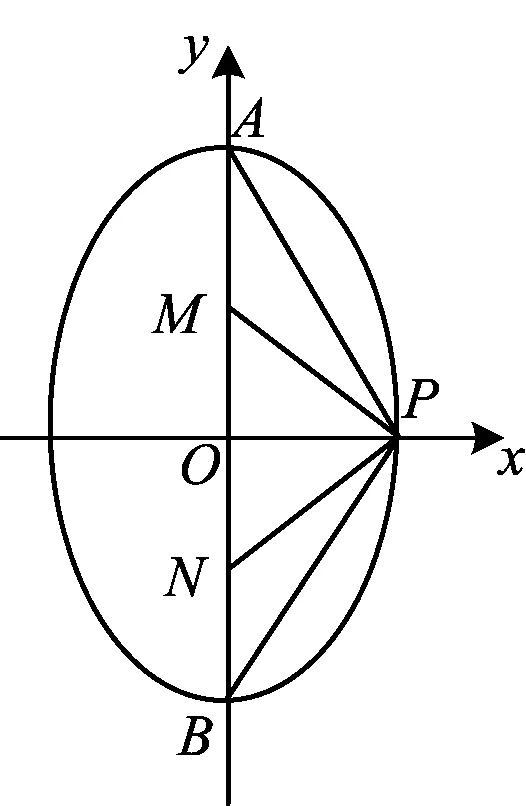


2.5 与立体几何相结合





