关于数形结合思想在小学数学教学中的应用策略

吴云红

摘要：在小学数学教学中，数形结合思想的运用，能够帮助学生更好的学习数学知识，提升学生课堂学习效果。文章以数形结合思想在小学数学教学中应用为研究对象，对数形结合应用原则进行阐述，对如何利用数形结合思想进行教育工作，提出几点建议，希望对相关人士提供参考。

关键词：数形结合思想;小学;数学教学;策略

引言：数形结合思想的运用，将抽象难懂的数学知识简单化，使学生在教师的指导下可以快速掌握基础知识，并运用在实际中。如何将数形结合思想运用在课堂教学活动中呢？本文就此进行分析。

1数形结合思想在数学教学中应用原则

1.1等价性原则

在数学课堂教学活动中，若想发挥数形结合思想教育功能与价值，应遵循等价性原则，保证数量与图形之间转化的合理性，为学生展示更加丰富的数学知识，培养学生数学思维，提升课堂教学效果。所谓的等价性，就是数学图形的几何意义与数的代数意义能够相互转化，让学生在图形与数量的转化过程中理解课本知识，构建数学知识结构。运用数形转化思想进行教学时，应以学生实际学习情况为基础，结合学生数学基础、学习能力选择适合的方式進行课本知识教学，利用这一思想方法提升学生基础知识学习效果，提高教学质量。

1.2双向性原则

小学数学课堂教学活动中，需要坚持双向性原则，保证代数与图形之间能够互相转换，为学生理解数形结合思想打下坚实的基础[1]。若是出现数的代数意义只能转化为图形的几何意义，而图形的几何意义无法转化为数的代数意义，不仅无法展示数形结合思想的优势，同时也会影响学生理解数学知识。因此，应坚持双向性原则，结合教学内容，合理运用数形结合思想，以此保证教育工作实施效果。

2小学数学课堂教学中数形结合思想应用策略

2.1数学概念中应用，夯实学习基础

在小学数学课堂教学活动中，概念是教学的重点，也难点。部分小学生因为不理解数学概念，而无法实现进一步学习[2]。课堂教学活动中，将数形结合思想运用在概念教学中，利用不同的数学图形，辅助学生理解数学概念，利用基础知识解决问题，提升自身数学学习能力。利用数形结合思想进行概念教学时，应尊重学生的主体地位，结合学生实际学习情况，设计数形结合教学活动，使学生在教师的引导与帮助下更好的参与课本知识学习，以此提升课堂教学效果，为后续深入学习打下坚实的基础。

例如，进行《长方形和正方形》内容教学时，为了让学生对正方形、长方形的特点形成深刻的记忆，掌握基础知识，渗透数形结合思想，利用数学图形讲解正正方形、长方形的概念，使学生快速了解这两个平面图形的特点。在教学活动开始前，教师可以将生活中常见的正方形、长方形以多媒体视频的方式呈现出来，如冰箱、电视等等，并对学生问道：同学们，你们熟悉视频中的图片吗？这些物体的形状有什么特点吗？提问后，让学生认真观察视频图片，并说出自己观察到的内容。这时教师可以将长方形、正方形画出来，并结合视频图片，讲解概念内容，让学生一边观看图形，一边思考教师讲解的内容，正确认识长方形与正方形。通过数形结合思想的运用，提升概念教学效率，使学生在有限的时间内快速理解课本知识，保证基础知识学习有效性。

2.2引导学生画图，提升数学学习效果

数学课堂教学活动中，教师可以引导学生根据学习内容画出相应的数学图案，让学生在自主实践的过程中掌握数形结合思想，为后续更好的学习打下坚实的基础。对于学生来讲，日常学习中不仅要掌握数学知识、解题方法，同时还要不断的实践，掌握数学思想，为初高中数学知识学习做好铺垫。因此，在课堂教学活动中，需要教师为学生提供实践学习的机会，引导自主画图解决问题，以此提升学生的画图能力与数形结合思想应用能力。需要注意的是，学生学习基础不同，学习能力与效果也不同。引导学生采用数形结合思想学习时，教师应做好教学引导工作，对学生进行适当的点拨，让学生在教师的引导下探索更深的数学知识，在实践中掌握学习方法与技巧。

2.3解题中应用，培养学生的数学思维

数学教育工作开展的最终目标，就是培养学生知识应用能力，使学生掌握运用数学知识解决实际问题的能力。在课堂教学活动中，将数形结合思想运用在数学问题中，引导学生运用所学在知识解决问题，学会数学思想方法的灵活运用[3]。利用数形结合思想进行问题教学时，教师可以将解题的思路与方法渗透教学中，使学生在潜移默化中掌握解决问题的方法，养成好的学习习惯，以此提升课本知识教学效果，提高学生解决问题能力。

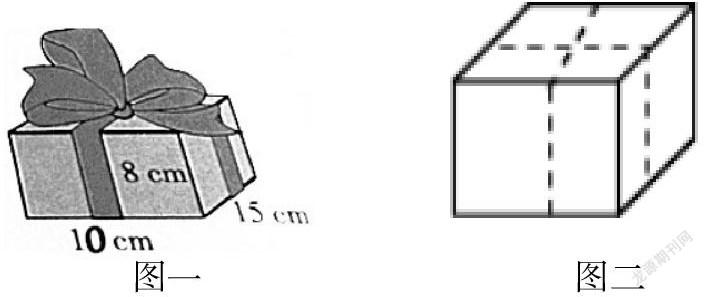
例如，如图一，一个长方体礼盒的长、宽、高分别是15cm、10cm、8cm.

（1）要在这个礼盒所有的棱上都粘上一圈胶带，至少需要多长的胶带？

（2）要用一根绳子捆扎这个礼盒，如果绳子的接头处长20cm，那么至少需要多少厘米长的绳子？

解决这一问题时，可以让学生将根据问题，结合图片信息，画出一个长方体，如图二，然后利用图形解决问题。经过学生的思考与讨论后，得到：（1）根据长方体的棱的特征，12条棱中互相平行的一组4条棱的长度相等，它的棱长总和=（长+宽+高）×4;由此解答。即：（15+10+8）×4=33×4=132（厘米）（2）根据长方体的特征：12条棱分为互相平行的3组，每组4条棱的长度相等，由图形可知：需要彩带的长度等于2条长+4条高+2条宽+打结用的20厘米即可.即：15×2+10×2+8×4+20=30+20+32+20=102（厘米）

结语：

总而言之，在小学数学教学中，数形结合思想的运用，提升学生概念学习效果，培养学生多方法解决数学问题能力。课堂教学中，将此运用在不同教学环节，培养学生的数学思想，提升课本知识教学效果，促使学生全面发展。

参考文献：

[1]顾丽凤.运用数学思想，提升学生思维能力——数形结合思想例谈[J].科学咨询（教育科研），2021，（04）：241-242.

[2]曹玉珍.小学数学教材中数形结合思想的比较研究——以人教版、北师大版和苏教版“图形与几何”内容为例[J].教育导刊，2020，（07）：68-72.

[3]黄冰冰.从直观认识走向深入理解——高阶思维视域中儿童数形结合思想的培养[J].教育观察，2020，（24）：132-133.

课题编号：JCJYC210412019

课题名称：数形结合思想在小学数学教学中的实践研究

2660500520271