一种新的类范德蒙矩阵

张华民，郭竹梅，盛家乐， 殷红彩

(1.安徽科技学院 信息与网络工程学院，安徽 蚌埠 233030；2. 安徽财经大学 管理科学与工程学院，安徽 蚌埠 233030)

0 引言

范德蒙矩阵和它的逆矩阵在多项式插值、无线通信和信号处理等领域有重要的应用[1～3]。鉴于范德蒙矩阵的重要应用, 基于范德蒙矩阵又衍生出了许多与范德蒙矩阵关系密切的矩阵, 如广义范德蒙矩阵[4,5]、合流范德蒙矩阵[6,7]和类范德蒙矩阵[8]等。

同上面的工作类似，本文通过利用初等对称多项式构造一种类范德蒙矩阵，计算表明这种类范德蒙矩阵和范德蒙矩阵的行列式相等，同时这种类范德蒙矩阵的逆矩阵也和范德蒙矩阵关系密切。为了表述方便引入下面的记号。

设集合K={k1,k2,…,kr},从集合k中任选r-1个数可构成次数从1到r-1的初等对称多项式。用记号σs(i)表示从k中去掉ks(s=1,2,…,r), 从余下的r-1个数中分别选取i(i=1,2,…,r-1)个数构成的多项式。例如从中选取k2,…,kr,则可构成如下的多项式：

…，

σ1(r-1)=k2k3…kr.

这样的σs(i),s=1,2,…,r,i=1,2,…,r-1，共有r×(r-1)个, 它们依次是

σ1(1),…,σr(1);σ1(2),…,σr(2);σ1(r-1),…,σr(r-1).

借助这样的初等对称多项式构造矩阵Ar(k1,k2,…,kr)和Br(k1,k2,…,kr)分别记为

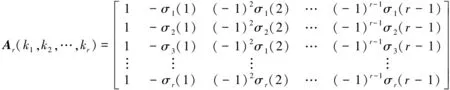
(1)

(2)

称矩阵Ar(k1,k2,…,kr)为类范德蒙矩阵。

1 主要结论

记集合K中的元素生成的r阶范德蒙矩阵Vr(k1,…,kr)为

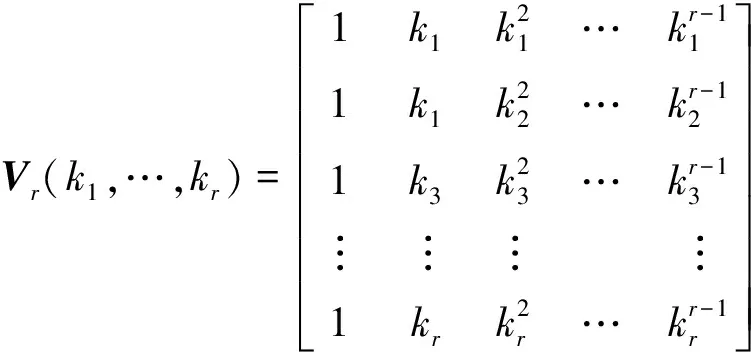
(3)

则矩阵Vr(k1,…,kr)的行列式detVr(k1,…,kr)的值为

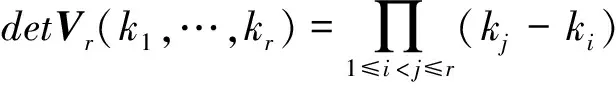
(4)

记矩阵Wr(k1,…,kr)为

(5)

引入交换矩阵P,

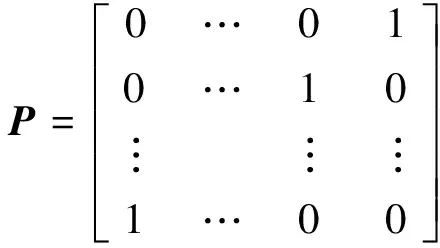
则有

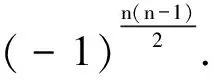
(7)

本文的主要结论是类范德蒙矩阵Ar(k1,k2,…,kr)与Vr(k1,k2,…,kr)行列式的值相同, 即有

定理1 沿用(1)(3)两式中的记号, 则矩阵Ar(k1,k2,…,kr)和Vr(k1,k2,…,kr)有相同的行列式, 即有

(8)

类范德蒙矩阵Ar(k1,k2,…,kr)的逆矩阵和矩阵Wr(k1,k2,…,kr)有密切的联系, 具体如下。

定理2 根据(1),(5)式中矩阵Ar(k1,k2,…,kr)和Wr(k1,k2,…,kr)的含义, 则有

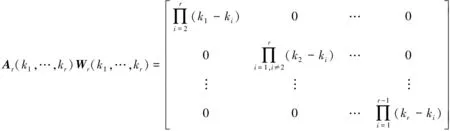
(9)

2 定理1的证明

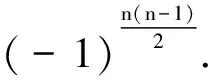
定理3 沿用(2)式中矩阵Br(k1,k2,…,kr)的记号, 则有

(10)

证明 下面对矩阵Br(k1,k2,…,kr)的阶数r用数学归纳法来证明。为了表述方便, 接下来的证明中用集合K中元素的初等对称多项式来代替σs(i),s=1,2,…,r,i=1,2,…,r-1.

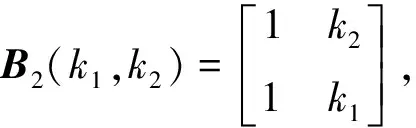
下面假设对r-1阶的矩阵Br-1(k2,…,kr)结论是成立的, 则对r阶矩阵Br(k1,…,kr)取行列式可得

=(k1-k2)…(k1-kr)detBr-1(k2,k3…,kr)

=(k1-k2)…(k1-kr)…(kr-1-kr)

根据数学归纳法原理, 定理3中的结论是成立的。 证毕。

根据矩阵A2(k1,…,kr)与B2(k1,…,kr)的关系, 可知定理1是成立的。

3 定理2的证明

下面通过证明一个关于初等对称多项式的恒等式来证明定理2.

证明 先证明下面恒等式成立

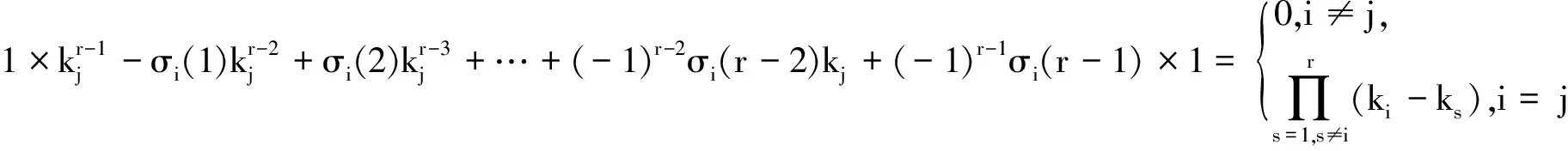
(11)

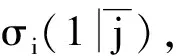
σi(1)=(k1+…+ki-1+ki+1+…+kj-1+kj+1+…+kr)+kj

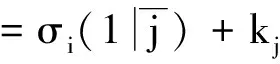
(12)

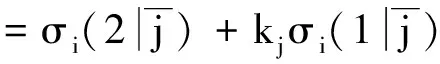
(13)

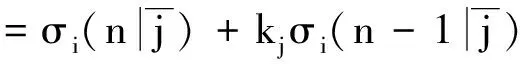
(14)

分别当n=1,2,…,r-1时将恒等式(14) 代入(11)式左端可得

=0

(15)

当i=j时, (11) 式可化成

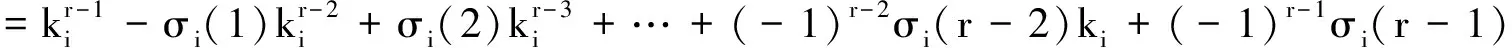
(16)

而我们可以直接验证下式是成立的

=(ki-k1)(ki-k2)…(ki-ki-1)(ki-ki+1)…(ki-kr)

(17)

到此我们证明了

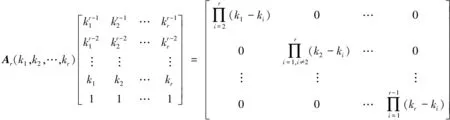
(18)

至此, 定理2得以证明。 证毕。

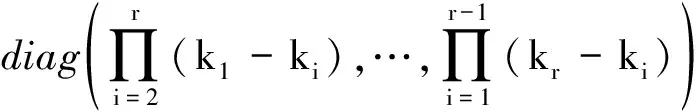
4 总结

以初等对称多项式为元素, 本文提出了一种类范德蒙矩阵。它的行列式和范德蒙矩阵相等或仅相差一个符号。 通过利用初等对称多项式的恒等式得到了类范德蒙矩阵和范德蒙矩阵逆的关系。 利用这种关系可以求得范德蒙矩阵的逆矩阵。