不等式的指数推广与应用
费清平,叶秀婷
(1.深圳市南头中学;2. 惠州学院数学与统计学院)
0 引言
不等式问题是数学竞赛中的热点问题,每一届数学竞赛中几乎都会涉及到不等式[1]。因此,研究不等式、对不等式进行推广,不仅有利于不等式本身的发展,而且一定程度上促进了数学竞赛的发展。
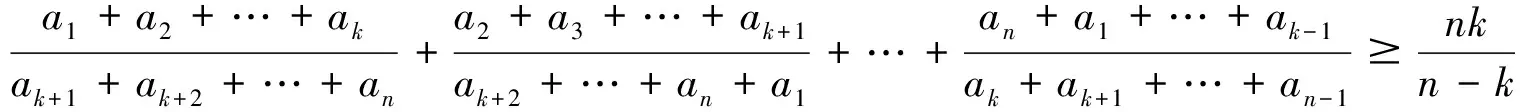
(1)
其中a1,a2,…,an∈(0,+∞),n>k≥1(k∈+)。当k=1时,不等式(1)变成:
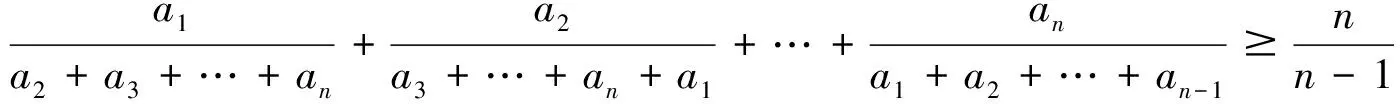
(2)
其在形式结构上与一类关于不等式的数学竞赛题目具有很大的相似性,例如文献[3]中的特例1,特例2,特例5,特例6等等。归结起来,这类题目结构如下:

(3)
是由n个正数构成的n个分式和不等式,其中n个分母都是n-1个正数之和,且每个正数在分母中共出现n-1次,分子都是不包含在分母中的正数的m次幂[4]。
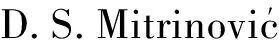
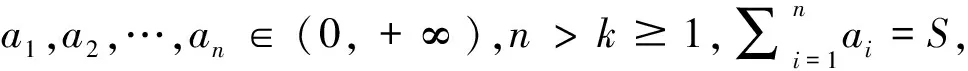

(4)
证明 记bi=ai+ai+1+…+ai+k-1,(an+1=a1,an+2=a2),即
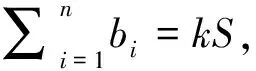
不妨设b1≥b2≥…≥bn>0,则b1α≥b2α≥…≥bnα>0,且0 (S-b1)-β≥(S-b2)-β≥…≥(S-bn)-β. 运用切比雪夫不等式得 又运用幂平均不等式,由于α≥1,所以有 因此, 又因为-β<1,所以有 于是 从而 即有 因此不等式(4)得证。 特别地,在不等式(4)中,取k=1时可得以下推论, 推论1 设a1,a2,…,an∈(0,+∞),n>1,n∈, 且α≥β>0,α≥1,则 (5) (6) 证明 因为α≥β≥1,对正数x1,x2,…,xn运用幂平均不等式 则 对不等式(6)左边各分式的式子运用以上不等式,然后再利用不等式(4)得不等式(6)的左边 再次运用幂平均不等式,因为β≥1,所以有 则 从而有 所以,不等式(6)得证。 (注:定理1与定理2中要求指数α≥1,但当α≤-1时,有-α≥1,此时仍然满足两个定理的条件,因此当指数α≤-1时两个定理仍适用。) 下面简要给出本文结果在形如不等式(3)这类数学竞赛题中的便捷应用,例如引言部分提到的几个例子。 例1 (第2届“友谊杯”国际数学竞赛)若a,b,c是正数,证明: 证明 在不等式(5)中,取n=3,α=2,β=1得 故原不等式得证。 注:在不等式(6)中,取k=1,n=3,α=2,β=1同样可得上述证明结果。 例2 (第31届IMO预选题)若a,b,c,d是满足ab+bc+cd+ad=1的非负实数,试证: 证明:在不等式(5)中,取n=4,α=3,β=1得 因为ab+bc+cd+ad=(a+c)(b+d)=1,所以 [(a+c)+(b+d) ]2≥4(a+c)(b+d) ⟹(a+b+c+d)2≥4 因此, 原不等式得证。 注 在不等式(6)中,取k=1,n=4,α=3,β=1同样可得上述证明结果。 例3 (第28届IMO预选题)若a,b,c是三角形的三边边长,且2S=a+b+c.试证: 这里m≥1. 证明 在不等式(5)中,取n=3,α=m,β=1得 注 在不等式(6)中,取k=1,n=3,α=m,β=1同样可得以上证明结果。 例4 (第四届数学冬令营)设x1,x2,…,xn都是正数(n≥2),且 求证: 运用幂平均不等式得 所以 故原不等式得证。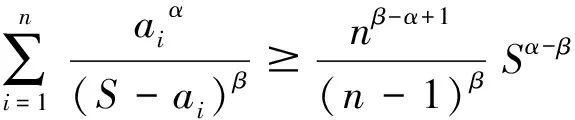
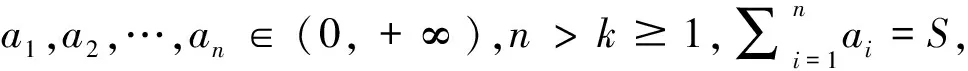

2 新不等式在一类数学竞赛题中的应用

