基于APOS理论的初中数学概念教学实践初探
徐明敏


[摘 要] APOS理论是一种关于数学概念教学的建构主义理论. 通过对APOS理论的理解和研究,笔者基于APOS理论设计了一次“直线和圆的位置关系”的概念教学实践,分析和探讨了初中学生在APOS理论四个阶段体现的对数学概念的理解情况,期待APOS理论在数学概念教学实践中能有效地提升教学效率.
[关键词] APOS理论;教学模式;数学概念;理解情况
前言
APOS理论是在20世纪80年代末至90年代初由美国数学家杜宾塞斯(Dubinsky)等人在数学教育研究实践中发展起来的一种数学教学理论. APOS理论是一种关于数学概念教学的建构主义理论,该理论强调教学过程中应将数学概念与现实社会中的实例相结合,学生通过自身的经验,将两者联系起来,让学生经历数学概念的形成过程. APOS理论将数学概念形成过程分为以下循序渐进的四个阶段:操作或活动阶段(Action)、过程阶段(Process)、对象阶段(Object)、模型阶段(Schema). 其中,“操作或活动阶段”指学生通过一系列外显的数学探究活动去获得概念的内隐本质的过程;“过程阶段”是“操作或活动阶段”的内化和提升,即学生通过对外显的数学探究活动的进一步思考,抽象出概念的本质特征,将新概念纳入自己的认知结构;“对象阶段”是给抽象出的概念的本质特征赋予形式化的定义和符号,使其成为一个具体的对象;“模型阶段”是学生知识积累的发挥阶段,将新概念与其他概念建立联系,形成知识的综合模型,将这个模型纳入自身的认知结构,与已有知识建立新的实质性联系. 在这四个阶段完成过程中,学生的认知结构在不断地进行调整,使自己不断加深对数学概念的理解,学生的认知水平也会由此上升到更高层次.
通过对APOS理论的理解和研究,笔者基于APOS理论设计了一次“直线和圆的位置关系”的概念教学实践,分析和探讨了初中学生在APOS理论四个阶段体现的对数学概念的理解情况,让笔者深有感触,由此以本文章展现出来,期望对初中数学教师设计概念教学模式有所帮助.
基于APOS理论的初中数学概
念教学模式的实践过程
1. 操作或活动阶段
“操作或活动阶段”是学生通过一系列外显的数学探究活动去获得概念的内隐本质的过程,虽说“外显的数学探究活动”是该阶段学生获得概念的内隐本质的关键所在,但是其中的“外显”容易让人误会“探究活动”只是具体实体的动手表象活动,使得不少教师对课程使用的工具和时间的安排容易产生困惑和烦恼,这在一定程度上会让教师本身对课程失去兴趣和控制. 其实,“外显的数学探究活动”还包括一些“抽象的经验或知识”对学习对象内隐本质的显现.
环节1 温故知新.
回顾1:点和圆的位置关系有_____种. 如图1所示,如果⊙O的半径为r:①点P在圆_____,OP_____r;②点P在圆______,OP______r;③点P在圆______,OP______r.
回顾2:如图2所示,已知AB=4 cm:①以A为圆心,5 cm为半径画圆,点B在圆_____;②以A为圆心,4 cm为半径画圆,点B在圆____;③以A为圆心,3 cm为半径画圆,点B在圆____.
设计说明 对“点和圆的位置关系”的温故知新,是对上位概念的回味,由回味对知识进行迁移,点和圆的三种位置关系对后面类比教学“直线和圆的位置关系”埋下了伏笔. 在回顾1和回顾2中,让学生明白除了用“形”之外,还可以用“数”来判断位置关系,这不仅渗透了转化与化归思想,而且让学生深刻体会了数形结合思想的应用.
2. 过程阶段
“过程阶段”是“操作或活动阶段”的内化和提升,在课程中让学生明白仅以“形”来判断位置关系是模糊的,应加以数量关系进行判断更具严谨性和科学性,将这样新的研究意识纳入学生的认知系统中. 不仅如此,在过程中通过观察、实验、讨论、合作等数学活动的开展,可使学生更加熟悉探究和创造,逐步了解探索、解决问题的一般方法——类比、转化等.
环节2 类比、转化.
探究1:如果把“点”换成“直线”,直线和圆的位置关系有哪些?你能够借此在纸上画出来吗?(学生绘画后可以利用动画演示图片)
探究2:你画的图有公共点吗?有几个?
探究3:如果⊙O的半径为r,圆心到直线的距离为d,类比两者的大小:①直线和圆相交?圳d____r,直线与圆有____个公共点;②直线和圆相切?圳d____r,直线与圆有____个公共点;③直线和圆相离?圳d____r,直线与圆有____个公共点.
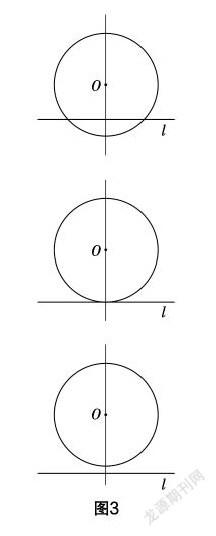
探究4:判断下列直线和圆的位置关系(如图3所示).
设计说明 由于学生对“点和圆的位置关系”的理解和掌握,知识的正迁移可以让学生以点在圆内、圆上、圆外类比到直线和圆的三种位置关系——相交、相切、相离,并与相应的公共点的个数相接连;但是当直线和圆相交太近时,學生无法从“形”的角度对直线和圆相交的公共点的个数进行判断(如图3所示),让学生开始明白除去用“形”之外,更加严谨和科学的是用“数”来判断直线和圆的位置关系,这对后面用数量关系来判断位置关系做下了铺垫.
3. 对象阶段
“对象阶段”是给抽象出的概念的本质特征赋予形式化的定义和符号,使其成为一个具体的对象. 在“直线和圆的位置关系”的教学中,“对象阶段”主要进行的就是,学生在了解了直线和圆的三种位置关系的定义后,从数量关系的角度去研究直线和圆的三种位置关系. 在这个阶段,学生会将动态的直线和圆的位置关系转变成静态的、整体的结构关系——圆的半径r(或直径)与圆心到直线的距离d的数量关系?圳直线和圆的公共点的个数?圳直线和圆的位置关系.
环节3 用数量关系判断位置关系.
问题1:如果现在已知图3中圆的直径是15 mm,圆心到直线的距离分别是7.49 mm,7.50 mm,7.51 mm,那么图3中直线和圆分别是什么位置关系?它们各有几个公共点?
问题2:已知圆的半径为4,设圆心到直线的距离为d,如果直线和圆相交,那么d的取值范围是_______;如果直线和圆相切,那么d的取值范围是________;如果直线和圆相离,那么d的取值范围是______.
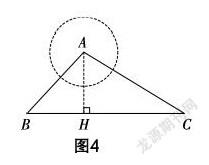
问题3:如图4所示,点A是一个半径为300 m的圆形森林公园的中心,在森林公园附近有B,C两个村庄,现要在B,C两村庄之间修一条长为1000 m的筆直公路将两村连通.经测量,得∠ABC=45°,∠ACB=30°,问:此公路是否会穿过该森林公园?请经过计算说明.
设计说明 利用圆心和直线的数量关系(距离和半径)来判断直线和圆的位置关系,是学生学习直线和圆的位置关系的性质与判定的阶梯,加强了学生“数”“形”相互转化的意识和应用,让学生理解判断直线和圆的位置关系为什么要转化成圆心到直线的距离和圆的半径的大小关系来实现.
4. 模型阶段
“模型阶段”是学生知识积累的发挥阶段,将新概念与其他概念建立联系,形成知识的综合模型. 可以说,模型阶段是学生知识总结和拓展阶段,通过持续联系、加工和深化,会使学生对新学的数学概念的理解不断加深,学生的思维和认知水平也会上升到更高水平和更高层次.
环节4 总结和拓展.
总结:使用数据来判断直线和圆的三种位置关系:
拓展1:直线l与⊙O相切于点A,直径AB与直线l有怎样的位置关系?
拓展2:圆心到直线的距离如何计算?有哪些方法?
拓展3:直线和圆的公共点的个数与二次函数有什么联系?
设计说明 通过填表的方式引导学生进行总结,回顾本节课所学的主要知识,帮助学生养成总结的好习惯;拓展的内容比较适合学生课后自主探索,通过探索让学生体会知识之间的联系,更容易加深和完善学生对认知结构的建立,这对后期的学习打下了基础.
思考
从APOS理论可以看出,数学概念教学模式的实践是循序渐进的概念建构过程,在整个过程中,每个阶段都缺一不可. 相应的教学活动在整个过程中或许有些不同,但每个阶段都自有成立的关键之处. 在“操作或活动阶段”,外显的数学探究活动需是学生能够亲身感知、有兴趣去思考的教学活动,在活动中能体验出概念的内隐本质,这是活动设计的关键. 在“过程阶段”,要让学生从直观转化到抽象,再从抽象转化到对象,这既是过程阶段的教学步骤,也是教学指向. 在“对象阶段”,是师生忙碌一阵后看到结果显示的重要时间,无论结果是大或者小,是多或者少,对每位学生来说,都应该熟悉和体验到自己的收获. 在“模型阶段”,知识的综合模型并不是此段学习内容的终点,它是某个层次和更高层次的枢纽,这样的意识是师生都应该具有的.
APOS理论是一种教学理论,更加适合数学概念教学,期望有更多教师能够了解它、研究它,得出更多的使用它的策略.
3644501908223

