多极矩分析的教与学探讨
余 天,姚 欣,林 方,齐建起,张志友,聂 娅,王 磊,朱建华,龚 敏
(四川大学 物理学院,四川 成都 610065)
多极矩分析是一种重要的方法和计算策略[1]。由静态电磁场多极矩展开而引入的电多极子和磁多极子作为基础的电磁物理模型,不仅在电磁场理论中常被用于从物质微观电磁构型出发阐明宏观电磁效应,还在刻画物质微观结构及其相互作用等方面也发挥着重要作用。例如,原子核一般都具有特征旋转对称轴而不是电荷均匀分布的理想点电荷这一核物理发现在历史上就是基于电多极矩解析原子超精细谱而得到的[2].此外,多极矩分析和多极子模型在行星物理和地磁学等交叉学科领域也起着关键作用[3-5].
在本科物理及相关专业培养中,多极矩分析通常只在电动力学课程中有所涉及[6-8].多极矩展开表示、多极子模型以及多极子与静态电磁场的相互作用是多极矩分析的三个主要内容.本文结合我们的教学实践,就上述三方面内容展开梳理讨论.在多极矩展开表示讨论中除补充了国内教材中较少涉及的场点包围在源区内部情景下的内部多极矩展开外,还着重分析了静电多极矩展开笛卡儿表象(Cartesian Representation)和球谐多极矩展开表象(Spherical Harmonics Representation)的关系;在多极子模型理解上我们强调了多极子是蕴含着源构形信息的理想点源模型而不是电荷或电流分布的真实空间构型;在受力与力矩两方面给出了多极子与外电磁场相互作用精确到四极子的计算结果.
1 两种物理情景下的多极矩展开式
多极矩展开可以有两种物理情景:场点位于有限源区外部的外部多极矩展开(Exterior Expansion)和场点包围在源区内部的内部多极矩展开(Interior Expansion)[9].外部多极矩展开适用的情形是:源分布在有限空间中且其线度R远远小于待求场点到源(中心)的距离,此时取原点在源分布中心附近,如图1(a)所示,则远源场点的电磁势函数可以展为关于场点距离的收敛函数.若场域被包围在有限源分布空间的内部,但仍满足场源间距远大于场域空间线度R,则取坐标原点在场域中心附近,如图1(b)所示,原点附近场点的电磁势函数也可以展为关于场点距离的收敛函数,此即为内部多极矩展开情形.

图1 (a)外部多极矩展开和(b)内部多极矩展开情形示意图,其中深色区域代表源分布区域.
多数教材侧重于外部多极矩展开介绍[6-8],特别是在直角坐标系下将有限源区外部远源场点的静电标势和/或静磁矢势表为关于场点距离幂的逐项递减级数形式.这样的安排方便借由我们熟悉的直角坐标系直观的介绍多极子模型.但是只介绍直角坐标系表示的外部多极矩展开显然是不全面的.多极矩展开的应用并不是仅仅限于处理场点在源区外部的情形.大量科研和实际应用中样品都是置于电极或电流线圈等源所限定的空间内部.例如,高能加速器中用于束流外部的四极子磁体实现带电粒子的强聚焦[10],利用外部电极实现束流加速[11],这些都属内部多极矩展开的情形.
在教学中如何用数学语言统一而自然地引入多极矩展开的两种情景?以下分别由三维泰勒展开和二项式定理出发进行的分析.
1.1 由三维泰勒定理讨论多极矩展开的两种情景
直角坐标系下的多极矩展开,就是要将远源场点处的静态电磁势函数——静电标势φ和静磁矢势A——展为关于场点距离幂的逐项递减级数.
一种便宜的方法是从熟悉的单变量函数在其可微领域附近的泰勒级数出发,将以矢量为自变量的可微标量函数f(ξ)展开为逐项递减的级数,即有三维泰勒展开[9]:
f(ξ+)=f(ξx+x,ξy+y,ξz+z)=[exp(
f(ξ+)=[exp(
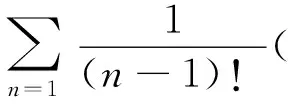
(1)
现在取矢量为自变量的标量函数:
(2)
显然地对任意ξ≠0其都是可微的,由此可得到展开式:
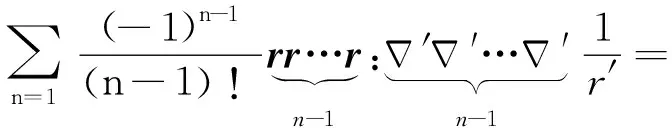
(3)
这里我们用“:”代表并矢的多重点积,具体点积运算重数由运算符前后的张量阶数明确.上式表明远源场点处的静电标势φ和静磁矢势A展为关于场点距离幂的逐项递减级数有两种情况:
1) 当r>>r′时,应有
φ(r)=
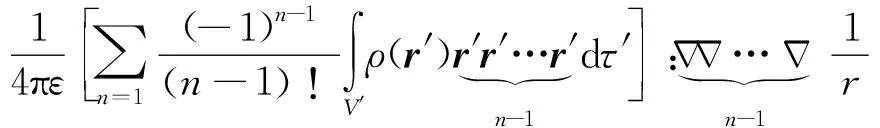
A(r)=
(4)
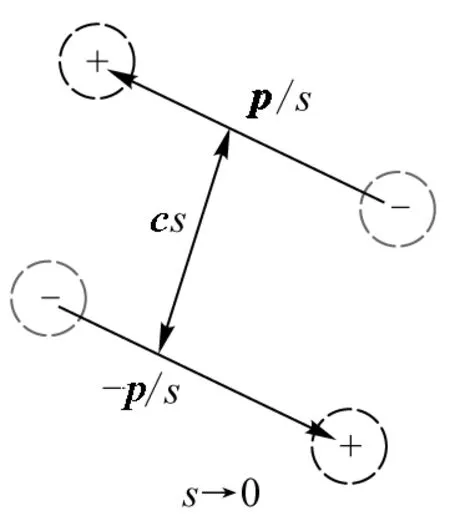
2) 当r< φ(r)= A(r)= (5) 其中ρ为源电荷密度,J为源电流密度.上述括号形式已经把关于源点的积分同关于场点的运算分开,这还表明源区V′与场域V无重合. 前述(4)式和(5)式表述的静电标势和静磁矢势只涉及矢量-张量的抽象运算,无关任何具体坐标系选择,故可以视作静电标势和静磁矢势外部和内部多极矩展开的一般表示.认识到这一点有助于后续厘清球谐多极矩展开与上述多极矩展开的联系与区别.展开式(4)和(5)中第n项关于源点的积分系数就是相应的2(n-1)极矩,特别地习惯上称n=1时积分系数为单极矩,n=2时积分系数为偶极矩. 基于三维泰勒展开的方法,其优点是可简明方便的直接引入张量表示的多极矩展开一般形式,自然而然地获得外部和内部两种多极矩展开情景的一般表达式.但初学电动力学和电磁场理论时,通常面对的一个教学困难是学生对高阶张量及其微分规则并不熟悉,理解和掌握三维泰勒展开的张量形式较为困难.为此,不妨从学生相对熟悉的二项式定理出发建立多极矩展开一般形式[3,16]. 二项式定理指出对任意有理指数α和|x|<1,恒有级数表示式: (6) 若定义场点距离和源点距离中较大和较小者分别为: (7) 则不难得到: 将上式按r>的幂次整理得到: (8) 利用上式我们来展开库仑积分表示的静电标势,容易有: 1) 若r>>r′,即有r>=r;r<=r′,则 (9) 只需由不太复杂的并矢运算关系[12]就可将式(9)前几项改写为张量及其微分形式: 这正是由三维泰勒展开得到的张量表述的外部电多极矩展开的前几项. 2) 若r< (10) 利用简单的并矢运算类似地可得张量形式: 这正是由三维泰勒展开得到的张量表述的内部电多极矩展开的前几项. 不难发现式(9)和式(10)也无涉具体坐标系的选择,故由二项展式出发也可得到电多极矩展开一般形式.磁矢势显然可以类似展开,不再赘述. 在多极矩展开的表示理论中,经典教学参考书常给出电磁势函数在球坐标系下一种同时按场点距离幂和球谐函数阶展开为级数的表示[2,9].具体而言,采用式(7)定义的符号,由勒让德函数母函数定理我们有: (11) (12) 以静电标势的多极矩展开为例,上式表明我们恒有: (13) 基于此可以方便地由静电标势的库仑积分式得到: φ(r)= (r>>r′) φ(r)= (r< 这便是静电标势的球谐多极矩展开,其展开式第l项中反映源分布特性的积分系数称为l阶静电球谐多极矩. 容易验证球谐多极矩展开与前面多极矩展开具有类似的性质.值得指出的是静电球谐多极矩展开还提示了球坐标系下拉普拉斯方程通解的基础解系的物理含义:静电标势拉普拉斯方程在球坐标系下分离变量通解为 (15) 静磁问题通常比照静电问题处理,但教学参考资料中鲜有静磁球谐多极矩展开的具体介绍.这主要是由于历史上磁场球谐多极矩分析最早是基于磁标势-磁荷观点由高斯(Carl Friedrich Gauss)在分析地磁场时系统提出的[7],磁矢势的“前生”——电动力学势——还要等6年后的1845年才由纽曼(Franz Ernst Neumann)在尝试建立法拉第电磁感应定律的定量关系时提出[13].磁荷-磁标势观点下的静磁球谐分析的成功,使得高斯引入的磁标势球谐多极矩被广泛接受,故惯用静磁矢势球谐多极矩展开保持了高斯引入的磁标势球谐多极矩并不能直接由(13)式结合源电流密度在球坐标系下分解直接得到.详尽讨论静磁矢势球谐多极矩展开超出本文范围,这里仅给出静磁标势和静磁矢势外部球谐多极展开的结果[17,18]: (16) (17) 其中大括号表示的系数反映源分布特性即为静磁外部球谐多极矩。 在多极矩分析应用实践中,鉴于球谐函数的性质是广为熟知的,因此将静态电磁场同时按场点距离幂和球谐函数阶展为级数较仅按场点距离幂展开运用更加广泛和便利.多极矩分析的两种展开表示方式教与学中,学生经常遭遇的一个困惑是上述多极矩展开的两种表示相互关系如何?特别是教学中静电多极矩分析常由直角坐标系下三维泰勒展开切入讲解,不少学生容易误认为“静电球谐多极矩展开就是静电多极矩展开在球坐标系中的表示”,这显然是欠妥当的.首先,场源间距的倒数的展开的张量运算表示(3)式和矢量运算表示式(8)式均不涉及具体的坐标系选择,即使在球坐标系下具体写出也不涉及球谐函数,这容易由(8)式直接看出.其次,比较两种多极矩展开表示中第m项多极矩涉及的元素个数还可以发现,若按场点距离幂展开,反映源特性的多极矩可有m2个元素;若同时按场点距离幂和球谐函数阶展开,由球谐函数性质可知其至多只有(2m-1)个独立元素.当m≠1时两者元素个数不等,显然多极矩分析的两种表示的关系不是坐标系选择的不同.事实上,静电场的多极矩展开本质是将远源场点处的静电标势按转动群的不可约表示进行分解,两者差异在于独立基矢选择不同.具体而言,第m项球谐多极矩在转动下按l=(m-1)秩球坐标能量变换,而按场点距离的幂展开得到的第m项多极矩按n,n-2,n-4,…,nmin秩球坐标能量变换,这里的n=(m-1),当n为偶数时nmin=0,当n为奇数时nmin=1.可见静电多极矩展开的两种表示是多极矩展开的不同表象:一般称按场点距离幂展开为多极矩展开的笛卡尔表象,称按场点距离幂和球谐函数阶同时展开为球谐多极矩表象[6,9].应当说明的是,静磁场矢势按场点距离幂和球谐函数展开时,磁多极矩沿用了基于磁荷-磁标势的标量磁多极矩,故磁矢势的两种表示不符合一般意义下表象变换关系. 理解各项多极矩的含义并由此抽象出物理模型——多极子——是多极矩分析的另一主要内容.受教材和教学中电多极矩直观图示影响常容易忽略多极子的理想点源特性. 容易验证,一对等量异号电荷构成的“物理电偶极子”的电偶极矩满足笛卡尔表像下多极矩展开定义的电偶极矩.然而 “物理电偶极子”的电标势还存在着其它高阶项,并不与电多极矩展开引入的电偶极矩的对应电标势一致.因此,“物理电偶极子”不是多极矩展开得到的电偶极子所要刻画的电荷分布.正确理解电偶极项所描述的电荷分布,必需借助极限思想,事实上,只有当电偶极子 (18) 在s→0极限下退化为位于原点的点源时,其激励的静电场具有与静电多极矩展开偶极矩项相同的电标势[9,14,15]. (19) 图2 这一结论还可以结合静电标势基本方程,由电偶极子的等效电荷分布得到: (20) 关于原点的δ函数形式表明电偶极子是理想点源模型. (21) 图3 多极矩展开引入电四极子的一种构型示意图 按照上述方法可以递次求出高阶电极矩刻画的电荷分布物理模型:电2n极子是由等大异号一对电2n-1极矩子构成的位于原点的点电荷分布模型.值得指出的是,教学中虽然电四极矩等高阶项贡献也可以由位于原点的四个点电荷分析得到,但是由2n极子通过错位和极限构建2n+1极子能更好的体现各阶多极子间的关系,也更加符合多极矩展开所蕴含的物理思想[15].类似的分析也适用于笛卡尔表象下静磁外部多极矩物理意义的分析[16],此处不再赘述. 如何理解多极子是位于原点的点源但蕴含着源构形信息?这可以回归到多极矩展开本身去思考.多极矩展开将远源场点处电磁势函数展为位于原点的一系列等效点源的电磁势函数叠加(注意到多极矩展开式总是关于场点距离幂的级数即可看出这一点).同时,这些等效源激励的电磁势函数又与特定电荷分布或电流分布在远源处激励的电磁势一致,在这个意义下我们说这些位于原点的点源还蕴含着电荷分布或电流分布的空间构型信息.例如,前面已经提到过“物理电偶极子”在远处场点激励的静电场与电偶极子激励的偶极电场对应相同的电标势;恒定环形电流在远处场点激励的静磁场与磁偶极子激励的偶极磁场对应相同的磁矢势.换言之,多极矩作为点源也蕴含着源分布的信息,是指其所激励的电磁场与特定空间构形源分布在远源处场点激励的电磁场对应着相同的电磁势函数,而不是要在几何意义下的点源内部去寻找特定分布信息. 电多极子在外电场中的能量、受力和受力矩已有不少文献论述,包括由静电互能出发基于变分法获得受力与受力矩作用[7,8],或者从多极子等效电荷分布出发求出受力和受力矩[17].这里再介绍一种通过将外电场展开求多极子受外电场力和力矩的推导. 若激励外电场E′的源到给定电荷体系ρ的距离与该电荷分布的线度R相较足够大,或者说待讨论电荷分布区域处的外电场变化足够平缓,则取坐标原点在待分析电荷分布附近,可将外电场E′在原点附近类似静电标势做多极矩展开: (22) 注意到在电荷分布ρ的原点附近区域将E′展开时,E′展开的场点就是ρ的源点,我们直接得到: (23) 换言之,由电荷分布ρ确定的电单极子、电偶极子以及电四极子在外电场中受到的电场力为: FQ=QE′, (24) 注意上述各式对任意外电场均成立,不限于静电场. 利用上述外电场E′的展开式也可直接求出给定电荷分布在外电场中关于原点所受力矩精确到电四极矩项的结果: (25) Tp=p×E′, (26) 同样地,上述结果对任意外电场均适用,不限于静电场的情况. 类似推导也可以给出电流分布J所确定的磁多极子在外磁场B′变化足够平缓时所受力和关于原点的力矩.精确到磁四极矩其所受到外场作用力的第k分量可以写为: (27) 上式已经利用到恒定电流分布激励的静磁场无磁单极矩.利用恒定电流分布确定的得磁偶极矩m和磁四极矩M,我们也即有: (28) 特别地,当外磁场为静磁场时(28)式可以写为矢量形式: (29) 而磁四极子相关项改写为矢量-张量形式也即, 在此基础上可进一步求磁多极子在外磁场中关于原点的力矩为 (30) 表为矢量张量形式即有: (31) 可见磁偶极子和磁四极子在外静磁场中受到的力矩分别为 Tm=m×B′, (32) 多极矩分析因较集中地涉及张量运算、特殊函数以及物理模型的极限抽象构建,在数理要求整体已较高的电动力学课程教学中也算突出难点.但目前国内关于多极矩分析教与学的文献仍相对较少.本文围绕多极矩展开表示、多极子模型以及多极子与静态电磁场的相互作用力和力矩展开探讨,希望有助于梳理多极矩分析教与学的主要内容,厘清基本概念与重要模型,拓展和丰富多极矩分析相关知识,对电动力学课程多极矩分析的教与学有所助益.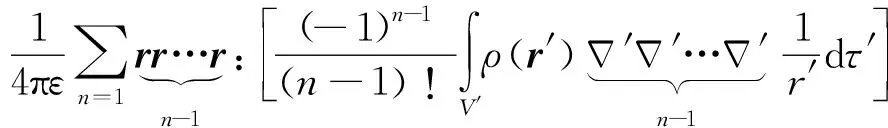

1.2 由二项式定理得出两种情景下的多极矩展开式


2 多极矩展开的另一种表示——球谐表象
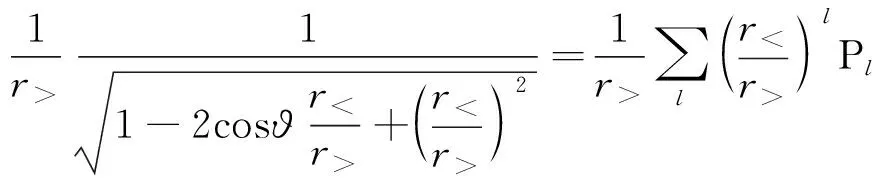


3 多极子是点源模型


4 多极子与外场的相互作用力和力矩
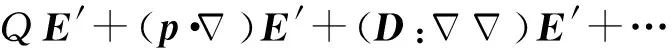
5 总结

