双凹球面相控聚焦超声波场的产生与可视化
孔令昊,李嘉琪,曾天佑,曾育锋,2
(1. 华南师范大学 物理与电信工程学院,广东 广州 510006;2. 华南师范大学 物理国家级实验教学示范中心,广东 广州 510006)
超声相控阵技术在声悬浮中有重要的应用价值,2018年邓双[1]实现了二维平面内的声场移动控制及多微构件的自动化声操作,2019年李文斌[2]运用相控聚焦原理实现了单凹球壳装置内的声场构建及颗粒稳定悬浮,2019年王英伟[3]提出了凹球面阵列聚焦的计算方法并实现了双凹球面装置内声场及颗粒的轴线运动. 2013年Takayuki Hoshi等人[4]利用相对的平面阵列,通过相控阵聚焦技术进行三维声学操纵. 2020年Spyros Polychronopoulos[5]等人利用了相对的平面阵列实现了空间中多个颗粒悬浮. 然而,众多实现声场三维移动的声悬装置均采用平面阵列,而凹球面的驻波声场特性均优于平面[3],目前对于双凹球面阵列的研究又局限于轴线移动. 故本实验吸收两者优点,首创在双凹球面阵列上通过相控聚焦算法实现声场三维移动,并使用COMSOL Multiphysics多物理场仿真软件进行声场的数值模拟.
为了进一步检验相控聚焦理论在声场三维移动应用中的正确性,使用纹影法观测声场. 纹影法最早被实验物理学家罗伯特⋅胡克使用一个透镜和滤光器(观察者眼睛虹膜)来观察蜡烛烟雾中的热气流. 随后,人们对纹影系统中的光路、滤光器、观察设备、透镜等参数进行了不断改进,逐渐发展成Z型、直线型和反射式等不同特点的纹影系统,根据研究需要被应用于各种领域,其中在流体特性观察与测量以及晶体结晶时周围浓度的观测等领域被广泛应用[6,7].
DirkMöller等人[8]在2013年提出了纹影可视化在研究超声粒子操纵装置方面存在巨大潜力,胡斌等人[9]在2018年利用纹影系统观察声光介质内部的超声波图像,并测量了超声波在晶体内的传播速度,纹影法在超声波场中一般用来进行声场测量、声场特性观察以及声场校准等. 由于纹影法得到的声场图是三维声压强度的积分,在声场呈现的精度方面会有限制,但与一般的流体测量系统相比,因为它利用的是光学原理,可以实现快速成像,且不会对已存在的声场造成创伤,与此同时,其配合相机还可实现声场的瞬态成像或动态影像拍摄,故纹影法是复杂声场分析的一个简便有效的工具.
1 装置设计及相控聚焦驻波悬浮理论
1.1 凹球面双发射极声悬浮装置
该装置由双凹球壳支架(如图1所示),以及用于超声发射的72个超声换能器(上下各36个)组成.
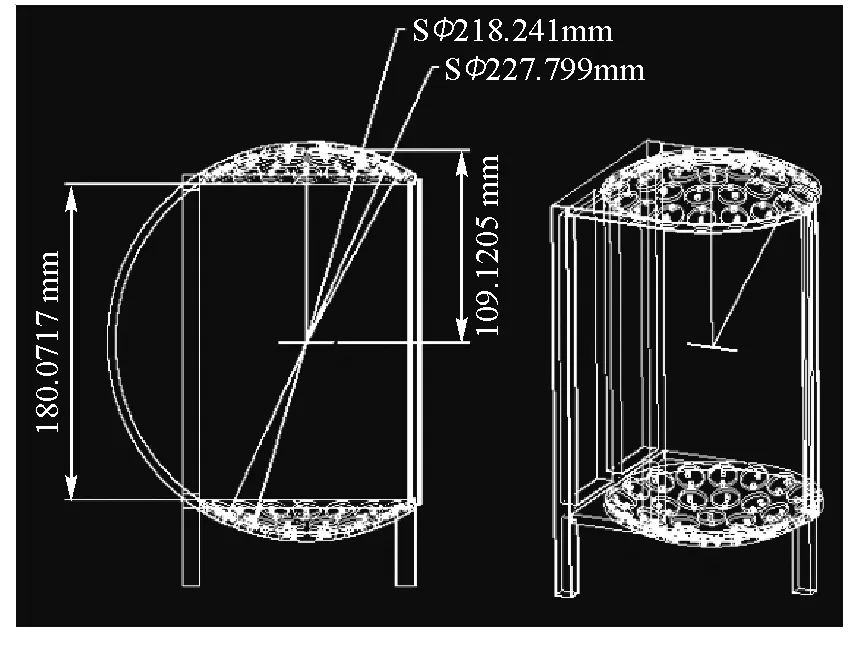
图1 双凹球壳支架
双凹球壳支架上下两球面为同一球体的一部分(非半圆),为了使声场可三维移动的范围更广,本文设计的球体半径为109.12 mm,球壳内径为218.24 mm,球壳外径为227.79 mm,上下球壳边缘相距180.07 mm.上下球壳分别设计了36个圆形凹槽(包括引脚孔),用以放置超声换能器,超声换能器型号为TCT40-16T,外径为16.0 mm.球壳分为三层,从球壳顶点往下,以每层6、12、18个换能器槽孔依次递增. 中间与底部都设计了支撑柱,用以保持支架的稳定.
1.2 相控聚焦原理
相控聚焦的基本原理为:通过控制每个阵元声源信号与基准声源信号的相对时延t,进而控制每个阵元声源信号的初相位,使得阵列中各阵元声源发出的超声波的传播在聚焦点区域处于同一相位,实现声压的叠加,声波在聚焦点附近形成类似驻波的声场. 相对时延t的计算方法如下.
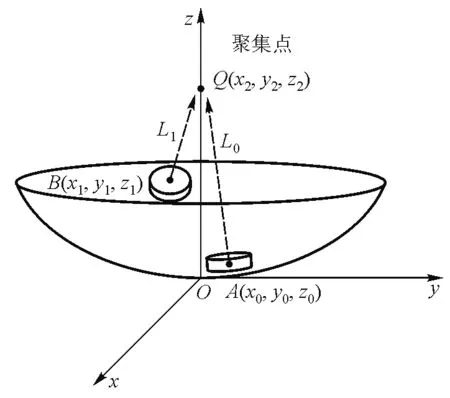
图2 相控聚焦原理图
如图2所示,选取凹球壳上某一个超声波换能器A的信号作为基准信号,该超声波换能器的几何中心的坐标为A(x0,y0,z0),其到聚焦点Q(x2,y2,z2)的距离为L0,凹球壳上某一超声波换能器B的几何中心的坐标为B(x1,y1,z1),其到聚焦点Q(x2,y2,z2)的距离为L1,有
(1)
(2)
当装置所处空间的声速为v时,超声波换能器B的信号要相对于A的信号提前或延迟时间t,t<0则B的信号要相对A的信号延迟,t>0则B的信号要相对A的信号提前,其中
(3)
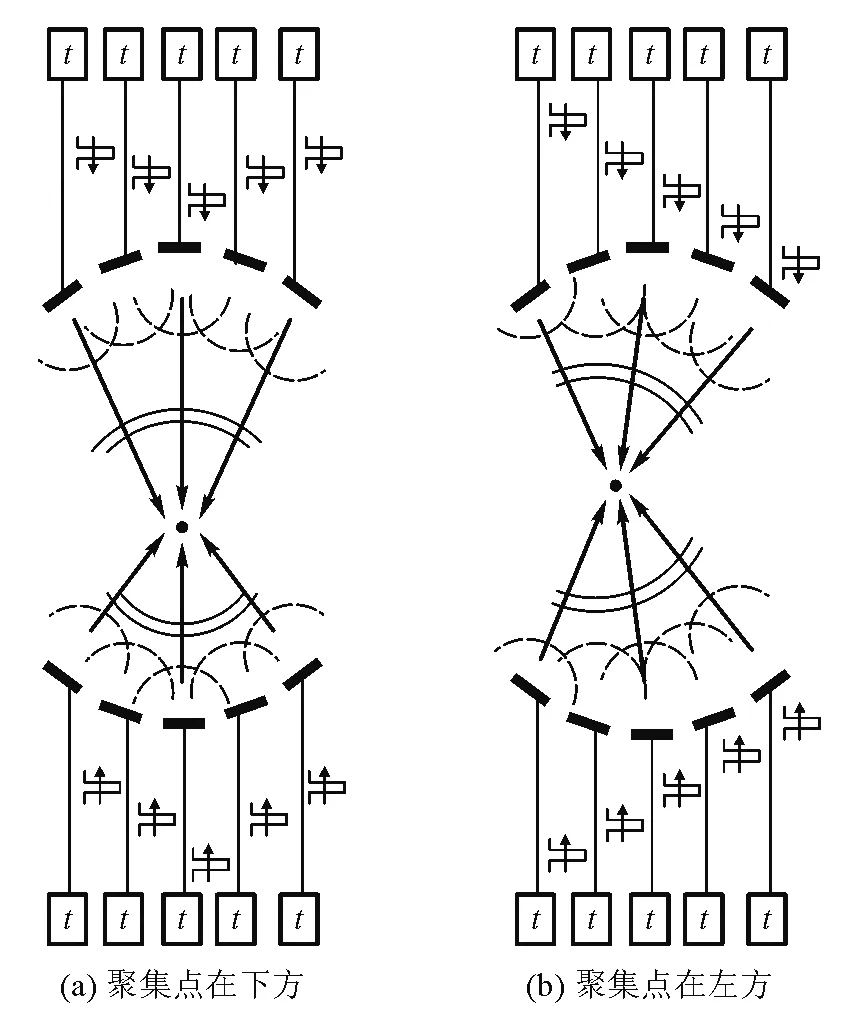
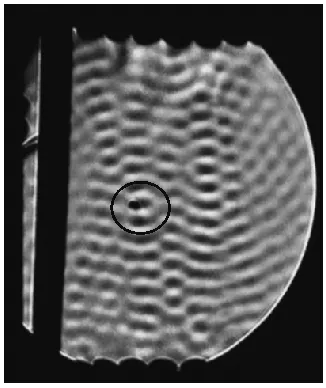
当超声波的频率为f时,超声波的单个周期时间为T,由于t可能会超过超声波的单个周期时间T,同时因为B相对A的信号提前t与延迟T-t的效果是一样的,为方便数据存储和信号控制,修正t使其始终在一个周期T之内,即使0 (4) 综上,有 (5) 其中n取合适的自然数使得|t|<1/f,通过控制每个换能器的时间t,就能使得换能器的超声波信号到达所设聚焦点时处于同一相位,进而实现聚焦点附近声场叠加,即相控聚焦. 图3 相控聚焦算法示意图 超声悬浮技术基本原理为:超声波传播过程中产生的声辐射力可以抗衡悬浮物体重力,使物体悬浮.在本文中,微粒悬浮的主要原理为超声驻波悬浮机理.超声驻波声场为两列振幅相同、频率相同、沿反方向传播的超声波相互叠加形成的具有一定空间能量分布的声场,由波腹和波节构成,总的波呈现驻留状态,故称为驻波. 假设在驻波声场中初始入射波和反射波的波动方程为余弦变化: (6) (7) 则叠加产生的驻波声场的波动方程为 (8) 式中,z1′为入射波中质点的振动位移,z2′为反射波中质点的振动位移,A0为超声波振动振幅,z为质点与入射面的距离,ω=2πf为超声波振动角频率(f为振动频率),k=ω/c0为波数(c0为声速). 驻波波腹(波峰)是对应声压的最大幅值,波节(波谷)对应声压的最小幅值(如图4所示). 图4 驻波图 超声驻波场中超声波的叠加会引起介质的疏密程度发生变化,产生声压.悬浮微粒一般悬浮于两波腹之间,即波节处.这是因为在波节处声压为0,当悬浮微粒受到重力的作用时,会相对于波节位置有微小的偏移,发生偏移时,由于波腹中声压的作用,悬浮微粒将会受到一个指向声压节点的回复力,使微粒回到原来的平衡位置.若悬浮微粒质量较大时,悬浮位置将会在波节处往下偏移一段微小距离,故悬浮微粒的悬浮位置取决于驻波波节位置. 声波是一种由物体振动产生的在介质中传播的疏密波,声波的传播实际上是介质中稠密和稀疏相互交替的过程,这样的变化过程一般可以用压强、密度、温度以及质点速度等变化量来描述.在流体介质中,声波的传播会引起流体压强的变化,就任一个体积元来讲,若体积元受到声扰动后压强由p0变为p1,则由声扰动产生的逾量压强为 p=p1-p0 (9) 称为声压[10],即声场中实际压强与环境背景压强的差值. 小幅度振动的介质所带动的微粒微小振动可近似看作简谐运动,声压的时间平均结果为0,无法使微粒起到“悬浮”作用[11].当超声波在流体介质中传播时,由于流体介质的非线性效应,使得声压的时间平均体现为对介质中的微粒产生持续的压力,使微粒“悬浮”. 建立波动方程可以更好地描述声扰动过程中声压p、质点速度v以及介质密度ρ等物理量之间的联系.为了简化运算,对空气介质进行近似,认为其是理想流体(没有黏性,绝热).一维的波动方程中包含运动方程、连续性方程与物态方程[10].运动方程描述p与v之间的关系为 (10) 连续性方程描述v与ρ之间的关系为 (11) 物态方程描述p与ρ之间的关系为 (12) 在这些方程中各声学量之间的关系是非线性的,为了得到用单一参量表示的声波方程,假设声波振幅较小,声波各参量以及其平方项以上的微量都可以在忽略的前提下对以上3个方程进行化简. (13) 其中c0表示平衡态的波速.将式(5)扩展到三维的情况,得到三维的声波波动方程为 (14) 声波入射到障碍物上产生一个与传播方向相同的平均压力称为声辐射力,这是描述声波在流体介质中传播规律时的一种二阶效应,是被忽略的声波的二阶小量.在声场中,物体表面的声辐射压力为 (15) 式中,p为声压,ρ0为悬浮介质密度,c0为声波在悬浮介质中的传播速率,v为声波传播时介质粒子的运动速率,<·>表示时间平均值.可以看出,声辐射压力与悬浮介质密度成正相关关系. 而科学家Gor’kov[12]从能量的角度着手,用声场平均势研究了悬浮介质与声场的相互作用. 在该理论中将悬浮微粒看作一个小球面体,得出悬浮小球在任意声场中的势能为 U=K1(|p|2)-K2(|px|2+|py|2+|pz|2) (16) (17) (18) 其中V表示悬浮小球的体积,ω表示超声发射频率,ρ0表示介质密度,ρp表示微粒密度,c0表示空气中的超声波速,cp表示微粒中的声速.声辐射力在Gor’kov声场平均势能中表示为 F=-U (19) 在z轴上,可表示为 (20) 相控聚焦超声波场的分布,具有肉眼很难直接观察的限制,为了更好的了解其声场的特性,引入COMSOL软件进行有限元分析,运用数值模拟的方式,获得相控聚焦声场的理论分布[13]. 本模型采用COMSOL中的压力声学模块的频域接口进行建模,求解声场的亥姆霍兹方程并进行数值计算. 超声换能器的单极域源Qn可以表示为 Qn= (21) 式中pt为总声压场,ρc为空气密度,ω=2πf为声波的角频率,c为声速,qd为偶极域源,但由于本模型中未设置偶极域源,因此此项为0.每个单极域源可以用三维狄拉克δ函数表示: Qn(z)=ωanδ(z-zn) (22) 式中zn是超声波换能器n的所在位置,z是空间中某一点的坐标,an表示单极域源流出的强度.把G设为亥姆霍兹方程的格林函数,及以下方程的解: (2+k2)G(x)=-δ(z) (23) k为由ω/c决定的波数,于是可获得方程的球面波的解为 (24) 凹球面双发射极超声阵列为多阵列结构,其任意点源r的声压p为 (25) 其中Pn为超声传感器输出功率,LN是每个延迟线的损耗因子,Df是远场方向性函数,dn是在自由空间中的传播距离,φn+kΔn表示在任意点源r处非线性超声波的相位,Δn是超声波传感器与聚焦点处的传播距离,φn是发射器相位,k是波数.式(25)的解由ρG和∑Qn的卷积得出 (26) 本研究的声压分布具有面对称性,因此,为了简化模型,降低计算量,提高计算速度和降低计算所需的内存要求,对实物模型进行降维处理,进行二维声场的数值模拟. 图5为根据本实验的实物装置所建立的二维模型,其中模型主体为两个半径为109.12 mm的凹球壳,各个独立的超声波换能器呈对称分布. 经过拆解本实验采用的TCT40-16T超声换能器,发现该超声换能器所用的振子表面并不是平的,而是中心比四周偏低的凹形,因此为了简便建立几何模型和符合超声波换能器振子表面的形状特点,设置换能器阵元形状贴合凹球形底座. 图5 COMSOL模型设置图 在COMSOL软件中,可以采用平面波辐射边界条件模拟无限边界或被完全吸收的情况,本模型四周为无限广阔的空间,由于超声波具有衰减快、易被吸收的特点,并且本装置超声波功率较小,装置空间较大,换能器紧密排列后形成多缝隙的空间,因此超声波反射的影响可忽略不计,所以本模型将所有边界都设置为平面波辐射边界条件,模拟无限边界或超声波在边界处被完全吸收. 图6 COMSOL边界条件设置图 为模拟聚焦声场的声场分布,采用COMSOL中基于振动有限元(FEM)的接口进行有限元分析. 如图7所示,为了得到较为精确的声场分布和运算速度,网格尺寸定为波长λ的1/6. 图7 COMSOL网格设置图 如图5所示,上凹球壳中从左到右分别是阵元1到阵元6,下凹球壳中从左到右分别是阵元7到阵元12. 设坐标原点为球壳中心,球壳半径为109.12 mm,则各阵元坐标见表1. 表1 COMSOL仿真阵元坐标设置 根据实验装置所处的环境设置声速参数为343 m/s.以阵元1信号作为基准信号,基于各阵元相对时延t的计算,在COMSOL仿真过程中超声波阵元信号设置需要用到各阵元的相对相位Δφ,当超声波频率为f时,各阵元相对时延t与相对相位Δφ有如下换算关系: (27) 其中T=1/f,本文中f=40 kHz,故可计算得到各阵元的相对时延和相对相位如表2所示. 表2 各阵元的相对相位和相对时延 纹影系统用到的光学器件一般是透镜或反射镜.对于本文所要研究的声场,其区域较大,若使用透镜纹影系统,需要使得透镜表面r/2直径范围内有高灵敏度的工作,这对于透镜的要求较高,且纹影对象比较微弱,难以用肉眼直接进行观察,因此透镜上面的瑕疵以及像差很可能会遮盖住纹影对象,对纹影结果造成影响[14]. 故本研究中采用使用反射镜的单反射式纹影装置对相控聚焦超声波场进行观察,相对于Z型光路,单反射纹影装置结构简单,实验可重复性强,虽然会因为发射光线和反射光线的不重合,导致一定程度的图像失真,但其光线经过二次折射,灵敏度可以达到Z型反射纹影光路的两倍[15]. 最后将纹影结果与COMSOL数值仿真结果进行对比,结果得出可视化相控聚焦声场与模拟声场之间有很好的一致性,证实了相控聚焦原理设计方式的合理性与其价值. 纹影装置细节如图8所示,该装置由一个焦距为750 mm的凹球面反射镜、LED光源、小孔遮光片以及用于采集图像的手机摄像头组成(手机型号为HUAWEI mate10 pro). 当LED光源经过带小孔的遮光片时,可以将其认为点光源,点光源发出的光经过相控聚焦声场后,声场的声压分布会对周围空气介质密度产生影响,从而改变空气折射率,即 n-1=kρ (27) 其中n为介质折射率,ρ为介质密度,两个物理量通过Gladstone-Dale系数联系起来[16]. 图8 单反射式纹影实验图 光线经过超声波场后经反射镜反射将再次经过声场,其中未被折射过的光线会在反射镜的两倍焦距处聚集,而经过折射的光线将会偏离聚焦点,调整手机摄像头的位置,使光线聚焦点在镜头内同时尽可能靠近镜头边缘. 由于手机摄像头的尺寸限制,其边缘部分可以对偏折光线起到过滤作用,最后采集到聚焦点附近的图像,得到声场的纹影图. 此外,调整手机摄像头与点光源的位置使点光源与光线聚焦点尽可能地靠近,这样可以大大减小因发射光线和反射光线的不重合所产生的图像失真. 同时因为手机摄像头尺寸小,所以手机摄像头与点光源之间的距离可以比大尺寸摄像机与点光源之间的距离更近,因而使用手机摄像头或者小尺寸摄像机在图8所示的纹影法中得到的图像会比使用大尺寸摄像机得到的图像失真更小. 将实验所得到的相控聚焦超声波场纹影图像与COMSOL仿真结果进行比较. 聚焦点COMSOL仿真各换能器坐标和相位延迟信息由表1和表2给出. 从图9可以看出,纹影图像与COMSOL仿真图中聚焦点的位置基本一致,由于摄像机设备在拍摄时会有一定的延时效果,所以拍摄后得到的纹影图像是时间平均后的结果,声场的某些细节经时间平均后被减弱. 考虑到时间平均对于纹影图像的影响,在实验中将LED光源换成与超声波频率相同的频闪光源(40 kHz),即光源每次亮灯时对应的声场信息是相同的,故摄像机时间平均后得到的图像为相同的声场信息的叠加,解决了声场细节被减弱的问题,如图10所示. 光源经过改进以后,声场的基本信息可以很好地被纹影法重现. 从定性的角度看,超声波聚焦点位置与理论计算位置基本一致. 通过摄像头的实时拍摄,可以看出当聚焦点位置改变时,微粒位置会随着聚焦点变化而变化,实现对微粒的操控. 本文基于先前研究中平面阵列相控聚焦超声波场的缺点,将相控聚焦算法应用于双凹球壳阵列. 经测试,该装置产生的声场可以稳定悬浮微粒且实现悬浮微粒的全三维移动. 然后,基于各超声波阵元信号的相对时延、声压、声辐射力等理论基础,借助COMSOL Multiphysics多物理场仿真软件进行仿真模拟,发现在相控聚焦点附近可形成类似驻波的声场,并且可以通过改变各阵元间的信号时延实现聚焦点的移动,同时聚焦点附近波节处还可以稳定悬浮多个聚乙烯微粒,通过声场移动可带动其进行三维移动. 接着用单反射式纹影法实时观测双凹球壳阵列在不同聚焦点时产生的声场,并与COMSOL Multiphysics软件中的仿真结果进行比对,发现两者基本吻合,以此验证了相控聚焦原理在控制声场三维移动的理论的正确性.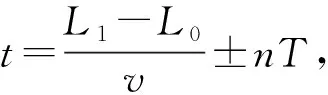
1.3 超声驻波悬浮理论
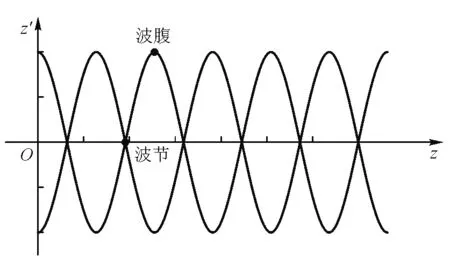
2 声学理论
2.1 声压
2.2 声波波动方程
2.3 声辐射力
3 COMSOL 声场仿真
3.1 COMSOL理论模型[2]
3.2 COMSOL几何模型建立
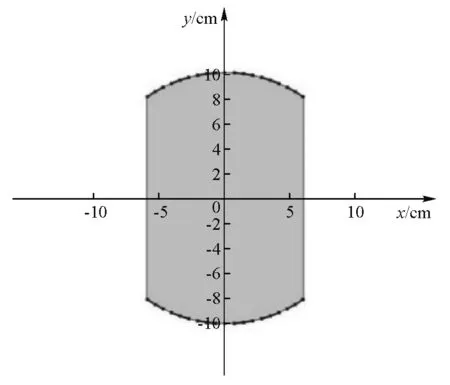
3.3 COMSOL边界条件设置
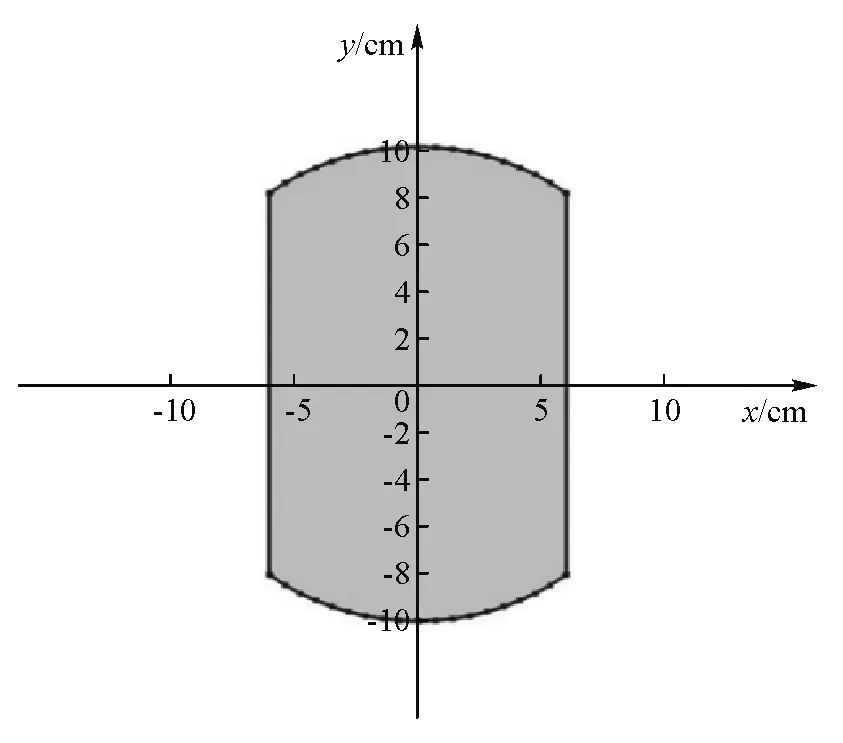
3.4 COMSOL有限元分析
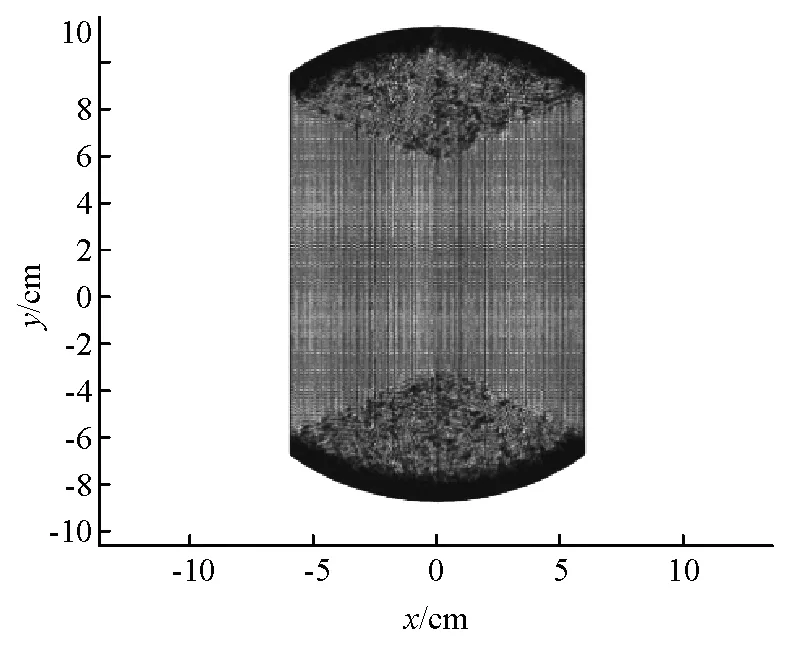
3.5 COMSOL超声波阵元信号设置
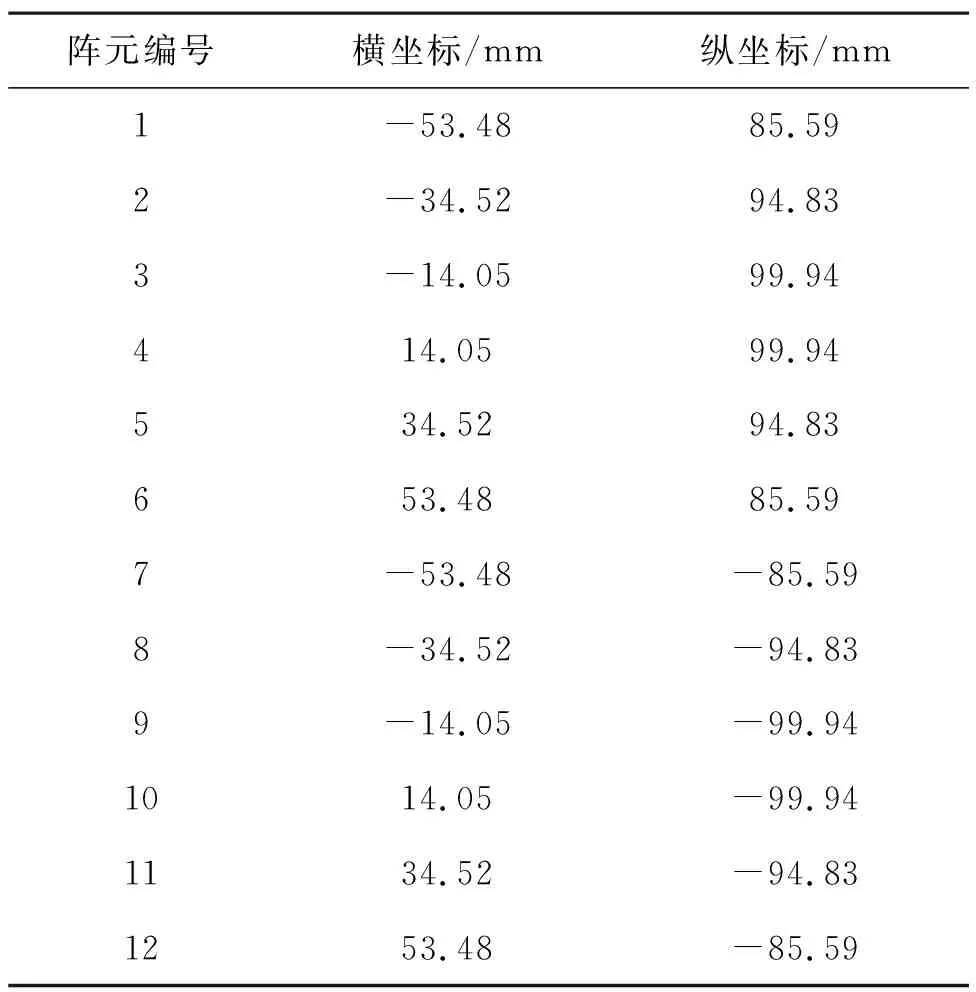
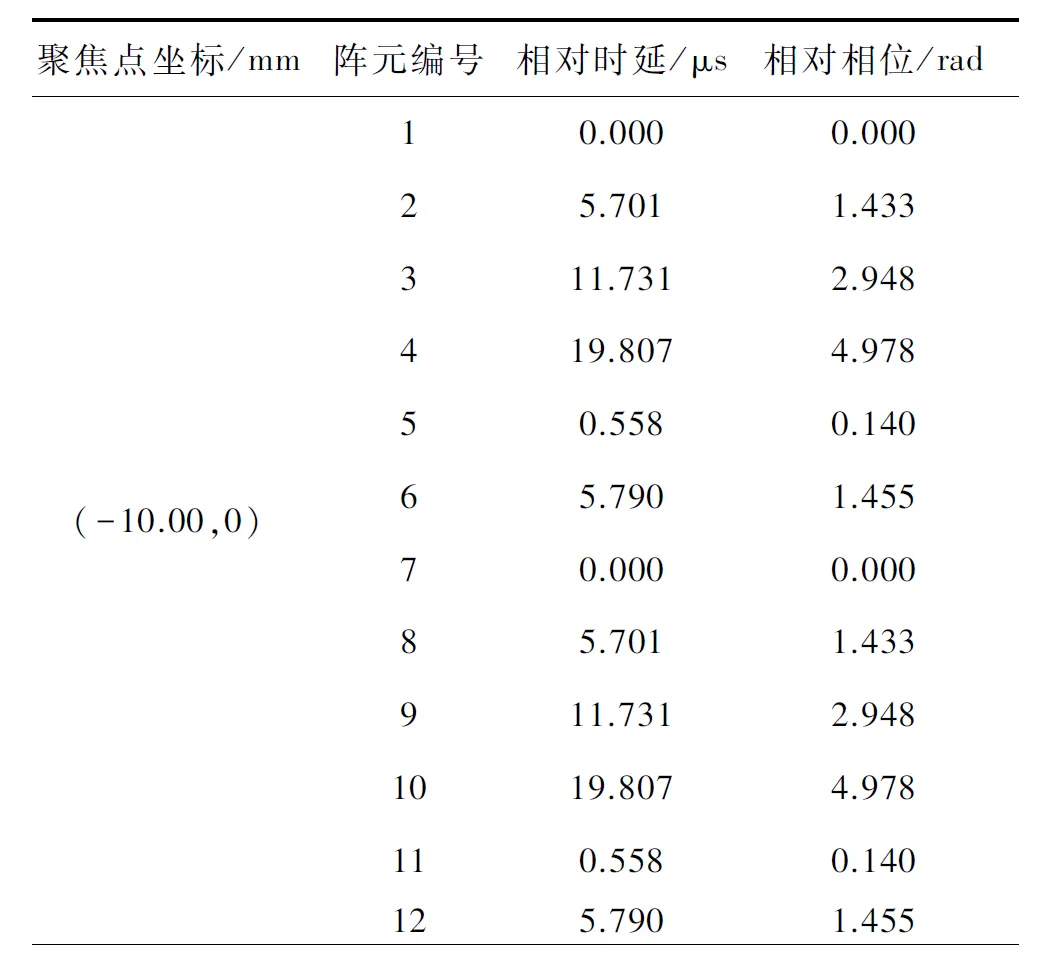
4 纹影法观察超声波声场
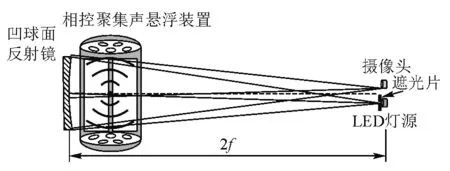
4.1 单反射式纹影法
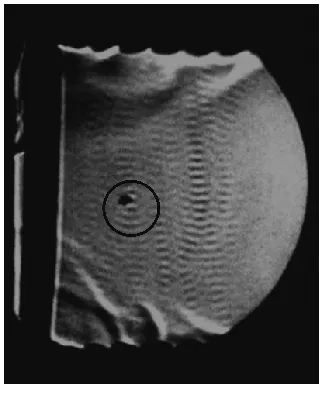
4.2 纹影法结果
5 结束语

