正交各向异性层合板壳耦合结构的能量传递特性

李 翱， 陈海波， 钟 强， 王 幸

(中国科学技术大学 近代力学系 中国科学院材料力学行为与设计重点实验室，合肥 230026)

板壳结构广泛应用于汽车、船舶、航空航天等工程领域，其中很多采用的是复合材料层合结构，且在许多服役状态下都需要分析其高频振动响应。板壳高频振动的一个显著特征是结构变形的波长远小于结构的整体尺寸，这意味着通过标准有限元建模计算成本高，非确定性因数较为敏感，因此计算鲁棒性不强[1]。为了避免这两个问题，多种能量方法已被提出，其中最流行的是统计能量分析(statistical energy analysis,SEA)以及它的扩展方法能量有限元法(energy finite element method,EFEM)、能量辐射传递法(radiative energy transfer method，RETM)等[2]，它们大多基于弹性波在结构中的运动进行研究[3-4]。弹性波在传播过程中，如遇结构不连续处，即多结构耦合处以及边界处，会产生折反射且伴随着入射功率在不同波场形式间的重新分配，这也意味着能量的重新分配。研究耦合处波的传递是一个传统问题，它体现了能量在耦合处的分配，而能量传递系数则从数值上量化了这种分配[5]。因此，讨论弹性波在结构不连续处的透反射情况，研究能量在板壳结构中的耦合传递系数是极为必要的，它是计算系统耦合损耗因子(coupling loss factor,CLF)的关键[6]。实际上采用功率流有限元等能量方法研究耦合结构的振动传递特性时，能量传递系数的计算是必须首先要解决的关键问题之一[7-8]。

目前，对耦合结构能量传递特性的研究主要针对板结构，如Le Bot推导了多板沿一条边界耦合的能量传递系数，Langley等[9]针对多板耦合于梁的系统，研究了弹性波的传递特性。江民圣等[10]对任意夹角的耦合板能量传递系数进行研究，讨论了板厚及激励频率对L型耦合板能量传递系数的影响。葛月[11]计算了耦合板的能量传递系数，并将其应用于对应耦合结构的能量边界元分析中。Yan等[12-13]对复合材料板的耦合能量传递系数进行推导,然后基于此对系统进行能量有限元分析。Xie等[14]计算了只考虑弯曲波时正交各向异性加筋板的能量传递系数，对耦合系统的弯曲振动能量有限元进行了验证分析。

曲板与平板耦合、曲板与曲板耦合常见于飞机机身结构中，例如，机翼-机身连接、地板-机身连接，但对于弹性波在此类耦合系统中的传递特性研究较少。Langley计算了弹性波在曲板耦合系统中的能量传递系数和耦合损耗因子，Tso等[15]研究了波在封闭圆柱壳与肋板周向耦合系统中的传播，但均未涉及复合材料层合结构。对层合曲板的研究目前主要针对其单个子系统的波数、模态密度和传声损失[16]，只有Lee讨论了波在复合材料圆柱壳轴向和环向上的传播。复合材料层合结构在实际工程中的应用日益广泛，占比也越来越重，复合材料耦合结构中的能量传递系数计算已成为耦合系统分析必须解决的基本问题之一[17]。简言之，研究波在复合材料层合板壳耦合系统中的能量传递特性，极具工程意义。

本文基于复合材料的力学性能对层合板壳结构的平衡微分方程进行推导，进而根据波法的位移假设求解波数曲线，然后借鉴Langley提出的波动刚度矩阵方法对正交各向异性层合板壳耦合结构的能量传递系数进行求解，并在此基础上计算了层合板壳耦合系统的耦合损耗因子。本文的工作完善了层合板壳耦合结构高频振动相关理论，为后续进一步进行能量预报奠定了基础。

1 正交各向异性层合板壳的平衡微分方程

平衡微分方程是研究层合结构耦合系统能量传递特性的关键，本文基于薄壳理论[18]和经典层合板理论[19]推导正交各向异性层合板壳的平衡微分方程。

1.1 层合板壳的应力应变关系

图1为正交各向异性单层板单元体。图1中:x-y为偏轴坐标系;1-2为材料主方向即正轴坐标系;x轴与材料主方向1之间的夹角α为复合材料单层方向角。

图1 一般正交各向异性板的两个坐标系

其正轴模量矩阵为

(1)

其偏轴模量矩阵为

(2)

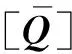
(3)

对于一般复合材料层合结构如图2所示。

图2 一般层合板壳的几何结构

其内力-应变关系为

(4)

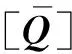
(5)

式中:N、M为内力矩阵;Nx、Ny为轴力;Nxy为切向力;Mx、My为弯矩;Mxy为扭矩;ε为中面应变矩阵;κ为中面曲率矩阵。

1.2 层合板壳的平衡微分方程

对于图3所示的层合壳结构。

图3 环向开敞层合柱壳单元

其中面应变和曲率如下

(6)

式中:u、v、w为中面位移;R为柱壳的曲率半径。通过式(5)和(6)可求解内力矩阵式(4)，结合式(4)和式(7)

(7)

便可计算出剪力Qx、Qy及加上扭矩等效剪力后的总剪力Qxt、Qyt。

将内力与剪力代入柱壳微元体的力平衡方程

(8)

式中,qx、qy、qz为层合柱壳所受载荷在x、y、z三个方向上的分量。

得层合柱壳的平衡微分方程

L(u)=0

(9)

(10)

(11)

(12)

2 正交各向异性层合板壳耦合能量传递

针对各向异性结构无法利用亥姆霍兹方程对平衡微分方程进行解耦，这里直接基于波法给出位移表达式，由Snell折反射定律[20]得波数在耦合边界上的投影相等，将位移代入平衡微分方程求解特征值和特征向量，最后基于耦合处力的平衡条件和位移连续性条件,对能量传递系数进行求解。

2.1 正交各向异性层合板壳波数曲线

在图3中，考虑曲率半径的影响，对于x边界，坐标y为常数，其转角为v/R-∂w/∂y。所以四个边界位移可以写成

d=S(u)

(13)

S是一个4×3的微分算子，其非零元素如下

(14)

同理，对应的四个边界力Nyx、Ny、Qyt、My可以写成如下形式

t=T(u)

(15)

T的元素如下

(16)

(17)

(18)

(19)

基于波法，位移矩阵u的解可以假设为以下形式

u=αe-ikxx-ikyy+iωt

(20)

式中:ω为圆频率;kx=kcosθ、ky=ksinθ分别为波数k在x和y方向的分量;θ为波的入射角;α为位移的复波幅向量。将式(20)代入平衡微分方程式(11)得

H(kx,ky,ω)α=0

(21)

H是一个3×3的矩阵，给定ω，可以计算出相应的波数曲线。如图4所示，曲线1，2代表弯曲波，曲线3代表剪切波，曲线4代表纵波(也叫拉压波)。对层合柱壳只有当ω增大到一定值时才会出现纵波，否则只存在剪切波和弯曲波。

2.2 耦合系统的能量传递系数

令λ=-iky，式(21)可以写为

H(kx,λ,ω)α=0

(22)

由Snell定律可知，kimcosθim=kjncosθjn(m、n为结构编号；i、j=1,2,3,4为图4中波的编号)，即每个子结构中的波沿耦合边界具有相同的运动，它们在x方向的波数分量kx相等。 当给定ω和kx，沿y轴正向可以解出四个有效特征值λj，及对应的四个特征向量αj。每个λj值对应一个有效波，即位移受多个波场的影响，且每个λj所对应的单位幅值的波的功率为

(23)

其中，Sj和Tj分别由式(14)和式(16)～(19)给出，式中∂/∂x由-ikx替代，∂/∂y由λj替代。一旦四个有效λj值确定，位移向量便可以写成以下形式

(24)

式中:Aj对应第j个有效波的幅值;A0为入射波的幅值;λ0,α0为入射波在式(22)中的解。联立等式(13)和(14),则边界位移可以写成

d=P1A+d0

(25)

t=P2A+t0

(26)

联立式(25)、(26)，边界位移和力的关系式如下

(27)

式中:K为结构的波动刚度矩阵;f为入射波引起的动力载荷。

在图5所示的半无限层合板壳耦合系统中，第n个子系统在连接处的切线方向与全局坐标轴yg的夹角为Φn，其局部坐标系中的耦合处边界位移为dn，边界力为tn。 设全局坐标系中连接处的位移dg，合力为tg。

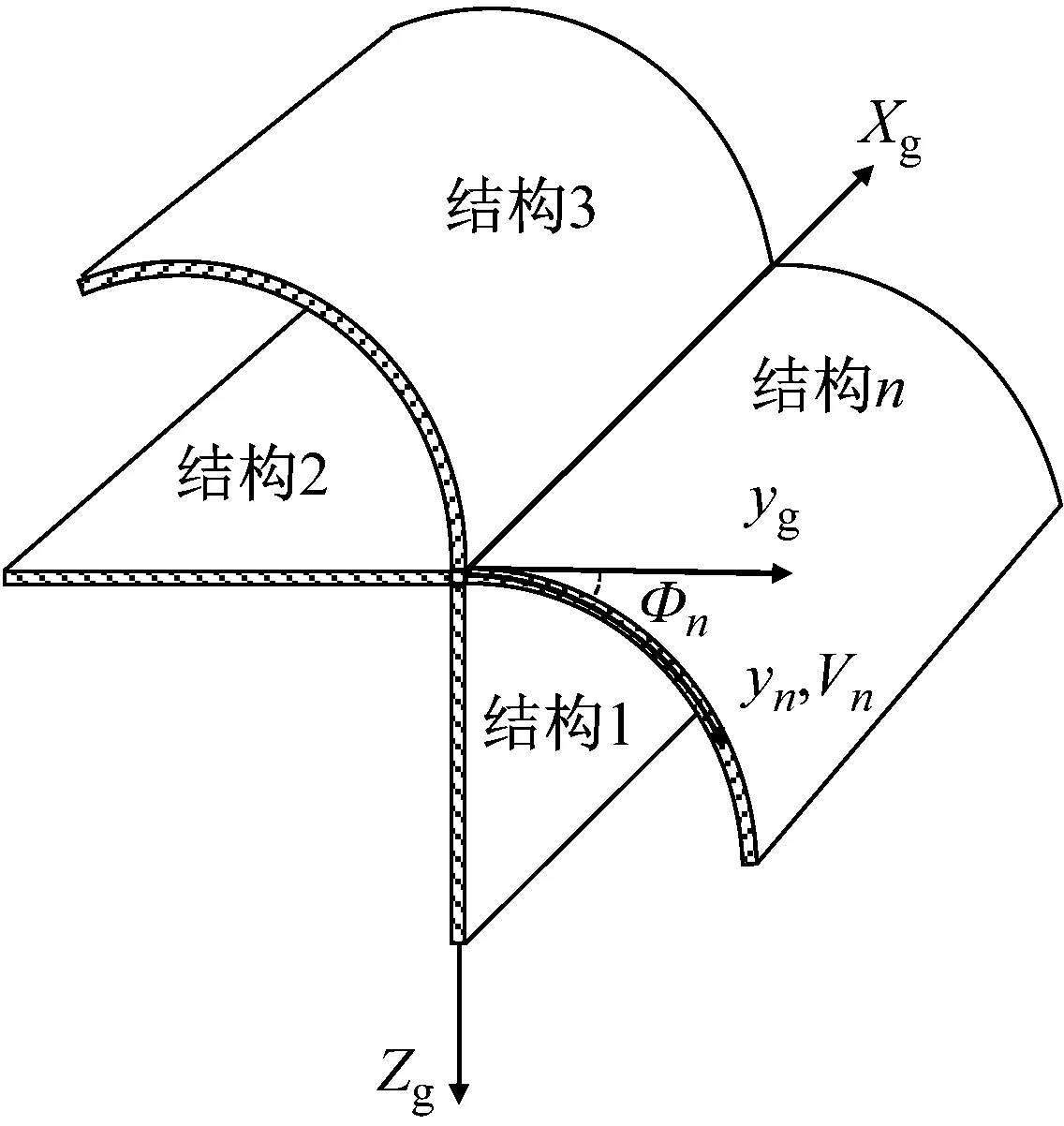
图5 半无限层合板壳耦合系统示意图

根据耦合处位移连续性，dn与dg的转换关系如下

(28)

(29)

式中,Rn为坐标转换矩阵。根据耦合处力的平衡可得

(30)

式中,N为耦合系统中子系统总数。根据式(27)可知tn=Kndn-fn。当入射波作用在第m个子系统上时，式(30)可写为

(31)

(32)

所以产生的各个波在传递时携带的能量为

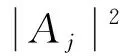
(33)

式中,Pyj由式(23)给出。从而可以计算出入射波传递到结构耦合处所产生的各个波的能量传递系数为

τijmn=Pijmn/Pim

(34)

式中:Pim为在结构m中入射i型波的功率;Pijmn为结构m中的i型波传递到结构n中产生j型波的功率。当m≠n时，τijmn表示结构m中的i型波传递到结构n中产生j型波的能量透射系数；当m=n时，τijmm表示结构m中的i型波经过耦合处反射到结构m中产生j型波的能量反射系数。所有的能量传递系数总和为1。

2.3 耦合损耗因子CLF

式(23)代表波沿y方向传播的功率流，同理可以计算出波沿x方向传播的功率流Pxj。所以能量传播角为

θe=arctan(Pyj/Pxj)

(35)

又总能量密度

(36)

所以波群速度为

(37)

方向为波数曲线的外法线方向，如图6所示。

图6 波与能量的传播方向

群速度在y方向和θ方向的投影分别为

cgy=cgsinθe,cgθ=cgcos(θ-θe)

(38)

对于面积为Lx×Ly的层合板壳结构，每个模态频率对应的网格面积为π2/(LxLy)，所以图6所示波数曲线与坐标轴围成的面积包含的模态数为

(39)

模态密度为

(40)

又波速c=ω/k，式(38)中θ方向的波群速度也可以由cgθ=dω/dk得到，所以式(40)可变换为如下形式

(41)

所以给定ω时，模态密度随入射角的变化为

(42)

相应的模态能量为

(43)

式中，E为结构振动总能量。所以在整个耦合边界上，由结构m中入射i型波传递到结构n中转换为j型波的总能量流为

(44)

式中,Ljunction为耦合边界的长度。

在SEA理论中，qijmn=ηijmnωEim，ηijmn为耦合损耗因子。所以，对于图5所示的线耦合结构，由式(44)可计算出能量传递系数和耦合损耗因子之间存在如下关系

(45)

式中,τijmn由式(34)给出。

当我们将能量传递系数应用于耦合系统的能量预报时，基于混响场假设需要对能量传递系数进行如下平均

(46)

当材料为各向同性时，式(46)便可简化为我们常见的标准各向同性混响场平均传递系数计算公式

(47)

3 数值算例分析

3.1 频散曲线

以石墨/环氧树脂复合材料为例，其材料参数如表1所示。计算图3所示的层合柱壳的频散曲线并与Ghinet的结果进行对比验证。各层材料方向角:[0°/45°/-45°/90°/-45°/45°/0°]。每层材料厚度为2 mm，单曲率环向开敞层合柱壳的曲率半径为2 m。厚径比为0.007，小于0.05，可视为薄壳。

表1 石墨/环氧复合材料参数

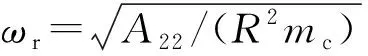
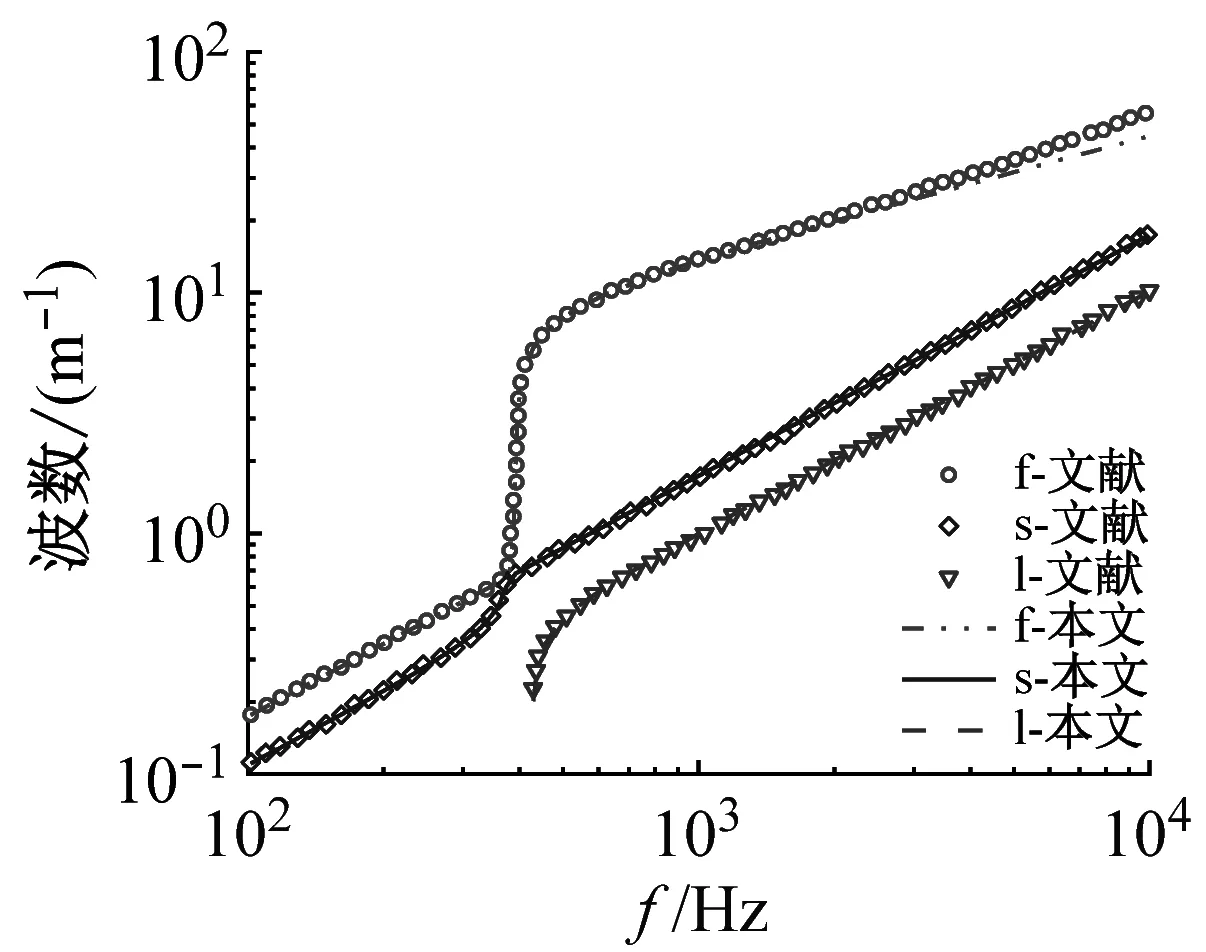
(a) θ=0°

3.2 模态密度

本节以三层碳纤维/环氧树脂复合材料为例(每层铺设角度如图8所示)，其材料参数如表2所示。分别就层合板和环向开敞层合柱壳的模态密度进行计算，并讨论两者的异同之处。每层材料厚度为1 mm,面积为1 m×1 m,柱壳的厚径比为0.01。

图8 三层碳纤维/环氧方向示意图

表2 碳纤维/环氧复合材料参数

图9中，在频率较低时，环向开敞层合柱壳的弯曲波与剪切波模态密度要比相同表面积和厚度的层合板小，此时层合柱壳不存在纵波。曲率的引入相当于增大了层合柱壳的刚度，使得其模态数减少，即出现曲率的刚化效应，这与各向同性柱壳的特性类似。

(a) 弯曲波

随着频率增加，层合柱壳的弯曲波及剪切波模态密度也随之急剧增加，并超过相对应的层合板模态密度。当频率增大至环频率fr=1 698 Hz时，层合柱壳的纵波开始出现，且远大于层合板的纵波模态密度。在环频率fr附近层合柱壳的弯曲波和剪切波模态密度出现峰值，此后层合柱壳的模态密度开始向层合板过渡，随着频率的增大两者趋于一致。对于层合板的弯曲波，其模态密度基本不随频率变化，保持在0.041 67 (rad·s-1)-1,而层合板的面内剪切波和纵波模态密度则随频率呈线性增加，即式(41)中对应的面内波速度与群速度的乘积关于入射角的积分在频率增大到一定值后开始收敛。此外，从以上三个对比结果来看，曲率半径对剪切波的影响相较弯曲波和纵波小。

3.3 能量传递系数

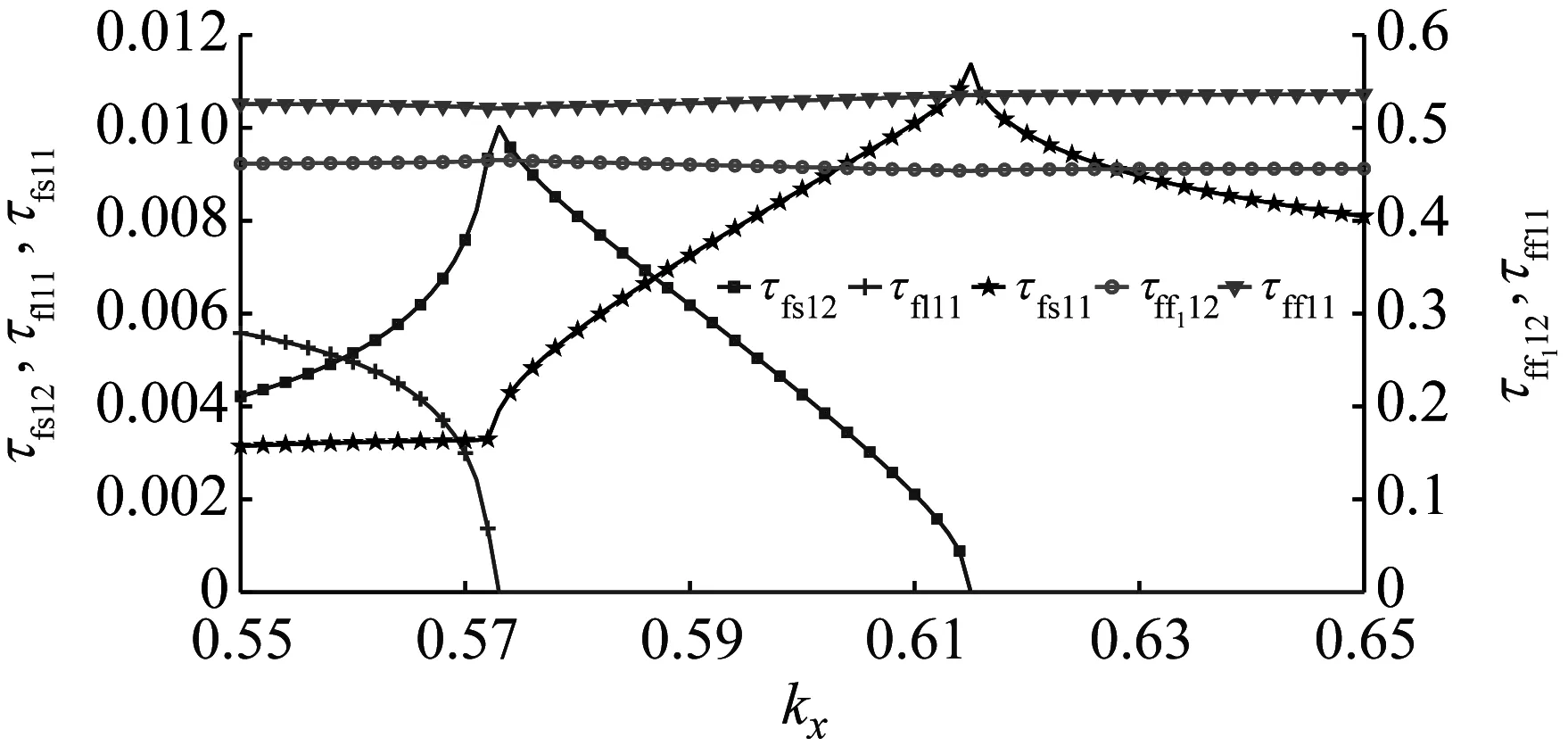
以层合板与环向开敞层合柱壳沿x轴耦合为例，计算在层合板上分别入射弯曲波、剪切波、纵波时的能量传递系数,如图10所示。耦合角度φ=90°，φ=|Φm-Φn|，结构都为三层碳纤维/环氧树脂复合材料，每层材料厚度为1 mm，材料方向角为[0°/90°/0°]，结构2的厚径比为0.01。激励频率4 000 Hz，结构1，2的波数曲线分别如图11和图12所示。两个结构的临界值kx1、kx2基本重合，kx1=3.252 3为纵波的临界值，kx2=11.930 8为剪切波的临界值。kx4为结构2弯曲波在x方向的最大波数值，即曲线1，2的分界点。能量传递系数随kx的变化情况如图13所示。

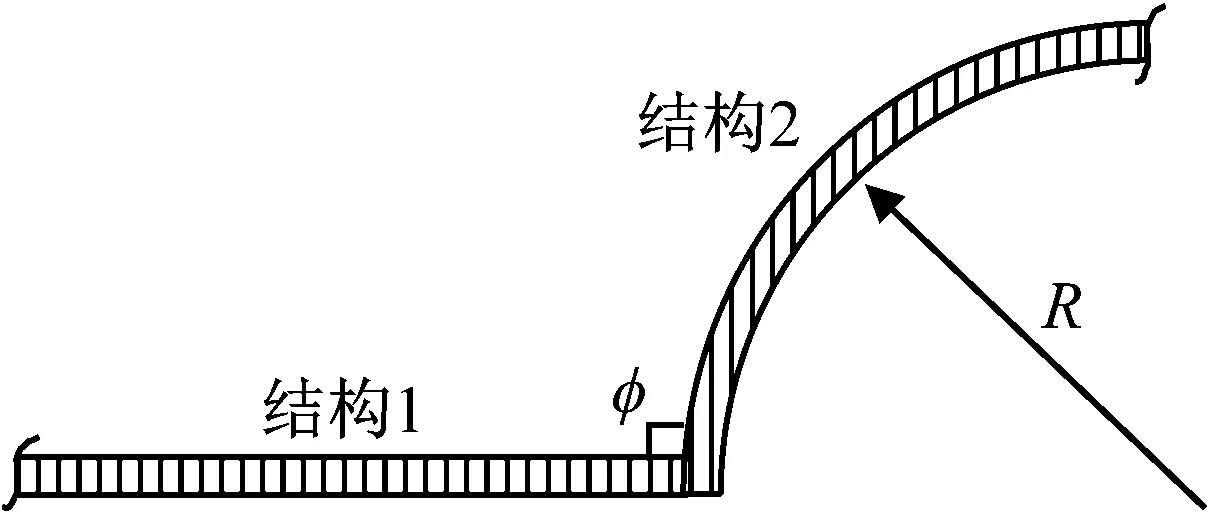
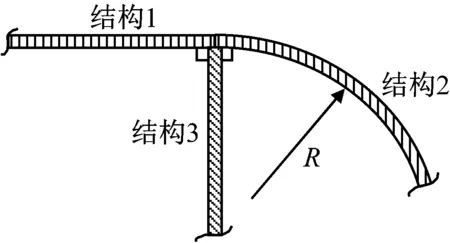
图10 层合板壳耦合系统

图11 结构1的波数曲线

图12 结构2的波数曲线

(a) 入射弯曲波

图13(a)中入射波为弯曲波，为方便起见，采用双y轴坐标进行绘图，后续部分绘图亦如此。f1、f2分别为图12中结构2的弯曲波1、2。当kx接近kx1(θ=88.13°)时，纵波的透射和反射能量系数τfl12、τfl11快速衰减并在kx1处完全终止，而弯曲波能量系数处于相对平稳状态。与此同时开始发生弯曲波向剪切波的波型转换，并随着kx的增大这种波型转换逐渐增强。当kx增大到kx2(θ=83.09°)时，剪切波终止，仅反射和透射弯曲波，且反射强于透射。当kx为kx3=45.496 8(θ=58.16°)时，对应两个不同的ky，即开始在两个不同的方向同时透射弯曲波τff112、τff212(当频率较大时不发生此现象)。在kx4=52.798 7(θ=42.87°)以后，不发生透射，为全反射状态。

图13(b)中入射波为剪切波，当kx

图13(c)中入射波为纵波，可以发现整体上反射回层合板内的纵波占主导地位。当入射角较大时，透射波以弯曲波为主，在很大范围内维持平稳。弯曲波的反射系数与透射系数变化规律一致，但从右侧坐标刻度可以看出弯曲波反射系数很小。随着kx的增大，反射的纵波逐渐衰减，当kx>3后，反射回层合板内的剪切波、透射到层合柱壳内的剪切波和纵波先后到达峰值，且峰值点依次增大。另一方面，也反映出当入射角较小时，透射能量占比较大，以面内波能量为主。

从图14中可以看到能量传递系数之间满足互易性，即τijmn=τjinm。

图14 能量传递系数满足互易性

综上所述，对于耦合角度为90°且材料相同的层合板壳耦合系统，在连接处波的能量反射强于透射。另外，可以发现三个图中的能量传递系数总和恒为1，满足保守耦合系统的能量守恒，这从侧面证明了计算的正确性，且能量传递系数满足互易性。

将图10所示耦合结构的材料退化为铝合金进行计算，铝合金参数如表3所示。所得结果如图15所示，这与Langley的计算结果图10完全一致。

表3 铝合金材料参数

图15 在结构1上入射弯曲波，ω=3 076.8 rad/s

本文还计算了如图16所示三结构耦合的情况，结构材料及厚度与图10所示的算例一致。激励频率为4 000 Hz，以在结构1上输入弯曲波为例，对各子系统间的能量传递系数进行计算。如图17所示，能量传递系数总和恒为1，同样满足了保守耦合系统的能量守恒。

图16 三结构耦合

图17 能量传递系数

3.4 耦合角度和激励频率对CLF的影响

本节在3.3节分析的基础上计算系统的耦合损耗因子，层合板和柱壳的面积尺寸均为1 m×1 m，分别讨论其随耦合角度和频率的变化。

图18为耦合损耗因子随耦合角度的变化，频率为4 000 Hz。如图18(a)所示入射波为弯曲波，以ηff11和ηff112为主。当φ≤15.75°和φ≥150.8°时，ηff11随耦合角的增大而减小，当15.75°<φ<150.8°时，ηff11整体趋势单调递增，透射到层合柱壳中的弯曲波耦合损耗因子ηff112变化情况则与之相反。并且在此频率下，出现弯曲波多角度透射，ηff212分别在耦合角φ=4.5°、171°出现峰值，耦合角接近90°时，其值较小。此外与面内剪切波、纵波对应的耦合损耗因子占比很小，剪切波的透反射耦合损耗因子ηfs12、ηfs11大于纵波的ηfl12、ηfl11，在0°～180°间都出现三个极值点，且在0°～180°值为0。

(a) 入射弯曲波

如图18(b)所示，入射剪切波时，以ηss11和ηss12为主。 随着耦合角度的增加ηss12先急剧下降后缓慢增加，在61.2°到达最小值，在180°值最大，此时除ηss11外其余耦合损耗因子近似为0。耦合角度为0°时，面内波之间存在波型转换，不存在面内波到离面弯曲波的转换。随着耦合角度的增加，ηsl12逐渐减小至0，ηsl11占比最小，ηss11先增后减在28.8°～133.2°之间占比最大，ηsf11、ηsf112存在两个波峰，且先后在75.6°和79.2°达到最低。

如图18(c)所示，入射纵波时，可以发现各耦合损耗因子的变换情况与入射剪切波时类似，当φ≤18°和φ≥147.6°时以ηll12为主，其余耦合角度以ηll11为主，且ηlf112较大占比仅次于ηll11。

另外还发现无论耦合角度如何变化耦合损耗因子的总和都恒为定值，且入射弯曲波时耦合损耗因子比入射剪切波及纵波时小，即入射弯曲波时层合板壳之间的耦合作用明显弱于入射面内波时的情况，这与各向同性材料耦合结构的规律一致。

图19给出耦合损耗因子随激励频率的变化，耦合角度φ=90°保持不变。从图19三个结果图来看，耦合损耗因子变化较为复杂的区域大致集中在5 000 Hz以前，且在这区域多数占比较大的耦合损耗因子衰减较快，在5 000 Hz以后衰减较为缓慢。当频率低于环向开敞层合柱壳的环频率fr=3 032.5 Hz时，不存在透射的纵波耦合损耗因子。

如图19(a)入射弯曲波时，当频率大于fr时，ηfl12开始出现随后趋于稳定，ηfs12也开始出现，并在6 760 Hz处出现突变，随后缓慢递减。ηfl11基本保持恒定值，ηff212存在较大波动且主要集中在环频率之前。总体上以弯曲波的透反射耦合损耗因子ηff11和ηff112为主，且ηff11占比最大。

入射剪切波时，如图19(b)所示，主要以ηss11、ηss12、ηsf112为主，且反射的耦合损耗因子占比同样大于透射。入射纵波时，如图19(c)所示，ηll11全程占主导地位。入射面内波时，耦合损耗因子的曲线较为光滑，而入射弯曲波时，曲线存在波折。

整体而言无论入射何种波，耦合损耗因子总和伴随频率增大而逐渐衰减，频率越大衰减越缓慢。简言之，频率越大子系统间的耦合作用越弱，且入射弯曲波时层合板壳之间的耦合作用同样明显弱于入射面内波时，这同样与各向同性材料耦合结构的规律一致。

3.5 不同铺设方式对能量总透射系数的影响

前文已对各种波的能量传递系数进行了详细讨论，故本节重点分析铺设方式对总的能量传递的影响。同样以3.3节中层合板与环向开敞层合柱壳90°耦合为例，设置结构1的材料铺设角度为[0°/0°/0°]保持不变。分别入射弯曲波、剪切波和纵波，探究结构2在不同铺设方式下对能量总透射系数的影响。结构1为三层碳纤维/环氧树脂复合材料，结构2为四层碳纤维/环氧树脂复合材料，选择对称铺设为[α/-α/-α/α],反对称铺设为[α/-α/α/-α]，铺设角度为45°，每层材料厚度都为1 mm。

图20～图22计算了两种铺设方式下，三种入射波的能量总透射系数。从图中可以发现，虽然不同铺设方式对弯曲波能量的透射较面内剪切波和纵波的影响略大，但两种铺设方式的计算结果整体来看相差甚小，即能量总透射系数对铺设方式的敏感度较低。计算还表明，铺设角度为30°和60°时的计算结果与45°结果的规律相同。

4 结 论

本文以正交各向异性层合板和柱壳为研究对象，基于薄壳和层合板理论推导了位移为基本变量的平衡微分方程，通过计算环向开敞层合柱壳的频散曲线与已有研究进行对比，验证本文理论推导的正确性。然后根据波动刚度矩阵方法对耦合系统间的能量传递系数进行求解，并结合模态密度推导耦合处的耦合损耗因子(CLF)。数值算例分析表明：

(1) 在频率较低时，曲率的引入相当于增大了层合柱壳的刚度，使得其模态数减少，即出现曲率的刚化效应。但在环频率以后，随着频率的增大层合板与柱壳的模态密度趋于一致。此外曲率半径对剪切波的影响相较弯曲波和纵波小。

(2) 能量传递系数总和恒为1，满足保守耦合系统的能量守恒，且能量传递系数具有互易性。对于材料相同的层合板壳90°耦合系统，在连接处波的能量反射强于透射。此外发现能量总透射系数对铺设方式的敏感度较低。

(3) 耦合损耗因子CLF的总和不受耦合角度影响，且随频率增大而逐渐衰减，当入射弯曲波时耦合损耗因子比入射剪切波及纵波时小，即入射弯曲波时层合板壳之间的耦合作用明显弱于入射面内波的时候。