旋叶式压缩机多刚柔耦合建模与叶片动态接触激励分析
李俊潇, 何泽银, 陶平安, 邓 刚, 马丽英
(1.重庆交通大学 机电与车辆工程学院,重庆 400074; 2.重庆川仪速达机电有限公司,重庆 400707;3.重庆建设汽车系统股份有限公司 重庆市汽车热管理系统工程技术研究中心,重庆 400052)
旋叶式压缩机是一种新型回转式压缩机,具有部件少、转速高、效率高、成本低等优点,被广泛应用于中小排量汽车空调系统中[1-2]。在实际工作过程中,压缩机转子高速运转,叶片与转子槽、叶片与缸体接触冲击易诱发机体振动,引起外场辐射噪声,影响乘车舒适性;叶片与缸体、转子间的冲击摩擦、磨损磨耗也会影响压缩机寿命与压缩效率。因此,研究旋叶式压缩机动态接触激励对降低压缩机振动与噪声,提高压缩机寿命与压缩效率具有重要的工程应用价值。
在压缩机多刚柔耦合建模方面,彭斌等[3]建立了涡旋式压缩机小曲拐刚柔耦合模型,研究了曲拐节点应力应变变化规律;张春等[4]建立了涡旋式压缩机转子系统刚柔耦合模型,研究了小轴和动涡旋的应力应变分布;孙晓东等[5]建立了往复式压缩机轴系刚柔耦合动力学模型,研究了飞轮转动惯量对曲轴系统扭振特性的影响。在压缩机动态接触激励方面,黄华军等[6]建立了计及运动副间隙的涡旋压缩机动力学模型,研究了运动副间隙对压缩机转子系统的动平衡影响;Yang等[7]建立了双摆动式滑片压缩机(DSVC)动力学模型,分析了偏心轴承和轴轴承压力、叶片两侧与头部压力变化规律;He等[8]以摆浮式压缩机为研究对象,研究了摆浮式压缩机在不同排气压力下的机械效率和各部件之间的摩擦损失;Teh等[9]以单叶片回转压缩机为研究对象,建立了接触区域动载荷计算模型,研究了压缩机叶片和支撑轴承的摩擦损失;吴万荣等[10]以移动式双螺杆空气压缩机为研究对象,研究了用气量对空气压缩机系统压力的影响;Okur等[11]以新型铰链式回转压缩机为研究对象,分析了叶片厚度与质量对压缩机动力学特性的影响规律;Xiao等[12]建立了具有变化和汽缸下沉的单缸往复式压缩机的动态模型,研究了往复式压缩机的非线性动力学行为;Pont等[13]对往复式压缩机机构进行了动力学分析,研究了几何参数对二次运动稳定性、摩擦功率损失和压缩机消耗的影响;Chen等[14]针对旋叶式压缩机,研究了在不同冷媒情况下的叶片-滚子摩擦的摩擦因数和磨损深度。
综上所述,目前国内外研究者已对压缩机刚柔耦合建模与激励诱发机理开展了大量研究工作。然而,汽车空调旋叶式压缩机刚柔耦合动力学建模与叶片动态接触激励研究较少,且现有分析模型与方法并不完全适用于圆弧-简谐曲线组合型旋叶式压缩机叶片动态接触激励研究,比如实测基元腔压力如何耦合至柔性叶片、基元腔压力传递通道如何与叶片运动关联、背压腔压力如何考虑等力学边界问题。因此,本文基于刚柔耦合理论,建立旋叶式压缩机柔性叶片、刚性转子与腔体多刚柔耦合动力学模型,将实测基元腔压力、背压腔压力作为多刚柔耦合动力学模型力学边界,研究旋叶式压缩机多刚柔耦合动力学特性与叶片动态接触激励。
1 旋叶式压缩机刚柔耦合动力学建模
某汽车空调旋叶式压缩机由5个叶片、转子、缸体等部件组成,其中叶片头部为圆弧曲线,缸体内型线由简谐-圆弧曲线组成,为组合型线旋叶式压缩机,如图1所示。

1.气缸体;2.叶片头部;3.排气孔;4.转子槽;5.转子;6.转子槽分块部分;7.叶片尾端;8.简谐曲线;9.叶片;10.圆弧曲线
1.1 旋叶式压缩机刚柔耦合建模与约束关系确定
对于旋叶式压缩机来说,叶片相对于缸体、转子,其刚性较弱,故建模时将5个叶片处理为柔性,缸体与转子处理为刚性体,进而建立刚柔耦合动力学模型,能更准确地反应叶片与缸体、转子属于碰撞接触状态。借助六面体单元对5个叶片进行离散化处理,得到柔性化叶片模型,其中节点数为23 289。对柔性叶片进行网格质量检查,发现网格无任何警告与错误,网格离散质量合格。
借助三维建模软件UG,建立旋叶式压缩机缸体、转子、叶片刚性实体模型,装配得到三维多刚体模型。为便于后续提取叶片与转子槽两侧动态接触力,需在刚性实体建模阶段就对转子槽进行分块处理,转子槽分块部分见图1。而后,将旋叶式压缩机多刚体模型导入ADAMS软件中,并将刚性叶片复制,借助ADAMS/flex模块和叶片有限元网格模型,将复制的刚性叶片转化为柔性体,并定义原刚性叶片质量与惯性为零,使其变为“哑物体”,便于施加接触约束和提高多刚柔耦合数值计算效率。表1为各部件约束关系。
其中转子施加转动约束,如图2(a)中1所示;柔性体与“哑物体”、转子与转子槽分块部分、缸体相对于地面分别施加固定副,分别如图2(a)中2、3、6所示;“哑物体”端面与转子端面添加平面副,如图2(a)中5所示;“哑物体”与缸体、“哑物体”与转子槽分块部分分别施加Contact约束,如图3(a)中4所示,得到旋叶式压缩机多刚柔耦合动力学模型,如图3(b)所示。
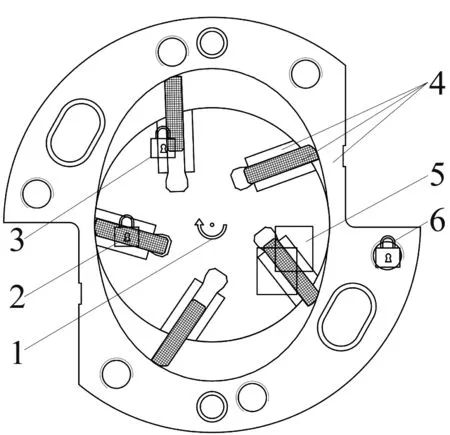
(a) 约束关系示意图

(a) 测试平台
1.2 叶片导入ADAMS前后模态对比
针对旋叶式压缩机叶片导入ADAMS前后做模态分析,结果如表2所示。相同质量作用力下,柔性体变形作用使得接触有效面积增大,有限元实际单元的接触力减小,在同等穿刺变形深度的约束下,接触刚度降低,因此柔性系统模态比刚性系统模态更小。
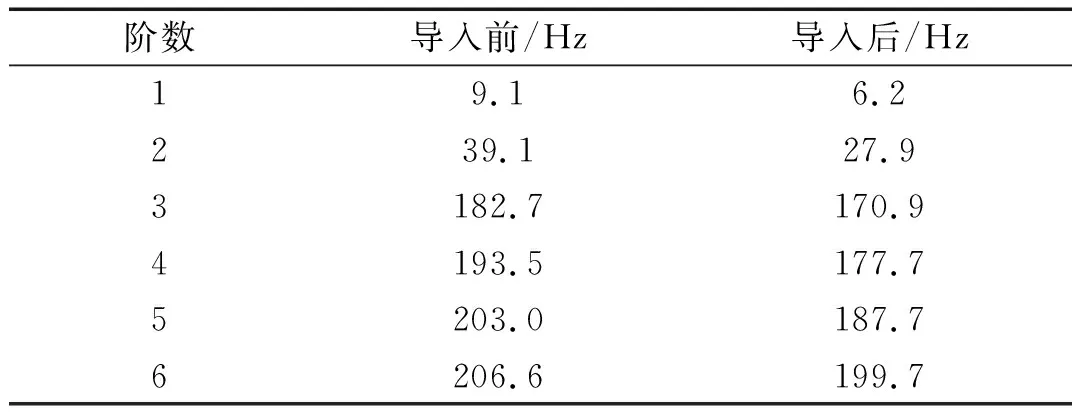
表2 模态频率
1.3 旋叶式压缩机多刚柔耦合力学边界条件
在旋叶式压缩机服役过程中,叶片尾端与左右两侧会分别受到来自背压腔的背压力与基元腔的气体力作用。课题组前期已通过基元腔气体压力测试与理论计算得到了此款旋叶式压缩机叶片所受气体作用力变化规律[15],如图3所示。
在添加背压腔的叶片背压力时,使其沿着转子槽方向,垂直作用于叶片尾端中心,且背压力恒定约为排气压力的0.75倍。在添加基元腔的气体力过程中,使其垂直作用于叶片伸出部分中心位置,且气体力随着基元腔容积变化而变化。
由于叶片随转子转动,叶片伸出长度随转子转角不断变化,气体力作用点也将随之改变。因此,需构建一质量与体积近乎为零的“无质量块”作为基元腔气体力的受力载体,并对“无质量块”与“哑物体”施加滑动副约束,且施加平移驱动,使“无质量块”始终与叶片伸出部分中心位置重合。
提取叶片伸出转子槽长度结果的1/2,将其作为“无质量块”的位移数据,将其转化为样条曲线;进而,基于样条曲线对平移驱动编写“无质量块”位移加载函数,使“无质量块”与叶片相对滑动,保持在叶片伸出部分的中心位置;而后,将实测基元腔的气体力施加到“无质量块”上,实现将基元腔的气体力传递至叶片的目的。叶片加载模型,如图4所示。

图4 叶片加载模型
2 旋叶式压缩机叶片运动学特性
2.1 旋叶式压缩机刚柔耦合模型验证
为验证旋叶式压缩机刚柔耦合计算值的正确性,与运动学解析值进行对比分析,保证建模及约束关系的合理性。
旋叶式压缩机叶片运动特性曲线是叶片沿槽方向位移、速度与转子转角的关系表达式。首先,设缸体型线极坐标方程为ρ=ρ(θ)构成的气缸型线T,叶片圆弧圆心的运动轨迹为Tv,以Tv上的任意点为圆心,以R0为半径作一系列小圆,其外包络线为T,即基于等距曲线包络原理,建立旋叶式压缩机数学模型如图5所示,其中缸体型线为已知量,其上每点曲率半径表示为ρ。
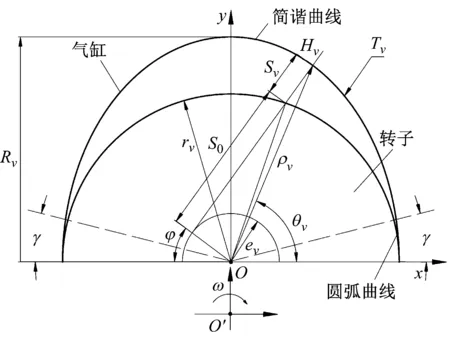
图5 旋叶式压缩机数学模型
针对该多段圆弧-简谐曲线组合型旋叶式压缩机的气缸型线方程可表示为
(1) 当-γ<θ<γ、180°-γ<θ<180°+γ时,气缸型线方程为
ρ=r
(1)
叶片沿槽方向的位移为
S=0
(2)
转子转角极坐标极角关系式为
(3)
(2) 当γ<θ<180°-γ时,气缸型线方程为
ρ=r+(R-r)sin2[λ(θ-ξ1)]
(4)
叶片沿槽方向的位移为
(5)
转子转角极坐标极角关系式为

(6)
(3) 当180°+γ<θ<360°-γ时,气缸型线为
ρ=r+(R-r)sin2[λ(θ-ξ2)]
(7)
叶片沿槽方向的位移为
(8)
转子转角极坐标极角关系式为
(9)

表3为压缩机部分参数规格。将表3数据代入式(1)~(9)中得到叶片运动特性解析值。

表3 压缩机部分参数
求解压缩机刚柔耦合模型,在ADAMS软件中测得叶片运动特性仿真值,并与上述解析值对比结果如图6所示。分析可知,叶片位移、速度运动特性曲线解析解与仿真值规律吻合较为良好,验证了旋叶式压缩机刚柔耦合建模与约束关系的合理性。

(a) 叶片位移曲线对比
2.2 旋叶式压缩机叶片动态接触激励计算
旋叶式压缩机运行过程中,叶片随转子一起转动,在离心力与背压力作用下在叶片槽内来回平动,叶片受到与缸体的动态接触力Fm、与转子槽两侧的动态支反力R1、R2及背压腔压力Fb作用,其中背压腔压力为0.7倍~0.8倍排气压力Pd,叶片受力示意图如图7所示。

图7 叶片受力示意图
基于旋叶式压缩机刚柔耦合动力学模型,其接触参数如表4所示,设置求解时间0.2 s,时间步长1×10-4s,计算得到转子转动一圈过程中叶片与缸体动态接触力、叶片与转子槽动态接触力。图8给出了压缩机在背压力为0.75Pd,转速3 000 r/min工况下叶片动态激励。

表4 接触参数

(a) 叶片与缸体
分析可知,叶片与缸体间动态接触力存在剧烈波动,最大值为453 N,均值为250 N,出现在进气、压缩气体两个过程交界处;R2波动较R1剧烈,进气与压缩转化过程中,叶片-缸体间动态接触力与背压力达到平衡状态;随着基元腔容积变小不断压缩介质,R1与R2均急剧增加,当基元腔气体作用力最大时,支反力达到峰值。
刚柔耦合计算值较全刚体模型相比,叶片与缸体间接触力Fm数值上存在一定偏差,相差35.20%,叶片转子槽两侧的动态支反力R1、R2数值分别相差14.97%、2.94%。因此,进行刚柔耦合处理能更准确的反应叶片与缸体、转子的碰撞接触状态。
3 叶片动态接触激励影响因素分析
3.1 转子转速
图9给出了背压力为0.75Pd,动摩擦因数为0.08下,旋叶式压缩机叶片动态接触力均值随转速变化规律。

图9 不同转速下叶片接触力均值
分析可知,转速3 000 r/min以下,R1与R2变化较为平缓,但随着转速增加,R1与R2则变化较为激烈;转速4 800 r/min以下,Fm随着转速增大而增大,当转速大于6 000 r/min,Fm小于Fb,叶片则会出现“脱空”现象,导致泄露;压缩机在不同转速工作时,应合理控制背压腔压力变化,不能为恒定值。
3.2 背压腔背压
图10给出了转速为3 000 r/min,动摩擦因数为0.08下,旋叶式压缩机叶片动态接触力均值随背压变化规律。

图10 不同背压下叶片动态接触力均值
分析可知,随着压缩机启动运转,R1、R2、Fm随背压力增大而增大,均呈近似线性增加;背压力增加可以保证叶片与缸体不“脱空”,但背压值过大将引起较大的摩擦损耗,同样也验证了压缩机在设计阶段应该合理控制背压腔压力变化的结论。
3.3 叶片结构参数
原旋叶式压缩机叶片头部型线为单段圆弧,通过对叶片左右两侧圆弧进行修正,调整为三段圆弧,如图11所示。

(a) 原叶片
为验证结构化网格的合理性,分别取节点数为27 578,34 750与41 802的三种网格模型。图12给出了三种网格模型的叶片头部节点应力变化规律,网格模型1的叶片应力精度相对不高,网格模型2、3精度相似。因此,为了节约计算资源,选用节点数为34 750的网格模型2进行数值模拟。

图12 三份网格模型叶片与缸体接触应力
基于上述刚柔耦合建模与约束方法,建立含新叶片的压缩机刚柔耦合动力学模型,求得背压力为0.75Pd,转速为3 000 r/min下,压缩机叶片与缸体动态接触力最大值与均值分别为407 N、251 N;对比2.2节原叶片与缸体动态接触力计算结果,两者数值相差约10%、0.4%,两者相差较小;但原叶片、新叶片与缸体接触应力应变差别较大,如图13所示。

图13 叶片与缸体接触应力
分析可知,新叶片的应力较原叶片小,且叶片两侧应力降低显著,最大的减小量约为80%;将叶片由单圆弧改为三圆弧后,虽接触力最大值、均值与原结构差别不大,但应力值大大降低,有助于改善叶片与缸体冲击接触状态与提高叶片抗疲劳强度能力。
4 结 论
针对圆弧-简谐曲线组合型旋叶式压缩机,建立了压缩机柔性叶片、刚性转子与腔体多刚柔耦合动力学模型,将基元腔压力测试数据以无质量块形式传递至柔性叶片、背压腔压力施加于叶片背部作为力学边界条件,研究旋叶式压缩机叶片与缸体、转子间的动态接触激励。主要结论如下:
(1) 叶片运动位移、速度解析值与仿真值规律吻合较为良好,验证了旋叶式压缩机刚柔耦合建模与约束关系的合理性。
(2) 在进气与压缩气体过程交界处,叶片与缸体动态接触力达到最大值,背压力同叶片与缸体间动态接触力达到平衡状态,且基元腔作用力最大时,支反力达到峰值;为降低摩擦损耗,应对压缩机背压腔压力进行动态控制。
(3) 将压缩机叶片单段圆弧修正为三段圆弧后,有助于改善叶片与缸体冲击接触状态与提高叶片抗疲劳强度能力。

