衬套型橡胶悬置结构形状的优化方法
郭一鸣, 吴钟恺, 上官文斌
(1.湖北汽车工业学院 汽车动力传动与电子控制湖北省重点实验室,湖北 十堰 442002;2.华南理工大学 机械与汽车工程学院,广州 510641)
橡胶悬置作为一种弹性元件使动力总成与车架相连,起到支撑、限位、隔振等作用[1]。悬置系统的设计和整车NVH性能之间有着密切的关系,动力总成的振动沿着传递路径首先通过悬置系统,再通过一系列的连接件传递到车身,造成车身振动使车内噪声加大。合理匹配动力总成悬置系统,则可以满足刚体振动模态的固有频率和实现系统振动解耦的目标,以降低车内振动及噪声。实现方法通常采用改变安装位置,安装角度以及刚度等悬置系统参数。受动力总成布置形式限制,安装位置及安装角度往往难以改变,因此,改变悬置刚度以匹配动力总成悬置系统成为最合理的方法。橡胶悬置的刚度参数不仅与材料特性相关, 也与结构有关。国内外已对悬置刚度性能做了一系列研究[2-4]。研究人员也对结构参数方面进行了研究。Kim等[5]提出了参数化设计方法,结合有限元软件,对某发动机悬置进行分析,优化得到最终模型。Lee等[6]提出了橡胶隔振器拓扑优化设计方法采用密度分布法同时考虑静态和动态性能。Kaya等[7]使用微分进化算法对形状优化以确定橡胶衬套的模型参数。赵建才等[8-9]通过神经网络和遗传算法结合的策略对悬置几何参数进行优化。丁智平等[10]通过研究锥形橡胶弹簧结构参数对刚度和最大主应变范围的影响,对锥形弹簧结构参数进行优化,优化结果较好。
研究人员大量针对橡胶填充结构进行优化分析,很少针对非橡胶填充结构进行分析。因此本文针对某汽车动力总成悬置,对其非橡胶填充结构进行研究。采用正交试验与有限元结合的方法,将非橡胶填充的结构参数与其静刚度的关系建立二阶响应面模型,采用谢菲尔德遗传算法实现多目标优化从而获取最优的结构参数以满足设计目标,优化结果误差较小满足设计要求。
1 非橡胶填充结构对橡胶悬置刚度的影响分析
由于在匹配动力总成悬置系统时橡胶悬置在各方向上的刚度值均不同,且在不同频率和变形条件下的刚度值也不同,因此设计悬置时,各方向的刚度设计尤为重要。本文选取衬套型橡胶悬置作为研究对象,该结构中橡胶可承受压力或剪切力,或两者兼有之[11]。衬套型悬置的耐久性能好,静刚度曲线线性段较小,结构紧凑,适合布置空间较小的车辆使用。
该悬置主要由内管,外套和橡胶部分组成,内管和外套均为金属与橡胶粘接硫化而成,非橡胶填充结构对称布置,结构如图1所示。U向为整车x向,V向为整车Y向,W向为整车z向。W向主簧之间夹角呈180°,此时W向具有较大刚度,可以使悬置在常用载荷工况下,主要承受压缩载荷,以提高结构的疲劳耐久性能。U向主簧上设有非橡胶填充结构,使得汽车在加减速工况下具有良好的缓冲作用。V向承受剪切作用,刚度较低,非橡胶填充结构使V向刚度进一步降低,因此悬置与支架间往往有硬限位设计,在动力总成承受较大的侧向力时限制其位移行程,保证金属骨架与橡胶之间不拉脱,橡胶主簧不拉断。

图1 橡胶悬置结构
运用ABAQUS软件建立如图2所示的有限元模型,网格采用C3D8H六面体单元。根据实际工况对模型进行约束,约束外圈表面的6个自由度,将内圈表面绑定在形心处,在形心处施加-5 mm位移载荷,提取形心处-1~-4 mm的反作用力与位移曲线即刚度曲线。橡胶本构模型选用M-R模型,描述不可完全压缩超弹性材料的性能[12],模型参数为C10=0.301,C01=0.065[13]。

图2 橡胶部分有限元模型
2 橡胶悬置非橡胶填充结构参数分析
选取对非橡胶填充结构影响较大的尺寸作为设计变量。悬置截面关于原点对称,选取1/4结构进行参数化设计。非橡胶填充结构各参数为α,β,r,R,具体如图3所示。r为长槽的半径,R为圆槽的半径,α为两槽间的夹角,β为长槽的角度。

图3 橡胶悬置结构参数设计
文中在进行非橡胶填充结构优化设计时, 忽略噪声因素的影响, 只需考虑内外表的内表 (即正交表) 的设计[14],根据选取的设计参数(4个)与水平数(4个),见表1。正交表选用L16(45),其中1,2,3,4列为4个设计参数的不同水品,第5列为空白列,在ABAQUS中逐一进行模拟分析,并将试验结果记录在表2中。

表1 各因素的水平列表
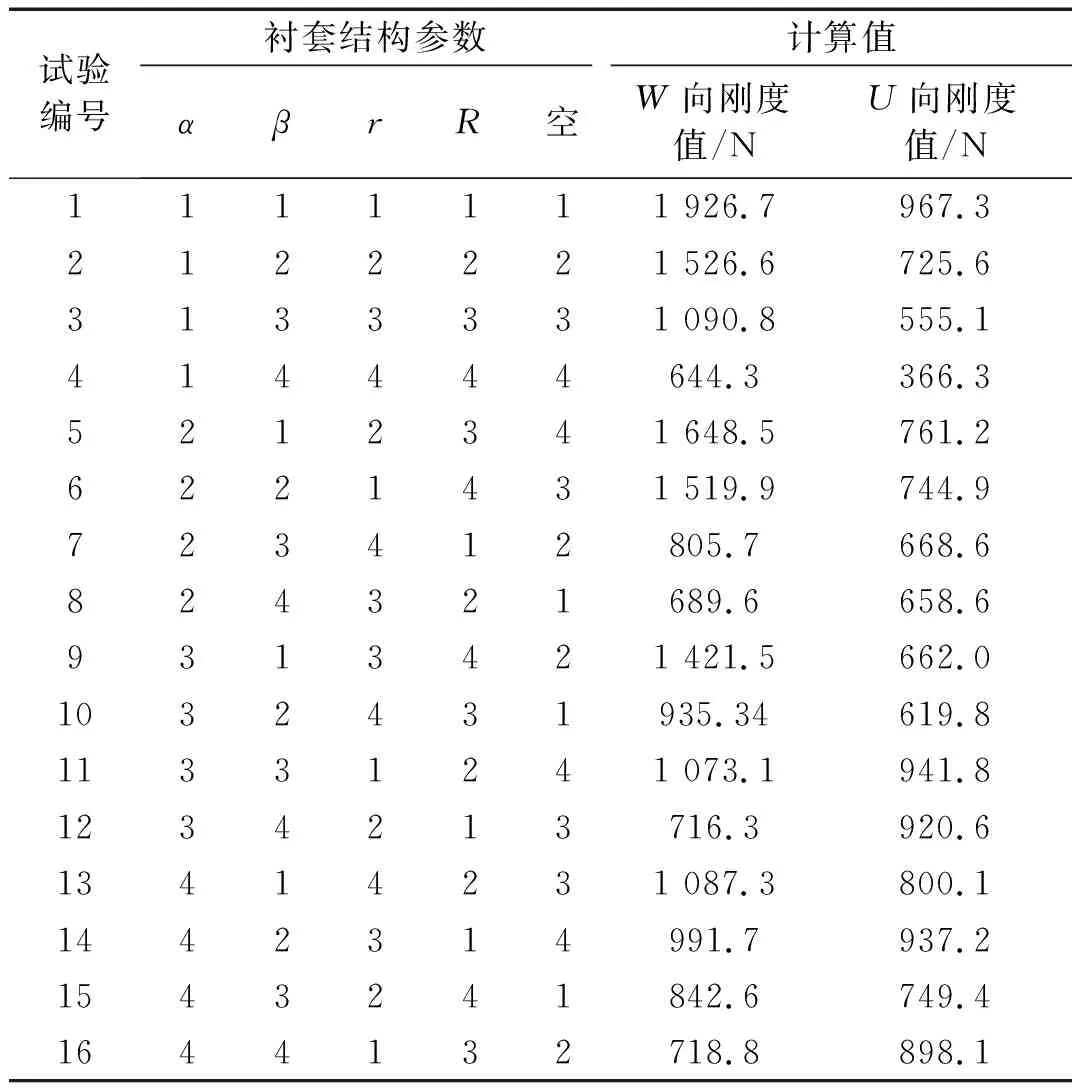
表2 4因素4水平正交试验结果
根据表2中有限元计算得到的计算值,计算得到W向与U向刚度计算值的响应值表见表3和表4。在正交试验设计中,一般采用极差分析法来评定试验因素重要性顺序,极差越大,说明该参数对试验结果影响越大[15]。
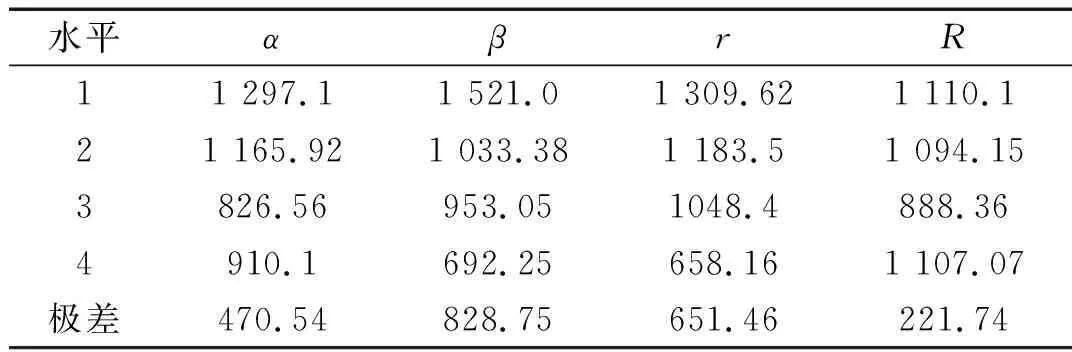
表3 W向刚度值响应值

表4 U向刚度值响应值
根据极差分析可知,各因素对W向刚度影响大小的顺序为:长槽的角度β>长槽半径r>两槽间夹角α>圆槽半径R,可知对W向刚度影响最大的因素是长槽的角度β,因此在调整W向刚度时可以通过改变长槽的角度β来实现。
各因素对U向刚度影响大小的顺序为:长槽半径r>圆槽半径R>两槽间夹角α>长槽的角度β,可知对U向刚度影响最大的因素是长槽半径r,因此在调整U向刚度时可以通过改变长槽半径r来实现。
3 橡胶悬置刚度的响应面模型
3.1 响应面模型构建
当响应变量和自变量之间呈现非线性时,需采用高阶多项式拟合。若采用三阶或更高阶多项式拟合时,可能会产生龙格现象,且随着变量个数增加,计算成本会成倍增加。工程实际中,多采用二阶响应面模型。二阶响应面的函数表达式为
i,j=1,2,……,n
(1)
式中:n为自变量总数xi、xj为自变量;a为多项式系数;ε为误差项。
将式(1)转化为多元线性回归方程,对于多个设计变量的线性回归模型为
Y=β0+β1x1+…+βnxn+ε
(2)
将式(2)写为矩阵形式,令
则多元线性回归模型可表示为
Y=Xβ+ε
(3)
未知系数向量β采用最小二乘法[16]
(4)
将表2中长槽的半径r,圆槽的半径R,两槽间的夹角α,长槽的角度β作为设计变量,U向刚度值KU,W向刚度值KW为目标值,构建二阶响应面模型为
(5)
式中:KW为W向刚度值;KU为U向刚度值;ZW、ZU为系数向量,其形式分别如式(6)、(7)所示;u为基函数向量,其形式如式(8)所示。系数向量计算结果见表5。
ZW=[ZW1,ZW2,ZW3,…,ZW14]
(6)

表5 系数向量计算结果
ZU=[ZU1,ZU2,ZU3,…,ZU14]
(7)
u=[1,α,α2,β,β2,r,r2,R,R2,αβ,αr,αR,βr,βR]
(8)
3.2 误差分析
为检测响应面模型的误差,本文采用R2分析,表达式为
(9)
其中
SSr=SSR+SSE
(10)
式中:SSR为回归平方和;SSE为残差平方和。
本文随机选取10个点作为误差分析点,以U方向为例,从表6可以看出U向响应面模型的R2大于0.9,该二阶响应面模型具有较高的可信度。

表6 R2分析
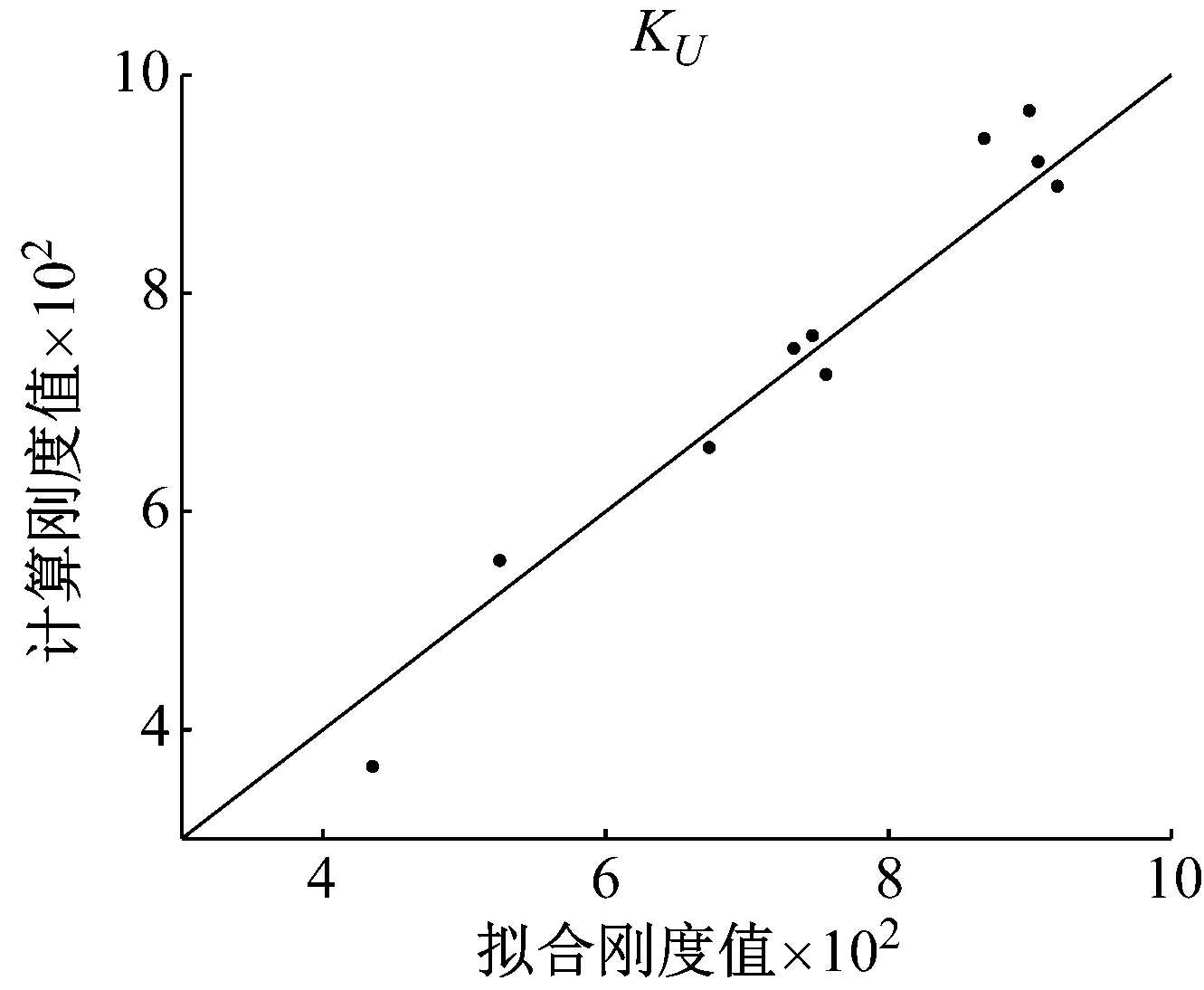
图4 U向误差分析
4 橡胶悬置非橡胶填充结构参数优化
动力总成悬置系统匹配过程中,振动耦合度和固有频率的合理分配是评价整个系统隔振的重要指标。悬置参数设计极为重要,在同一生产线上匹配不同动力总成时,往往悬置安装位置及悬置安装角度都难以改变,因此通过改变悬置刚度以匹配悬置系统的固有频率,降低振动耦合度,成为最合理的方法。通过已建立的响应面模型,以刚度值为设计目标,非橡胶填充结构参数为设计变量,进行优化设计。
4.1 多目标遗传算法优化方法
在优化设计过程中,以长槽的半径r,圆槽的半径R,两槽间的夹角α,长槽的角度β作为设计变量U向刚度值KU,W向刚度值KW为目标,且满足望目特性。KU目标值以750 N/mm为例,KW目标值以1 000 N/mm为例。建立数学模型如下
minF1=|KW-1 000|
minF2=|KU-750|
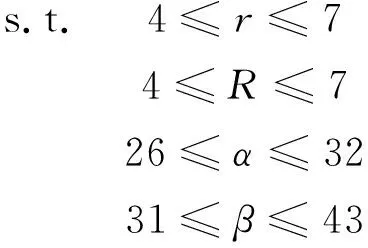
(11)
利用构建的二阶响应面模型进行优化计算。本文采用MATLAB中谢菲尔德遗传算法工具箱对橡胶悬置刚度进行优化,采用并列选择法进行多目标优化匹配。对设计变量进行10位二进制编码,种群数目为500,最大遗传代数为100,代沟为0.9。经过200次遗传迭代后,结果如图5~图6所示。经过200次迭代计算后,最终得到目标函数的解,从而可计算得到目标刚度值,相对应的优化变量的值为:长槽的半径r=5.17 mm,圆槽的半径R=6.67 mm,两槽间的夹角α=28.02°,长槽的角度β=39.37°,将计算结果取整得到最终结果为长槽的半径r=5 mm,圆槽的半径R=7 mm,两槽间的夹角α=28°,长槽的角度β=39°。

图5 200次迭代后F1的最优解及性能跟踪

图6 200次迭代后F1与F2的值
4.2 优化结果验证
根据优化结果得到的最佳参数加工成样品,试验采用MTS831.50弹性体试验系统,试验时,垂向加载6 mm,加载速度为2 mm/min,取值区间为2~4 mm,预循环1次,取第2次加载过程的力-位移曲线。目标值,拟合值与试验值结果对比,如表6所示。

表6 优化结果与试验结果对比
分析表6中的数据可知:根据优化结果对橡胶悬置结构参数取整后,代入二阶响应面模型计算,拟合结果为U向刚度值为783 N/mm,W向刚度值为1 014.7 N/mm;试验所得的结果U向刚度值为847 N/mm,W向刚度值为1 130 N/mm。两个方向的刚度值误差分别为8.1%和11.3%。产生该误差的主要原因是在选取本构模型参数时,对应的橡胶硬度为55 HA,而实际硬度为57 HA。橡胶在密炼、混炼以及硫化过程中,其硬度存在误差,橡胶硬度存在±2 HA的公差范围内都是正常,导致试验结果比拟合结果大。根据经验,橡胶硬度范围在±3 HA波动时,刚度值误差为±15%。因此误差在15%以内时,认为该仿真精度达到要求。
5 结 论
(1) 利用正交试验的方法,采用极差分析法得到各参数对不同方向刚度值的响应程度,W向刚度影响大小的顺序为:长槽的角度β>长槽半径r>两槽间夹角α>圆槽半径R;U向刚度影响大小的顺序为:长槽半径r>圆槽半径R>两槽间夹角α>长槽的角度β。
(2) 通过建立二阶响应面模型,获得非橡胶填充结构参数与刚度值之间的关系。
(3) 利用二阶响应面模型和谢菲尔德遗传算法工具箱对非橡胶填充结构参数进行优化,并对优化结果进行试验验证,两个方向刚度值的误差分别为8.1%和11.3%,均小于15%,误差较小。

