桁架加劲梁悬索桥后颤振特性节段模型试验研究

张瑞林， 杨鸿波， 刘志文， 杨 健， 陈政清

(1.湖南大学 风工程与桥梁工程湖南省重点实验室,长沙 410082；2.湖南大学 土木工程学院，长沙 410082；3.贵州省交通规划勘察设计研究院股份有限公司，贵阳 550081)

颤振作为一种典型的风致振动现象，会引起桥梁主梁大幅振动，甚至引起桥梁垮塌，因此颤振稳定性是大跨度桥梁设计中必须进行检验的重要指标之一。目前，Scanlan线性颤振分析理论[1]广泛用于大跨度桥梁颤振研究中，其主要目标用于评价颤振临界风速，根据该理论可知，当风速大于颤振临界风速后桥梁主梁结构位移响应会无限增大。然而，实际桥梁主梁颤振现象往往并非如此，如1940年，旧塔科马桥在风毁之前曾发生最大扭转振幅达35°，且持续时间近70 min的振动，最终因吊杆断裂而引起垮塌[2]。

已有风洞试验与计算流体动力学(computational fluid dynamics，CFD)数值模拟研究表明，部分桥梁主梁断面在后颤振状态具有复杂的非线性特征，而不是线性发散状态。比较典型的非线性颤振表现为极限环振动特征，即风速大于颤振临界风速时出现自限幅振动，其位移相平面的轨迹线构成闭合的环形，故称其为极限环振动(limit cycle oscillation,LCO)，且振幅随风速增大而持续增大。一些学者将其称为“软颤振”，以区别发散型的“硬颤振”。Amandolese等[3]进行了两自由度平板颤振试验研究，结果表明平板颤振表现为极限环振动，并指出气动力非线性的重要性。朱乐东等[4]对全封闭箱梁、中央开槽箱梁、半封闭箱梁与双边肋等四种典型断面进行了试验研究，结果表明上述四种断面均可能出现不同程度的软颤振现象。Zhang等[5]、Gao等[6]分别进行箱梁与双边肋梁后颤振试验研究，结果均表明箱梁与双边肋梁极限环振动弯扭耦合效应较弱，可视为扭转颤振。Ying等[7]采用CFD数值模拟的方法研究了不同风攻角下箱梁断面的颤振性能，结果表明，箱梁断面在0°与+3°风攻角下表现为发散性颤振，±5°风攻角下表现为极限环振动。Tang等[8]通过节段模型试验研究了Π型断面主梁后颤振性能，结果表明Π型断面主梁后颤振表现为极限环振动，并且风攻角对颤振临界风速与极限环振动稳定振幅均有显著影响。伍波等[9]研究了双层桥面桁架梁软颤振性能，并分析了初始激励与扭弯频率比对软颤振的影响。结果表明，双层桥面桁架梁软颤振具有振幅唯一性，不同激励对应同一振幅，扭弯频率比越大，软颤振振幅越小。

实际桥梁结构非线性颤振产生原因主要包括气动力非线性、结构阻尼非线性与刚度非线性。气动力具有复杂的非线性特征，朱乐东等[10-11]建立了非线性气动力模型，用来描述非线性气动力以及解释极限环振动现象。此外，已有研究表明[12]，广泛用于桥梁颤振研究的弹性悬挂节段模型试验系统存在阻尼与刚度非线性。Wu等[13]在极限环振动振幅计算中考虑了节段模型阻尼非线性。Zhang等[14-15]的数值模拟研究结果表明，结构几何非线性可以引起极限环振动。

综合学者以往对桥梁后颤振的研究成果可以发现，目前对桁架梁后颤振特性的研究相对较少。此外，多数后颤振研究主要考虑气动力非线性，而对弹性悬挂节段模型试验系统结构非线性因素考虑较少。为此，本文以某大跨度桁架加劲梁悬索桥为工程依托，采用弹性悬挂节段模型试验方法，对桁架梁后颤振极限环振动特征与机理进行研究。

1 工程概况与试验装置

1.1 工程概况

以开州湖大桥为工程依托，该桥位于贵州省开阳县境内。主桥为主跨L=1 100 m单跨简支钢桁架加劲梁悬索桥，主缆垂跨比为f/L=1/10，加劲梁宽为27.0 m，桁高为7.2 m。主桥总体布置立面图与桁架加劲梁标准断面图,如图1所示。主桥结构成桥状态一阶对称竖弯频率与一阶对称扭转频率分别为0.158 6 Hz和0.313 6 Hz，对应的等效质量与等效质量惯性矩分别为28.50 T/m与3 370.0 T·m2/m。主要模态结果如图2所示。

(a) 主桥总体布置立面图

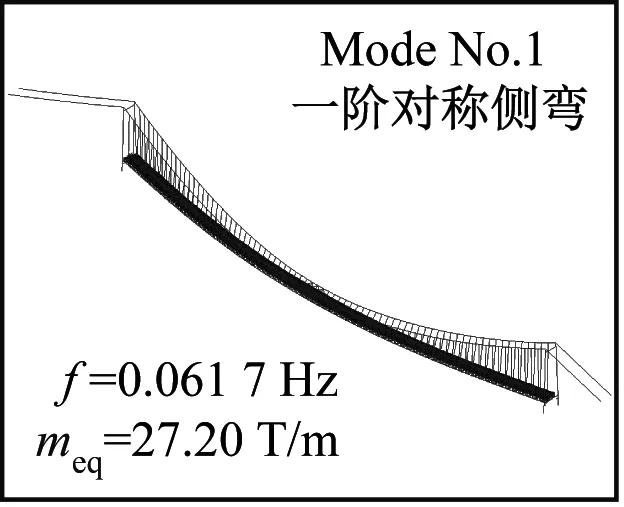
图2 开州湖大桥主桥结构主要模态

1.2 试验装置

桁架加劲梁节段模型风洞试验在长沙理工大学边界层风洞实验室高速试验段中进行，该试验段尺寸为宽4.0 m、高3.0 m、长17 m，最大试验风速为45.0 m/s，且连续可调。

综合考虑，确定桁架梁节段模型几何缩尺比λL=1∶50，模型长度L=1 728 mm，宽度B=540 mm，高度H=144 mm。模型骨架采用钢板与钢管框架制作，桥面系与桁架杆件采用ABS板制作，以保证几何外形相似。

采用弹性悬挂节段模型试验系统进行桁架梁颤振测试，风攻角为0°、±3°与±5°，试验均在均匀流场下进行。桁架梁节段模型通过两侧端杆连接8根弹簧，可以作竖向与扭转振动，侧向位移通过两根轻质水平钢丝给予约束。置于风洞中的弹性悬挂桁架梁节段模型,如图3所示。

图3 弹性悬挂桁架梁节段模型

2 非线性结构动力参数识别

2.1 识别方法

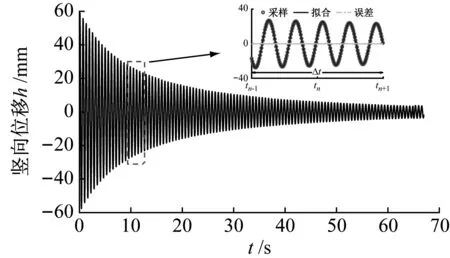
在无风环境下分别对桁架梁节段模型施加竖向与扭转初始激励，使其作自由振动，通过模型系统的自由振动衰减时程曲线识别该系统的瞬时频率与阻尼比。桁架梁节段模型竖弯与扭转自由振动衰减曲线，如图4所示。

(a) 竖向

采用分段最小二乘拟合方法识别弹性悬挂桁架梁节段模型试验系统的瞬时频率与瞬时阻尼比，具体步骤为：①截取时间中心为tn，长度为Δt的信号，根据式(1)进行最小二乘拟合，即可得到tn时刻对应的频率、阻尼比，根据式(2)得到tn时刻对应的振幅；②之后采用同样的方法在tn+1时刻进行拟合。部分拟合结果见图4(a)。

q(t)=q0e-ξωtsin(ωt+φ0)

(1)

qamp(tn)=q0e-ξωtn

(2)

式中:q(t)为竖向或扭转的位移信号；ξ为阻尼比；ω为圆频率；q0与φ0分别为初始振幅与初始相位的未知参数；qamp(tn)为tn时刻对应振幅。

2.2 识别结果

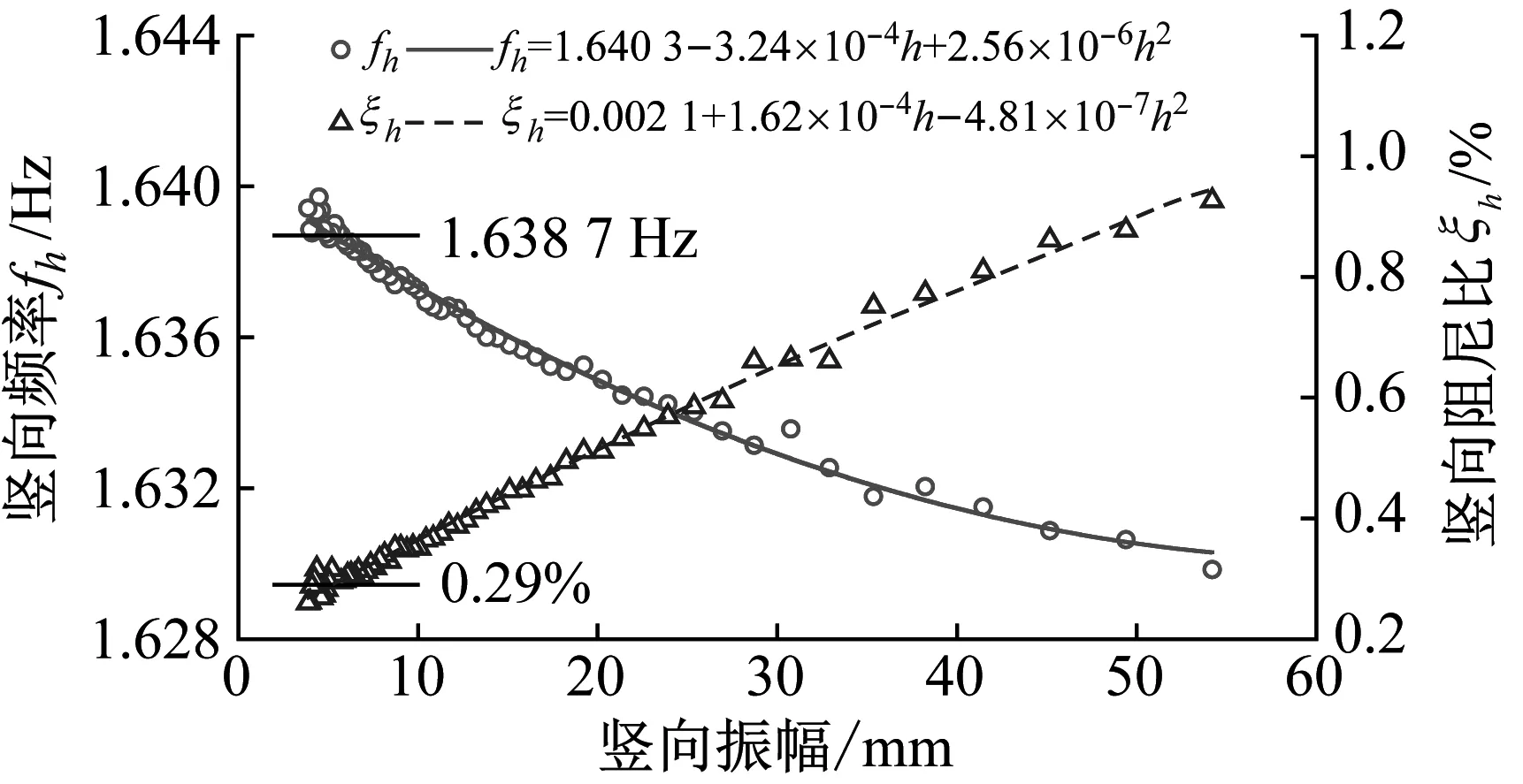
桁架梁节段模型的频率与阻尼比识别结果，如图5所示。并用二次多项式拟合，将桁架梁节段模型的频率、阻尼比表示为振幅的函数。

(a) 竖向

由图5可知，桁架梁节段模型的竖向与扭转频率均随振幅增大而轻微减小，而竖向与扭转阻尼比均随振幅增大而显著增大，即在弹性悬挂桁架梁节段模型试验系统中，存在较为轻微的刚度非线性与明显的阻尼非线性。

为直观表现以及便于后续分析，采用小振幅下(扭转振幅α0=1°、竖向振幅h0=5 mm)的频率、阻尼比作为弹性悬挂桁架梁节段模型试验系统的基本动力参数，如表1所示。

表1 桁架梁节段模型动力特性参数

3 后颤振响应特征

3.1 静位移

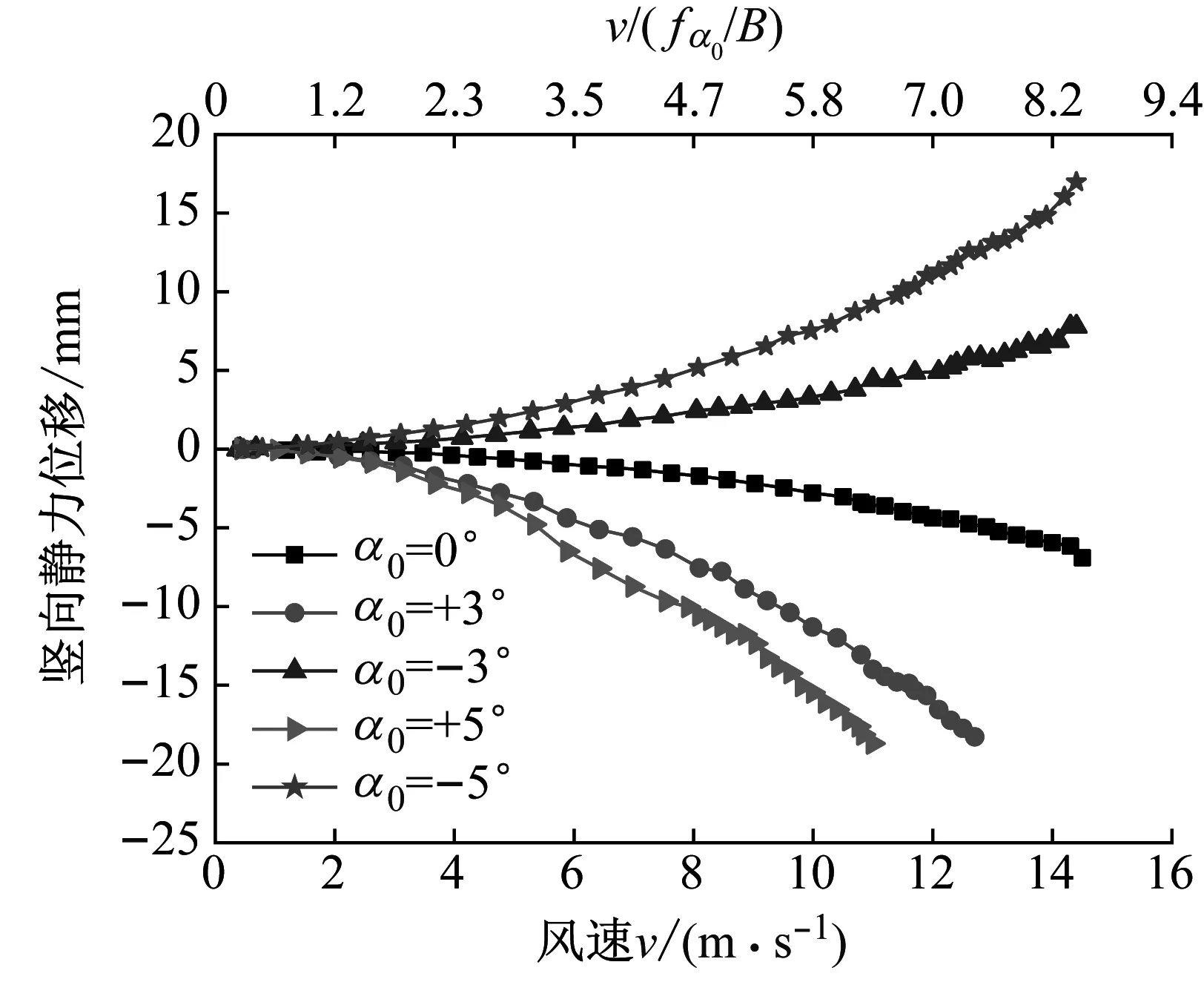
在均匀流场中，桁架梁节段模型位移响应主要由两部分组成，分别为气动自激力引起的振动位移与平均风荷载引起的静位移。静位移会引起附加风攻角，改变桁架梁节段模型的初始风攻角，可能会对颤振临界风速产生一定影响[16]。对桁架梁节段模型位移时程取平均,分别得到竖向与扭转静位移，结果如图6所示，其中竖向位移方向向下为正，扭转位移方向顺时针为正。

(a) 竖向

由图6(a)可知，桁架梁节段模型竖向静位移随风速增大而增大。在0°风攻角下，桁架梁节段模型竖向静位移总体较小。

由图6(b)可知，在+3°与+5°风攻角下，桁架梁节段模型扭转静位移随风速变化相对杂乱，数值总体较小，颤振临界状态对应的静力扭转位移不超过0.1°，表明在+3°与+5°风攻角下，桁架梁节段模型气动力矩系数较小，即在+3°与+5°风攻角下，静力扭转位移对桁架梁节段模型颤振性能影响较小；在0°，-3°与-5°风攻角下，桁架梁扭转静位移随风速增大而增大，其中，-5°风攻角颤振临界状态对应的静力扭转位移约为-0.8°，可能会对颤振临界风速产生一定影响。

3.2 颤振临界风速与稳态振幅

在0°、±3°与±5°风攻角下，桁架梁节段模型竖向与扭转振幅随风速的变化如图7所示。由图7可知，桁架梁节段模型振幅随风速增加而持续增加，并未出现发散性振动，即桁架梁节段模型后颤振现象表现为极限环振动。

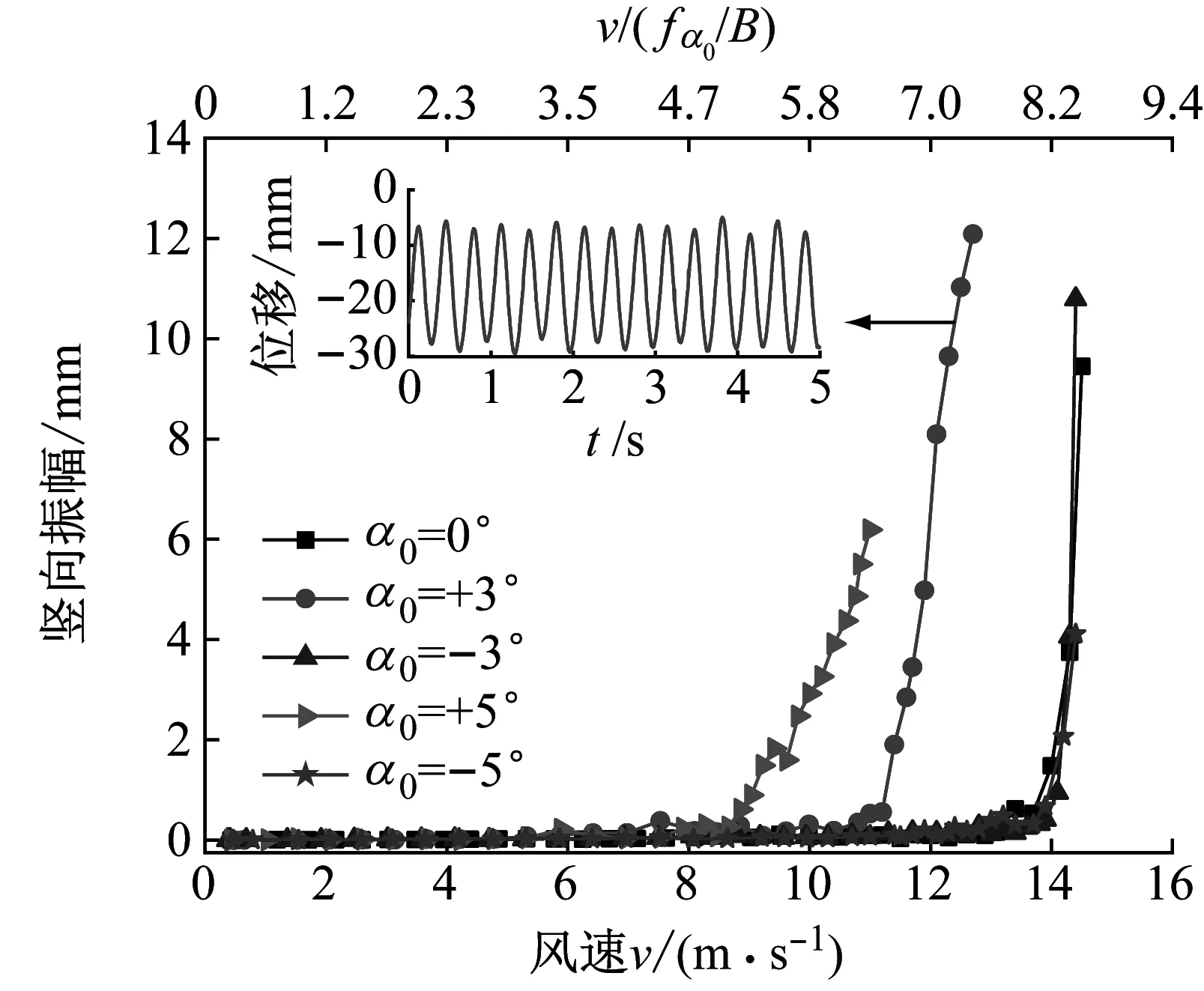
(a) 竖向

由图7可知，风攻角对桁架梁节段模型颤振临界风速有较大影响，当以扭转位移标准差为0.5°作为颤振临界风速的判定界限时[17]，在0°、-3°与-5°风攻角下桁架梁节段模型颤振临界风速较高，三者较为接近，分别为13.7 m/s、14.1 m/s与13.9 m/s。在正风攻角下，桁架梁节段模型颤振临界风速显著下降，+3°与+5°风攻角下颤振临界风速分别为11.2 m/s与8.86 m/s。

风攻角对桁架梁节段模型极限环振动振幅随风速增长的斜率也有较大影响，在 0°、-3°与-5°风攻角下，桁架梁节段模型极限环振动稳态振幅增长较为剧烈(曲线斜率较大)，接近于“硬颤振”。 在+3°与+5°风攻角下，桁架梁节段模型极限环振动稳态振幅增长相对缓慢。在颤振临界风速最低的+5°风攻角下，桁架梁节段模型极限环振动的振幅增长最为缓慢(曲线斜率较小)。

上述现象主要原因为在正风攻角下桁架梁节段模型气动外形更为“钝”化，导致颤振临界风速明显下降，极限环振动稳态振幅增长缓慢。同时应当指出，不同风攻角下桁架梁后颤振现象与Ying等的箱梁断面相比存在一定差异，该箱梁断面在±5°风攻角下表现为极限环振动，而在0°与+3°风攻角下表现为发散性颤振。说明对于不同类型断面，风攻角对后颤振性能的影响可能是不同的。

3.3 位移时程与频谱特性

为详细说明桁架梁节段模型后颤振位移响应特征，以+3°风攻角为例，选取三种振动状态，风速分别11.2 m/s、11.6 m/s与12.7 m/s。根据桁架梁节段模型位移时程，通过快速傅里叶变换得到时程响应的频谱特性，桁架梁节段模型位移时程与幅值频谱结果如图8所示。

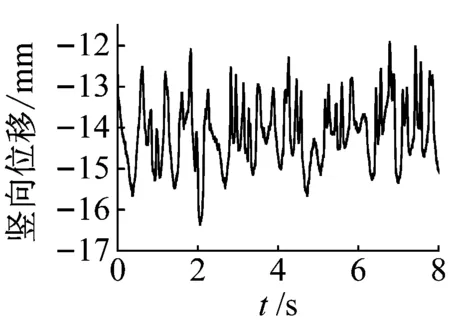
(a) v=11.2 m/s

由图8(a)可知，当风速为11.2 m/s时，桁架梁节段模型扭转位移相对较为规则，主要为单频成分，振幅为0.48°。桁架梁节段模型竖向位移包括两个卓越频率成分，与扭转运动同频的成分大于竖向基频附近的成分，表明该状态下具有一定程度的弯扭耦合。

由图8(b)可知，当风速为11.6 m/s时，桁架梁节段模型扭转位移接近简谐运动，振幅为2.4°。桁架梁节段模型竖向位移主要为与扭转运动同频的成分，也包括较小竖向基频附近的成分，可以认为该状态下扭转与竖向位移完全耦合。此外，竖向位移出现一定倍频成分，频率约为主频的2倍，这是由于桁架梁节段模型大幅振动下气动力存在倍频成分，进而产生倍频位移。

由图8(c)可知，当风速为12.7 m/s时，桁架梁节段模型扭转位移几乎完全为简谐运动，振幅为8.6°。桁架梁节段模型竖向位移接近简谐运动，并与扭转运动同频，存在轻微的倍频成分。

综合以上分析可知，桁架梁节段模型后颤振表现为弯扭耦合振动特征，并且弯扭耦合程度随着振幅增大而增强。应当指出，在桁架梁节段模型后颤振过程中扭转运动占主导，这不同于薄平板断面和流线型箱梁断面竖向与扭转相互牵连，并且竖向参与度较高的耦合颤振[18-19]。

3.4 极限环振动形态

由3.3节可知，在大幅振动下桁架梁后颤振位移接近简谐运动。因此，桁架梁节段模型极限环振动稳定振幅阶段的竖向与扭转位移可以分别表示为

h(t)=h0sin(2πft+φh0)

(3)

α(t)=α0sin(2πft+φα0)

(4)

式中:h0与α0分别为竖向与扭转振幅；f为振动频率；φh0与φα0分别为竖向与扭转初始相位。

无量纲扭弯幅值比与相位差定义如式(5)、(6)所示

Ramp=(α0/180×π)/(h0/B)

(5)

φαh=φα-φh

(6)

采用正弦函数对桁架梁节段模型稳定振幅阶段竖向与扭转位移分别进行拟合，得到稳定振幅阶段的频率、幅值比与相位差，结果如图9所示。

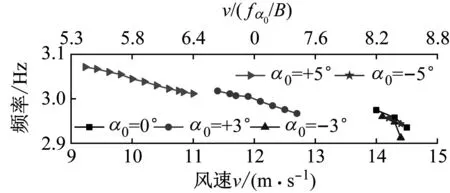
图9 桁架梁节段模型频率、幅值比与相位差随风速变化

由图9可知，在各试验风攻角下，桁架梁节段模型颤振频率均随风速增大(振幅增大)而逐渐减小，这主要与两方面因素有关：其一为桁架梁节段模型结构固有扭转频率随振幅增大而下降，已在2.2节作了详细介绍;其二为气动负刚度增大引起桁架梁节段模型颤振频率下降。

在各试验风攻角下，桁架梁节段模型极限环振动扭弯幅值比均随风速增大(振幅增大)而逐渐减小，表明随着振幅的增大，桁架梁节段模型竖向运动参与程度逐渐增强，该现象与文献中双边肋断面与Π型断面后颤振特征一致。在+5°风攻角下，桁架梁节段模型扭弯幅值比最大，比较接近扭转颤振。在0°与-3°风攻角下，桁架梁节段模型扭弯幅值比较小，表明该风攻角下的弯扭耦合程度相对较大。

在+3°与+5°风攻角下，桁架梁节段模型极限环振动相位差大多在-10°～+3°内。在0°、-3°与-5°风攻角下，桁架梁节段模型极限环振动相位差大多在-24°～-18°内，略大于+3°与+5°风攻角下的相位差。

为进一步分析桁架梁节段模型极限环振动形态，图10给出了+3°风攻角不同风速下桁架梁极限环振动的相平面图。需要说明，该相平面图为根据式(3)、(4)拟合得到的位移，不包括竖向与扭转的静位移以及竖向位移的倍频成分。可以看出，桁架梁节段模型扭转与竖向位移相平面为椭圆形，这也是该类限幅振动称为极限环振动的原因。相平面图中极限环的面积由振幅、相位差综合决定，振幅与相位差越大，极限环面积越大。相平面图也可以说明随着风速增大，桁架梁节段模型极限环振幅显著增大，相位差绝对值总体较小，但随风速增加而轻微增大。该现象不同于文献中双层桥梁桁架梁在+3°与+5°风攻角下弯扭耦合相位差随风速逐渐增大而减小。

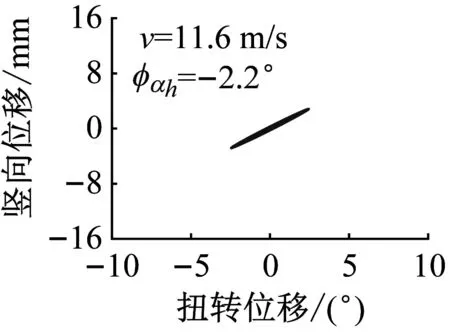
图10 桁架梁节段模型极限环振动相平面图(α0=+3°)

4 极限环振动机理探讨

4.1 极限环振动全过程位移时程

本节对桁架梁节段模型极限环振动过程中的非线性阻尼演变规律进行分析，并对桁架梁节段模型极限环振动机理进行探讨。

在0°、+3°与+5°风攻角下，桁架梁节段模型极限环振动全过程扭转位移时程曲线如图11所示，风速分别为14.5 m/s、12.7 m/s与11.0 m/s。由图11可知，在风速保持不变的条件下，桁架梁节段模型扭转位移增大至一定程度后进入稳定振幅阶段。在0°、+3°与+5°风攻角下，尽管桁架梁节段模型扭转位移均表现为先增长后稳定，但也存在两点差异：其一为桁架梁节段模型在0°风攻角下扭转位移增长较为缓慢，而在+3°与+5°风攻角下扭转位移快速进入稳定振幅状态;其二为在稳定振幅阶段，桁架梁节段模型在0°风攻角下扭转位移峰值存在轻微锯齿状变化，而在+3°与+5°风攻角下扭转位移峰值基本平稳。

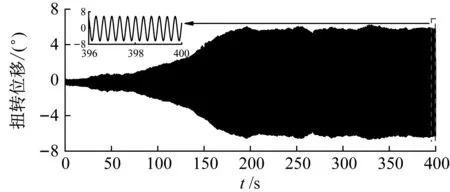
(a) v=14.5 m/s、α0=0°

4.2 非线性阻尼

采用2.1节介绍的分段最小二乘拟合方法识别桁架梁节段模型位移增长过程中的瞬时阻尼比，该阻尼比反映桁架梁节段模型扭转位移增长率，称其为总阻尼比。桁架梁节段模型总阻尼比由结构阻尼比与气动阻尼比两部分组成，如式(7)所示

ξα,total=ξα,aero+ξα,stru

(7)

式中:ξα,total为总阻尼比；ξα,aero为气动阻尼比；ξα,stru为结构阻尼比。

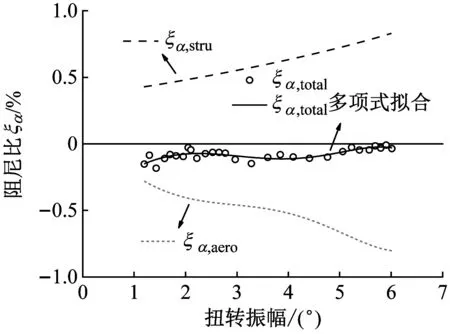
在2.2节已经得到桁架梁节段模型结构阻尼比随振幅变化的关系，根据式(7)可以计算出桁架梁节段模型气动阻尼比随振幅变化的关系，结果如图12所示。

(a) v=14.5 m/s、α0=0°

由图12(a)可以看出，在0°风攻角下，当风速为v=14.5 m/s时，桁架梁节段模型总阻尼比初始值为-0.15%，其绝对值随振幅增大逐渐减为0，进入稳定振幅状态。桁架梁节段模型气动负阻尼的绝对值随振幅增大而增大，意味着非线性气动阻尼不利于振幅稳定，最终桁架梁节段模型出现极限环振动的原因为结构阻尼随振幅的增大而明显增大。

在0°风攻角下，桁架梁节段模型结构阻尼非线性利于颤振稳定，而气动阻尼非线性不利于颤振稳定，两者相互制约。该因素可能是引起桁架梁节段模型极限环振动稳定振幅阶段出现轻微锯齿状波动的原因。

由图12(b)可以看出，在+3°风攻角下，当风速为v=12.7 m/s时，在初始时刻桁架梁节段模型总阻尼比为-0.8%，其绝对值随振幅增大逐渐减为0，进入稳定振幅状态。当振幅小于3°时，桁架梁节段模型气动负阻尼绝对值逐渐减小，利于颤振稳定；当振幅大于3°时，气动负阻尼绝对值缓慢增大，不利于颤振稳定。随着桁架梁节段模型结构阻尼的增大，颤振响应进入稳定振幅状态。

由图12(c)可以看出，在+5°风攻角下，当风速为v=11.0 m/s时，桁架梁节段模型总阻尼比为-0.8%，其绝对值随振幅增大逐渐减为0，进入稳定振幅状态。当振幅大于2°时，桁架梁节段模型气动负阻尼绝对值逐渐减小。此外，桁架梁节段模型结构阻尼随振幅增大而增大，在两者共同作用下，桁架梁节段模型颤振位移最终稳定在某一特定振幅下。

综合以上分析可知，对于弹性悬挂桁架梁节段模型试验，结构阻尼非线性是极限环振动振幅稳定的有利因素，气动阻尼非线性在不同风攻角下具有不同的作用效果。

另外需要说明，桁架梁节段模型颤振位移响应反映出的总阻尼是多方面因素共同作用的综合体现，包括气动力非线性、结构阻尼非线性与结构刚度非线性等。为便于分析，本文从桁架梁节段模型结构阻尼非线性与气动阻尼非线性两方面对极限环振动机理进行探讨，而未考虑刚度非线性等因素对极限环振动的影响。因此，更为精细化的极限环振动机理值得进一步研究。

此外，不同类型桥梁断面的后颤振特性值得比较。钝体主梁断面气动力非线性可引起极限环振动已有较多文献报道，包括双边肋断面、Π型断面等，而平板[20]等流线型断面气动力非线性可能引起颤振剧烈发散，也就是说，不同类型主梁断面的气动力非线性特性显著不同，而且不同试验系统的结构非线性特性也或多或少地存在些许差异，因此不同主梁断面的后颤振自限幅机理不能一概而论，但可以确定结构阻尼非线性对后颤振性能的影响不可轻易忽视。

5 结 论

采用弹性悬挂节段模型风洞试验方法，对桁架梁极限环振动特征与机理进行研究，得到如下主要结论：

(1) 在振幅较大时，弹性悬挂桁架梁节段模型试验系统存在较为明显的阻尼非线性及轻微的刚度非线性，竖向与扭转频率均随振幅增大而减小，竖向与扭转阻尼比均随振幅增大而明显增大。

(2) 在0°、±3°与±5°风攻角下，桁架梁节段模型后颤振现象均表现为极限环振动。在+3°与+5°风攻角下，桁架梁节段模型颤振临界风速较低，振幅随风速增长相对缓慢，在0°、-3°与-5°风攻角下，桁架梁节段模型颤振临界风速较高，振幅随风速增长较为剧烈。

(3) 桁架梁节段模型极限环振动表现为弯扭耦合振动。桁架梁节段模型极限环振动频率、扭弯幅值比随风速增大而减小，表明竖向运动参与程度随风速增大而增强。

(4)对于桁架梁节段模型极限环振动，结构阻尼随振幅增大而增大，是振幅稳定的有利因素。气动阻尼在不同风攻角下具有不同的作用，在0°风攻角下，气动负阻尼绝对值随振幅增大而增大，不利于振幅稳定；在+3°风攻角下，气动负阻尼绝对值随振幅先减小后增大，即初期利于振幅稳定，后期不利于振幅稳定；在+5°风攻角下，气动负阻尼绝对值随振幅增大而减小，利于振幅稳定。